Question

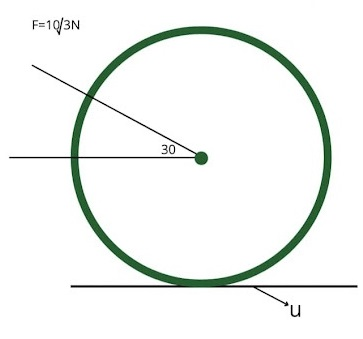
A hollow sphere of mass 2kg is kept on a rough horizontal surface. A force of \[10\sqrt 3 N\]is applied as shown in the figure. Find the minimum value of μ so that the sphere starts pure rolling

A. \[0.3\]
B. \[0.2\]
C. \[0.1\]
D. None of these

Answer 1

Hint:Frictional force is a special type of force which is usually against the direction of motion. In the above problem, the frictional force is between the rough horizontal surface and the hollow sphere. For pure rolling, the rotational and translational acceleration (about the centre of mass of the sphere) should be equivalent. The moment of inertia for rotation of a hollow sphere about its own axis passing through its centre is \[\dfrac{2}{3}M{R^2}\].

Formula Used:
Frictional force,
\[f = \mu Ma\]
where \[\mu \]= coefficient of friction, M = mass of the sphere and a = acceleration
Moment of inertia for rotation of the hollow sphere about its own axis passing through its centre,
\[I = \dfrac{2}{3}M{R^2}\] --- (1)
where R is the radius of the sphere.

Complete step by step solution:
Given: mass of the sphere = 2 kg. Let the force applied be \[F = 10\sqrt 3 N\] and \[\alpha \] be the rotation acceleration and a be the translational acceleration about the centre of mass. N = normal to the surface and g = acceleration due to gravity.
According to the question,
\[F\cos {30^o} - f = Ma\]---- (2)
\[\Rightarrow F\sin {30^o} + Mg = N\]---- (3)
\[\Rightarrow fR = I\alpha \]

So, \[fR = \dfrac{2}{3}M{R^2}\alpha \]
From this we get,
\[f = \dfrac{2}{3}MR\alpha \]---(4)
For pure rolling, \[R\alpha = a\]--- (5)
\[Ma = \dfrac{3}{2}f\]---(6)
The limiting friction will act against the motion of rolling. Thus,
\[f = \mu N\]--- (7)

Substituting (6) and (7) in equation (2), we get,
\[F\cos {30^o} = \dfrac{5}{2}f = \dfrac{5}{2}\mu N\]
\[\mu = \dfrac{{2F\cos {{30}^o}}}{{5N}}\]--- (8)
Substituting value of N from equation (3) in (8),
\[\mu = \dfrac{{2F\cos {{30}^o}}}{{5(F\sin {{30}^o} + Mg)}}\]--- (9)
Applying all values given in question,
\[\mu = \dfrac{{20\sqrt 3 .\sqrt 3 /2}}{{5(10\sqrt 3 .1/2 + 20)}} = 0.1\]
\[\therefore \mu = 0.1\]

Hence option C is the correct answer.

Note: If the force corresponding to translational acceleration is lesser than the force of friction, then the sphere will not move at all. For pure rolling, the rotational acceleration and the acceleration of the centre of mass should have an equivalence of the form \[R\alpha = {a_{CM}}\]. In order that the motion occurs as desired, the two opposing forces should balance out each other.