Question

A gas expands under constant pressure $P$ from volume ${V_1}$​ to ${V_2}$ ​, the work done by the gas is:
A. $P({V_2} - {V_1})$
B. Zero
C. $P({V_1} - {V_2})$
D. $P\left( {\dfrac{{{V_1}{V_2}}}{{{V_2} - {V_1}}}} \right)$

Answer 1

Hint:In the case, when a problem is based on thermodynamics, we know that all the parameters such as pressure, temperature, volume, work done, etc., vary with the given conditions of the system and surroundings hence, use different processes given in thermodynamics to state the answer for the given situation.

Complete step by step solution:
Isobaric process in thermodynamics is a process during which the pressure of a system remains constant that’s why it is also referred to as a constant-pressure process.
$\Delta P = 0$
Since a gas expands under constant pressure $P$ from volume ${V_1}$​ to ${V_2}$ ​, therefore the process is Isobaric.

The Above given can be represented graphically as: -


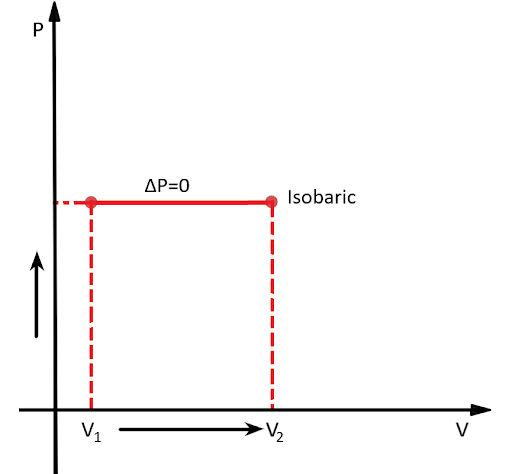
We know that in any thermodynamic process work done is always equal to the area covered by the $P - V$ curve with the volume axis. Therefore, from the above-plotted graph, Pressure-Volume work in thermodynamics is defined as: -
At constant pressure,
$\text{Work done} = W = P\Delta V$
It can also be written as: -
$\text{Work done} = W = P({V_2} - {V_1})$
Thus, when a gas expands under constant pressure, the work done by the gas is $P({V_2} - {V_1})$.

Hence, the correct option is A.

Note: Since this is a problem of multiple-choice question (theory-based) hence, it is essential that given options are analyzed very carefully to give a precise explanation. While writing an explanation of this kind of conceptual problem, always keep in mind to provide the exact reasons in support of your explanation.