Question

A force of \[100N\] is applied on a block of mass \[3kg\] as shown in figure. The coefficient of friction between the surface of the block is\[0.25\] . The friction force acting on acting on the block is:

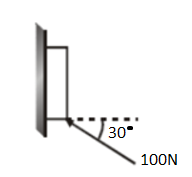
A) \[15N\] downwards
B) \[25N\] upwards
C) \[20N\] downloads
D) \[20N\] upwards

Answer 1

Hint: In this question, we have to first resolve the components of \[F = 100N\]. After resolving the components, we can find the net force on the block. We can find the limiting force between the block and the surface by using the formula ${F_l} = \mu F\cos {30^ \circ }$. After comparing the net force and the limiting force, we can find the friction force acting on the block.

Complete step by step solution:
 According to the question, we have a block of mass \[m = 3kg\]. A force of \[F = 100N\]is applied on the block. Now, resolving the components of the force \[F = 100N\], we get the components according to the following figure.

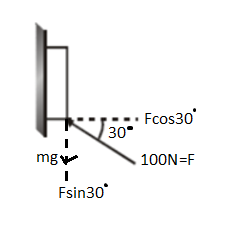
Both components $mg\sin {30^ \circ }$ and $mg\cos {30^ \circ }$ works towards the block. So, $mg\sin {30^ \circ }$works upwards on the block. The weight of the block of $mg$ works downwards on the block. So, net force ${f_a}$ will be given as-
${f_a} = F\sin {30^ \circ } - mg$
Now, substituting the values of force (\[F = 100N\]) , \[sin{30^ \circ } = \dfrac{1}{2}\] , \[m = 3kg\]and \[g = 10\] in the above equation, we get-
\[
  {f_a} = 100 \times \dfrac{1}{2} - 3 \times 10 \\
  {f_a} = 50 - 30 \\
  {f_a} = 20N \\
\]
This net force is directed upwards on the block.
Now, the limiting friction${F_l}$ between the surface and the block will be given as
${F_l} = \mu F$
Substituting the value of \[F = F\cos {30^ \circ }\]and $\mu = 0.25 = \dfrac{1}{4}$ in the above equation, we get-
$
  {F_l} = \mu F\cos {30^ \circ } \\
  {F_l} = \dfrac{1}{4} \times 100 \times \dfrac{{\sqrt 3 }}{2} \\
  {F_l} = 25 \times 0.866 \\
  {F_l} = 21.65N \\
$
The limiting friction is greater than the net force on the block. So, the block will not slip.
So,
${f_r} = {f_a} = 20N$
Hence the friction force acting on the block is equal to \[20N\]and it is directed upwards.

Therefore, option D is correct.

Note: We have to keep in mind that the force is acting towards the block. So, both the components will also be directed towards the block i.e. vertical component is directed upwards. If the limiting friction is greater than the net force then the net force is equal to the friction force acting between the block and surface.