Question

A bolt of mass 0.3 kg falls from the ceiling of an elevator of length 3 m that was going down with a uniform speed of 7 m/s. It hits the elevator floor without a rebound. Find the heat produced by its impact. If the elevator was stationary, would there be a change in the heat produced?

Answer 1

Hint: The heat produced on impact will be the loss in its mechanical energy. The mechanical energy of the bolt is the sum of its kinetic energy and its potential energy. In the case of the moving elevator, we consider the relative velocity of the bolt. No rebound suggests that the final velocity of the bolt is zero.

Formula Used:
1. The relative velocity of an object A is given by, ${v_{rel}} = {v_A} - {v_f}$ where ${v_A}$ is the exact velocity of A and ${v_f}$ is the velocity of the frame of reference.
2. The heat produced is given by, $H = \Delta E$ where $\Delta E$ is the change in mechanical energy.
3. The potential energy of the bolt is given by, $U = mgh$ where $m$ is the mass of the object, $g = 9.8{\text{m/}}{{\text{s}}^2}$ is the acceleration due to gravity and $h$ is the height at which the object is raised.

Complete step by step answer:
Step 1: Sketch a diagram of the problem at hand and list the known parameters.
Bolt falls down from the top of the elevator to the floor.
                
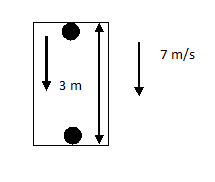
The mass of the bolt is $m = 0.3{\text{kg}}$ .
The velocity of the elevator is ${v_e} = 7{\text{m/s}}$ .
The length of the elevator constitutes the height from which the bolt falls down, $h = 3{\text{m}}$ .
Step 2: Find the heat produced when the elevator is moving with a uniform speed.
As the bolt falls from a moving elevator its relative initial velocity will be zero.
Let ${u_{rel}} = 0$ be the relative initial velocity of the bolt and ${u_b}$ be the exact initial velocity of the bolt.
The relative velocity of an object A is given by, ${v_{rel}} = {v_A} - {v_f}$ where ${v_A}$ is the exact velocity of A and ${v_f}$ is the velocity of the frame of reference.
Then the relative initial velocity of the bolt will be ${u_{rel}} = {u_b} - {v_e}$
Substituting for ${u_{rel}} = 0$ and ${v_e} = 7{\text{m/s}}$ in the above equation we get, ${u_b} = 7{\text{m/s}}$ .
Thus the exact initial velocity of the bolt is 7 m/s.
Since there is no rebound, the relative final velocity of the bolt will also be zero.
 Let ${v_{rel}} = 0$ be the relative final velocity of the bolt and ${v_b}$ be the exact final velocity of the bolt.
Then the relative final velocity of the bolt will be ${v_{rel}} = {v_b} - {v_e}$
Substituting for ${v_{rel}} = 0$ and ${v_e} = 7{\text{m/s}}$ in the above equation we get, ${v_b} = 7{\text{m/s}}$ .
Thus the exact final velocity of the bolt is also 7 m/s. So, the velocity of the bolt during the fall is uniform. This implies that there is no change in the kinetic energy of the bolt i.e., $\Delta K = 0$ .
The potential energy of the bolt is given by, $U = mgh$
Substituting the values for $m = 0.3{\text{kg}}$ , $g = 9.8{\text{m/}}{{\text{s}}^2}$ and $h = 3{\text{m}}$ in the above equation we get, $U = 0.3 \times 9.8 \times 3 = 8.82{\text{J}}$ .
The potential energy of the bolt changes as the bolt moves along the length of the elevator and it is $\Delta U = 8.82{\text{J}}$ .
Now the heat produced is given by, $H = \Delta E = \Delta \left( {K + U} \right)$ as the mechanical energy $E$ is the sum of the kinetic energy $K$ and potential energy $U$ .
Here since the change in kinetic energy is zero, $H = \Delta U = 8.82{\text{J}}$ .
Therefore, the heat produced on impact when the elevator is moving is $H = 8.82{\text{J}}$ .
Step 4: Find the heat produced when the elevator is stationary.
Now the bolt falls from the top of a stationary elevator and has no rebound as it touches the elevator floor.
Thus the initial velocity of the bolt is ${u_b} = 0{\text{m/s}}$ and the final velocity of the bolt is ${v_b} = 0{\text{m/s}}$ .
Thus, the velocity of the bolt during the fall is uniform. This implies that there is no change in the kinetic energy of the bolt i.e., $\Delta K = 0$ .
The change in the potential energy of the bolt will be the same as that in the first case i.e., $\Delta U = 8.82{\text{J}}$.
Therefore, the heat produced on impact will also be the same as $H = 8.82{\text{J}}$ .

Note: Here, the falling of the bolt happens inside the elevator. Thus the elevator is set to be the frame of reference in which the bolt falls down. Also, when the bolt is falling down as the elevator is moving downwards, both the bolt and the elevator will be moving in the same direction. Also the heat produced won’t be any different even if the elevator was stationary, as the kinetic energy of the bolt due to the elevator is anyways not affecting the heat, only the potential energy of the bolt is getting converted into heat.