Question

A body B lies on a smooth horizontal table and another body A is placed on B. The coefficient of friction between A and B is μ. What acceleration given to B will cause slipping to occur between A and B.
A. \[\mu g\]
B. $\dfrac{g}{\mu }$
C. $\dfrac{\mu }{g}$
D. $\sqrt {\mu g} $

Answer 1

Hint:
friction is a force that resists the sliding of two surfaces against each other. The frictional force is proportional to the normal force, which is the force that is perpendicular to the surfaces. The coefficient of friction, $\mu $, determines how much friction there is between the two surfaces. We can define friction as $f = \mu N$ where N is the normal. Draw the free body diagram of the system and for body A.




Complete step by step solution:

Here first draw picture of the scenario

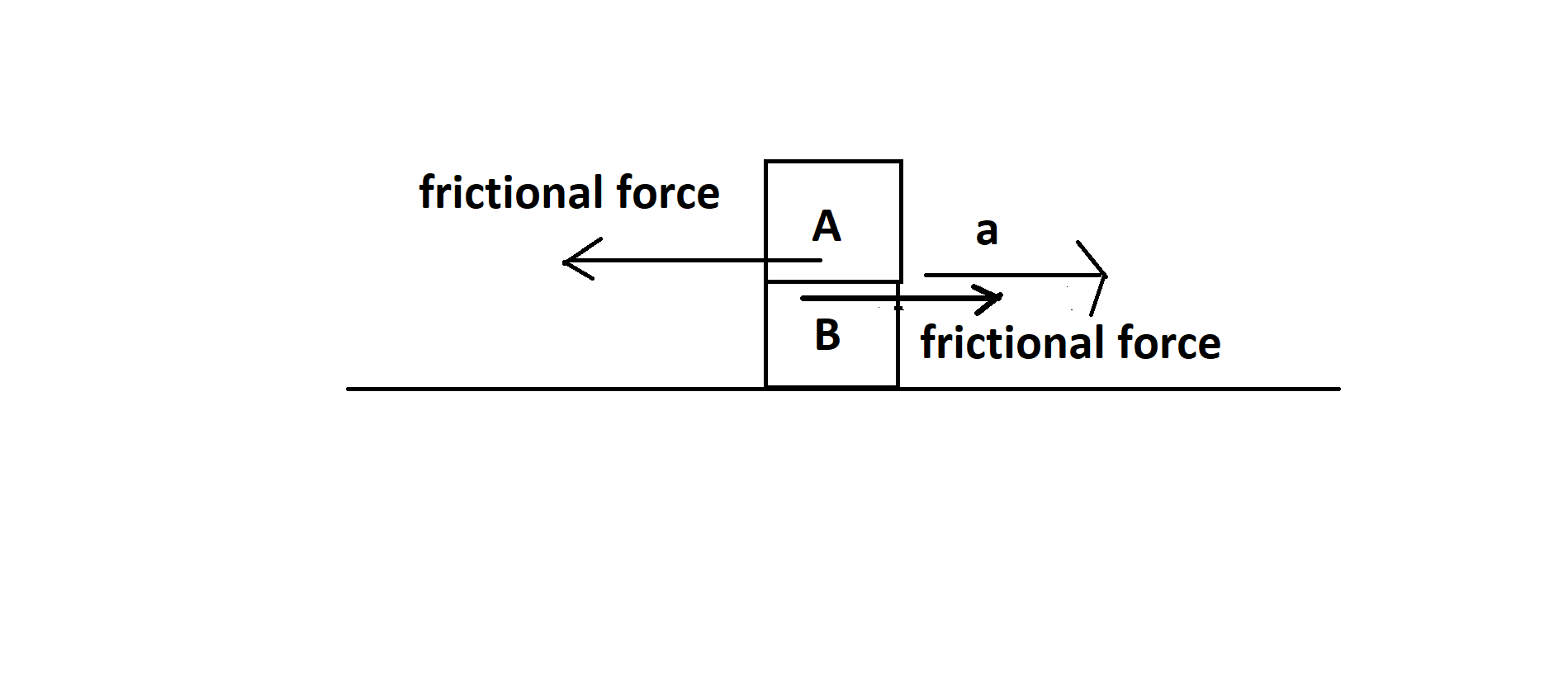
Here we consider that the whole system is given an acceleration a. The surface is smooth so that there is no friction between the body B and the surface. The frictional force is proportional to the normal force, which is the force that is perpendicular to the surfaces. The coefficient of friction, $\mu $, determines how much friction there is between the two surfaces. We can define friction as $f = \mu N$ where N is the normal. Now if we look at the picture, we see that there is a friction between the surfaces of A and B. As the system is moving forward then frictional force of body A in backward direction. Now do another diagram for body A.

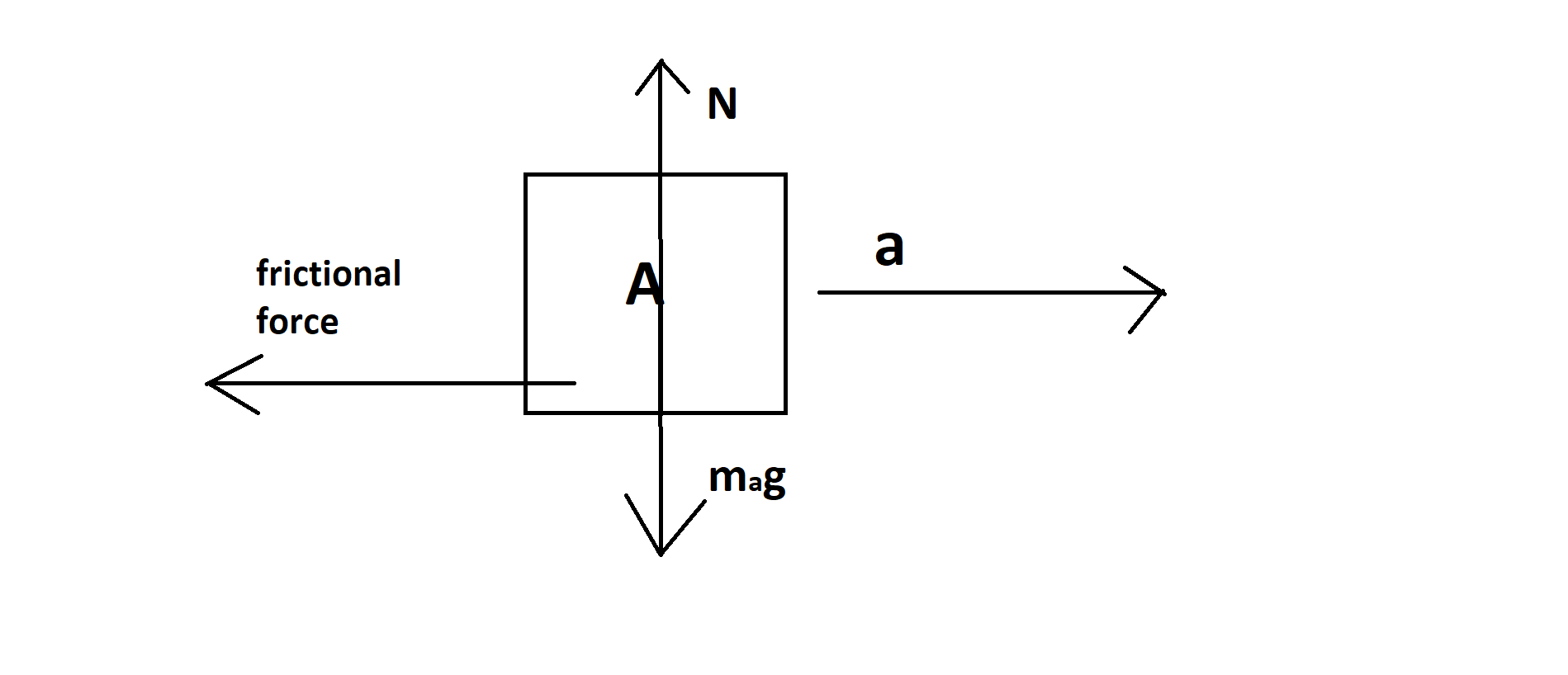
Now we have to think about the condition of slipping of body A. When frictional force is less than equal to applied force then it will start slipping. So, let's equate this. If we acceleration of the system is a then force on the forward direction is given by \[F = ({m_a} + {m_b})a\] here ${m_a},{m_b}{\text{ is the mass of body A and B}}{\text{.}}$ we already told you that frictional force is equal to $f = \mu N$ so we can write here that $f = \mu {m_a}g$ . So now we can write ${m_a}a = \mu {m_a}g$.Actually here we are considering a pseudo force ${m_a}g$. Also, we can write $a = \mu g$. Hence option A is the correct option.

Therefore, option (A) is the correct option.



Note:
Frictional is a force which opposes the relative motion between two bodies. Mathematically expressed as $f = \mu N$ . A body lies on another body which is lying on a smooth surface then they will be sliding when acceleration of the system is equal to the product of coefficient of friction between the bodies and gravitational acceleration.