




How Do the Triangle Law and Parallelogram Law Work in Vector Addition?
Understanding the Triangle Law And Parallelogram Law is essential for JEE aspirants mastering vector addition in Physics. At Vedantu, we introduce these laws for clear exam preparation and conceptual depth.
What Are Vectors?
A vector is a quantity with both magnitude and direction, often represented as an arrow. Position, force, and velocity are common examples. Unlike scalars, vectors require geometric methods when being added, since their direction matters.
In problems involving displacement or force, you’ll find vectors must be added by methods such as the triangle law and parallelogram law, not by simple arithmetic. This ensures their directional properties are respected in calculations.
Triangle Law of Vector Addition
The triangle law of vector addition states: If two vectors are represented in magnitude and direction by two sides of a triangle drawn in sequence, then the third side represents the sum. This method is key for combining two vectors where direction is pivotal.
Suppose you have vectors D and E. Place the tail of E at the head of D. The vector from the tail of D to the head of E is the resultant.
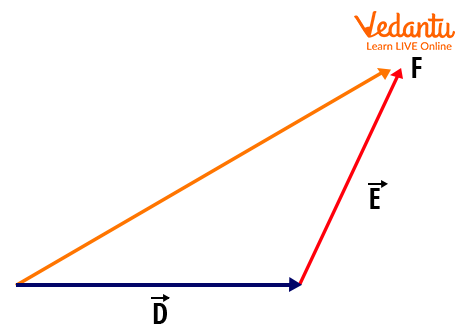
The formula for the magnitude of the resultant vector using the triangle rule and parallelogram law is:
- $|R| = \sqrt{d^2 + e^2 + 2de \cos\theta}$
Here, d and e are the magnitudes of the vectors, and θ is the angle between them. This triangle law and parallelogram law of vector addition formula is crucial for JEE problems and appears often in Class 11 Physics.
If you want to find the angle φ between the resultant vector and vector D, the triangle law and parallelogram law derivation gives us:
- $\tan \phi = \dfrac{e \sin\theta}{d + e \cos\theta}$
Parallelogram Law of Vector Addition
The parallelogram law of vector addition states: If two vectors are acting at a single point and are represented by adjacent sides of a parallelogram, then their resultant is represented by the diagonal from that point. This law is a foundation for handling forces and motions in two directions simultaneously.
For vectors D and E, arranged as adjacent sides, the diagonal represents their sum. The parallelogram law and triangle rule are fundamentally equivalent but used in varying geometric scenarios.
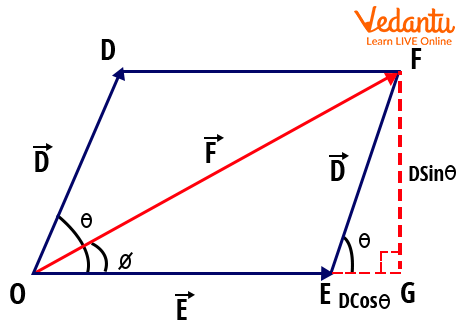
The resultant’s magnitude by the parallelogram law is also:
- $|R| = \sqrt{D^2 + E^2 + 2DE \cos\theta}$
The angle between the resultant and E is given by:
- $\tan \phi = \dfrac{D \sin\theta}{E + D \cos\theta}$
Application and Geometric Interpretation
In JEE Physics, the triangle law and parallelogram law of vector addition class 11 syllabus covers these concepts for kinematics, force, and motion topics. Visualization helps in understanding the resultant direction and magnitude clearly.
Parallelogram and triangle law are also used to analyze position vectors and displacements, linking with systems in position vector and displacement and kinematics problems.
Mathematical Derivation: Parallelogram Law
Suppose two vectors D and E act at a point with an angle θ between them. The resultant diagonal can be found using the law of cosines:
- By geometry, the diagonal’s length is $R^2 = D^2 + E^2 + 2DE\cos\theta$
This formula is central in physics when forces combine at a point, like in statics or mechanics. The parallelogram construction shows how both direction and magnitude are essential in combining vectors accurately.
Triangle Law and Parallelogram Law: Difference
While both laws describe vector addition, their geometrical approaches differ. The triangle law uses successive sides of a triangle, while the parallelogram law works from a single origin, forming a parallelogram. However, both yield the same result mathematically.
| Triangle Law | Parallelogram Law |
|---|---|
| Connects vectors head-to-tail | Shares origin as adjacent sides |
| Forms a triangle | Forms a parallelogram |
| Resultant is third side | Resultant is diagonal |
How Triangle and Parallelogram Laws Are Used
These laws are used to add forces, velocities, or displacements—any situation where vectors must be combined. The triangle rule is especially useful in sequential movements, while the parallelogram law simplifies force analysis at a common point.
For example, in torque and rotational motion, vector addition helps analyze combined effects, while the same principle supports angular momentum of rotating body analysis.
Solved Numerical Examples
Consider two vectors of magnitudes 3 units and 4 units with a 60° angle between them. Using the triangle law and parallelogram law formula, the resultant is $|R| = \sqrt{3^2 + 4^2 + 2 \times 3 \times 4 \cos 60^\circ} = \sqrt{9 + 16 + 24 \times 0.5} = \sqrt{37} = \mathbf{6.08}$ units.
Another scenario: if vectors have magnitudes 5 units and 7 units, and the angle between them is 30°, the angle between the resultant vector and the second vector is given by $\tan \phi = \frac{5 \sin 30^\circ}{7 + 5 \cos 30^\circ} = \frac{5 \times 0.5}{7 + 5 \times 0.866} = \frac{2.5}{11.33} \Rightarrow \phi = \mathbf{12.5}^\circ$.
Connections with Other Physics Concepts
The triangle rule and parallelogram law are the backbone of vector techniques throughout JEE Physics. They also appear in topics like dynamics of rotational motion and center of mass.
Mastery of triangle law and parallelogram law of vector addition class 11 content forms a solid foundation for both modern physics and real-world applications in mechanics, making these concepts vital in both exams and practical engineering contexts.
FAQs on Understanding the Triangle Law and Parallelogram Law
1. What is the Triangle Law of Vector Addition?
The Triangle Law of Vector Addition states that if two vectors are represented as two sides of a triangle taken in order, their sum is given by the third side taken in the opposite order.
Key points include:
- Place the tail of the second vector at the head of the first vector.
- The resultant vector is drawn from the tail of the first to the head of the second vector.
- This law visually represents the sum of two vectors, commonly used in physics and mathematics.
2. How does the Parallelogram Law of Vector Addition work?
The Parallelogram Law of Vector Addition states that if two vectors are represented by adjacent sides of a parallelogram, both starting at the same point, their resultant is given by the diagonal passing through that point.
Main steps:
- Draw both vectors from the same point.
- Complete the parallelogram using both vectors.
- The diagonal from the common point shows the resultant vector.
- This law helps in analytically and graphically finding vector sums.
3. What is the main difference between the Triangle Law and Parallelogram Law of vector addition?
The main difference lies in representation, but both yield the same resultant vector.
- Triangle Law: Vectors are placed one after another (head-to-tail).
- Parallelogram Law: Both vectors start from a common point and the resultant is the diagonal.
- Both laws are equivalent and used based on convenience.
4. How do you find the magnitude and direction of the resultant using the Parallelogram Law?
The magnitude and direction of the resultant vector can be found using the parallelogram law formula.
- If two vectors a and b make an angle θ,
- Resultant’s magnitude, R = √(a² + b² + 2ab cosθ)
- Direction, tanα = (b sinθ) / (a + b cosθ)
- Here, α is the angle the resultant makes with vector a.
5. Why are the Triangle Law and Parallelogram Law of vector addition important?
These laws are important because they help solve problems involving multiple forces or velocities.
- They provide graphical and analytical techniques for vector addition.
- Used extensively in physics, engineering, and mathematics.
- Essential for understanding resultant forces, displacements, and velocities.
6. Can you explain Vector Addition using a simple example?
Yes, for example, if two vectors of 3 units and 4 units are at right angles, applying the triangle law gives:
- Form a right triangle with sides 3 and 4 units.
- Resultant = √(3² + 4²) = 5 units (Pythagoras theorem).
- The direction is found using tangent inverse: tanθ = 4/3.
7. State the Triangle Law of vector addition.
The Triangle Law of Vector Addition states: If two vectors are represented in magnitude and direction by two sides of a triangle taken in the same order, then their resultant is represented by the third side of the triangle taken in the opposite order.
- This is applicable for adding two vectors graphically.
- Helps in solving vector-related problems in science and engineering.
8. What is the parallelogram law of vectors? State its statement.
The Parallelogram Law of Vectors states: If two vectors are acting simultaneously at a point and are represented in magnitude and direction by the two adjacent sides of a parallelogram, then their resultant is represented in magnitude and direction by the diagonal passing through that point.
- Commonly used in force and physics calculations.
9. Where is vector addition used in daily life?
Vector addition is used in many real-life scenarios such as:
- Determining resultant force when many forces act on an object.
- Calculating net displacement or velocity.
- Navigation for airplanes and ships using two velocities (current/wind + own speed).
- Combining movements in sports and physics experiments.
10. How are the Triangle Law and Parallelogram Law related?
The Triangle Law and Parallelogram Law are equivalent methods for vector addition.
- Both derive the same resultant vector for two vectors.
- The triangle law is a special case of the parallelogram law where the vectors are joined head to tail.
- Choice of method depends on problem convenience.


















