




Quadratic Equations are a very fundamental topic in Mathematics. In daily life we use quadratic formulas for calculating areas, determining a product's profit, or formulating the speed of an object. Now, let us first know what a quadratic equation is.
Quadratic Equations Roots in Detail
All the equations of the form $ax^2+bx+c=0$ ($a \neq 0$ & $a,~b,~c \in \mathbb{C}$) are quadratic equations, where, a, b, c are coefficient of $x^2, x$ and the constant term. As it has power 2, it will have two roots. In this part, we will calculate roots by various methods and try to generalize formulas that will be useful in JEE.
What are the Roots of Quadratic Equations?
Suppose we have a quadratic polynomial $f(x)=ax^2+bx+c$ ($a \neq 0; a,~b,~c\in \mathbb{C}$), Now roots are all the points $x=\alpha\in\mathbb{C}$ such that, $f(\alpha)=0$. For a quadratic equation, the number of roots is at most 2. If we look carefully, f(x) is an equation of a parabola. Basically for real roots, roots are all those points where the parabola intersects the x-axis. If the parabola does not intersect the x-axis then no roots are complex. For the x-axis being the tangent of the parabola, the roots are the same.
Finding Roots of Quadratic Equation
Here, we will discuss a few techniques to solve quadratic equations.
By Factorisation
Suppose, $ax^2+bx+c=0$ is a quadratic equation. Now, we will try to find two function $f(x)=x-\alpha$ & $g(x)=x-\beta$ such that, $ax^2+bx+c=f(x)g(x)=(x-\alpha)(x-\beta)=0$
Then, $x=\alpha$ & $x=\beta$ will be the roots of the quadratic equation. We discuss factorization with an example below.
Let, our quadratic equation is $x^2-5x+6=0$, now we will try to find a $\alpha$ such that $\alpha^2-5\alpha+6=0$. See, it holds true if $\alpha=2$
So, (x-2) is a factor of that quadratic equation, now we need to find another one. Now, we divide $x^2-5x+6=0$ by (x-2) to get the other factor.
$\dfrac{x^2-5x+6}{x-2}=\dfrac{x^2-2x-3x+6}{x-2}=x-3$
So, we get, x=2, x=3 are the roots of the equations.
But there are certain drawbacks of this technique, if the roots are imaginary or irrational it’s hard to guess one $\alpha$ for the equation.
By Quadratic Equation’s Root Formula
First developed by Indian Mathematician Shreedhar Acharya, It is the most efficient way of finding the roots. We will just calculate the formula and it is very essential you memorize it properly.
So, we have our quadratic equation, $ax^2+bx+c=0$
$\begin{align} &a x^{2}+b x+c=0 \\ &\Rightarrow x^{2}+\dfrac{b}{a} x+\dfrac{c}{a}=0 \\ &\Rightarrow x^{2}+2 \times x \times \dfrac{b}{2 a}+\dfrac{b^{2}}{4 a^{2}}-\dfrac{b^{2}}{4 a^{2}}+\dfrac{c}{a}=0 \\ &\Rightarrow\left(x+\dfrac{b}{2 a}\right)^{2}=\dfrac{b^{2}-4 a c}{4 a^{2}} \\ &\Rightarrow\left(x+\dfrac{b}{2 a}\right)=\pm \dfrac{\sqrt{b^{2}-4 a c}}{2 a} \\ &\Rightarrow x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a} \end{align}$
This is the quadratic formula to find roots.
By Completing Square
Just like the previous method, we have,
$a x^{2}+b x+c=a\left(x+\dfrac{b}{2 a}\right)^{2}-\dfrac{b^{2}-4 a c}{4 a}$
We can make the equation like this and calculate it to find the roots.
Nature of Roots of Quadratic Equations
We have the roots of the quadratic equation, $ax^2+bx+c=0$ as
$\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}$
Now, say this part $b^2-4ac$ as “Discriminant” and define it by D
So, $D=b^2-4ac$
now, we can check the nature of roots depending on the discriminant
Let’s say D=0 , then the roots are the same,
i.e $x=\dfrac{-b}{2a}$
For D > 0, then the nature will not only be real but will also be distinct, i.e. $\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}$
For D < 0, then the nature will be non-real or imaginary or complex roots, i.e $\dfrac{-b \pm i \sqrt{4 a c-b^{2}}}{2 a}$
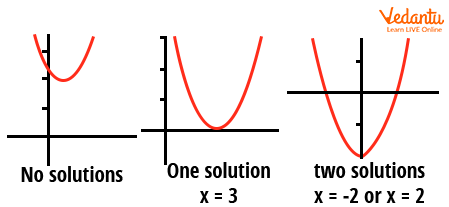
Nature of Roots of Quadratic Equation
Properties of Roots
Now, we have the formula of finding the roots of a quadratic equation $ax^2+bx+c=0$, let $\alpha,~\beta$ are the roots of the equation
Then, $\alpha=\dfrac{-b+\sqrt{b^{2}-4 a c}}{2 a}$ & $\beta=\dfrac{-b-\sqrt{b^{2}-4 a c}}{2 a}$
Now see, $\alpha +\beta=\dfrac{-b}{a}$ and $\alpha\beta=\dfrac{c}{a}$
So, we get for a quadratic equation ax2+bx+c=0, the sum of roots of quadratic equation is $-\dfrac{b}{a}$ and the product of roots of quadratic equation is $\dfrac{c}{a}$.
So a quadratic equation can be written as
$x^2-(\alpha+\beta)x+\alpha\beta=0$,
This is the quadratic formula.
Geometric Approach of Understanding Root of Quadratic Equation
Consider the equation of Parabola $y=ax^2+bx+c$, by the root of this equation we mean where the x-axis cuts the graph of this parabola, that is where, y=0. Consider the parabola $y=x^2-4$.We can tell that it has roots at $x=\pm2$, and in the diagram, we can also see that it intersects the x-axis at two points,i.e. $x=\pm2$. This is another way of finding out roots. If the parabola just touches the x-axis at one point, the roots are the same and in that case, we can check D=0. Again if the parabola does not intersect the x-axis at any point, the equation has no real root and in that case, we can check D<0. This is the geometric approach in understanding the roots of Quadratic equations.
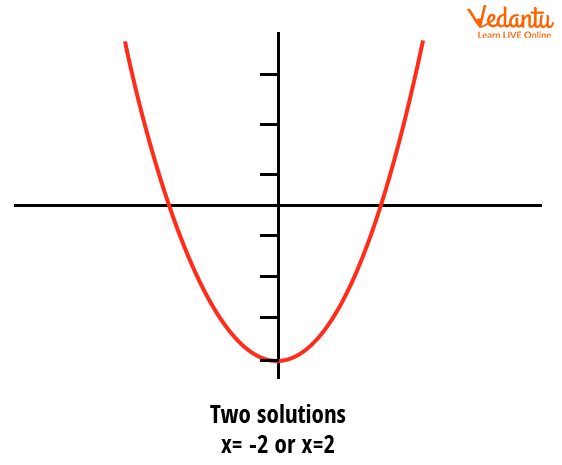
Geometric Approach of Understanding Root of Quadratic Equation
We’ll now look at the roots of quadratic equation examples.
Some Examples of Quadratic Equations for JEE
Example1: For what real values of p
$\left(p^{2}-16\right) x^{2}-\left(4+4 p+p^{2}\right) x-p^{3}-4 p^{2}-4 p-16=0$
have more than two solutions?
Solution:
As it is a quadratic equation and it is said to have more than two roots, hence it will be one identity, so
$p^{2}-16=4+5 p+p^{2}=-p^{3}-4 p^{2}-4 p-16=0$
So,
$\begin{align} &p^{2}-16=0 \\ &\Rightarrow p=\pm 4 \\ &4+5 p+p^{2}=0 \\ &\Rightarrow p=-4,-1 \\ &-p^{3}-4 p^{2}-4 p-16=0 \\ &\Rightarrow p=-4 \end{align}$
So, the answer is p=-4.
2. Example: If both the roots of the quadratic equation x2-mx+4=0 are real and distinct, then find the range of m.
Solution: So, roots are real and distinct, then
$\begin{align} &m^{2}-4 \times 4 \times 1<0 \\ &\Rightarrow m^{2}<16 \\ &\Rightarrow-4<m<4 \end{align}$
So, $m \in(-4,4)$
Conclusion
Here we have tried to discuss the Quadratic equation, both algebraically and geometrically. Both will be useful in solving problems faster and efficiently. The formulas for the sum and product of roots are very useful and handy and to be memorized. This is a prior concept to solving equations with a power of more than 2 and it will be a lot easier to generalize from this. Quadratic equation is a very important chapter in JEE Main. Not only is there good weightage, but also good knowledge can help you get answers fast and efficiently. We recommend you to solve problems with complex numbers because they are important in JEE exams.
FAQs on Quadratic Equations Roots in Detail for JEE
1. What are the applications of quadratic equations?
Quadratic Equations are useful tools in getting solutions to many questions easily. It is a polynomial equation with a maximum degree of 2. It is a very fundamental concept that one should know. It has some good real-world implications for every two variable systems in nature.
oreover, you will find applications in solving differential equations, and integration and it also gives a good approach in understanding the geometry of parabola, which is a frequent topic in Physics and you will get applications in Chemistry too, while solving physical chemistry.
2. What is the weightage of quadratic equations in JEE?
As I mentioned earlier it is an important tool to solve problems but each year JEE tends to give one or two questions in the exam, mainly with complex roots or concepts using range and all that. It can happen that you may not find any direct questions in JEE, But it is a very fundamental and equally important concept that will help you solve other problems in JEE and I can assure you that you have to solve Quadratic Equations at least once, be that direct question or part of the solution.
























