




How to Solve Projectile Motion Problems on an Inclined Surface
Projectile motion on an inclined plane studies the path of an object projected with an initial velocity at a certain angle to the horizontal, but where the landing surface is a slope instead of a flat ground. The analysis requires resolving the velocity, applying kinematic equations, and modifying range and time formulas to account for the angle of inclination.
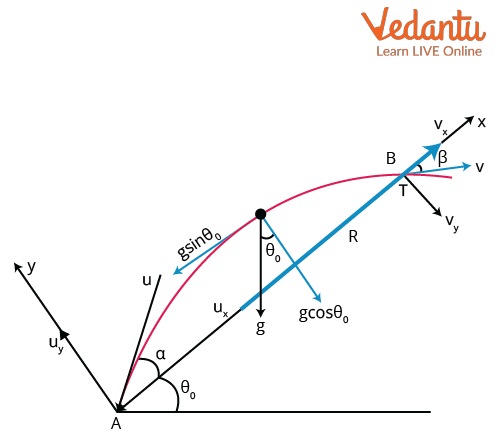
Key Parameters in Projectile Motion on an Inclined Plane
In projectile motion on an inclined plane, the initial velocity is denoted by $u$, the angle of projection with the horizontal is $\theta$, and the inclination angle of the slope with the horizontal is $\alpha$. The acceleration due to gravity is represented by $g$. These parameters influence all major equations for analysis.
For a comprehensive understanding of two-dimensional motion concepts supporting this topic, see the section on Motion In 2D Dimensions.
Standard Formulas for Projectile on an Inclined Surface
For accurate analysis of projectile motion on an inclined plane, three key equations are applied: range along the slope, time of flight before landing on the slope, and maximum height achieved relative to the horizontal axis. All depend on both the projection angle $\theta$ and plane inclination $\alpha$.
| Quantity | Formula (Inclined Plane) |
|---|---|
| Range (R) | $\dfrac{2u^2 \cos\theta \sin(\theta-\alpha)}{g\cos^2\alpha}$ |
| Time of Flight (T) | $\dfrac{2u \sin(\theta-\alpha)}{g\cos\alpha}$ |
| Maximum Height (H) | $\dfrac{u^2 \sin^2\theta}{2g\cos^2\alpha}$ |
Notice the adjustment of these formulas compared to standard horizontal projectile motion, reflecting the transformation required by the slope. The direction and sign of $(\theta-\alpha)$ must always be handled with care.
Derivation for the Range on an Inclined Plane
To derive the range formula for a projectile on an inclined plane, begin by resolving the initial velocity $u$ into horizontal and vertical components. The horizontal component is $u\cos\theta$ and the vertical component is $u\sin\theta$. The positions in time $t$ are given by $x = u\cos\theta\, t$ and $y = u\sin\theta\, t - \dfrac{1}{2}gt^2$ with $x$ and $y$ measured from the base of the slope.
The condition for the projectile to strike the incline is $y = x\tan\alpha$, which ensures the projectile's position aligns with the slope at the instant of landing. Substituting and simplifying:
$u\sin\theta\, t - \dfrac{1}{2}gt^2 = u\cos\theta\, t \tan\alpha$
Rearranging and solving for $t$ (ignoring $t=0$),
$t = \dfrac{2u(\sin\theta - \cos\theta \tan\alpha)}{g}$
This simplifies to the time of flight:
$T = \dfrac{2u \sin(\theta-\alpha)}{g\cos\alpha}$
Substituting $T$ into $x = u\cos\theta\, t$, the range along the slope is found as:
$R = \dfrac{2u^2 \cos\theta \sin(\theta-\alpha)}{g\cos^2\alpha}$
A detailed explanation of kinematics underpinning this derivation is available in Understanding Kinematics.
Comparison: Inclined Plane versus Horizontal Surface
Projectile motion on a horizontal surface uses the formulas $R = \dfrac{u^2 \sin 2\theta}{g}$ and $T = \dfrac{2u\sin\theta}{g}$. On an inclined plane, gravity's orientation relative to the surface changes the effective range and time of flight, resulting in the more complex equations shown above. The path is no longer symmetric due to the incline.
For clarity on the distinction between these scenarios, refer to Projectile Motion Explained.
Practical Example: Calculation on an Inclined Plane
Consider a particle projected with speed $u = 20$ m/s at $\theta = 40^\circ$ above the horizontal onto an incline with $\alpha = 20^\circ$. Find the range $R$ (using $g=10$ m/s$^2$).
- $R = \dfrac{2u^2 \cos\theta \sin(\theta-\alpha)}{g\cos^2\alpha}$
- Substitute: $u=20$, $\theta=40^\circ$, $\alpha=20^\circ$, $g=10$
- Calculate $\cos\theta = \cos 40^\circ \approx 0.766$, $\cos\alpha = \cos 20^\circ \approx 0.940$
- Compute $\sin(\theta-\alpha) = \sin 20^\circ \approx 0.342$
- $R = \dfrac{2 \times 400 \times 0.766 \times 0.342}{10 \times 0.884}$
- $R \approx \dfrac{209.3}{8.84} \approx 23.7$ m
This method can be applied to diverse exam questions, and stepwise calculations help prevent errors. To practice more problems, see Kinematics Important Questions.

Common Errors in Inclined Plane Projectile Problems
Solving projectile motion on an inclined plane for exams often leads to mistakes involving angle confusion, application of standard horizontal formulas, or incorrect decomposition of initial velocity. Applying correct trigonometric relationships and sign conventions is crucial for accuracy.
- Do not interchange $\theta$ and $\alpha$
- Use velocity components parallel and perpendicular to the slope
- Include $\cos^2\alpha$ in denominators as required
- Correctly use $\sin(\theta-\alpha)$ for direction
To test conceptual strength and avoid pitfalls, undertake targeted practice using Kinematics Mock Test resources.
Effect of Inclination Angle on Projectile Range
The inclination angle $\alpha$ significantly affects the displacement along the slope. A larger slope angle decreases the range for the same initial velocity and projection angle. When $\theta = \alpha$, the projectile lands immediately at the projection point, as $\sin(\theta-\alpha)=0$.
Optimizing range on an incline requires selecting the correct projection angle relative to the slope. For in-depth discussions on maximizing displacement in such cases, reference Motion Of Satellites Explained for advanced analogies and conceptual links.
Applications and Problem-Solving in Examinations
Projectile motion on inclined planes appears often in engineering, sports on hills, and advanced physics problems. Exam questions target all special cases, including projections up and down the slope, and ensure mastery of formula variations.
- Analyze diagrams before applying formulas
- Down-the-incline projection: measure $\theta$ below horizontal
- Review angle conventions for each configuration
- Solve a diverse set of numerical examples
To deepen your understanding with more solved problems, structured notes, and thorough explanations, refer to Understanding Kinematics.
FAQs on Understanding Projectile Motion on an Inclined Plane
1. What is projectile motion on an inclined plane?
Projectile motion on an inclined plane refers to the path traced by an object launched at an angle to the horizontal, where the landing surface itself is inclined. Key points:
- The projectile follows a parabolic trajectory relative to the inclined plane.
- Motions are analyzed by resolving the velocity and acceleration into components parallel and perpendicular to the incline.
- This concept is commonly tested in CBSE Physics syllabus for competitive and board exams.
2. How do you calculate the range of a projectile on an inclined plane?
The range of a projectile on an inclined plane is determined using special formulas:
- Let θ = angle of projection relative to ground.
- α = angle of inclination of the plane.
- u = initial velocity.
- The range (R) along the plane:
R = (2u2 cosθ sin(θ - α))/[g cos2α]
3. What is the formula for time of flight on an inclined plane?
Time of flight on an inclined plane is the total time the projectile remains in air before landing on the slope:
- For a projectile fired with velocity u at angle θ to the horizontal, onto a plane inclined at angle α:
- Time of flight, T = (2u sin(θ - α))/(g cosα)
4. What are the key differences between projectile motion on a horizontal and on an inclined plane?
The differences between projectile motion on a horizontal and inclined plane are:
- On a horizontal plane, standard formulas for range and time apply.
- On an inclined plane, velocity and gravity are resolved along and perpendicular to the plane.
- Formulas include adjustments for the angle of inclination (α).
- The range and maximum height are relative to the inclined surface, not the ground.
5. How do you resolve the velocity components in projectile motion on an inclined plane?
Resolving velocity components on an inclined plane involves:
- Splitting the initial velocity (u) into two parts:
- Along the plane: uparallel = u cos(θ - α)
- Perpendicular to the plane: uperpendicular = u sin(θ - α)
- This method simplifies analysis and helps derive correct expressions for range and time of flight in CBSE-type questions.
6. What is the condition for maximum range of a projectile on an inclined plane?
The condition for maximum range on an inclined plane is:
- Maximum range occurs when θ = (45° + α/2), where θ is angle of projection and α is the inclination.
- This ensures the projectile covers the farthest distance along the slope.
- This is a frequent concept in CBSE and entrance exams.
7. Why does the range change when the projectile is launched on an inclined plane instead of a flat surface?
The range changes because the direction of the landing surface affects the gravitational components acting on the projectile:
- An inclined plane creates different effective acceleration and travel distance along the slope.
- The angle of inclination alters how far the projectile can go before hitting the surface.
8. How does the angle of projection affect projectile motion on an inclined plane?
The angle of projection (θ) affects both the time of flight and range:
- A larger angle generally increases height but may decrease range for steep inclines.
- For maximum range along the incline, the angle should be θ = 45° + (α/2).
- Part of the syllabus covers finding the best angle for maximum distance covered.
9. What assumptions are made in the study of projectile motion on an inclined plane?
Common assumptions in projectile motion problems on an inclined plane include:
- Negligible air resistance
- Constant acceleration due to gravity (g)
- The projectile is a point object
- The slope is uniform and smooth throughout the motion
- These assumptions simplify calculations for board and competitive exams.
10. What are the real-life applications of projectile motion on an inclined plane?
Applications of projectile motion on an inclined plane include:
- Launching objects on hills or slopes in sports and engineering.
- Ballistics of military projectiles fired from elevated positions.
- Analysis in mining operations where debris lands on sloped surfaces.
- This topic links physics concepts to real-world scenarios found in exams and project work.
11. Derive the expression for the range of a projectile on an inclined plane.
The range (R) on an inclined plane is derived by resolving motion equations:
- Let u = initial velocity, θ = projection angle with the horizontal, α = slope angle, g = acceleration due to gravity.
- After resolving, R = (2u2 cosθ sin(θ – α)) / (g cos2α)
- This derivation is vital in CBSE board exams and competitive entrance tests.

































