




What Forces Keep Satellites in Orbit Around the Earth?
The motion of satellites of Earth refers to the movement of natural and artificial bodies in orbits due to the gravitational interaction between the satellite and the Earth. Understanding this motion involves concepts of circular motion, gravitation, and orbital mechanics, which are essential in JEE Physics.
Definition and Types of Satellites
A satellite is any object that revolves around a planet or star under the influence of gravity. Satellites are classified as natural, like the Moon, or artificial, which are man-made for communication, meteorology, and research purposes.
Nature of Satellite Motion
Satellites move in either circular or elliptical orbits around Earth, governed by the gravitational force between the Earth and the satellite. This force acts as the centripetal force required for orbital motion.
In circular motion, the velocity of the satellite is always tangent to its path, while the acceleration is directed towards the center of the orbit, that is, towards the center of the Earth.
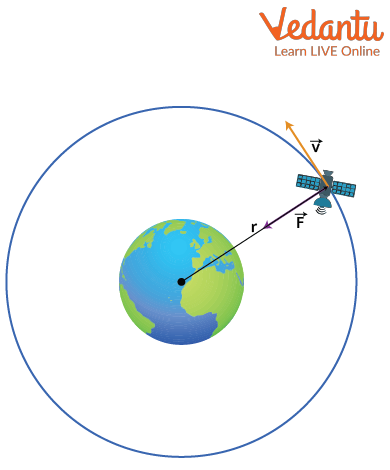
For elliptical orbits, the satellite's velocity is tangent to the ellipse at every point, while acceleration is directed towards the focus occupied by the Earth. The speed of the satellite varies at different points of its orbit in this case.
Forces Acting on a Satellite
The primary force responsible for keeping a satellite in orbit is gravity. The gravitational force acts as the centripetal force, ensuring that the satellite does not move in a straight line but follows a curved trajectory around the Earth.
The required centripetal force for a satellite of mass $m$ moving with orbital speed $v$ in a circular orbit of radius $r$ is given by $F_{\text{c}} = m\dfrac{v^2}{r}$. The gravitational pull of the Earth on the satellite is $F_{\text{g}} = G\dfrac{Mm}{r^2}$, where $M$ is the mass of the Earth and $G$ is the universal gravitational constant.
Equating centripetal and gravitational forces leads to the condition necessary for orbital motion:
$m\dfrac{v^2}{r} = G\dfrac{Mm}{r^2}$
This relationship determines the allowable orbital speed for stable satellite motion.
Orbital Velocity of Satellites
Orbital velocity refers to the minimum speed a satellite requires to maintain a stable orbit around Earth. This velocity ensures that the inertia of the satellite balances the gravitational pull without causing it to fall back or escape into space.
From the force balance, the orbital velocity $v_0$ for a satellite at a distance $r$ from the center of the Earth is:
$v_0 = \sqrt{\dfrac{GM}{r}}$
If a satellite orbits close to Earth's surface, $r$ is approximately the radius of the Earth ($R$), so $v_0 = \sqrt{gR}$, where $g$ is the acceleration due to gravity at Earth's surface. For higher altitudes, $r = R + h$, where $h$ is the altitude above the surface.
To study further details about satellite velocities and related derivations, refer to Orbital Velocity And Motion Of Satellites.
Escape Velocity and its Relation to Orbital Velocity
Escape velocity is the minimum velocity required for an object to escape Earth's gravitational field without further propulsion. It is related to the orbital velocity by $v_e = \sqrt{2}v_0$ for an object near Earth's surface.
| Quantity | Expression |
|---|---|
| Orbital Velocity $(v_0)$ | $\sqrt{\dfrac{GM}{r}}$ |
| Escape Velocity $(v_e)$ | $\sqrt{\dfrac{2GM}{r}}$ |
| Relation | $v_e = \sqrt{2} v_0$ |
Elliptical and Circular Orbits
In circular orbits, the speed of the satellite remains constant. In elliptical orbits, however, the speed varies; it is greatest at the perigee (nearest point to Earth) and least at the apogee (farthest point).
The Earth is always located at one focus of the elliptical path described by a satellite according to Kepler’s laws. The motion in these orbits follows the equations derived from Newton’s law of gravitation.
Applications and Examples of Satellites
Satellites serve purposes such as weather forecasting, communication, navigation, scientific research, and military surveillance. Artificial satellites are launched into specific orbits to fulfill these objectives.
- Weather satellites for meteorological observation
- Communication satellites for global transmission
- Navigation satellites for accurate location services
- Astronomical satellites for deep space study
Relevant Physical Concepts
The motion of satellites is fundamentally explained by Newton’s laws of motion and the law of universal gravitation. The interaction of centrifugal and centripetal forces and gravitational potential energy determine the dynamics of orbiting satellites.
Detailed understanding of these physical concepts is available at Newton's Laws Of Motion and Gravitation.
For the study of forces acting away from the center, the centrifugal force concept is discussed at Centrifugal Force.
Summary Table: Key Properties of Satellite Motion
| Parameter | Description |
|---|---|
| Mass of Satellite ($m$) | Negligible compared to Earth |
| Radius of Orbit ($r$) | $R + h$, where $R$ is Earth's radius |
| Orbital Period ($T$) | Time taken to complete one revolution |
| Orbital Velocity ($v_0$) | $\sqrt{\dfrac{GM}{r}}$ |
Important Concepts for JEE Preparation
Mastering satellite motion includes understanding gravitational potential energy, centripetal and centrifugal forces, and the derivations of orbital and escape velocities. These concepts frequently appear in JEE Physics questions.
Additional studies on gravitational potential energy relevant to satellite mechanics can be found at Gravitational Potential Energy.
FAQs on Understanding How Satellites Move Around Earth
1. What is the motion of satellites around the Earth?
The motion of satellites around the Earth is a type of uniform circular motion where satellites revolve in stable orbits due to the balance between gravitational force and their inertia.
Key points:
- Satellites follow a path called an orbit around the Earth.
- The centripetal force required for this motion is provided by the gravitational attraction of the Earth.
- Depending on their speed and altitude, satellites can be in geostationary or polar orbits.
- Examples include communication satellites and the International Space Station.
2. How does gravity affect the motion of a satellite?
Gravity is the force that keeps satellites in orbit around Earth by continually pulling them toward the planet.
Key details:
- Gravity acts as the centripetal force that bends the satellite’s straight motion into a curved path.
- Without gravity, the satellite would move in a straight line off into space.
- The balance between forward velocity and gravity allows satellites to circle the Earth continuously.
3. What is an artificial satellite?
An artificial satellite is a human-made object that is intentionally placed into orbit around Earth or another celestial body.
Common features include:
- Launched by rockets and used for communication, weather forecasting, navigation, and research.
- Examples: INSAT, GPS satellites, Hubble Space Telescope.
- Orbits can vary: geostationary, low Earth, or polar.
4. What is a geostationary satellite?
A geostationary satellite is a type of artificial satellite that orbits the Earth at the equator with an orbital period equal to the Earth's rotation period (24 hours).
Key facts:
- Remains fixed above one point over the equator.
- Altitude is approximately 36,000 km above Earth's surface.
- Used for communication and weather forecasting.
5. What factors determine the orbital speed of a satellite?
The orbital speed of a satellite depends on the gravitational force and the radius of its orbit.
Key determinants:
- Closer satellites must travel faster to counter stronger gravity.
- Speed is given by the formula v = √(GM/R), where G is the universal gravitational constant, M is Earth's mass, and R is the distance from the Earth's center.
- Higher altitude means lower speed needed for stable orbit.
6. What are the uses of artificial satellites?
Artificial satellites are used for numerous essential functions in modern society.
Main uses:
- Communication (TV, Internet, Phones)
- Weather Monitoring and forecasting
- Earth Observation and mapping
- Navigation Systems (GPS)
- Space research and scientific experiments
7. Why do satellites not fall back to Earth?
Satellites do not fall back to Earth because their forward speed creates enough inertia to balance Earth's gravity, resulting in a stable orbit.
Summary:
- They are in constant free-fall toward Earth but their sideways motion keeps missing the planet.
- Gravity pulls them toward Earth, while inertia keeps them moving forward.
- This combination creates a circular or elliptical orbit.
8. What is the difference between natural and artificial satellites?
Natural satellites are celestial bodies that orbit planets naturally, while artificial satellites are man-made and launched intentionally.
Comparison:
- Natural: Example – the Moon (Earth’s only natural satellite).
- Artificial: Created by humans; used for communication, research, etc.
- Both rely on gravity for their motion around planets.
9. How is the time period of a satellite in orbit calculated?
The time period of a satellite is the time it takes to complete one revolution in its orbit.
Formula and key facts:
- Given by T = 2π√(R3/GM)
- T: Time period, R: Orbital radius, G: Universal gravitational constant, M: Mass of Earth
- Higher orbit = Longer period
10. What is the escape velocity of Earth and why is it important for satellite launch?
The escape velocity of Earth is the minimum speed an object must reach to break free from Earth's gravitational pull without further propulsion.
Key details:
- For Earth, escape velocity is about 11.2 km/s.
- Essential for launching satellites, as it ensures they can enter into orbit or leave Earth's atmosphere.
- Satellites are launched with speeds approaching escape velocity for intended orbits.
























