



What is an Electric Field?
The field of electrostatics had the main purpose of explaining the field created by a charged particle known as an electric field. When a charge is sitting in a space, field lines emanate from it which is collectively given the name of an electric field capable of influencing other charges nearby.
Depending on the nature of the charge, i.e., positive or negative, the field line directions are also different. In positive charge, the field lines go out while in negative charge the field lines are directed inwards as shown in the figure below. The electric field can exert electrostatic force on other static or moving charges in the vicinity of the test charge. This force can be either repulsive or attractive depending on the nature of the charges.
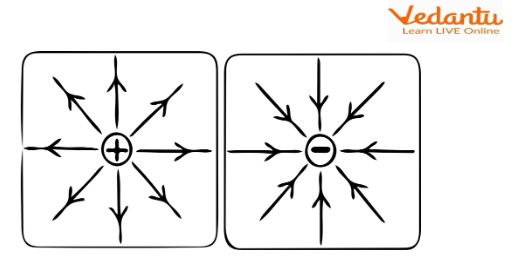
Field Lines of a Positive and Negative Charge
Derivation of the Electric Field of a Charged Particle (Point Charge)
Let us derive the electric field due to a point charge from the expression of electrostatic force.
Consider a source charge of magnitude ${{q}_{0}}$. Now, let a test charge of magnitude $q$ is placed in the vicinity of the test charge, as a result of which both will experience a force either repulsive or attractive depending on the sign of the charges. In electrostatics, this force follows inverse square law, i.e., the force magnitude drops according to the squared increase in the distance r between the charges. Also, this force is directly proportional to the product of the charges.
So, the expression is
$F\propto {{q}_{0}}q$ and $F\propto \dfrac{1}{{{r}^{2}}}$
$\left| F \right|=k\dfrac{{{q}_{0}}q\ }{{{r}^{2}}}$
Here, k is the constant of proportionality and has the value of
$k=\dfrac{1}{4\pi {{\varepsilon }_{0}}} $
$=9\times {{10}^{9}}\ \text{N}{{\text{m}}^{\text{2}}}{{\text{C}}^{\text{-1}}} $
The space around the source charge ${{q}_{0}}$ in which the test charge experiences the force is the electric field due to the source charge ${{q}_{0}}$.
Now, the strength of the electric field at a particular point is the electric field intensity and can be defined as the force experienced by a charge at that particular point. The expression is
$\vec{E}\left( r \right)=\dfrac{\vec{F}\left( r \right)}{q}$
The electric field is a vector quantity and is directed along the line of force experienced by the test charge, i.e., the direction along which the test charge tends to move.
Motion of Charged Particle in an Electric Field
Any motion is best defined by the equation of the particle’s trajectory. Let us find the displacement equation of the motion of a point charge in an electric field. Force experienced by a point electric charge either in rest or in motion due to an electric field is
$\vec{F}=q\vec{E}$
When q is positive, the force experienced is parallel to $\vec{E}$. When q is negative, the force experienced is opposite to $\vec{E}$ as shown in the figure below.
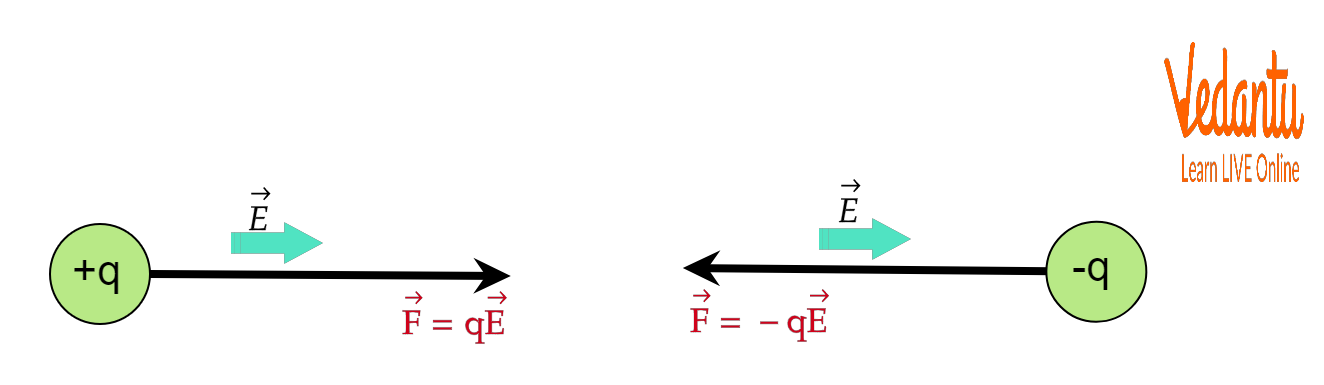
Force Experienced by Charged Particle in Electric Field
Now, we know from Newton’s Law of motion,
$\vec{F}=m\vec{a}$
Here,
$m$ is the mass of the charged particle and $\vec{a}$ is the acceleration.
So,
$ \vec{a}=\dfrac{{\vec{F}}}{m} $
$ =\dfrac{q\vec{E}}{m} $
$ =\text{constant} $
Here, the electric field is uniform and other quantities for a charged particle are constant. Also, this has been derived by neglecting the force of gravity (assumed to be balanced by some other external force).
Now, from the equations of motion of a particle, the velocity and displacement relations are
$ v=u+at $
$ s=ut+\dfrac{1}{2}a{{t}^{2}} $
If initially the particle is at rest, then $u=0$. Then the equations become
$ v=at=\dfrac{qE}{m}t $
$ s=\dfrac{1}{2}\left( \dfrac{qE}{m} \right){{t}^{2}} $
When the particle projection is perpendicular to the direction of the electric field, then motion is in the upward direction (along the y-axis). So,
$y=\dfrac{1}{2}\left( \dfrac{qE}{m} \right){{t}^{2}}$
Now, $t=\dfrac{x}{v}$, where x is the distance travelled by the particle under the influence of electric field and v is the drift velocity attained. Eliminating the time t in the above equation, we get,
$y=\dfrac{1}{2}\left( \dfrac{qE}{m} \right){{\left( \dfrac{x}{v} \right)}^{2}}$
So, we see that the y-x relation is actually a parabola. Therefore, the particle follows a parabolic trajectory.
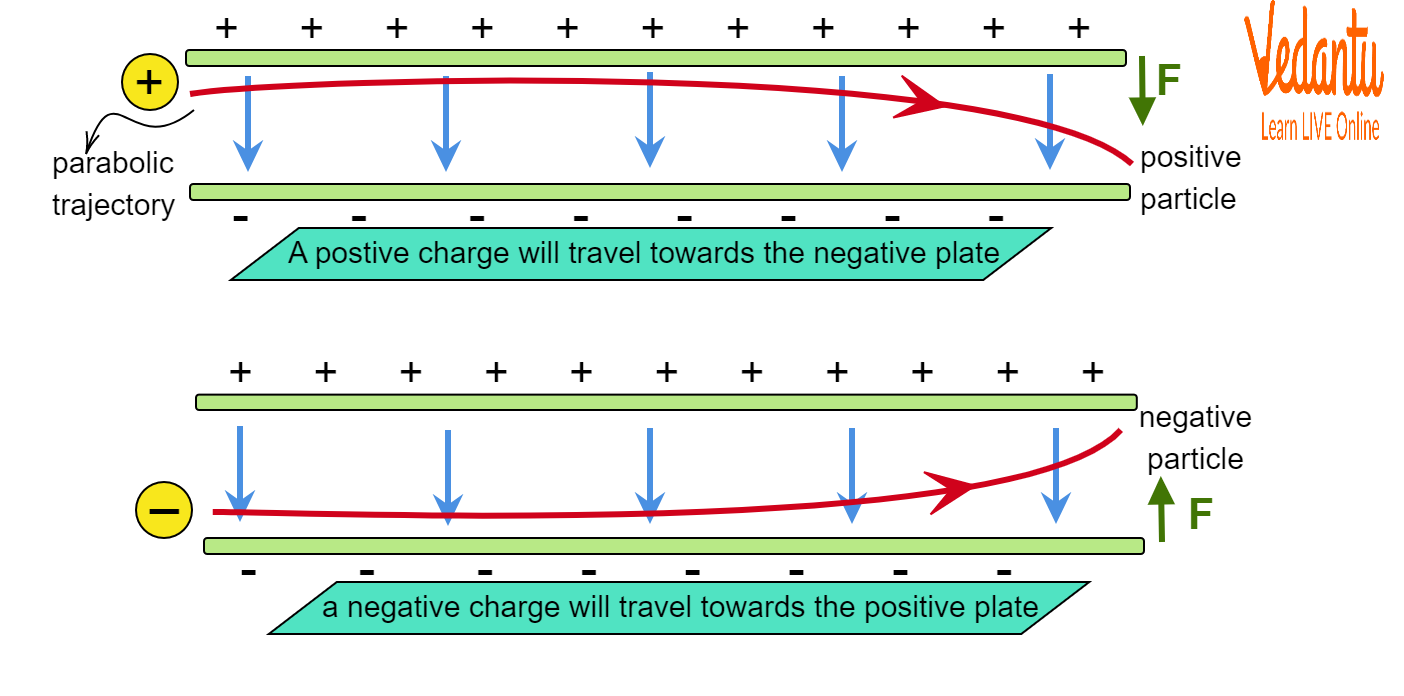
Trajectory of Charged Particles in Electric Field
Summary
The following points can be concluded for the topic:
The density of electric field lines tells us about the electric field intensity at that point.
The motion of a charged particle in an electric field depends on the direction of the electric field.
The electric field is the space where charged particles experience a force of attraction or repulsion due to a source charge.
The motion of a charged particle in an electric field is parabolic in nature.












FAQs on Charged Particle Motion in an Electric Field for JEE
1. What is the direction of a charged particle in an electric field?
If the charge is positive, it will move in the direction of the electric field. If the charge is negative, the motion will be opposite to the electric field. So when the charge is positive, then it moves following a parabolic path toward the negative plate and when the charge is negative, the motion is parabolic towards the positive plate.
2. Why does the trajectory of particles in an electrical field bend?
The electric field produced in between two plates, one positive and one negative, causes the particle to move in a parabolic path. The positive plate will attract the charged particle if it is negatively charged while the negative plate will repel it. So, the balanced force of the two plates will cause the trajectory to have a bent appearance.
3. What happens to the motion of a charged particle when a magnetic field is also applied along with an electric field?
The charged particle experiences a Lorentz Force which is expressed as
$\vec{F}=q\left( \vec{E}+\ \left( \vec{v}\times \vec{B} \right) \right)$
The particle trajectory is dependent on how the particle is entering the fields, i.e., the angle it makes with the direction of the magnetic and electric fields. If the particle is making an angle of ninety degrees with the direction of the magnetic field and the particle bends into a circular track. Now the electric field will produce a translation to the charge in its direction. So, the end trajectory is a helix. As the directions in the question and the angle between the charge motion are not mentioned, the trajectory cannot be determined accurately. In order to have a definite trajectory, we need to know these factors.




