




Key Principles and Formulas for Motion in Two Dimensions
Motion in two dimensions, also called 2D motion, describes the movement of objects restricted to a plane with both horizontal and vertical components. It is an essential concept in physics and is fundamental for solving problems involving projectiles, uniform circular motion, and other planar trajectories.
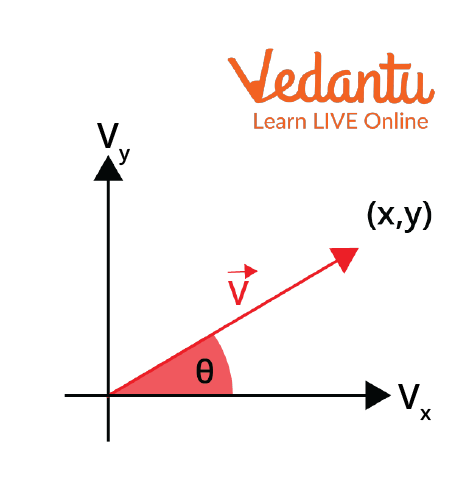
Definition of Motion in Two Dimensions
Two-dimensional motion occurs when an object's position changes simultaneously along two mutually perpendicular axes, conventionally denoted as x and y. Both displacement and velocity have components along each axis, which must be analyzed using vectors and resolved for accurate assessment.
Comparison: 1D, 2D, and 3D Motion
Physical motion may occur along one, two, or three spatial dimensions. The method of analysis and the equations used differ depending on the number of axes involved in the motion.
| Type of Motion | Description |
|---|---|
| 1D Motion | Change along a single axis (x or y) |
| 2D Motion | Simultaneous change along x and y axes |
| 3D Motion | Change along x, y, and z axes |
Simple examples of 2D motion include a ball projected at an angle (projectile motion), circular motion in a plane, or a car taking a curved turn on a flat road. Each case requires vector decomposition and analysis of components.
Kinematic Equations for Motion in 2D Dimensions
In two-dimensional kinematics, the motion is analyzed by splitting it into independent x and y directions. Standard equations for constant acceleration apply to each axis separately, facilitating calculations related to displacement, velocity, and acceleration.
| Quantity | Equation |
|---|---|
| Displacement in x | $s_x = u_x t + \dfrac{1}{2} a_x t^2$ |
| Displacement in y | $s_y = u_y t + \dfrac{1}{2} a_y t^2$ |
| Velocity in x | $v_x = u_x + a_x t$ |
| Velocity in y | $v_y = u_y + a_y t$ |
| Resultant velocity | $v = \sqrt{v_x^2 + v_y^2}$ |
For resultant displacement or velocity, both components are combined using the Pythagorean theorem, ensuring vector nature is considered accurately. Axes must be chosen carefully and initial velocity components resolved appropriately.
Projectile Motion: The Classic 2D Case
Projectile motion exemplifies two-dimensional motion with a constant acceleration along the vertical axis and zero or constant acceleration along the horizontal axis. The equations below are widely used in entrance examinations and are based on neglecting air resistance.
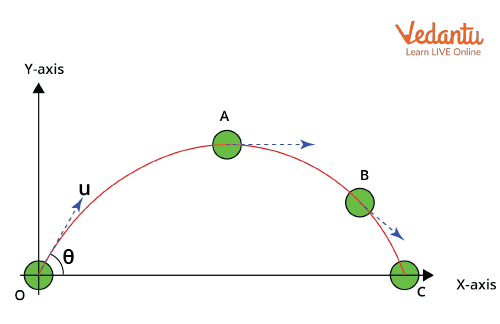
For an initial velocity $u$ at an angle $\theta$ to the horizontal: $u_x = u \cos\theta$, $u_y = u \sin\theta$. The horizontal and vertical positions at time $t$ are:
$s_x = (u \cos\theta) t$
$s_y = (u \sin\theta) t - \dfrac{1}{2} g t^2$
Maximum height ($H$): $H = \dfrac{u^2 \sin^2\theta}{2g}$
Time of flight ($T$): $T = \dfrac{2u \sin\theta}{g}$
Horizontal range ($R$): $R = \dfrac{u^2 \sin2\theta}{g}$
Projectile motion always follows a parabolic trajectory, and each axis is treated independently for calculations. Concepts from the Motion of Charge Particle in Electric Field can further reinforce understanding of planar motion under constant forces.
Solved Example: Motion in 2D Dimensions
A stone is projected with $u = 20\,\mathrm{m/s}$ at an angle $\theta = 30^\circ$. Calculate the horizontal range and maximum height. Use $g = 9.8\,\mathrm{m/s^2}$.
Resolved components: $u_x = 20 \times \cos30^\circ = 17.32\,\mathrm{m/s}$, $u_y = 20 \times \sin30^\circ = 10\,\mathrm{m/s}$.
Horizontal range: $R = \dfrac{u^2\sin2\theta}{g} = \dfrac{400 \times 0.5}{9.8} \approx 20.4\,\mathrm{m}$
Maximum height: $H = \dfrac{u^2\sin^2\theta}{2g} = \dfrac{400 \times 0.25}{19.6} \approx 5.1\,\mathrm{m}$
Time to reach maximum height: $t = \dfrac{u_y}{g} = \dfrac{10}{9.8} \approx 1.02\,\mathrm{s}$
Common Mistakes in Solving 2D Motion Problems
Careless use of kinematic equations or improper vector analysis often results in errors. It is recommended to always resolve vectors, pay attention to units, and confirm the direction of each component before computation.
- Neglecting to resolve vectors into x and y parts
- Combining vector quantities directly without vector addition
- Assuming acceleration acts in all directions
- Ignoring negative or positive signs
- Not using diagrams to visualize components
Carefully check which direction has acceleration and which direction remains uniform, especially in projectile and circular motion. For more targeted practice on these topics, the Kinematics Mock Test 1 provides a focused question set for JEE preparation.
Circular Motion as a Two-Dimensional Example
Uniform circular motion is also classified as motion in two dimensions. The object moves at constant speed along a circular path in a plane, and the velocity's direction changes continuously even though its magnitude remains the same.
- Speed is constant; direction changes
- Acceleration (centripetal) always points to center of circle
- Motion is confined to a plane (x and y axes)
For formula derivations and further problems on plane motion, refer to the Kinematics Mock Test 2 and Kinematics Mock Test 3.
Detailed Analysis and Calculation Approach
Every two-dimensional motion problem should start with drawing a diagram and resolving the initial velocity into its perpendicular components. Each axis is treated separately for computation using standard kinematic equations.
The resultant speed or displacement at any instant is found by vector addition: $v = \sqrt{v_x^2 + v_y^2}$, $s = \sqrt{s_x^2 + s_y^2}$. The direction is calculated using $\tan \alpha = \dfrac{v_y}{v_x}$ or similar trigonometric analysis.
Units and sign conventions must be carefully maintained. All accelerations must be checked for constancy before directly applying the equations provided above. The Kinetic Theory of Gases also explores the motion of particles in multiple dimensions.
Key Concepts and Fast Revision points
- Always resolve velocities and accelerations into x and y
- Check which axes experience constant acceleration
- Use vector addition for total velocity and displacement
- Draw diagrams to visualize motion and components
- Apply trigonometric formulae correctly
- Label axes and maintain consistent units throughout calculations
Consistent revision and practice of 2D dynamics, including the Dimensions of Speed, ensures conceptual clarity and helps avoid standard student mistakes in examinations.
FAQs on Understanding Motion in 2D Dimensions for Students
1. What is motion in two dimensions?
Motion in two dimensions refers to the movement of an object in a plane, involving both the x- and y-axes. Key features include:
- Object changes position along two coordinate axes (x and y).
- Example cases include projectile motion, circular motion, and motion in fields.
- Requires vector analysis to describe displacement, velocity, and acceleration.
2. What is projectile motion?
Projectile motion is a type of two-dimensional motion where an object moves simultaneously in the horizontal and vertical directions under the influence of gravity.
- The path followed is typically a parabola.
- Both horizontal velocity and vertical acceleration due to gravity act on the object.
- Key examples: a thrown ball, a bullet, or a stone thrown from a mountain.
3. What are the kinematic equations for motion in two dimensions?
The kinematic equations for two-dimensional motion describe how position, velocity, and acceleration change with time:
- Horizontal: x = u_x t + (1/2) a_x t^2
- Vertical: y = u_y t + (1/2) a_y t^2
- Velocity: v_x = u_x + a_x t; v_y = u_y + a_y t
4. What is relative velocity in two dimensions?
Relative velocity in two dimensions is the velocity of one object as observed from another moving object.
- It is a vector sum/difference: VAB = V_A - V_B
- Used in problems like boats in rivers and airplanes in wind.
- Requires resolving velocities into x and y components.
5. How do you calculate the time of flight, range, and maximum height in projectile motion?
Time of flight, range, and maximum height are key parameters in projectile motion:
- Time of Flight (T): T = (2u sinθ)/g
- Range (R): R = (u^2 sin2θ)/g
- Maximum Height (H): H = (u^2 sin^2θ)/(2g)
6. What are the main differences between one-dimensional and two-dimensional motion?
One-dimensional motion occurs along a straight line, while two-dimensional motion occurs in a plane. Key differences:
- 1D: Only one coordinate changes (x or y).
- 2D: Both coordinates change simultaneously.
- 2D motion requires vector analysis (adding components).
- Examples: 1D – car on a straight road; 2D – football kicked in air.
7. What are some real-life examples of motion in two dimensions?
Common examples of two-dimensional motion include:
- Projectile motion of a cricket ball or basketball.
- Satellite orbiting Earth (in a plane).
- Car taking a turn on a curved road.
- Riverboat crossing a flowing river.
8. What is the significance of vectors in studying two-dimensional motion?
In two-dimensional motion, vectors are essential to describe displacement, velocity, and acceleration.
- Allows analysis of each component (x/y axis) separately.
- Enables correct computation of resultant quantities.
- Makes solving problems with direction and magnitude easier.
9. How do you resolve a vector into its components in two dimensions?
Resolving a vector means breaking it into horizontal (x-axis) and vertical (y-axis) components.
- If magnitude is V at angle θ with horizontal:
- Horizontal Component: Vx = V cosθ
- Vertical Component: Vy = V sinθ
- Components allow for easier addition and subtraction of vectors.
10. Can you explain uniform circular motion as a special case of motion in two dimensions?
Yes, uniform circular motion is a type of two-dimensional motion where an object moves in a circle at constant speed.
- The direction of velocity changes continuously, though speed remains constant.
- Acceleration is always directed towards the center (centripetal).
- Used in cases like a stone tied with string and rotated or movement of planets.
























