Half Life of Zero Order Reaction for JEE

The order of a reaction is an experimentally determined quantity and not a theoretical one. It can be zero, positive, negative, or fractional with respect to a reactant. While knowing about the half-life of a zero order reaction, it is necessary to know what a zero order reaction means. The key concept of zero order reaction is that, in a zero order reaction, the rate of the reaction will never depend on the concentration of the reacting species.

Half-life is the concept of time, so the word is sometimes used as the half time of zero order reaction. But note that the correct usage is half-life period, not half time. 

Half Life Equation for Zero Order reaction 

Half-life is the time required to consume half of the initial concentration of a reacting species (represented as $t_{{\displaystyle \frac{1}{2}}}$). Thus the half-life of a zero order reaction can be determined by taking the final concentration of the reacting species as half of its initial concentration and applying this relation in the rate equation for zero order reaction. 

For a zero order reaction, the rate will be proportional to the zeroth power of concentration of reactants. If we consider a reaction 

$A\to \text{ products }$

The rate of the reaction, if it is zero order, will be

$\begin{array}{rl}\text{ rate }& =-{\displaystyle \frac{d[A]}{dt}}\\ & =k[A{]}^0\\ & =k\end{array}$

dA is the difference between initial and final concentration at a given time interval of dt (tfinal – tinitial).

So the above equation becomes

$-{\displaystyle \frac{[A{]}_{\text{final }}-[A{]}_{\text{initial }}}{t_{\text{final }}-t_{\text{initial }}}}=k$

Or 

${\displaystyle \frac{[A{]}_{\text{final }}-[A{]}_{\text{ initial }}}{t_{\text{final }}-t_{\text{initial }}}}=-k$

In the half-life period, if the initial concentration of A is taken as [A]0, then at $t_{{\displaystyle \frac{1}{2}}}$ the concentration becomes its half , that is ${\displaystyle \frac{[A{]}_0}{2}}$. Substitute this in the above equation.

$\begin{array}{rl}& {\displaystyle \frac{{\displaystyle \frac{[A{]}_0}{2}}-[A{]}_0}{t_{{\displaystyle \frac{1}{2}}}-0}}=-k\\ & {\displaystyle \frac{[A{]}_0}{2}}-[A{]}_0=-k\times t_{{\displaystyle \frac{1}{2}}}\\ & {\displaystyle \frac{-[A{]}_0}{2}}=-k\times t_{{\displaystyle \frac{1}{2}}}\\ & t_{{\displaystyle \frac{1}{2}}}={\displaystyle \frac{[A{]}_0}{2k}}\end{array}$

Thus the half-life period of zero order reaction is equal to ${\displaystyle \frac{[A{]}_0}{(2k)}}$ and so will be directly proportional to the concentration of the reactant and it is inversely proportional to the rate constant of the reaction.

Integrated Rate Law of Zero Order Reaction 

We have already seen that the rate of zero order reaction can be written as 

$\begin{array}{r}-{\displaystyle \frac{d[A]}{dt}}=k[A{]}^0\\ d[A]=-kdt\end{array}$

Integrate the above equation so that we get

$\begin{array}{rl}& {\int }_{[A{]}_0}^{[A{]}_t}d[A]=-k{\int }_0^{t}dt\\ & [A{]}_t-[A{]}_0=-k[t-0]\\ & [A{]}_t-[A{]}_0=-kt\end{array}$

Rearranging we get,

$[A{]}_0-[A{]}_t=kt$

Where $[A{]}_0$ is the initial concentration and $[A{]}_t$ is the concentration at time t.

The equation $[A{]}_0–[A{]}_t=kt$ is called the integrated rate law of zero order reaction.

Different Types of Graph for a Zero Order Reaction

Concentration versus Time Graph

The integrated rate law $[A{]}_0–[A{]}_t=kt$ can also be written as

$[A{]}_t=-kt+[A{]}_0$

This equation exactly looks like the equation of a straight line (y= mx+c) where m is the slope and c is the intercept. If we compare this with the above equation, we will get the slope as –k and intercept as $[A{]}_0$ for a graph of $[A{]}_t$ in y axis and time t in x axis. 

Always keep in mind that while rearranging the equation $[A{]}_t$ should be on the left side. Since $[A{]}_0$ is the initial concentration, what is varying is the concentration with time t, so, $[A{]}_t$ should be taken in y axis.

Therefore, the graph of concentration Vs time of zero order reaction will look like a straight line with negative slope.

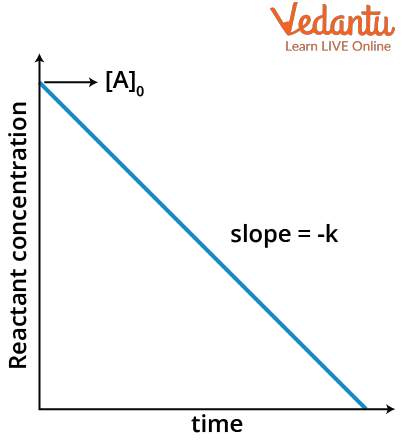
Concentration versus Time graph for zero order reaction

Note that this graph is valid only up to a certain limit of time. The graph will not be valid after the time reaches a value where the concentration becomes zero because if the graph is valid throughout, the extension of the graph (red line) will give a negative concentration which is not possible. 

Reactant Rate versus Concentration Graph

Rate of zero order reaction is;

$\text{ Rate }=\mathrm{k}[\mathrm{A}{]}_0=\mathrm{k}$

That rate is independent of the concentration of reactant and thus will be a straight line with slope zero.

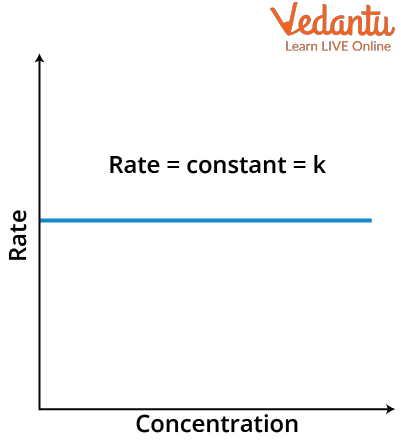
Rate versus Concentration graph of zero order reaction

Half-Life versus Initial Concentration Graph

We know that the  half-life of a zero order reaction is given by

$t_{{\displaystyle \frac{1}{2}}}={\displaystyle \frac{[A{]}_0}{2k}}$

which is again in the form of y= mx+c where y here will be equal to $t_{{\displaystyle \frac{1}{2}}}$ and x will be equal to $[A{]}_0$  with m as ${\displaystyle \frac{1}{2k}}$ and intercept will be zero. Thus the graph will look like as follows

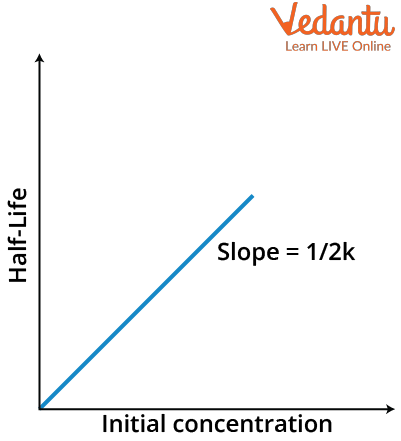
Half-Life versus Initial Concentration graph of zero order reaction

Examples of Zero Order Reaction

• Photochemical reaction of hydrogen and chlorine

• N2O decomposition of hot platinum surface

• Decomposition of NH3 in presence of molybdenum or tungsten

• Decomposition of HI on gold surface

• Reaction of Iodine with acetone in presence of H+ ion

Conclusion

In a half-life, 50 % of the reactant will get consumed. Calculating half-life is very useful in many reactions especially in pharmaceutical fields. For example, half-life can be used to determine the dose of medicine to be taken by a patient. 

A reaction with a long half-life period will take much time for the completion of the reaction, and thus it will take a long time to give the complete effect of the reaction (for example, the effect of medicine on a patient).