




How Does Rotation Work in Complex Numbers?
The concept of rotation in complex numbers is essential for JEE Main as it establishes a direct correspondence between algebraic operations and geometric transformations in the Argand plane. This article rigorously explores the rotation concepts, foundational theorems, derivations, and key examples required for a comprehensive understanding at the JEE level.
Complex Numbers in the Argand Plane
A complex number $z = x + iy$ is represented as a point $(x, y)$ in the Argand (complex) plane, where $x$ is the real part and $y$ is the imaginary part. The modulus $|z|$ gives the distance from the origin, and the argument $\arg(z)$ specifies its angle from the positive real axis.
The geometric interpretation supports algebraic operations: addition corresponds to vector addition, and multiplication encodes stretching and rotation. This duality is central to many higher-level results in [Understanding Complex Numbers](https://www.vedantu.com/jee-main/maths-complex-numbers).
Defining Rotation of a Complex Number
The rotation of a complex number involves turning its geometric representation by a certain angle about the origin. Algebraically, this is achieved by multiplying the number by a complex number of unit modulus (unimodular), commonly written as $e^{i\theta}$, which corresponds to a rotation by angle $\theta$ radians.
If $z$ is a complex number and $\alpha$ a real number, then the complex number $z' = z \cdot e^{i\alpha}$ represents the image of $z$ obtained by rotating it anti-clockwise by angle $\alpha$ about the origin. For clock-wise rotation, one uses $e^{-i\alpha}$ as the multiplier.
Algebraic Structure of Complex Rotation
Express $z$ in polar form as $z = r e^{i\theta}$, where $r = |z|$ and $\theta = \arg(z)$. Then, the rotated number is:
$$z' = z \cdot e^{i\alpha} = r e^{i(\theta + \alpha)}$$
Thus, multiplying a complex number by $e^{i\alpha}$ increases its argument by $\alpha$ but keeps its modulus unchanged.
Geometric Meaning and Properties
The transformation $z \mapsto z e^{i\alpha}$ rotates every point in the Argand plane by $\alpha$ radians about the origin. The modulus remains the same, confirming that pure rotation does not affect distance from the origin.
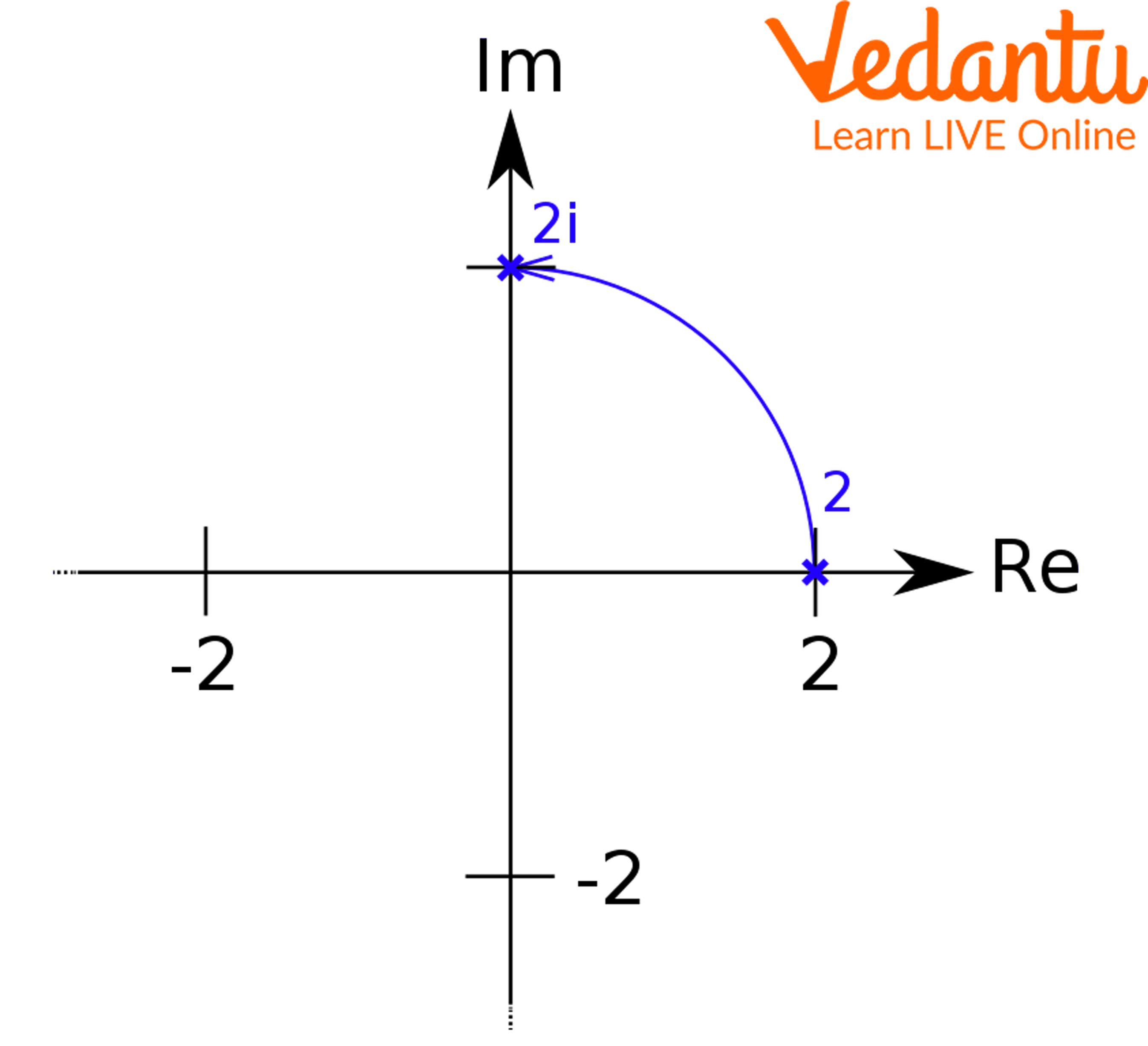
Multiplication by $i = e^{i\frac{\pi}{2}}$ rotates any complex number by $\dfrac{\pi}{2}$ radians (90 degrees) anti-clockwise. More generally, multiplication by $e^{in\pi/2}$ gives rotations by integral multiples of right angles.
Rotation Between Two Points: Ratio of Complex Numbers
Let $z_1 = r_1 e^{i\theta_1}$ and $z_2 = r_2 e^{i\theta_2}$ be two non-zero complex numbers (not collinear with the origin). The quotient $\dfrac{z_1}{z_2}$ is given by:
$$\dfrac{z_1}{z_2} = \dfrac{r_1}{r_2} e^{i(\theta_1 - \theta_2)}$$
Here, $|\dfrac{z_1}{z_2}| = \dfrac{r_1}{r_2}$ gives the ratio of distances from the origin, and $\arg(\dfrac{z_1}{z_2}) = \theta_1 - \theta_2$ is the angle by which the vector $oz_2$ must be rotated to coincide with $oz_1$.
Rotation Theorem for Directed Segments
Given points $A(z_1)$ and $B(z_2)$, the directed segment $\overrightarrow{AB}$ is represented by $z_2 - z_1$. Let $C(z_3)$ and $D(z_4)$ define another segment $\overrightarrow{CD} = z_4 - z_3$. Then, the ratio:
$$\dfrac{z_4 - z_3}{z_2 - z_1} = \left|\dfrac{z_4 - z_3}{z_2 - z_1}\right| e^{i\theta}$$
Here, $|\cdots|$ gives the ratio of lengths, and $\theta = \arg\left(\dfrac{z_4-z_3}{z_2-z_1}\right)$ is the angle by which $\overrightarrow{AB}$ must be rotated and stretched to align with $\overrightarrow{CD}$. When only pure rotation is desired (no stretching), the modulus must be $1$.
Special Cases of Rotation
Multiplying any $z$ by a unimodular complex number ($|w|=1$) effects a pure rotation. For instance, multiplication by $i$ ($e^{i\pi/2}$) rotates by $90^\circ$ anti-clockwise. Multiplication by $-1$ ($e^{i\pi}$) rotates by $180^\circ$, and so forth.

When two complex numbers have the same modulus and their quotient is unimodular, they lie on a circle of radius $|z|$ centered at the origin, differing only by a rotation.
Stepwise Derivation: General Rotation Formula
Let $z$ be represented as $z = r e^{i\theta}$ and suppose we wish to rotate $z$ by an angle $\alpha$ about the origin. The rotated number is $z' = r e^{i(\theta + \alpha)}$.
This can also be written as $z' = z \cdot e^{i\alpha}$, reflecting the additive property of arguments in exponentials.
Alternatively, in rectangular form:
$$z' = (x + i y)(\cos\alpha + i \sin\alpha)$$
Expanding yields:
$$z' = (x\cos\alpha - y\sin\alpha) + i(x\sin\alpha + y\cos\alpha)$$
The real and imaginary parts transform as a standard planar rotation, confirming geometric intuition.
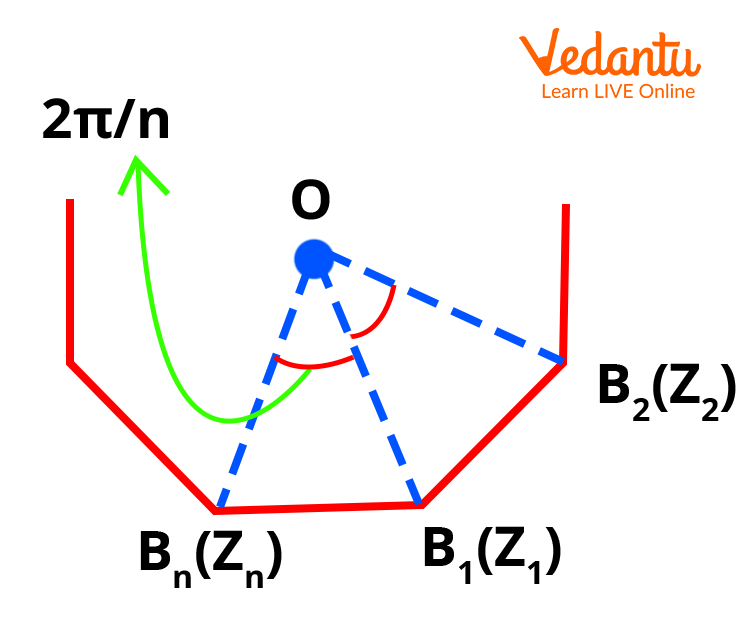
Rotation and Regular Polygons
For a regular $n$-gon centered at the origin, vertices are separated by equal angles $2\pi/n$. If $z_1$ represents one vertex, then after rotation by $2\pi/n$, the adjacent vertex is $z_2 = z_1 e^{i(2\pi/n)}$, the subsequent vertex by $z_k = z_1 e^{i 2\pi (k-1)/n}$.
This formulation is foundational for [Geometry of Complex Numbers](https://www.vedantu.com/jee-main/maths-geometry-of-complex-numbers) problems involving symmetries and rotational invariance.
Illustrative Examples
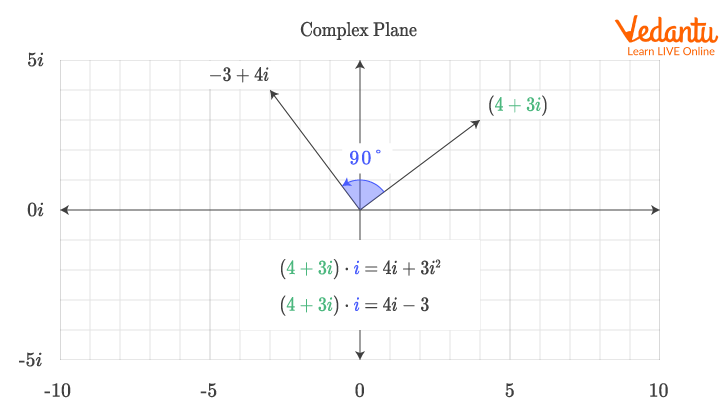
Example 1: Rotate the complex number $z = 5 + 6i$ by $90^\circ$ anti-clockwise about the origin.
To rotate by $90^\circ$, multiply by $i$:
$$(5 + 6i) \cdot i = 5i + 6i^2 = 5i + 6(-1) = -6 + 5i$$
Thus, the rotated complex number is $-6 + 5i$.
Example 2: Given vertices $z_1$, $z_2$, and $z_3$ of an isosceles right triangle with right angle at $z_3$ (i.e., at $R$), show that $(z_1 - z_2)^2 = 2(z_1 - z_3)(z_3 - z_2)$.
Since $PQ = QR$ and the angle at $R$ is $90^\circ$, the segment $z_2 - z_3$ must be a $90^\circ$ rotation of $z_1 - z_3$. Thus:
$$z_2 - z_3 = i(z_1 - z_3)$$
Squaring both sides:
$$(z_2 - z_3)^2 = i^2 (z_1 - z_3)^2 = - (z_1 - z_3)^2$$
Expanding $(z_1 - z_2)^2$ and substituting gives $(z_1 - z_2)^2 = 2(z_1 - z_3)(z_3 - z_2)$, as required.
Applications and Extended Observations
Rotation of complex numbers provides powerful tools for analyzing symmetries, geometric loci, and transformations within the complex plane. It is foundational for advanced results in [Complex Numbers and Quadratic Equations](https://www.vedantu.com/jee-main/maths-complex-numbers-and-quadratic-equations) and mathematical problem-solving strategies in coordinate geometry and trigonometric contexts.
Furthermore, the concept is central to the manipulation of complex loci, proof of results in cyclic quadrilaterals, and the geometric interpretation of complex inequalities.
Rotation and Unimodular Numbers
A unimodular complex number satisfies $|w| = 1$. Any multiplication by such a number results in pure rotation without change in magnitude. These numbers lie on the unit circle in the Argand plane and are of the form $e^{i\theta}$ for real $\theta$.
If $z_1$ and $z_2$ are complex numbers such that $|\dfrac{z_1}{z_2}|=1$, their arguments differ by a definite angle, and their magnitudes are equal.
Key Formulas and Summary Table
| Concept | Formula/Explanation |
|---|---|
| General Rotation | $z' = z \cdot e^{i\alpha}$ |
| Polar Form | $z = r e^{i\theta}$ |
| Argument Change | $\arg(z') = \arg(z) + \alpha$ |
| Quotient Rotation | $\dfrac{z_1}{z_2} = \dfrac{r_1}{r_2} e^{i(\theta_1-\theta_2)}$ |
| Multiplication by $i$ | $+90^\circ$ Rotation |
| Unit Modulus | $|e^{i\theta}| = 1$ |
Conclusion: The Significance of Complex Number Rotation
The concept of rotation within the framework of complex numbers tightly couples algebraic operations with geometric intuition. Mastery of this correspondence is indispensable for mathematical reasoning in competitive exams and advanced geometry topics.
Further study on [Polar Form of Complex Numbers](https://www.vedantu.com/jee-main/maths-polar-and-eular-form-of-a-complex-number) and [Modulus of Complex Numbers](https://www.vedantu.com/jee-main/maths-complex-numbers-detailed-discussion-on-modulus) will strengthen foundational understanding and enable application of rotation methods to a wide class of problems.
Practice with [Practice Paper on Complex Numbers](https://www.vedantu.com/jee-main/maths-complex-numbers-and-quadratic-equations-practice-paper) to consolidate these principles through typical examination problems and deepen conceptual integration.
FAQs on Understanding Rotation in Complex Numbers
1. What is the concept of rotation in complex numbers?
The concept of rotation in complex numbers refers to rotating a point in the complex plane about the origin using multiplication by a unit complex number. When a complex number z is multiplied by eiθ (where θ is the angle of rotation), the result is:
- Argand plane–the point rotates by θ radians about the origin.
- Multiplication by cis θ or eiθ rotates z by θ.
2. How does multiplying a complex number by 'i' affect its position in the Argand plane?
Multiplying a complex number by 'i' rotates it 90 degrees counterclockwise in the Argand plane. The steps are:
- If z = x + iy, then i·z = -y + ix
- This rotation does not change the modulus, only the argument
- Used for converting between perpendicular directions in questions on loci and geometry
3. How can you represent rotation of a complex number by an angle θ?
Rotation of a complex number by θ can be written as z' = z·eiθ or z' = z·(cos θ + i sin θ). To summarise:
- z' = z rotated by θ about the origin
- eiθ is Euler's formula, linking trigonometry and complex numbers
- This formula is used in geometry, vectors and CIRCLE/LOCUS based problems
4. What is the geometric interpretation of multiplying two complex numbers?
Multiplying two complex numbers results in:
- Their moduli multiply
- Their arguments (angles) add up
5. What is the significance of rotation in complex numbers for competitive exams?
Rotation using complex numbers simplifies geometry transformations, vector problems and locus. Its importance lies in:
- Simplifying calculation of new positions after rotation
- Helping draw loci and solve transformation questions
- Supporting angle-based proofs using Euler's Formula
- Frequent use in questions involving triangles, circles, and polygons
6. What is the formula for rotating a point (x, y) by an angle θ using complex numbers?
To rotate a point (x, y) by an angle θ about the origin, represent it as z = x + iy and use:
- z' = z · eiθ or z' = (x + iy)(cos θ + i sin θ)
- The new point's coordinates are (x' = x cos θ - y sin θ, y' = x sin θ + y cos θ)
7. Explain the use of Euler's formula in the rotation of complex numbers.
Euler's formula states that eiθ = cos θ + i sin θ.
- It is used to express rotation as multiplication by eiθ
- This connects trigonometry and complex numbers
- Important for solving many standard CBSE and entrance exam problems involving rotation and symmetry
8. How do you rotate a complex number about a point other than the origin?
To rotate a complex number z about a point a (not the origin) by angle θ:
- Translate so that a becomes the origin: z - a
- Rotate: (z - a)·eiθ
- Translate back: z' = a + (z - a)·eiθ
9. What are some real-world applications of complex number rotations?
Complex number rotations are applied in:
- Electrical engineering – analysing AC circuits and phasors
- Computer graphics – rotating objects in 2D space
- Robotics – describing rotational movement
- Physics simulations and signal processing
10. What is the locus of points generated by rotating a complex number z₀ by all angles between 0 and 2π?
The locus of the point z₀·eiθ as θ varies from 0 to 2π is a circle of radius |z₀| centred at the origin in the Argand plane. Key points:
- This illustrates how complex multiplication by eiθ generates a circle
- Frequently asked in geometry and locus questions
- Helps visualise all possible positions under continuous rotation

































