To Determine the Equivalent Resistance of Resistors When Connected in Series and in Parallel

Physics-Experiment - Determination of the Equivalent Resistance of Resistors When Connected in Series - Introduction

When two resistors are connected in an end-to-end manner in a circuit then they are considered to be connected in the series. In a series combination, the flow of current is the same in both resistors, since the current always flows in one direction; however, the total voltage of the battery drops across the resistors depending on the value of their resistances. Therefore, in the household, the appliances connected in series sometimes fail due to the flow of an unexpectedly high current through the circuit and causing short circuits.

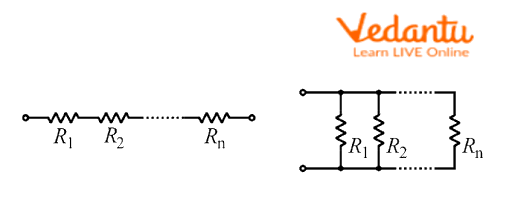
Series and Parallel combination of resistors

Table of Content

(a) Physics-Experiment - Determination of the Equivalent Resistance of Resistors When Connected in Series - Introduction

• Aim

• Theory

• Procedure 

• Observations

• Result

(b) To Determine the Equivalent Resistance of Resistors When Connected in Parallel

• Introduction

• Aim

• Theory

• Observations

• Result

• Precautions

Aim

Determination of equivalent resistance in a series combination of resistances.

Apparatus Required 

List of tools required to experiment:

• Connecting wires

• A 12 V Battery

• A plug key

• A Rheostat 

• An ammeter

• A voltmeter

• A piece of sandpaper

• Two resistors of different values

• Rheostat

Theory

The resistances connected in the series combination will have an equal amount of current; and the total voltage drop across the resistor will depend on the effective resistance of that resistor. Let's consider that there are two resistances of values \[{R_1}\;and\;{R_2}\] connected in a series combination. When a current of value \[I\] flows through this resistance, a voltage drop \[{V_1}\;and\;{V_2}\] occurs across them. Since the total voltage of the battery \[V\]is fixed, therefore, we can write,

\[V = {V_1} + {V_2}\]

According to Ohm’s law, the voltage drop across each resistor can be given as follows,

\[\begin{array}{l}{V_1} = I{R_1}\\{V_2} = I{R_2}\end{array}\]

Now substitute these values in the above expression, and we get,

\[V = I{R_1} + I{R_2}\]

Now, if we consider that the equivalent resistance of the circuit is \[R\], then the total voltage drop will be, \[V = IR\], and thus we can write the above expression as,

\[\begin{array}{l}V = IR = I{R_1} + I{R_2}\\R = {R_1} + {R_2}\end{array}\]

Thus, the equivalent resistance of a series circuit can be expressed as,

\[R = {R_1} + {R_2}\]

Procedure

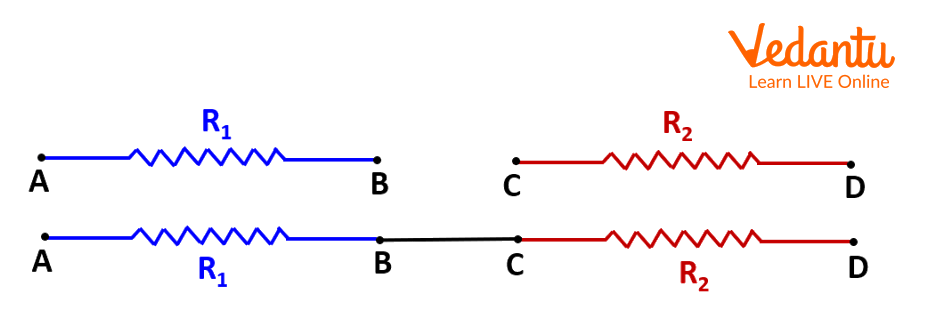
Series combination of resistors.

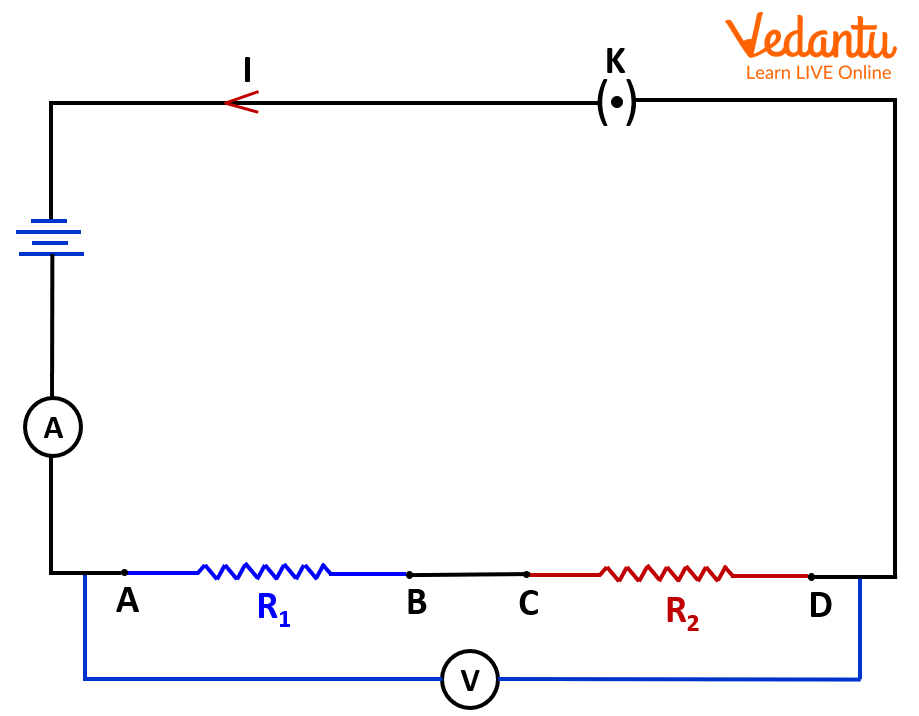
Circuit for series combination of two resistors AB and CD.

Please follow these steps one by one:

1. Make sure to check the zeros of the Ammeter and Voltmeters and note down the least counts of them. 

2. Clean the joining ends of the connecting wire to make sure the proper electric connections.

3. Do not insert the plug key.

4. Take two resistors of known resistance and connect them in a circuit as given in the image 2 and connect the other components, like, ammeter, voltmeter, key, battery, and others systematically.

5. Connect the two known resistors with a connecting wire at the ends B and C as shown in the Image 2.

6. Now, Insert the plug key in the circuit to allow the flow of current in the circuit and note down the readings of the ammeter and voltmeter across the A and D points of the circuit as shown in Image 2. Now, remove the plug key to avoid the excessive heating of the wires.

7. Repeat this experiment with the five different values of currents and note down the readings of a voltmeter and an ammeter in each case as recorded in the step 5 above. 

Observations 

Least Count of Ammeter = …. A

Range of Ammeter = …. A

Least Count of Voltmeter = …. V

Range of Voltmeter = …. V

Resistance of the first resistor = ….Ω

Resistance of the second resistor = ….Ω

Resistance of the first resistor = ….Ω

Resistance of the second resistor = ….Ω

Equivalent Resistance = ….Ω

Result

Now compare the experimentally obtained value of equivalent resistance with the calculated value of the equivalent resistance from the above equation. Write your observation here ____.

(b) To Determine the Equivalent Resistance of Resistors When Connected in Parallel

Introduction

When resistors are connected across each other in a circuit, then those resistors are considered to be connected in a parallel combination. In a parallel combination, the current flow is divided among the resistors, while the voltage drop across each resistor is the same, depending on the value of these individual resistors. Therefore, in the household wiring, all electric appliances are connected in a parallel combination to ensure an equal voltage to each of them, and, therefore, the undisturbed operation is maintained.

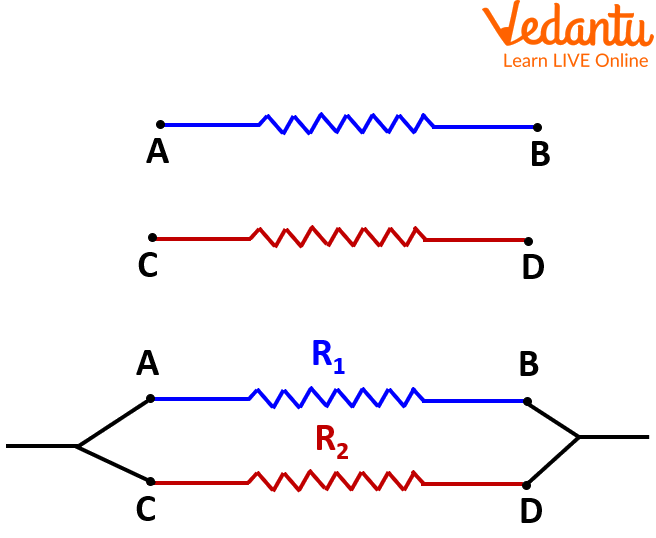
Parallel combination of resistors

Aim

Determination of equivalent resistance in a parallel combination of resistors.

Apparatus Required 

List of tools required to perform the experiment:

• Connecting wires

• A 12 V Battery

• A plug key

• A Rheostat 

• An ammeter

• A voltmeter

• A piece of sandpaper

• Two resistors of different values

• Rheostat

Theory

The resistors are connected in a parallel combination and will encounter an equal amount of voltage drop across each of them and the current will be divided among these resistors depending on their value. If we consider that the two resistors of values \[{R_1}\; and\;{R_2}\] are connected in a parallel combination, and both experience a voltage drop \[V\], when the current \[{i_1}\; and\;{i_2}\] flows through these resistors, respectively. Since the total current from the battery \[i\] is fixed, therefore, we can write,

\[i = {i_1} + {i_2}\]

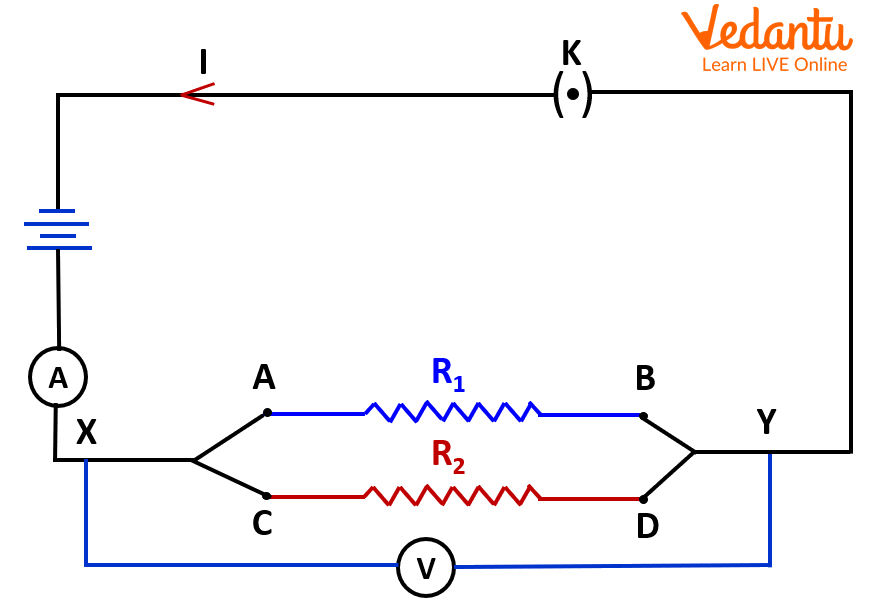
Circuit diagram for the Parallel combination.

According to Ohm’s law, the voltage drop across each resistor can be given as follows,

\[\begin{array}{l}{i_1} = \dfrac{V}{{{R_1}}}\\{i_2} = \dfrac{V}{{{R_2}}}\end{array}\]

Now substitute these values in the above expression, and we get,

\[i = \dfrac{V}{{{R_1}}} + \dfrac{V}{{{R_2}}}\]

Now, if we consider that the equivalent resistance of the circuit is \[R\], then the total voltage drop will be, \[V = IR\], and thus we can write the above expression as,

\[\begin{array}{l}\dfrac{V}{R} = \dfrac{V}{{{R_1}}} + \dfrac{V}{{{R_2}}}\\\dfrac{1}{R} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}\end{array}\]

Thus, the equivalent resistance of a series circuit can be expressed as,

\[\dfrac{1}{R} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}\]

Procedure

Please follow these steps one by one:

1. Make sure to check the zeros of the Ammeter and Voltmeters and note down the least counts of them. 

2. Clean the joining ends of the connecting wire to ensure the proper electric connections.

3. Do not insert the plug key.

4. Take two resistors of known resistance and connect them in a circuit as given in image 4 and connect the other components, like, the ammeter, voltmeter, key, battery, and others systematically.

5. Connect the two known resistors with a connecting wire at the ends A and C as well as B and D, as shown in the image 4.

6. Now, insert the plug key in the circuit to allow the flow of current in the circuit and note down the readings of the ammeter and voltmeter across the X and Y points of the circuit as shown in image 2. Now, remove the plug key to avoid the excessive heating of the wires.

7. Repeat this experiment with the five different values of currents and note down the readings of the voltmeter and an ammeter in each case as recorded in the step 5 above.

Observations 

Least Count of Ammeter = …. A

Range of Ammeter = …. A

Least Count of Voltmeter = …. V

Range of Voltmeter = …. V

Resistance of the first resistor = ….Ω

Resistance of the second resistor = ….Ω

Resistance of the first resistor = ….Ω

Resistance of the second resistor = ….Ω

Equivalent Resistance = ….Ω

Result

Now, compare the experimentally obtained value of equivalent resistance with the calculated value of the equivalent resistance from the above equation. Write your observation here____.

Precautions

• Please make sure that the connections are tight.

• Insert and remove the plug key as mentioned in the procedure.

• The voltmeter should always be connected parallel to the resistors.

• The ammeter should always be connected in series with the resistors.

• The least count of the voltmeter and ammeter should be determined properly.

• All connections should be made following the diagram.

• To avoid Joule heating, the current should flow when recording the readings.

Lab Manual Questions 

1. In what way should household appliances be connected??

Ans: In the household circuits to supply the equivalent voltage to each appliance, they are connected in a parallel combination. In addition, it ensures that the working of other electric appliances will remain unaffected if there is some issue with the other appliances.

2. Two resistors are connected in series and then in parallel. What effect will it have on the readings of the voltmeter and ammeter?  

Ans: Two resistors in a series combination will result in the same value of current and different readings of voltages when an ammeter and voltmeters are connected across them, respectively, while two resistors connected in parallel will give the same readings in a voltmeter and different readings in the ammeter when connected across them, respectively.

3. What will be the equivalent resistance for the \[5\;\Omega \;and\;10\;\Omega \] connected in parallel?

Ans: The equivalent resistance can be calculated as follows for the \[5\;\Omega \;and\;10\;\Omega \] resistors connected in parallel such that,

\[\begin{array}{l}\dfrac{1}{{{R_P}}} = \dfrac{1}{{5\;\Omega }} + \;\dfrac{1}{{10\;\Omega}}\\\dfrac{1}{{{R_P}}} = \dfrac{{2 + 1}}{{10\;\Omega }}\\{R_P} = \dfrac{{10}}{3}\;\Omega \end{array}\]

Thus, the equivalent resistance is \[{R_P} = \dfrac{{10}}{3}\;\Omega \].

4. What will be the equivalent resistance for the \[5\;\Omega \;and\;10\;\Omega \] connected in series?

Ans: The equivalent resistance can be calculated as follows for the \[5\;\Omega \;and\;10\;\Omega \] resistors connected in series such that,

\[\begin{array}{l}{R_S} = 5\;\Omega  + \;10\;\Omega \\{R_S} = 15\;\Omega \end{array}\]

Thus, the equivalent resistance is \[{R_S} = 15\;\Omega \].

Viva Questions

1. What is a voltmeter?

Ans: Voltmeter is an electric device utilized to measure the voltage across the electric component when connected parallel to it.

2. What is an ammeter?

Ans: An ammeter is an electric device utilized to measure the current flow along an electric component when connected in series to it.

3. What is the use of a rheostat?

Ans: The rheostat is used as a device of variable resistance in an electric circuit.

4. Name some wire materials that can be used for making electric connections?

Ans: Copper, Aluminium, Silver, Gold, etc.

5. What is Ohm’s law?

Ans: Ohm’s law states that the voltage is directly proportional to the electric current in the circuit; therefore, \[V = IR\]. 

6. What will happen to voltage if the current through a resistor is increased in a circuit? 

Ans: Since voltage is directly proportional to the current, therefore voltage will also increase with the current.

7. Why is the ammeter connected in the series?

Ans: The ammeter is connected in series; therefore, the same current flows through the ammeter and measures the same value of current passing through the electric circuit.

8. Why is the voltmeter connected to a parallel?

Ans: The voltmeter is connected to a parallel since it measures the total voltage drop across the electric component.

9. How can an ammeter be formed using a galvanometer?

Ans: An ammeter can be formed using a galvanometer if a resistance of a smaller value is connected parallel to it, so the total resistance will be very low and that makes it suitable to flow the current.

10. How can a voltmeter be formed using a galvanometer?

Ans: A voltmeter can be formed using a galvanometer if a resistance of a large value is connected in series to it, so the total resistance will be very high and that makes it suitable that there will be no leakage of current through it and drops the maximum voltage.

Practical-Based Resistors in Series and Parallel Problems and Solutions

1. When resistors are connected in series, what happens to the final resistance?

1. Decrease

2. Increase

3. No change

4. Infinite

Ans: B. Increase

2. Where should a voltmeter be connected in a circuit?

1. Parallel

2. Series

3. Between two resistors

4. Across switch

Ans: A. Parallel

3. Where should an ammeter be connected in a circuit?

1. Parallel

2. Series

3. Between two resistors

4. Across switch

Ans: B. Series

4. What will be the voltmeter reading across a \[2\;\Omega \] resistor that has a 1 A current?

1. 2 V

2. 0.5 V

3. 10 V

4. 1.2 V

Ans: A. 2 V

5. When resistors are connected in parallel, what happens to the final resistance?

1. Decrease

2. Increase

3. No change

4. Infinite

Ans: A. Decrease

6. What is the unit of voltage?

1. \[\Omega \]

2. unitless

3. V

4. A

Ans: C. V

7. What is the unit of current?

1. \[\Omega \]

2. unitless

3. V

4. A

Ans: D. A

8. What is the unit of resistance?

1. \[\Omega \]

2. unitless

3. V

4. A

Ans: A. \[\Omega \]

9. What is the use of a key in an electric circuit?

1. Connect the circuit

2. Disconnect the circuit

3. Increase Current

4. Decrease Current

Ans: A. Connect the circuit

10. Which formula is used for the equivalent resistance of two resistors in series?

1. \[\dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}\]

2. \[{R_1} + {R_2}\]

3. \[{R_1} - {R_2}\]

4. \[{R_1}/{R_2}\]

Ans: B. \[{R_1} + {R_2}\]

Conclusion

From this experiment, one can conclude that the combination of resistors in parallel or series combination decreases and increases, respectively. In the series combination, the voltage is divided among resistors, and the same current flows through the resistors. In a parallel combination, current divides among the resistors, and the voltage remains the same. Therefore, a desired value of the resistance can be obtained from a series of parallel combinations of resistors.