
Class 7 Maths NCERT Exemplar Solutions Chapter 1- Integers
Free PDF download of NCERT Exemplar for Class 7 Maths Chapter 1 - Integers solved by expert Maths teachers on Vedantu.com as per NCERT (CBSE) Book guidelines. All Chapter 1 - Integers exercise questions with solutions to help you to revise the complete syllabus and score more marks in your examinations.
Every NCERT Solution is provided to make the study simple and interesting on Vedantu. Subjects like Science, Maths, English will become easy to study if you have access to NCERT Solution for Class 7 Science, Maths solutions and solutions of other subjects. You can also download NCERT Solutions for Class 7 Maths to help you to revise the complete syllabus and score more marks in your examinations.
NCERT Exemplar for Class 7 Maths Solutions Chapter 1 Integers
Access NCERT Exemplar Solutions for Class 7 Mathematics
Chapter 1 - Integers
(Examples, Easy Methods and Step by Step Solutions)
Solved examples:
1. Madhre is standing in the middle of a bridge which is 20 m above the water level of a river. If a 35 m deep river is flowing under the bridge (see figure), then the vertical distance between the foot of Madhre and bottom level of the river is:
(a) 55 m
(b) 35 m
(c) 20 m
(d) 15 m
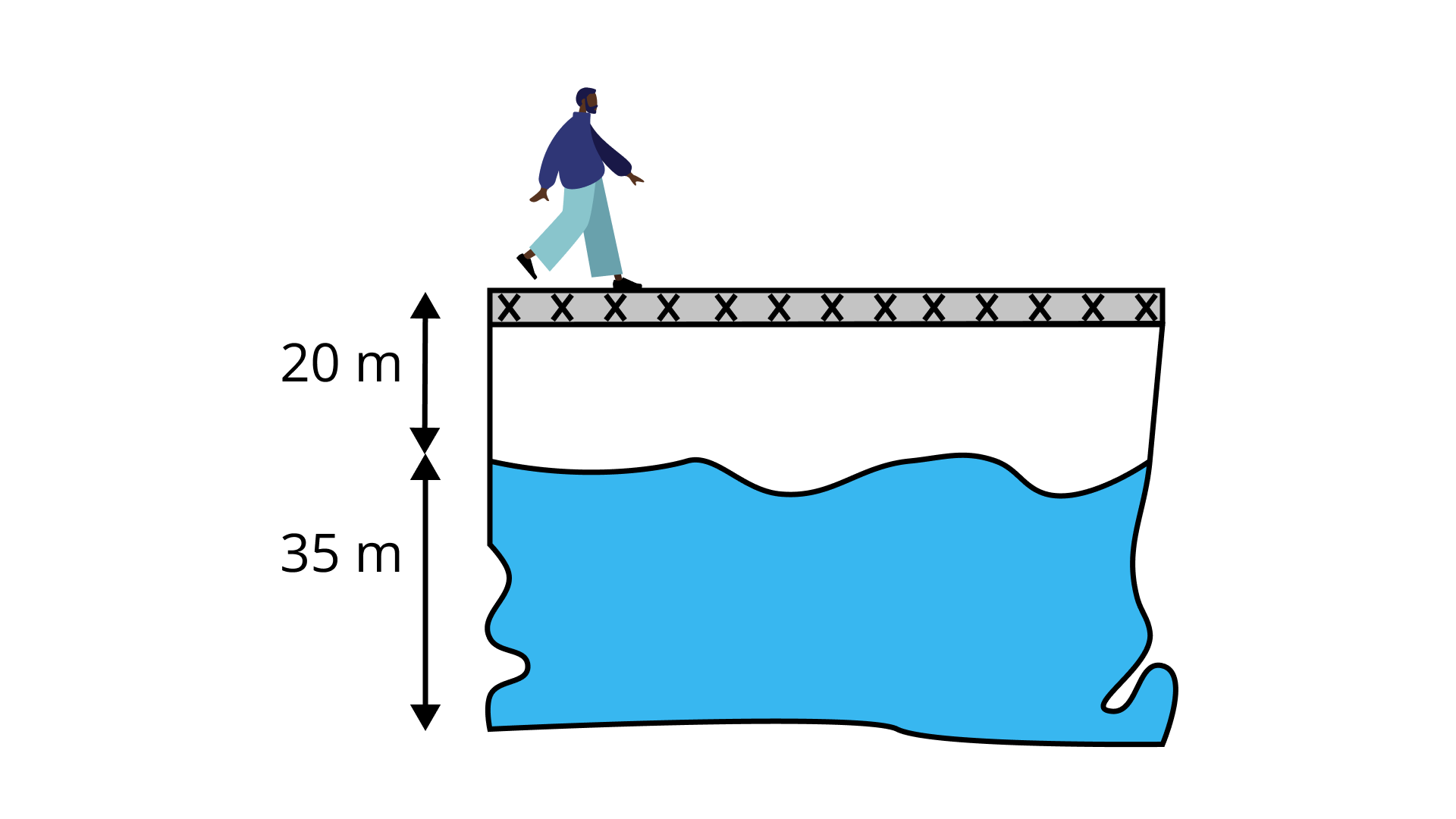
Ans: The correct answer is (a).
Vertical distance $= 20 m + 35 m = 55 m$
2. $\text{[(– 10) × (+ 9)] + (–10)}$ is equal to
(a) 100
(b) –100
(c) – 80
(d) 80
Ans: Correct answer is (b)
$\text{[(– 10) × (+ 9)] + (–10)}$
$= – 90 – 10$
$= – 100$
3. $–16 \div \text{[}8 \div (–2)\text{]}$ is equal to
(a) –1
(b) 1
(c) 4
(d) –4
Ans: Correct answer is (c),
$- 16 \div \left[ {8 \div \left( { - 2} \right)} \right] = - 16 \div \left[ {\dfrac{8}{{ - 2}}} \right]$
$= - 16 \div \left[ { - 4} \right]$
$=\dfrac{{ - 16}}{{ - 4}}$
$= 4$
In questions 4 and 5, fill in the blanks to make the statements true.
4. (– 25) $\times$ 30 = – 30 $\times$ _______.
Ans: 25
$(– 25) \times 30 = – 30 \times 25$
5. $75 ÷ _______ = – 75$
Ans: – 1
\[75 \div \left( { - 1} \right) = - 75\]
In questions 6 and 7, state whether the statements are True or False.
6. $(–5) \times (–7)$ is same as $(–7) \times (–5)$
Ans: True
$(–5) \times (–7) = 35$
$(–7) \times (–5) = 35$
7. $(– 80) \div (4)$ is not same as $80 \div (–4)$
Ans: False
$\left( { - 80} \right) \div \left( 4 \right) = \dfrac{{ - 80}}{4} = - 20$
$80 \div \left( { - 4} \right) = \dfrac{{80}}{{ - 4}} = - 20$
So, both are the same.
8. Find the odd one out of the four options in the following:
(a) (–2, 24)
(b) (–3, 10)
(c) (–4, 12)
(d) (–6, 8)
Ans: Odd one is (b).
Here $– 2 \times 24 = – 48$,
$– 4 \times 12 = – 48$ and
$– 6 \times 8 = – 48$
All the pairs i.e. (–2, 24); (–4, 12); (–6, 8) give the same answer on multiplication, whereas –3 × 10 = –30, gives a different answer.
9. Find the odd one out of the four options given below:
(a) (–3, –6)
(b) (+1, –10)
(c) (–2, –7)
(d) (–4, –9)
Ans: Odd one out is (d).
Here –3 + (–6) = –9,
+1 + (–10) = –9 and
–2 + (–7) = –9
All the above pairs i.e. (–3, –6); (+1, –10); (–2, –7) give the same answer on adding, whereas – 4 + (–9) = –13, gives a different answer.
10. Match the integer in column I to an integer in column II so that the sum is between –11 and – 4.
Column I | Column II |
(a) –6 | (i) –11 |
(b) +1 | (ii) –5 |
(c) +7 | (iii) +1 |
(d) –2 | (iv) –13 |
Ans: (a) ↔ (iii)
As –6 + (+1) = –5, which lies between –11 and –4.
(b) ↔ (i)
As +1 + (–11) = –10 which lies between –11 and –4.
(c) ↔ (iv)
As +7 + (–13) = –6 which lies between –11 and –4.
(d) ↔ (ii)
As –2 + (–5) = –7 which lies between –11 and –4.
11. If a is an integer other than 1 and –1, match the following:
Column I | Column II |
(a) $a ÷ (–1)$ | (i) a |
(b) $1 ÷ (a)$ | (ii) 1 |
(c) $(–a) ÷ (–a)$ | (iii) Not an integer |
(d) $a ÷ (+1)$ | (iv) –a |
Ans: (a) ↔ (iv)
$a \div \left( { - 1} \right) = \dfrac{a}{{ - 1}} = - a$
(b) ↔ (iii)
$1 \div a = \dfrac{1}{a}$
Since a is an integer, $\dfrac{1}{a}$ will not be an integer.
(c) ↔ (ii)
$\left( { - a} \right) \div \left( { - a} \right) = \dfrac{{ - a}}{{ - a}} = 1$
(d) ↔ (i)
$\dfrac{a}{{ + 1}} = a$
12. Write a pair of integers whose sum is zero (0) but the difference is 10.
Ans: Since the sum of two integers is zero, one integer is the additive inverse of another integer, like – 3, 3; – 4, 4 etc.
But the difference has to be 10. So, the integers are 5 and – 5 as $5 – (–5)$ is 10.
13. Write two integers which are smaller than –3, but their difference is greater than –3.
Ans: – 5 and – 4 are smaller than – 3 but their difference is $(–4) – (–5) = 1$ which is greater than – 3.
Or
– 6 and –10 are smaller than – 3 but their difference is $(–6) – (–10) = 4$ which is greater than – 3.
14. Write a pair of integers whose product is – 15 and whose difference is 8.
Ans: There are few pairs of integers whose product is – 15.
e.g.$ – 1 × 15$
$– 3 × 5$
$3 × (– 5)$
$15 × (– 1)$
but the difference between –3 and 5 or –5 and 3 is 8. So, the required pair of integers is $– 3, 5$ and $– 5, 3$.
15. If $∆$ is an operation such that for integers a and b we have $a ∆ b = a × a + b × b – a × b$, then find $(–3) ∆ 2.$
Ans: $–3 ∆ 2 = (–3) × (–3) + 2 × 2 – (–3) × 2$
$= 9 + 4 – (– 6) = 13 + 6 = 19.$
16: In an objective type test containing 25 questions. A student is to be awarded +5 marks for every correct answer, –5 for every incorrect answer and zero for not writing any answer. Mention the ways of scoring 110 marks by a student.
Ans: Marks scored = +110
So, minimum correct responses $= 110 ÷ (+5) = 22$
Case 1.
Correct responses = 22
Marks for 1 correct response = + 5
Marks for 22 correct response $= +110$ (As 22 × 5 = 110)
Marks scored = +110
Marks obtained for incorrect answer = 0
So, no incorrect response
And, therefore, 3 were un-attempted
Case 2.
Correct responses = 23
Marks from 23 correct responses = + 115 (As 23 × 5 = 115)
Marks scored = + 110
Marks obtained for incorrect answers = 110 – (+115)
= –5
Marks for 1 incorrect answer = –5
Number of incorrect responses = (–5) ÷ (–5)
= 1
So, 23 correct, 1 incorrect and 1 un-attempted.
Case 3.
Correct responses = 24
Marks from 24 correct responses = + 120 (As 24 × 5 = 120)
Marks scored = + 110
Marks obtained for incorrect answers = +110 – (+120)
= –10
Number of incorrect responses = (–10) ÷ (–5)
= 2
Thus, the number of questions = 24 + 2 = 26. Whereas, the total number of questions is 25. So, this case is not possible.
So, the possible ways are:
• 22 correct, 0 incorrect, 3 un-attempted.
• 23 correct, 1 incorrect, 1 un-attempted.
17. A boy standing on the third stair goes up five more stairs. Which stair is he standing at now? At which step will he be after he comes down 2 stairs?
Ans: He is currently at the third stair i.e. at (+3).
• He goes up 5 stairs in the same direction.
• Since 3 + 5 = 8. Therefore, he is at the 8th stair on the staircase.
Now, the boy comes down 2 stairs. Since he comes down in the opposite direction i.e. downwards by 2 stairs (i.e. –2), so 8 + (–2) = 8 – 2 = 6.
Therefore, he is at 6th step now.
Exercise
1. When the integers 10, 0, 5, -5, -7 are arranged in descending or ascending order, then find out which of the following integers always remains in the middle of the arrangement.
(a) 0
(b) 5
(c) –7
(d) –5
Ans: Option (a) is correct.
The integers are 10, 0, 5, -5, -7
Descending order: 10, 5, 0, – 5, – 7
Ascending order: -7, – 5, 0, 5, 10
Thus, 0 is the integer which always remains in the middle of the arrangement.
2. By observing the number line, state which of the following statements is not true?
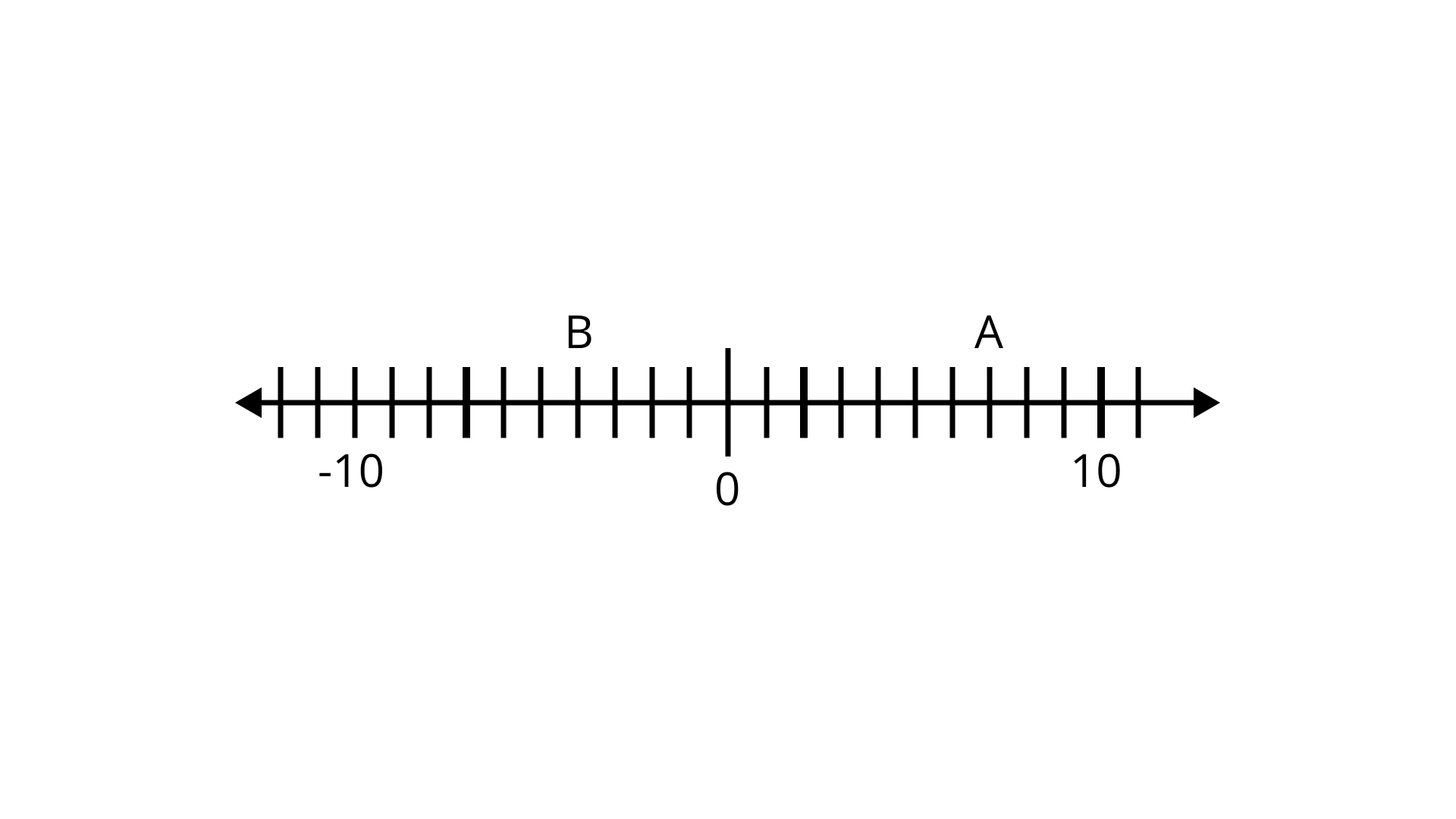
(a) B is greater than -10
(b) A is greater than 0
(c) B is greater than A
(d) B is smaller than 0
Ans: Option (d) is correct.
Since B is on the left side of the number line to A, B is smaller than A.
3. By observing the number line, state which of the following statements is true?

(a) B is 2
(b) A is – 4
(c) B is -13
(d) B is – 4
Ans: Option (d) is correct.
Here, A is 7 and B is -4.
4. Next three consecutive numbers in the pattern 11, 8, 5, 2,______ ,__ ,__ are
(a) 0, – 3, – 6
(b)-1,-5,-8
(c) – 2, — 5, – 8
(d) -1,-4,-7
Ans: Option (d) is correct.
Here, the pattern is
11 – 3 = 8, 8 – 3 = 5, 5 – 3 = 2
So, the next three consecutive numbers will be 2 – 3 = -1, -1 – 3 = – 4, -4 – 3 = – 7
i.e., -1, -4, -7.
5. The next number in the pattern – 62,- 37,- 12 is_________________ .
(a) 25
(b) 13
(c) 0
(d) -13
Ans: Option (b) is correct.
Here, the pattern is -62 + 25 = -37, -37 + 25 = -12
So, next number in the pattern will be -12 + 25 = 13
6. Which of the following statements is not true?
(a) When two positive integers are added, we always get a positive integer.
(b) When two negative integers are added, we always get a negative integer.
(c) When a positive integer and a negative integer are added, we always get a negative integer.
(d) Additive inverse of an integer 2 is (-2) and additive inverse of (-2) is 2.
Ans: Option (c) is correct.
Statement (c) is false because when a positive integer and a negative integer is added we may also get a positive integer or zero. For example, -2 + 2 = 0 and -4 + 5 = 1.
7. On the following number line value, ‘zero’ is shown by the point
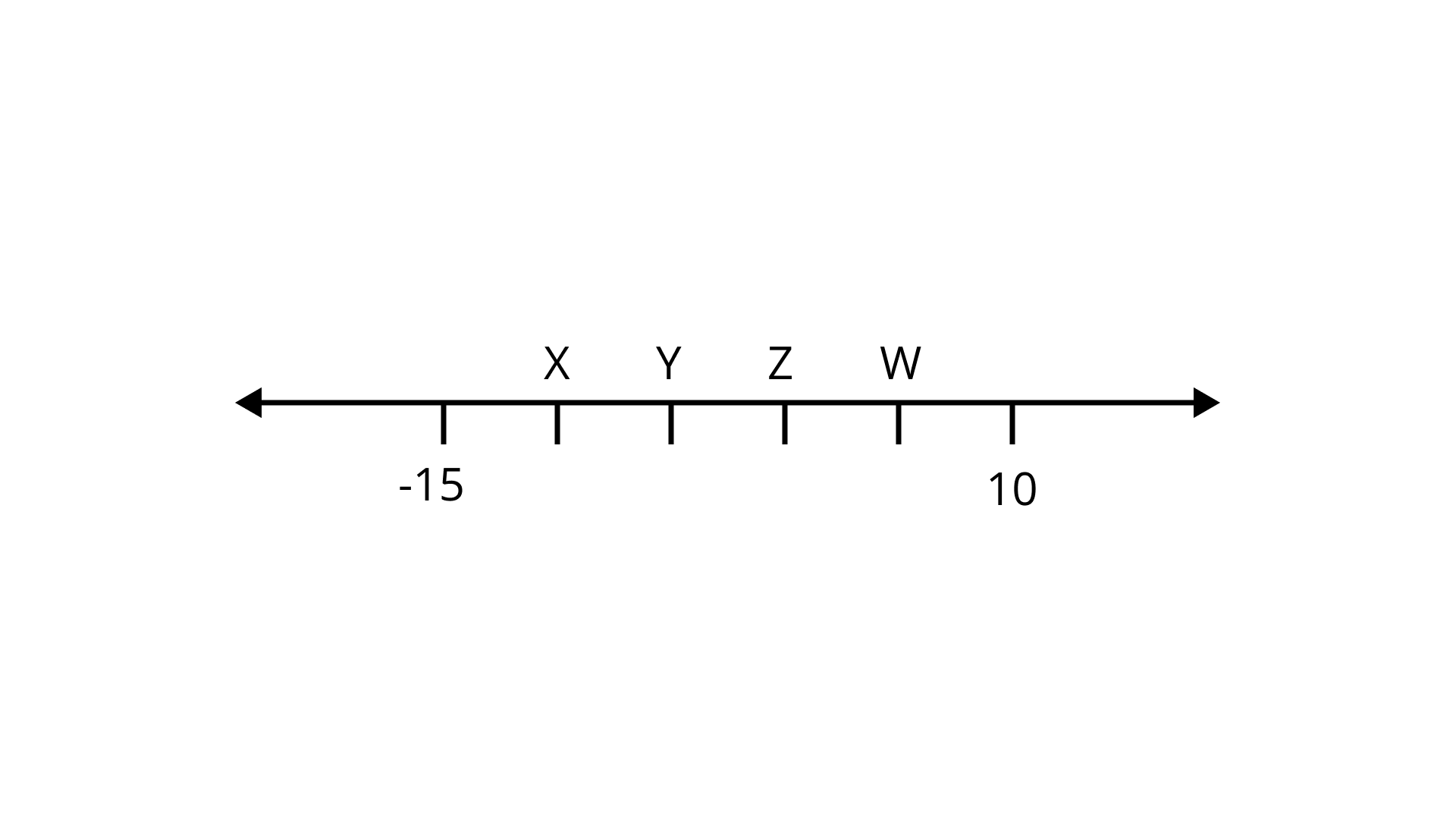
(a) X
(b) Y
(c) Z
(d) W
Ans: Option (c) is correct.
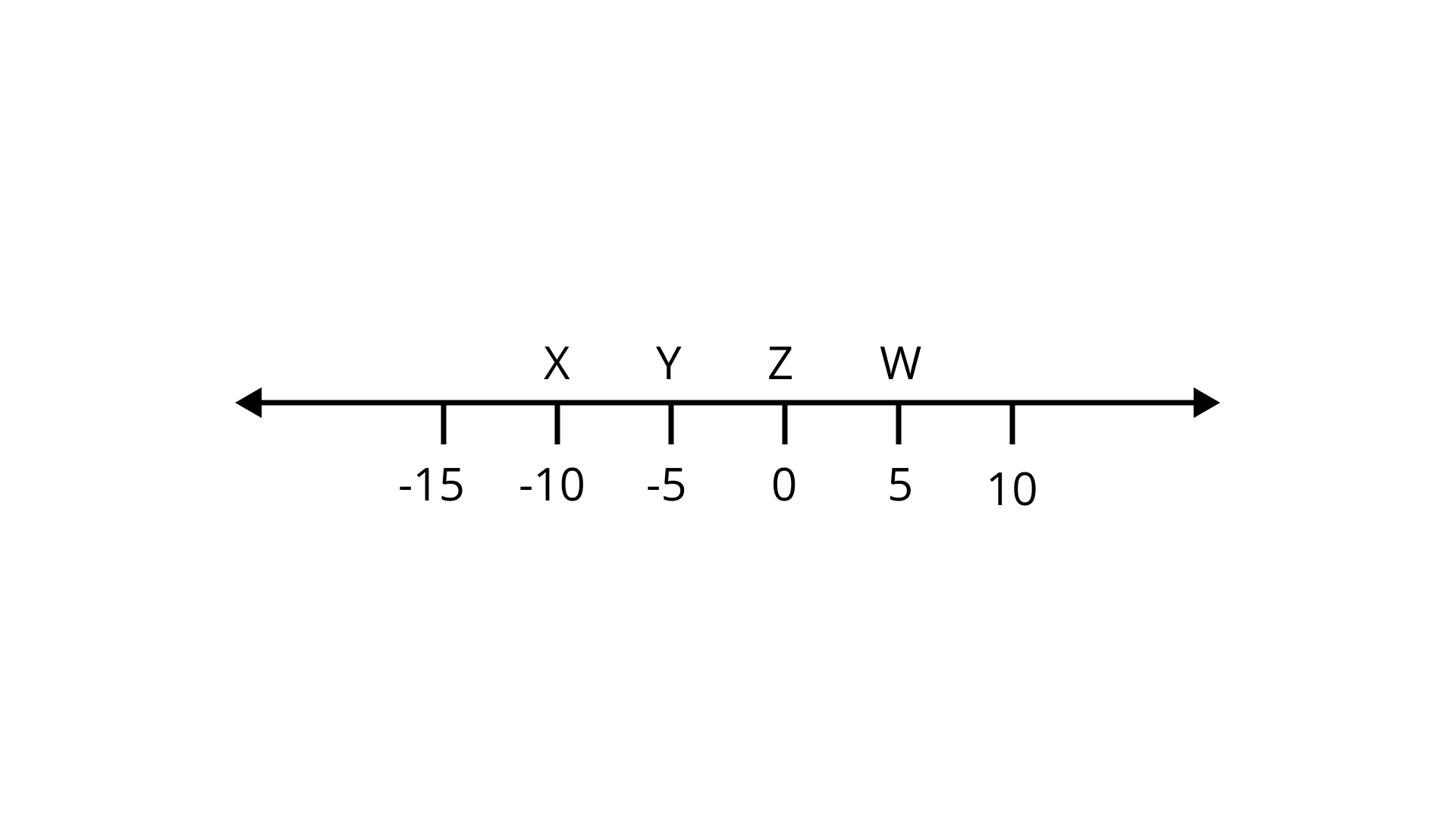
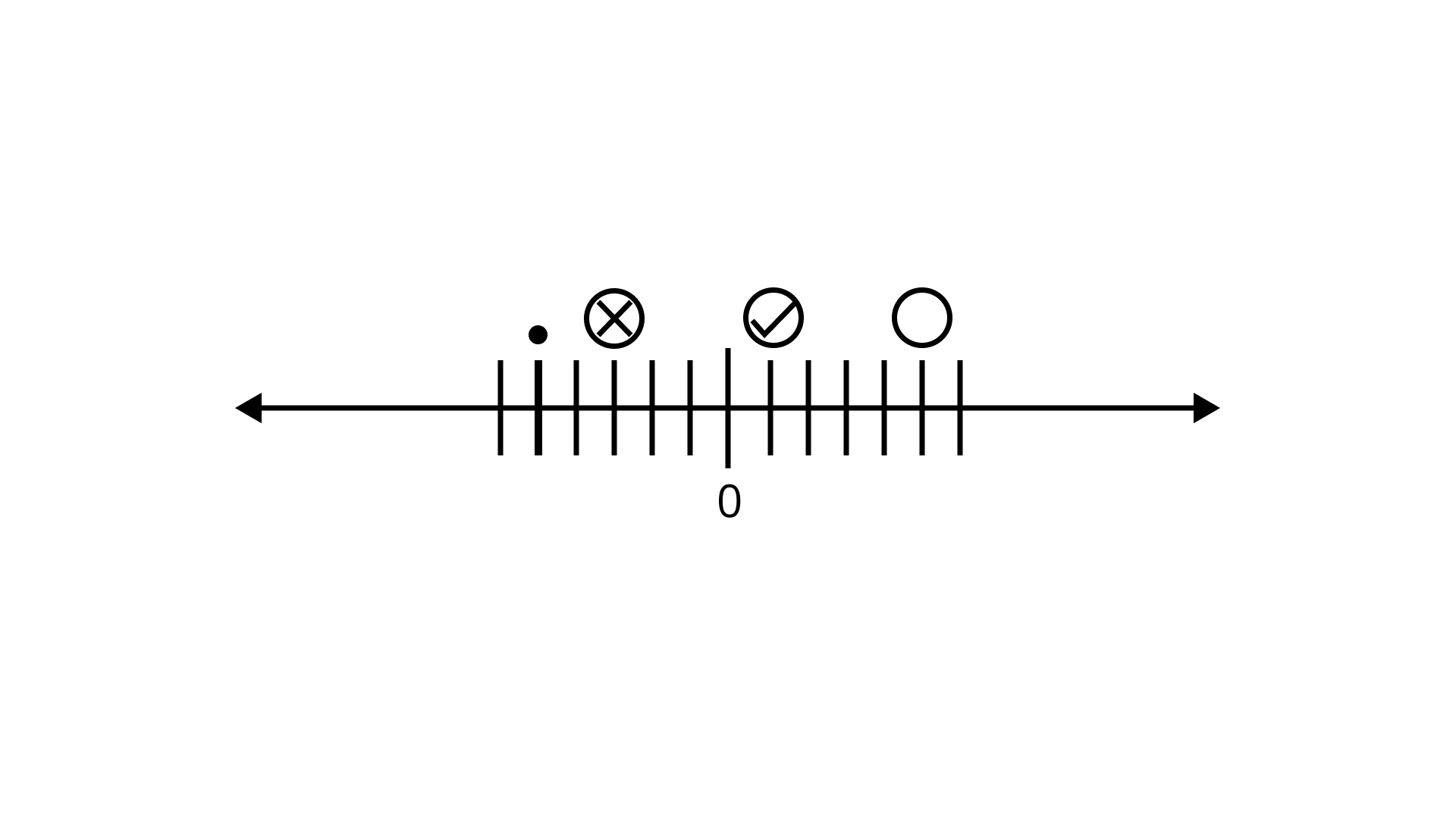
8. If these following represent some integers on number line
Then descending order of these numbers is
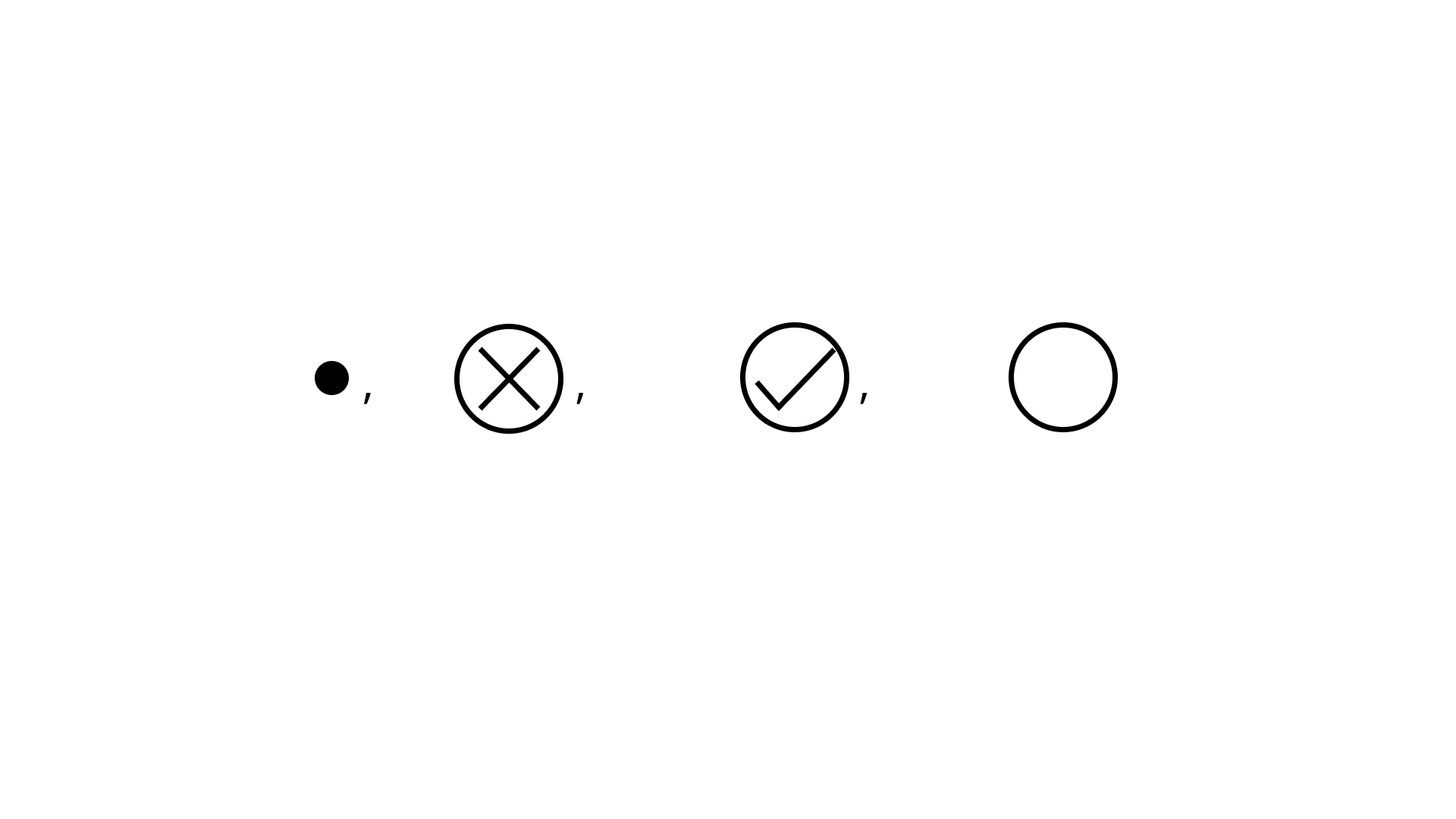
(a)
(b)
(c)
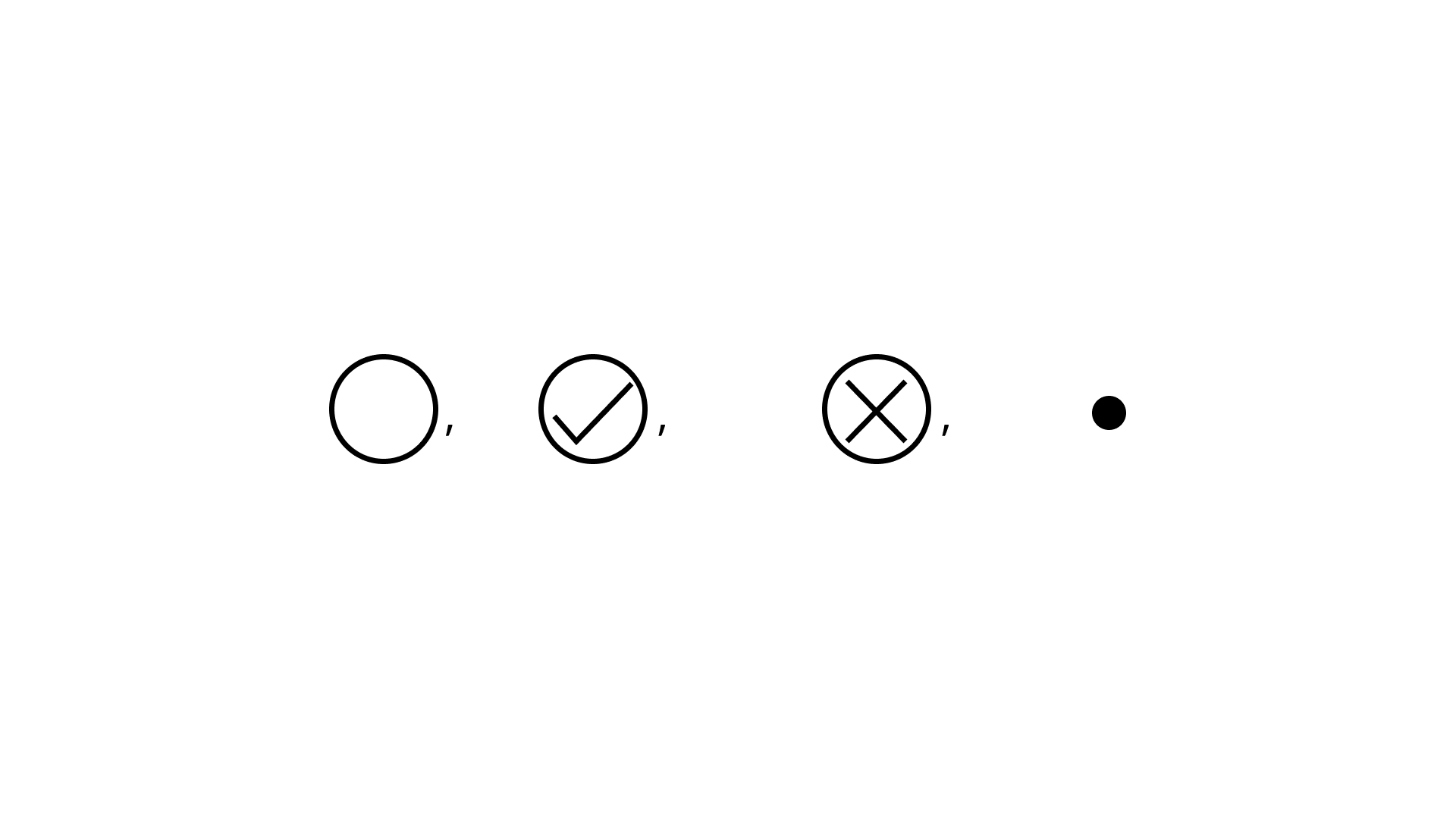
(d)
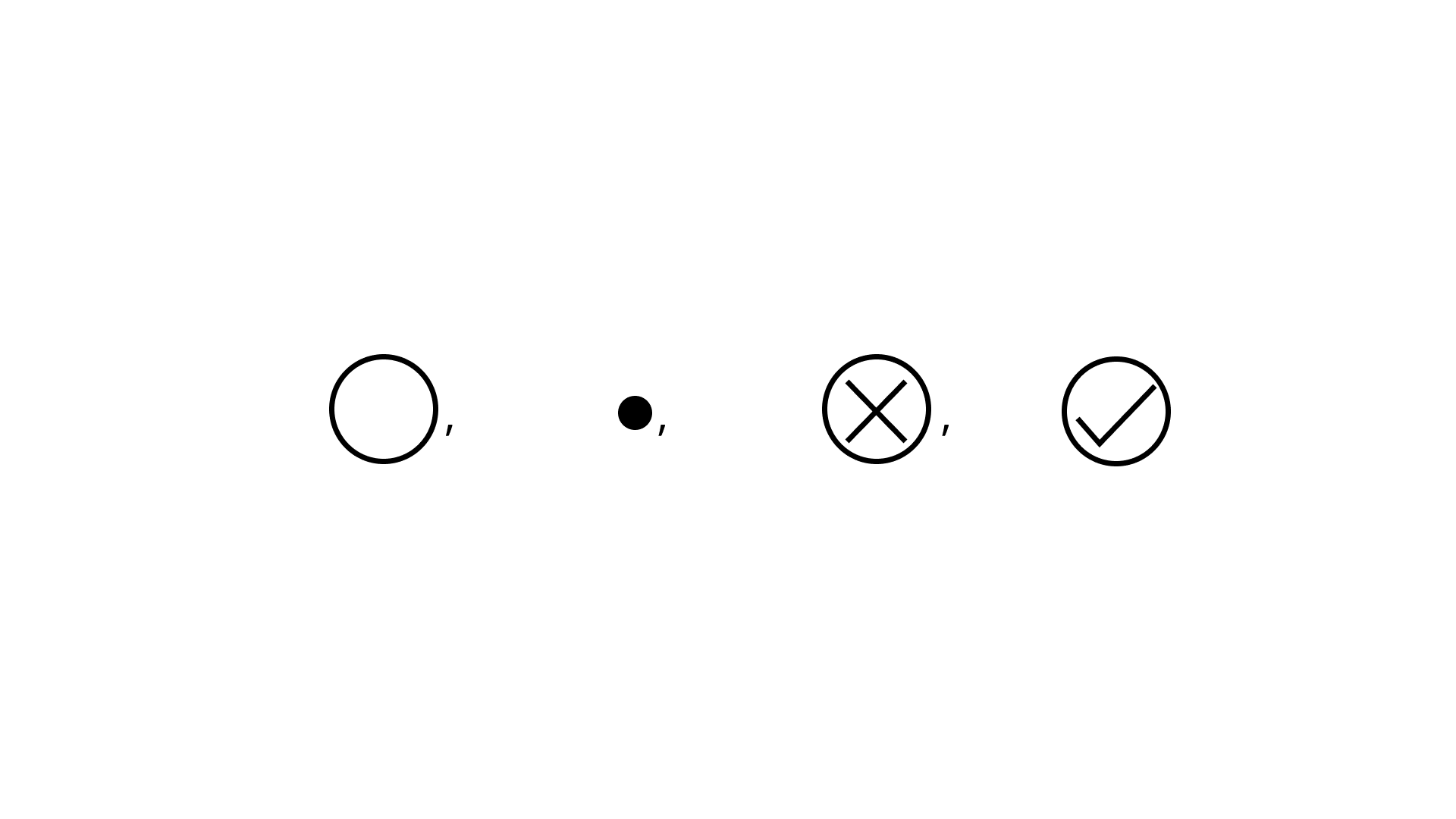
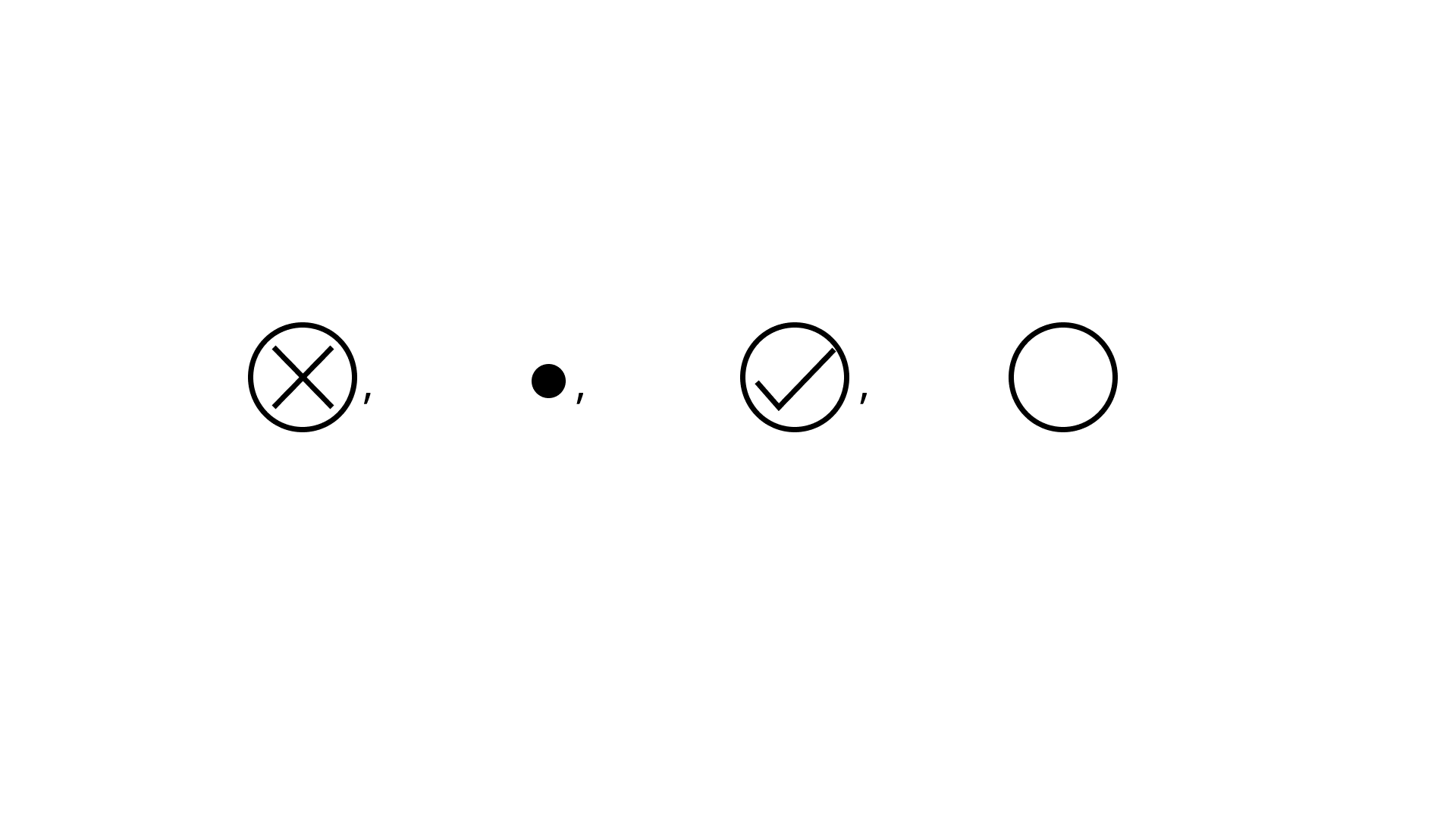
Ans: Option (c) is correct.
Descending order of given numbers is
9. On the number line, the value of (-3) x 3 lies on right hand side of
(a) -10
(b) – 4
(c) 0
(d) 9
Ans: Option (a) is correct.
Since, (-3) × 3 = – 9
It lies on right hand side of -10.
10. The value of $5 ÷ (- 1)$ does not lie between
(a) 0 and -10
(b) 0 and 10
(c) – 4 and -15
(d) – 6 and 6
Ans: Option (b) is correct.
The value of $5÷(−1) = −5$
Hence, -5 does not lie between 0 and 10.
11. Water level in a well was 20 m below ground level. During the rainy season, rainwater collected in different water tanks is drained into the well and the water level rises 5 m above the previous level. The wall of the well is 1 m 20cm high and a pulley is fixed at a height of 80 cm. Raghu wants to draw water from the well. The minimum length of the rope, that he can use is

(a) 17 m
(b) 18 m
(c) 96 m
(d) 97 m
Ans: Option (a) is correct.
Height of the wall of the well = 1 m 20 cm = 1.20 m
Height of the pulley = 80 cm = 0.80 m
So, required minimum length of the rope = (20 – 5 + 1.20 + 0.80) m
= (15 + 2) m = 17 m
Therefore, the minimum length of the rope is 17 m.
12. (-11) × 7 is not equal to
(a) 11 × (-7)
(b) -(11 × 7)
(c) (- 11) × (- 7)
(d) 7 × (-11)
Ans: Option (c) is correct.
(-11) × 7 = – (11 × 7)
= 11 × (-7) = 7 × (-11) = -77
But (-11) × 7 ≠ (-11) × (-7) {As (-11) × (-7) = 77}
13. (- 10) × (- 5) + (- 7) is equal to
(a) -57
(b) 57
(c) -43
(d) 43
Ans: Option (d) is correct.
(-10) × (- 5) + (- 7) = 50 + (-7) = 50 – 7 = 43
14. Which of the following is not the additive inverse of a?
(a) – (-a)
(b) a × (-1)
(c) – a
(d) a ÷ (-1)
Ans: Option (a) is correct.
Additive inverse of a is (- a).
So, option (b), (c) and (d) equals to -a. Now since –(-a) = a which cannot be the additive inverse of a.
15. Which of the following is the multiplicative identity for an integer a?
(a) a
(b) 1
(c) 0
(d) -1
Ans: Option (b) is correct.
Multiplicative identity for an integer a is 1. { As a × 1 = a = 1 × a}
16. $\left[(- 8) × (- 3)\right] × (- 4)$ is not equal to
(a) (- 8) × $\left[(- 3) × (- 4)\right] $
(b) $\left[(- 8) × (- 4)\right] $ × (- 3)
(c) $\left[(- 3) × (- 8)\right] $ × (- 4)
(d) (- 8) × (- 3) – (- 8) × (- 4)
Ans: Option (d) is correct.
$\left[(-8) × (-3)\right] $ × (-4) = (-8) × $\left[(-3) × (-4)\right] $
= $\left[(-8) × (-4)\right] $ × (-3)
= $\left[(-3) × (-8)\right] $ × (-4)
But
$\left[(-8) × (-3)\right] $ × (-4) ≠ (-8) ×(-3) – (-8) × (-4)
17. (- 25) × $\left[6 + 4\right]$ is not same as
(a) (-25) × 10
(b) (-25) × 6 + (- 25) × 4
(c) -25 × 6 × 4
(d) – 250
Ans: Option (c) is correct.
(- 25) × $\left[6 + 4\right] $= (-25) × 10
= -250
(- 25) × $\left[6 + 4\right] $= (-25) × 6 + (- 25) × 4
But (- 25) × $\left[6 + 4\right] $ ≠ (- 25) × 6 × 4
18. – 35 × 107 is not same as
(a) – 35 × (100 + 7)
(b) (- 35) × 7 + (- 35) × 100
(c) – 35 × 7 + 100
(d) (-30 -5) × 107
Ans: Option (c) is correct.
– 35 × 107 = – 35 × (100 + 7)
= (- 35) × 7 + (- 35) × 100
= (-30 -5) × 107
But – 35 × 107 ≠ -35 × 7 + 100
19. (- 43) × (- 99) + 43 is equal to
(a) 4300
(b) – 4300
(c) 425
(d) -4214
Ans: Option (a) is correct.
(- 43) × (- 99) + 43 = 43× 99 + 43
= 4257 + 43 = 4300
20. $(- 16) ÷ 4$ is not same as
(a) $(-4) ÷ 16$
(b) $-(16 ÷ 4)$
(c) $16 ÷ (-4)$
(d) – 4
Ans: Option (a) is correct.
$\left( { - 16} \right) \div 4 = \dfrac{{ - 16}}{4} = - 4$
But $\left( { - 4} \right) \div 16 = \dfrac{{ - 4}}{{16}} = \dfrac{{ - 1}}{4}$
So, $(-16) ÷ 4$ is not same as $(-4) ÷ 16.$
21. Which of the following does not represent an integer?
(a) 0 ÷ (- 7)
(b) 20 ÷ (- 4)
(c) (-9) ÷ 3
(d) (-12) ÷ 5
Ans: Option (d) is correct.
(a) 0 ÷ (-7) = 0
(b) 20 ÷ (- 4) = -5
(c) (-9) ÷ 3 = -3
(d) (−12) ÷ 5 = $\dfrac{{ - 12}}{5}$
Hence, (-12) ÷ 5 does not represent an integer.
22. Which of the following is different from the others?
(a) 20 + (-25)
(b) (-37) – (-32)
(c) (-5) × (-1)
(d) 45 ÷ (- 9)
Ans: Option (c) is correct.
(a) 20 + (- 25) = 20 – 25 = – 5
(b) (- 37) – (- 32) = – 37 + 32 = – 5
(c) (- 5) × (- 1) = 5
(d) (45) ÷ (−9) = −5
Hence, (-5) × (-1) is different.
23. Which of the following shows the maximum rise in temperature?
(a) 23° to 32°
(b) -10° to 1°
(c) -18° to-11°
(d) -5° to 5°
Ans: Option (b) is correct.
Rise in temperature,
(a) 32° – 23° = 9°
(b) 1°- (-10)° = 1° + 10° = 11° (maximum)
(c) -11°- (-18)° = -11° + 18° = 7°
(d) 5° – (-5°) = 5° + 5° = 10°
Hence, the maximum rise in temperature -10° to +1°.
24. If a and b are two integers, then which of the following may not be an integer?
(a) a + b
(b) a – b
(c) a × b
(d) a ÷ b
Ans: Option (d) is correct.
If a and b are two integers, then
a + b is always an integer.
a – bis always an integer.
a × b is also an integer,
but a ÷ b may or may not be an integer.
25. For a non-zero integer a, which of the following is not defined?
(a) a ÷ 0
(b) 0 ÷ a
(c) a ÷1
(d) 1 ÷ a
Ans: Option (a) is correct.
\[{\text{a}} \div 0 = \dfrac{{\text{a}}}{0}\] which is not defined.
Directions: Encircle the odd one of the following: (questions 26 to 30)
26.
(a) (-3, 3)
(b) (-5, 5)
(c) (-6, 1)
(d) (-8, 8)
Ans: Option (c) is correct.
(a) -3 + 3 = 0
(b) -5 + 5 = 0
(c) -6 + 1 = -5
(d) -8 + 8 = 0
So, (-6,1) is different.
27.
(a) (-1, -2)
(b) (-5, 2)
(c) (- 4, 1)
(d) (- 9, 7)
Ans: Option (d) is correct.
(a) -1 – 2 = -3
(b) -5 + 2 = -3
(c) -4 + 1 = -3
(d) -9 + 7 = -2
So, (-9, +7) is different.
28.
(a) (- 9) × 5 × 6 × (- 3)
(b) 9 × (-5) × 6 × (-3)
(c) (- 9) × (- 5) × (- 6) × 3
(d) 9 × (- 5) × (- 6) × 3
Ans: Option (c) is correct.
(a) (- 9) × 5 × 6 × (- 3) = 810
(b) 9 × (-5) × 6 × (-3) = 810
(c) (- 9) × (- 5) × (- 6) × 3 = -810
(d) 9 × (- 5) × (- 6) × 3 = 810
So, (- 9) × (- 5) × (- 6) × 3 is different.
29.
(a) (-100) ÷ 5
(b) (-81) ÷ 9
(c) (- 75) ÷ 5
(d) (-32) ÷ 9
Ans: Option (d) is correct.
(a) $\left( { - 100} \right) \div 5 = \dfrac{{ - 100}}{5} = - 20$
(b) $\left( { - 81} \right) \div 9 = \dfrac{{ - 81}}{9} = - 9$
(c) $\left( { - 75} \right) \div 5 = \dfrac{{ - 75}}{5} = - 15$
(d) $\left( { - 32} \right) \div 9 = \dfrac{{ - 32}}{9}$
Here, -20, -9, -15 all are integers $\dfrac{{ - 32}}{9}$ is not an integer.
30.
(a) \[\left( { - {\text{ }}{\mathbf{1}}} \right){\text{ }} \times {\text{ }}\left( { - {\text{ }}{\mathbf{1}}} \right)\]
(b) \[\left( { - {\text{ }}{\mathbf{1}}} \right){\text{ }} \times {\text{ }}\left( { - {\text{ }}{\mathbf{1}}} \right) \times {\text{ }}\left( { - {\text{ }}{\mathbf{1}}} \right)\]
(c) \[\left( { - {\text{ }}{\mathbf{1}}} \right){\text{ }} \times {\text{ }}\left( { - {\text{ }}{\mathbf{1}}} \right) \times {\text{ }}\left( { - {\text{ }}{\mathbf{1}}} \right) \times {\text{ }}\left( { - {\text{ }}{\mathbf{1}}} \right)\]
(d) \[\left( { - {\text{ }}{\mathbf{1}}} \right){\text{ }} \times {\text{ }}\left( { - {\text{ }}{\mathbf{1}}} \right) \times {\text{ }}\left( { - {\text{ }}{\mathbf{1}}} \right) \times {\text{ }}\left( { - {\text{ }}{\mathbf{1}}} \right) \times {\text{ }}\left( { - {\text{ }}{\mathbf{1}}} \right) \times {\text{ }}\left( { - {\text{ }}{\mathbf{1}}} \right)\]
Ans: Option (b) is correct.
$\left( {\text{a}} \right){\text{ }}\left( { - 1} \right){\text{ }} \times {\text{ }}\left( { - 1} \right){\text{ }} = {\text{ }}1$
$\left( {\text{b}} \right){\text{ }}\left( { - 1} \right){\text{ }} \times {\text{ }}\left( { - 1} \right){\text{ }} \times {\text{ }}\left( { - 1} \right){\text{ }} = {\text{ }} - 1$
$\left( {\text{c}} \right){\text{ }}\left( { - 1} \right){\text{ }} \times {\text{ }}\left( { - 1} \right){\text{ }} \times {\text{ }}\left( { - 1} \right){\text{ }} \times {\text{ }}\left( { - 1} \right){\text{ }} = {\text{ }}1$
$\left( {\text{d}} \right){\text{ }}\left( { - 1} \right){\text{ }} \times {\text{ }}\left( { - 1} \right){\text{ }} \times {\text{ }}\left( { - 1} \right){\text{ }} \times {\text{ }}\left( { - 1} \right){\text{ }} \times {\text{ }}\left( { - 1} \right){\text{ }} \times {\text{ }}\left( { - 1} \right){\text{ }} = {\text{ }}1$
So, \[\left( { - 1} \right){\text{ }} \times {\text{ }}\left( { - 1} \right){\text{ }} \times {\text{ }}\left( { - 1} \right)\] is different.
Directions: In s 31 to 71, fill in the blanks to make the statements true.
31. (- a) + b = b + additive inverse of ___.
Ans: a
(-a) + b = b + (-a) = b + additive inverse of a.
32. __________ ÷ (- 10) = 0
Ans: 0
Let the missing number to be x.
$x \div \left( { - 10} \right) = 0$
$\Rightarrow \dfrac{x}{{ - 10}} = 0$
$\Rightarrow x = 0$
33. (- 157) × (- 19) + 157 =___________.
Ans: 3140
$\left( { - 157} \right){\text{ }} \times {\text{ }}\left( { - 19} \right){\text{ }} + {\text{ }}157{\text{ }} = {\text{ }}157{\text{ }} \times {\text{ }}19{\text{ }} + {\text{ }}157{\text{ }} \times {\text{ }}1$
$={\text{ }}157{\text{ }} \times {\text{ }}\left[ {19{\text{ }} + {\text{ }}1} \right]{\text{ }}$
$={\text{ }}157{\text{ }} \times {\text{ }}20{\text{ }}$
$={\text{ }}3140$
34. [(- 8) + ___] + ___ = ___ + [(-3) + ___] = – 3
Ans: -3, 8, -8, 8
[(-8) + (-3)] + 8 = -8 + [(-3) + 8] = -3
35. On the following number line, (- 4) × 3 is represented by the point_____ .
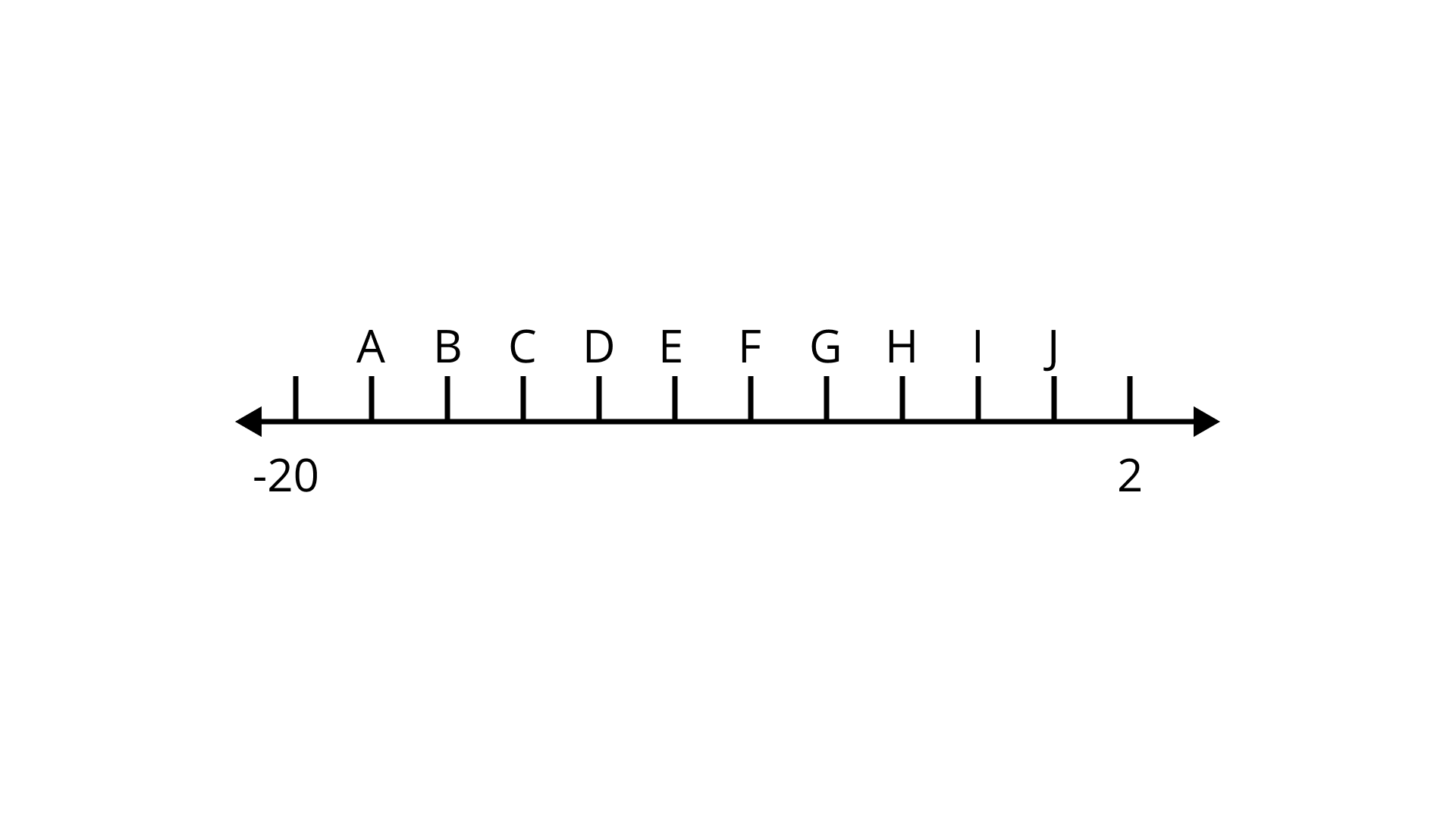
Ans: D
-20-(-4) × 2 = – 12
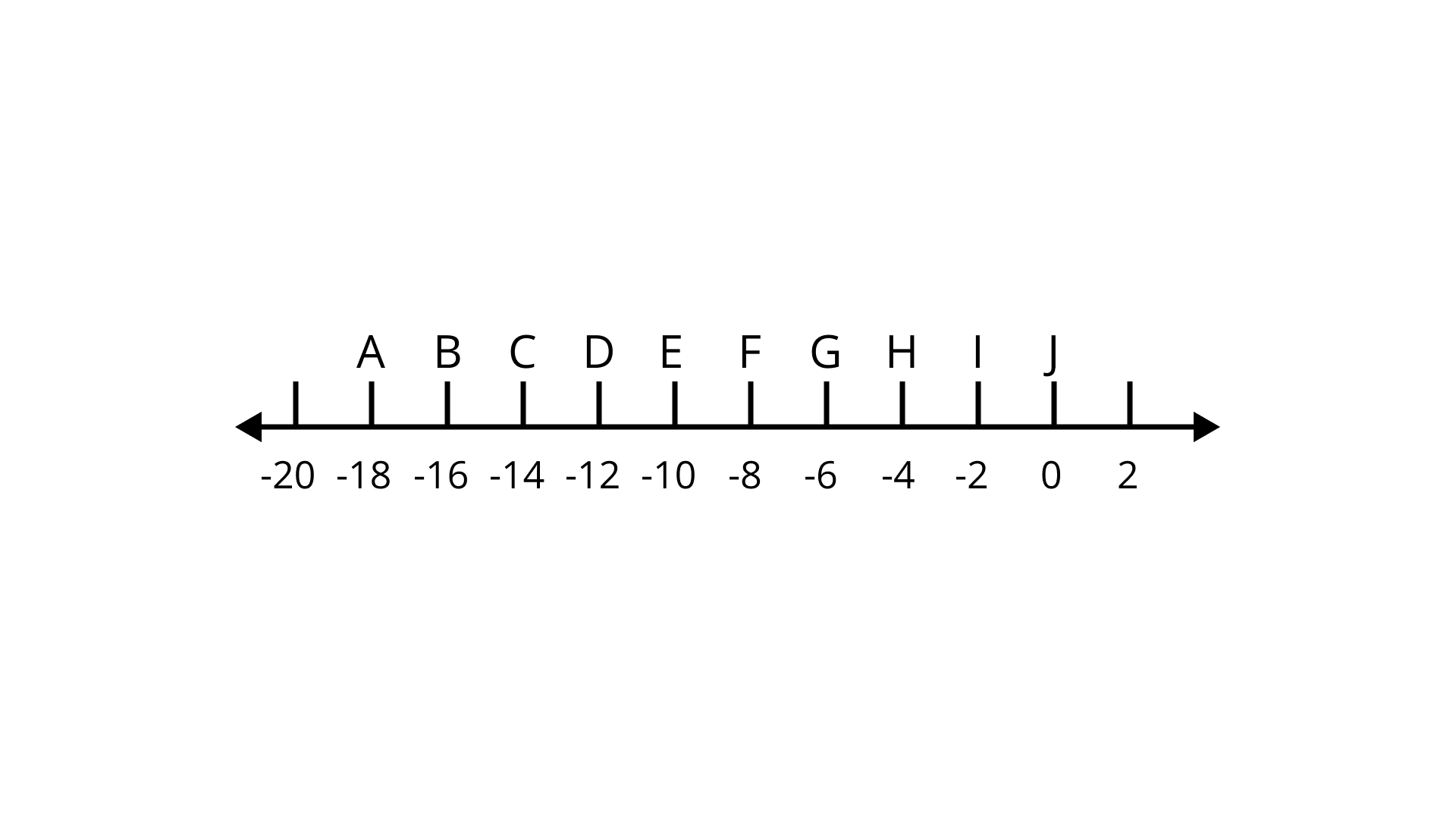
So, D represents -12.
36. If x, y and z are integers, then (x +____) + z =____ + (y +____)
Ans: y, x, z
(x + y) + z = x + (y + z) (Associative property of integers)
37. (-43) + __________ = (-43)
Ans: 0
Let the missing number be x.
(-43) + x = – 43
x = -43 + 43 = 0
38. (- 8) + (- 8) + (- 8) =_______ × (- 8)
Ans: 3
Let the missing number be x.
$\left( { - 8} \right){\text{ }} + {\text{ }}\left( { - 8} \right){\text{ }} + {\text{ }}\left( { - 8} \right){\text{ }} = {\text{ }}x{\text{ }} \times {\text{ }}\left( { - 8} \right)$
$3\left( { - 8} \right) = {\text{ }}x{\text{ }} \times {\text{ }}\left( { - 8} \right){\text{ }}$
$x = {\text{ }}3{\text{ }}$
39. 11 × (- 5) = – (_____ x____) =_____
Ans: 11, 5, -55
11 × (-5) = -(11 × 5) = -55
40. (- 9) × 20 =_______
Ans: -180
Let the missing number to be x.
(-9) × 20 = x
x = -180
41. (- 23) × (42) = (- 42) ×______
Ans: 23
(-23) × (42) = (-42) × (23)
42. While multiplying a positive integer and a negative integer, we multiply them as ___ numbers and put a ___ sign before the product.
Ans: Whole, negative
43. If we multiply___ number of negative integers, then the resulting integer is positive.
Ans: Even
44. If we multiply six negative integers and six positive integers, then the resulting integer is___.
Ans: Positive
When even numbers of negative integers are multiplied, they give positive integers and when positive integers are multiplied, they always give positive integers.
45. If we multiply five positive integers and one negative integer, then the resulting integer is ___.
Ans: Negative
When an odd number of negative integers multiplied, they give a negative integer. Also, when a negative and a positive integer are multiplied, they give a negative integer.
46. ________ is the multiplicative identity for integers.
Ans: 1
e.g. if a is an integer then a × 1 = 1 × a = a.
47. We get the additive inverse of an integer a, when we multiply it by ___.
Ans: (-1)
a × (-1) = -a
48. (- 25) × (- 2) =______.
Ans: 50
Let the missing number to be x.
(-25) × (-2) = x
25 × 2 = x
So, x = 50
49. (- 5) × (- 6) × (- 7) =______.
Ans: -210
Let the missing number to be x.
(-5) × (-6) × (-7) = x
5 × 6 × (-7) = x
30 × (-7) = x
So, x = -210
50. 3 × (- 1) × (- 15) =_______.
Ans: 45
Let the missing number to be x.
3 × (-1) × (-15) = x
x = (-3) × (-15) = 45
51. $\left[12 × (- 7)\right]$ × 5 =_____ × (- 7) × ____
Ans: 12, 5
\[\left[ {12{\text{ }} \times {\text{ }}\left( { - {\text{ }}7} \right)} \right]{\text{ }} \times {\text{ }}5{\text{ }} = {\text{ }}12{\text{ }} \times {\text{ }}\left[ {\left( { - {\text{ }}7} \right){\text{ }} \times {\text{ }}5} \right]\]
52. 23 × (- 99) = ____ × (- 100 + ____) = 23 × ____ + 23 × ____
Ans: 23, 1, -100, 1
23 × (- 99) = 23 × (- 100 + 1) = 23 × (- 100) + 23 × 1
53. ______ × (- 1) = – 35
Ans: 35
Let the missing number to be x.
x × (-1) = – 35
So, x = 35
54. ____ × (- 1) = 47
Ans: -47
Let the missing number to be x.
x × (- 1) = 47
So, x = -47
55. 88 × ____ = – 88
Ans: -1
Let the missing number to be x.
88 × x = – 88
So, x = -1
56. ____ × (- 93) = 93
Ans: -1
Let the missing number to be x.
x × (- 93) = 93
So, x = -1
57. (- 40) × ___ = 80
Ans: -2
Let the missing number to be x.
(- 40) × x = 80
$ \Rightarrow x = \dfrac{{80}}{{ - 40}} = - 2$
58. ____ × (-23) = – 920
Ans: 40
Let a number be multiplied by x.
x × (-23) = -920
\[ \Rightarrow x{\text{ }} = {\text{ }} - 920{\text{ }} \div {\text{ }}\left( { - 23} \right){\text{ }} = {\text{ }}\dfrac{{920}}{{23}}{\text{ }} = {\text{ }}40\]
59. When we divide a negative integer by a positive integer, we divide them as whole numbers and put a ____ sign before quotient.
Ans: Negative
60. When (-16) is divided by ____ the quotient is 4.
Ans: -4
Let -16 be divided by x gives the quotient 4.
\[ \Rightarrow 4{\text{ }} = \dfrac{{ - 16}}{x} \]
\[ \Rightarrow x{\text{ }} = \dfrac{{ - 16}}{4} = - 4\]
61. Division is the inverse operation of ____.
Ans: Multiplication.
62. 65 ÷ (- 13) =_____.
Ans: −5
Let the missing number to be x.
$65 \div \left( { - 13} \right) = x$
$\Rightarrow x = \dfrac{{ - 65}}{{13}} = - 5$
63. (-100) ÷ (-10) =_____.
Ans: 10
Let the missing number to be x.
$\left( { - 100} \right) \div \left( { - 10} \right) = x$
$\Rightarrow x = \dfrac{{100}}{{10}} = 10$
64. (-225) ÷ 5 = _____.
Ans: −45
Let the missing number to be x.
$\left( { - 225} \right) \div 5 = x$
$\Rightarrow x = \dfrac{{ - 225}}{5} = - 45$
65. _____ ÷ (-1) = (- 83)
Ans: 83
Let the missing number to be x.
x ÷ (-1) = – 83
$\Rightarrow x = - 83 \times \left( { - 1} \right) = 83$
66. ____ ÷ (-1) = 75
Ans: −75
Let the missing number to be x.
$x \div \left( { - 1} \right) = 75$
$\Rightarrow x = 75 \times \left( { - 1} \right) = - 75$
67. 51 ÷ ____ = (-51)
Ans: −1
Let the missing number to be x.
$51 \div x = \left( { - 51} \right)$
$\Rightarrow x = \dfrac{{51}}{{ - 51}} = - 1$
68. 113 ÷ ____ = (- 1)
Ans: −113
Let the missing number to be x.
$113 \div x = \left( { - 1} \right)$
$\Rightarrow x = \dfrac{{113}}{{ - 1}} = - 113$
69. -95 ÷ ____ = 95
Ans: −1
Let the missing number to be x.
$- 95 \div x = 95$
$\Rightarrow x = \dfrac{{ - 95}}{{95}} = - 1$
70. (-69) ÷ 69 =_____.
Ans: −1
Let the missing number to be x.
$\left( { - 69} \right) \div 69 = x$
$\Rightarrow x = \dfrac{{ - 69}}{{69}} = - 1$
71. (-28) ÷ (-28) = _____
Ans: 1
Let the missing number to be x.
$\left( { - 28} \right) \div \left( { - 28} \right) = x$
$\Rightarrow x = \dfrac{{ - 28}}{{ - 28}} = 1$
Directions: In questions 72 to 108, state whether the statements are true or false.
72. 5 – (-8) is the same as 5 + 8.
Ans: True
5 – (-8) = 5 + 8
73. (-9) + (-11) is greater than (-9) – (- 11).
Ans: False
(-9) + (-11) = – 9 – 11 = -20
And (-9) – (-11) = -9 + 11 = 2
Since, -20 < 2
⇒ -9 + (-11) < (-9) – (-11)
74. Sum of two negative integers always gives a number smaller than both the integers.
Ans: True
75. Difference of two negative integers cannot be a positive integer.
Ans: False
As -3 – (-5) = -3 + 5 = 2
76. We can write a pair of integers, whose sum is not an integer.
Ans: False
Since, the sum of two integers is always an integer.
77. Integers are closed under subtraction.
Ans: True
The subtraction of any two integers is always an integer.
So, integers are closed under subtraction.
78. (- 23) + 47 is the same as 47 + (- 23).
Ans: True
(-23) + 47 = 24
And 47 + (-23) = 47 – 23 = 24
79. When we change the order of integers their sum remains the same.
Ans: True
80. When we change the order of integers, their difference remains the same.
Ans: False
As 2 – 3 – 5 = 2 – 8 = -6
but 3 – 2 – 5 = 3 – 7 = -4
81. Going 500 m towards East first and then 200 m back, is same as going 200 m towards West first and then going 500 m back.
Ans: True
In the first case, he is at a distance of (500 – 200) m = 300 m towards east.
In the second case, he is at a distance of (200 – 500) m = -300 m towards west i.e., 300 m towards east.
82. (-5) × (33) = 5 × (- 33)
Ans: True
(-5) × (33) = – 165 = 5 × (-33)
83. (-19) × (-11) = 19 × 11
Ans: True
(-19) × (-11) = 19 × 11 = 209
84. (-20) × (5 – 3) = (-20) × (-2)
Ans: False
(-20) × (5 – 3) = (-20) × 2 = (-40)
but (-20) × (-2) = 20 × 2 = 40
85. 4 × (-5) = (-10) × (-2)
Ans: False
4 × (-5) = – 20
But (-10) × (-2) = 10 × 2 = 20
86. (-1) × (-2) × (-3) = 1 × 2 × 3
Ans: False
(-1) × (-2) × (-3) = 1 × 2 × (-3) = 2 × (-3) = (-6)
But 1 × 2 × 3 = 6
87. (-3) × 3 = (-12) – (-3)
Ans: True
Since, (-3) × 3 = (- 9)
And (-12) – (-3) = (-12) + 3 = (-9)
88. Product of two negative integers is a negative integer.
Ans: False
A product of two negative integers is always a positive integer.
89. Product of three negative integers is a negative integer.
Ans: True
Since, the product of odd numbers of negative integers is always a negative integer.
90. Product of a negative integer and a positive integer is a positive integer.
Ans: False
A product of a negative integer and a positive integer is a negative integer.
91. When we multiply two integers their product is always greater than both the integers.
Ans: False
When two integers are multiplied then their product may or may not be greater than both the integers.
92. Integers are closed under multiplication.
Ans: True
Since, multiplication of two integers is always an integer.
Integers are closed under multiplication.
93. (-237) × 0 is the same as 0 × (-39).
Ans: True
(-237) × 0 = 0
And 0 × (-39) = 0
94. Multiplication is not commutative for integers.
Ans: False
Multiplication is commutative for integers. For example, 2 x 3 = 6 also 3 x 2 = 6.
95. (-1) is not a multiplicative identity of integers.
Ans: True
1 is multiplicative identity for integers.
96. 99 × 101 can be written as (100 – 1) × (100 + 1).
Ans: True
99 = 100 – 1 and 101 = 100 + 1
So, 99 × 101 = (100 – 1) × (100 + 1)
97. If a, b and c are integers and b ≠ 0, then a × (b – c) = a × b – a × c
Ans: True
Use distributive property of multiplication over subtraction,
a × (b – c) = (a × b) – (a × c)
98. (a + b) × c = a × c + a × b
Ans: False
Use distributive property of multiplication over addition,
a × (b + c) = a × b + a × c
99. a × b = b × a
Ans: True
If a = 2 and b = 5, a x b = 2 x 5 = 10
And 5 x 2 = 10
100. a ÷ b = b ÷ a
Ans: False
As division is not commutative for integers,
So, a ÷ b ≠ b ÷ a
101. a – b = b – a
Ans: False
As subtraction is not commutative for integers.
So, a – b ≠ b – a
102. a ÷ (- b) = – (a ÷ b)
Ans: True
$a \div \left( { - b} \right) = -\dfrac{{ a}}{b}$
$- \left( {a \div b} \right) = - \dfrac{a}{b}$
103. a ÷ (-1) = – a
Ans: True
\[a \div \left( { - 1} \right) = \dfrac{a}{{ - 1}} = - a\]
104. Multiplication fact (-8) × (-10) = 80 is the same as division fact 80 ÷ (-8) = (-10).
Ans: True
(-8) × (-10) = 8 × 10 = 80
And \[80 \div \left( { - 8} \right) = \dfrac{{ - 80}}{8} = - 10\]
105. Integers are closed under division.
Ans: False
Consider two integers 3 and 4.
3 ÷ 4 = $\dfrac{3}{4}$ which is not integer.
So, integers are not closed under division.
106. $\left[ {\left( { - 32} \right) \div 8} \right] \div 2 = - 32 \div \left[ {8 \div 2} \right]$
Ans: False
$\left[ {\left( { - 32} \right) \div 8} \right] \div 2 = \left[ { - \dfrac{{32}}{8}} \right] \div 2 = - 4 \div 2 = \dfrac{{ - 4}}{2} = - 2$
But $ - 32 \div \left[ {8 \div 2} \right] = - 32 \div 4 = \dfrac{{ - 32}}{4} = - 8$
107. The sum of an integer and its additive inverse is zero (0).
Ans: True
Let any integer be a.
Its additive inverse is -a.
a + (-a) = a – a = 0
108. The successor of 0 × (-25) is 1 × (-25).
Ans: False
0 × (-25) = 0 and 1 × (-25) = -25
But the successor of 0 is 1.
109. Observe the following patterns and fill in the blanks to make the statements true:
(a) – 5 × 4 = – 20
-5 × 3 = -15 = -20 – (-5)
-5 × 2 =_____ = -15 – (-5)
-5 × 1 =_____ = ______
-5 × 0 = 0 =_______
-5 × -1 = 5 = _____
– 5 × – 2 =__ =______
Ans: -10, -5, -10 – (-5), -5 – (-5), 0 – (-5), 10, 5 – (-5)
-5 × 2 = -10 = -15 – (-5)
-5 × 1 = -5 = -10 – (-5)
-5 × 0 = 0 = -5 – (-5)
-5 × -1 = 5 = 0 – (-5)
-5 × – 2 =10 = 5 – (-5)
(b) 7 × 4 = 28
7 × 3 =______ = 28 – 7
7 × 2 =______ =____ – 7
7 × 1 = 7 =____ -7
7 × 0 =______ =____ -______
7 × – 1 = -7 =__ -______
7 × – 2 =___ =______ -_____
7 × – 3_____ =____ -______
Ans: 21, 14, 21, 14, 0, 7, 7, 0, 7, -14, -7, 7, -21, -14, 7
7 × 3 = 21 = 28 – 7
7 × 2 = 14 = 21 – 7
7 × 1 = 7 = 14 – 7
7 × 0 = 0 = 7 – 7
7 × (- 1) = -7 = 0 – 7
7 × (- 2) = -14 = -7 – 7
7 × (- 3) = -21 = -14 – 7
110. Science Application An atom consists of charged particles called electrons and protons. Each proton has a charge of +1 and each electron has a charge of -1. Remember number of electrons is equal to number of protons, while answering these questions:
(a) What is the charge on an atom?
Ans: Atoms have two charged particles proton and electron. Protons have +1 charge and electrons have -1 charge.
Then, total charge = +1 – 1 = 0
(b) What will be the charge on an atom, if it loses an electron?
Ans: If an atom loses an electron, then the charge on the atom will be of proton so charge of atom will be +1.
(c) What will be the charge on an atom, if it gains an electron?
Ans: As calculated in part (a) total charge on atoms is 0. Then the charge on an atom if it gains an electron is -1 i.e. charge of electron gained.
111. An atom changes to a charged particle called an ion, if it loses or gains electrons. The charge on an ion is the charge on electrons plus charge on protons. Now, write the missing information in the table given below:
Name of Ion | Proton Charge | Electron Charge | Ion Charge |
Hydroxide ion | +9 | - | -1 |
Sodium ion | +11 | - | +1 |
Aluminum ion | +13 | -10 | - |
Oxide ion | +8 | -10 | - |
Ans: Hydroxide ion charge = Proton charge + Electron charge
⇒ -1 = +9 + Electron charge
⇒ Electron charge = -1 – 9 = – 10
Sodium ion charge = Proton charge + Electron charge
⇒ +1 = +11 + Electron charge
⇒ Electron charge = +1 – 11 = -10
Aluminum ion charge = Proton charge + Electron charge
⇒ +13 + (-10) = +13 – 10 = +3
Oxide ion charge = Proton charge + Electron charge
⇒ +8 + (-10) = +8 – 10 = -2
Name of Ion | Proton Charge | Electron Charge | Ion Charge |
Hydroxide ion | +9 | -10 | -1 |
Sodium ion | +11 | -10 | +1 |
Aluminum ion | +13 | -10 | +3 |
Oxide ion | +8 | -10 | -2 |
112. Social Studies Application remembering that 1AD came immediately after 1 BC, while solving following problems take 1BC as -1 and 1AD as + 1.
(a) The Greco-Roman era, when Greece and Rome ruled Egypt, started in the year 330 BC and ended in the year 395 AD. How long did this era last?
Ans: Given 1 BC as -1 and 1 AD as +1.
Starting year = 330 BC = (-330) AD
Ending year = 395 AD
The era lasted for = 395 – (-330) = 395 + 330 = 725 years
(b) Shankaracharya was born in the year 1114 AD and died in the year 1185 AD. What was his age when he died?
Ans: Born year = 1114 AD
Death year = 1185 AD
So, total age = 1185 – 1114 = 71 years
(c) Turks ruled Egypt in the year 1517 AD and Queen Nefertis ruled. Egypt about 2900 years before the Turks ruled. In what year did she rule?
Ans: Turks ruled Egypt in 1517 AD.
Queen Nefertis ruled Egypt in (1517-2900) AD= -1383 AD or 1383 BC.
(d) Greek Mathematician Archimedes lived between 287 BC and 212 BC and Aristotle lived between 380 BC and 322 BC. Who lived during an earlier period?
Ans: Archimedes lived between 287 BC and 212 BC.
Aristotle lived between 380 BC and 322 BC.
So, Aristotle lived during an earlier period.
113. The table shows the lowest recorded temperatures for each continent. Write the continents in order from the lowest recorded temperature to the highest recorded temperature.
The Lowest Recorded Temperatures | |
Continent | Temperature (in Fahrenheit) |
Africa | -11° |
Antarctica | -129° |
Asia | -90° |
Australia | -9° |
Europe | -67° |
North America | -81° |
South America | -27° |
Ans: Since, -129° < -90° < -81° < -67° < -27° < -11° < -9°
Therefore, the order of the continents from the lowest to the highest recorded temperature is Antarctica, Asia, North America, Europe, South America, Africa, Australia.
114. Write a pair of integers whose product is -12 and there lies seven integers between them (excluding the given integers).
Ans: Let the integers be -2 and 6 such that (-2) × 6 = -12
So, a pair of integers is (-2, 6).
And there are seven integers, i.e., -1, 0, 1, 2, 3, 4, 5 which lie between -2 and 6.
115. From given integers in Column I, match an integer of Column II, so that their product lies between -19 and -6.
Column I | Column II |
-5 | 1 |
6 | -1 |
-7 | 3 |
8 | -2 |
Ans:
-5 → 3; 6 → -2; -7 → 1; 8 → -1;
-5 × 3 = -15, also -19 < -15 < -6
6 × (-2) = -12, also -19 < -12 < -6
-7 × 1 = -7, also -19 < -7 < -6
8 × (-1) = -8, also -19 < -8 < -6
116. Write a pair of integers, whose product is -36 and whose difference is 15.
Ans: Let the integers be 12 and -3 such that 12 × (-3) = -36
and their difference = 12 – (-3) = 12 + 3 = 15
Therefore, a pair of integers is (-3, 12).
117. Match the following:
Column I | Column II | ||
(a) | a × 1 | (i) | Additive inverse of a |
(b) | 1 | (ii) | Additive identity |
(c) | (-a) ÷ (-b) | (iii) | Multiplicative identity |
(d) | a × (-1) | (iv) | a ÷ (-b) |
(e) | a × 0 | (v) | a ÷ b |
(f) | (-a) ÷ b | (vi) | a |
(g) | 0 | (vii) | -a |
(h) | a ÷ (-a) | (viii) | 0 |
(i) | -a | (ix) | -1 |
Ans:
(a) → (vi)
a x 1 = a
(b) → (iii)
1 is multiplicative identity.
(c) → (v)
-a ÷ (-b) = a ÷ b (both signs are cancelled with each other)
(d) → (vii)
a x (-1) = -a
(e) → (viii)
a x 0 = 0 (any value, when multiplies with 0 becomes zero)
(f) → (iv)
(-a) ÷ b = a ÷ (-b)
(g) → (ii)
0 is an additive identity.
(h) → (ix)
a ÷ (-a) = -a
(i) → (i)
-a is the additive inverse of a.
118. You have ₹ 500 in your saving account at the beginning of the month. The record below, shows all of your transactions during the month. How much money is in your account after these transactions?
Cheque No. | Date | Transaction Description | Payment | Deposit |
384102 275146 | 4/9 12/9 | Jal Board Deposit | ₹ 120 | ₹ 200 |
384103 801351 | 22/9 29/9 | LIC India Deposit | ₹ 240 | ₹ 150 |
Ans: Money left in the account after given transactions = ₹ (500 + 200 + 150 – 120 – 240)
= ₹ (850 – 360) = ₹ 490
119. (a) Write a positive integer and a negative integer whose sum is a negative integer.
Ans: 2 + (-3) = -1
(b) Write a positive integer and a negative integer whose sum is a positive integer.
Ans: 3 + (-2) = 1
(c) Write a positive integer and a negative integer whose difference is a negative integer.
Ans: -1 – (4) = -5
(d) Write a positive integer and a negative integer whose difference is a positive integer.
Ans: 4 – (-1) = 5
(e) Write two integers which are smaller than – 5 but their difference is – 5.
Ans: -7 < -5, -12 < -5 and -12 – (-7) = -5
(f) Write two integers which are greater than -10 but their sum is smaller than -10.
Ans: -5 > -10, -6 >-10 and-5 +(-6) = -11 < -10
(g) Write two integers which are greater than – 4 but their difference is smaller than – 4.
Ans: 2 > -4, -3 > -4 and -3 – 2 = -5 < -4
(h) Write two integers which are smaller than – 6 but their difference is greater than – 6.
Ans: -7 < -6, -8 < -6 and -7 – (-8) = -7 + 8 = 1 > -6
(i) Write two negative integers whose difference is 7.
Ans: -3 – (-10) = -3 + 10 = 7
(j) Write two integers such that one is smaller than -11, and other is greater than -11 but their difference is -11.
Ans: -18 < -11; -7 >-11 and -18 – (-7) = -18 + 7 = -11
(k) Write two integers whose product is smaller than both the integers.
Ans: (-1) × (2) = -2. Also, -2 < -1 and -2 < 2
(l) Write two integers whose product is greater than both the integers.
Ans: 4 × 5 = 20. Also, 4 < 20 and 5 < 20
120. What’s the error? Ramu evaluated the expression – 7 – (-3) and came up with the answer – 10. What did Ramu do wrong?
Ans: Ramu did -7 – 3, so he got -10.
But it should be done like -7 – (-3) = -7 + 3 = -4. Ramu has done addition in place of subtraction.
121. What’s the error? Reeta evaluated -4 + d for d = – 6 and gave an answer of 2. What might Reeta have done wrong?
Ans: Since -4 + (-6) = -10,
But -4 – (-6) = -4 + 6 = 2
Hence, Reeta has done subtraction in place of addition.
122. The table given below, shows the elevations relative to sea level of four locations. Taking sea level as zero (0), answer the following questions.
Location | Elevation(in m) |
A | -180 |
B | 1600 |
C | -55 |
D | 3200 |
(a) Which location is closest to sea level?
Ans: C is closest to sea level.
(b) Which location is farthest from sea level?
Ans: D is farthest from sea level.
(c) Arrange the locations from the least to the greatest elevation.
Ans: Since, -180 < -55 < 1600 < 3200.
Therefore, the location from the least to the greatest elevation is A < C < B < D.
123. You are at an elevation 380 m above sea level as you start a motor ride. During the ride, your elevation changes by the following meters 540 m, -268 m, 116 m, -152 m, 490 m, -844 m, 94 m. What is your elevation relative to the sea level at the end of the ride?
Ans: Elevation relative to the sea level at the end of the ride = [380 + 540 – 268 + 116 -152 + 490 – 844 + 94]m
= [380 + 540 + 116 + 490 + 94 – 268 – 152 – 844] m
= [1620 – 1264] m = 356 m
124. Evaluate the following, using distributive property.
(i) -39 × 99
Ans: -3861
$- 39{\text{ }} \times {\text{ }}99{\text{ }} = {\text{ }} - 39{\text{ }} \times {\text{ }}\left( {100{\text{ }} - 1} \right)$
$={\text{ }} - 39{\text{ }} \times {\text{ }}100{\text{ }} + {\text{ }}\left( { - 39} \right){\text{ }} \times {\text{ }}\left( { - 1} \right)$
$={\text{ }} - 3900{\text{ }} + {\text{ }}39{\text{ }}$
$={\text{ }} - 3861$
(ii) (-85) × 43 +43 × (-15)
Ans: $\left( { - 85} \right){\text{ }} \times {\text{ }}43{\text{ }} + {\text{ }}43{\text{ }} \times {\text{ }}\left( { - 15} \right) = {\text{ }}43{\text{ }} \times {\text{ }}\left( { - 85} \right){\text{ }} + {\text{ }}43{\text{ }} \times {\text{ }}\left( { - 15} \right)$
$={\text{ }}43{\text{ }} \times {\text{ }}\left[ { - 85{\text{ }}-{\text{ }}15} \right]$
$={\text{ }}43{\text{ }} \times {\text{ }}\left[ { - 100} \right]{\text{ }}$
$={\text{ }} - 4300$
(iii) 53 × (-9) – (-109) × 53
Ans: $53{\text{ }} \times {\text{ }}\left( { - 9} \right){\text{ }}-{\text{ }}\left( { - 109} \right){\text{ }} \times {\text{ }}53 = {\text{ }}53{\text{ }} \times {\text{ }}\left( { - 9} \right){\text{ }}-{\text{ }}53{\text{ }} \times {\text{ }}\left( { - 109} \right)$
$={\text{ }}53{\text{ }} \times {\text{ }}\left[ {\left( { - 9} \right){\text{ }}-{\text{ }}\left( { - 109} \right)} \right]$
$={\text{ }}53{\text{ }} \times {\text{ }}\left[ { - 9{\text{ }} + {\text{ }}109} \right]{\text{ }}$
$={\text{ }}53{\text{ }} \times {\text{ }}100{\text{ }}$
$={\text{ }}5300$
(iv) 68 × (-17) + (-68) × 3
Ans: $68{\text{ }} \times {\text{ }}\left( { - 17} \right){\text{ }} + {\text{ }}\left( { - 68} \right){\text{ }} \times {\text{ }}3{\text{ }} = {\text{ }}68{\text{ }} \times {\text{ }}\left( { - 17} \right){\text{ }} + {\text{ }}68{\text{ }} \times {\text{ }}\left( { - 3} \right)$
$={\text{ }}68{\text{ }} \times {\text{ }}\left[ {\left( { - 17} \right){\text{ }} + {\text{ }}\left( { - 3} \right)} \right]$
$={\text{ }}68{\text{ }} \times {\text{ }}\left( { - 20} \right){\text{ }}$
$={\text{ }} - 1360$
125. If ‘*’ is an operation for integers a and b. We have a * b = a × b + (a × a + b × b), then find
(i) (-3) * (-5)
Ans: We have,
a * b = a × b +(a × a + b × b)
Now, put a = (-3) and b = (-5)
(-3)* (-5) = (- 3) × (- 5)+ $\left[(- 3) × (- 3)+ (- 5) × (- 5)\right]$
= 15 + (9 + 25) = 15 + 34 = 49
(ii) (-6) * 2
Ans: Put a = – 6 and b = 2
(-6) * 2 = (-6) × 2 + $\left[(-6) × (-6) + 2 × 2\right]$
= -6 × 2 + (36 + 4) = -12 + 40 = 28
126. If Δ is an operation such that for integers a and b we have a Δ b = a × b – 2 × a × b + b × b (-a) × b + b × b then find
(i) 4 Δ (- 3)
(ii) (- 7) Δ (- 1)
Also show that 4 Δ (- 3) ≠ (- 3) Δ 4 and (-7) Δ (-1) ≠ (-1) Δ (- 7)
Ans: Given, a Δ b = a × b – 2 × a × b + b × b (-a) × b + b × b
(i) 4 Δ (-3) = 4 × (-3) – 2 × 4 × (-3) + (-3) × (-3)(-4) × (-3) + (-3) × (-3)
= -12 + 24 + 108 + 9 = -12 + 141 = 129
(ii) (-7) Δ (-1) = (-7) × (-1) – 2 × (-7) × (-1) + (-1) × (-1) (7) × (-1) + (-1) × (-1)
= 7 – 14 – 7 + 1 = 8 – 21 = -13
Now, (-3) Δ 4 = (-3) × 4 – 2 × (-3) × (4) + 4 × 4(3) × 4 + 4 × 4
= -12 + 24 + 192 + 16 = -12 + 232 = 220
But 4 Δ (-3) = 129
Therefore, 4 Δ (-3) ≠ (-3) Δ 4.
And, (-1) Δ (-7) = (-1) × (-7) – 2 × (-1) × (-7) + (-7) × (-7)(1) × (-7) + (-7) × (-7)
= 7 – 14 – 343 + 49 = 56 – 357 = -301
But (-7) Δ (-1) = -13
Therefore, (-7) Δ (-1) ≠ (-1) Δ (-7).
127. Below u, v, w and x represent different integers, where u = (-4) and x ≠ 1. By using following equations, find each of the values
u × v = u
x × w =w
u + x = w
Explain your reason, using the properties of integers
(a) v
Ans: As u × v = u and u = -4
∴ -4 × v = -4
⇒ v = l (Multiplicative identity)
(b) w
Ans: As x × w = w. Given that x ≠ 1
∴ x × w = w is only possible when w = 0
(c) x
Ans: As u + x = w,
Put u = – 4 and w = 0
∴ -4 + x = 0
⇒ x = 4 (Transposing -4 to R.H.S.)
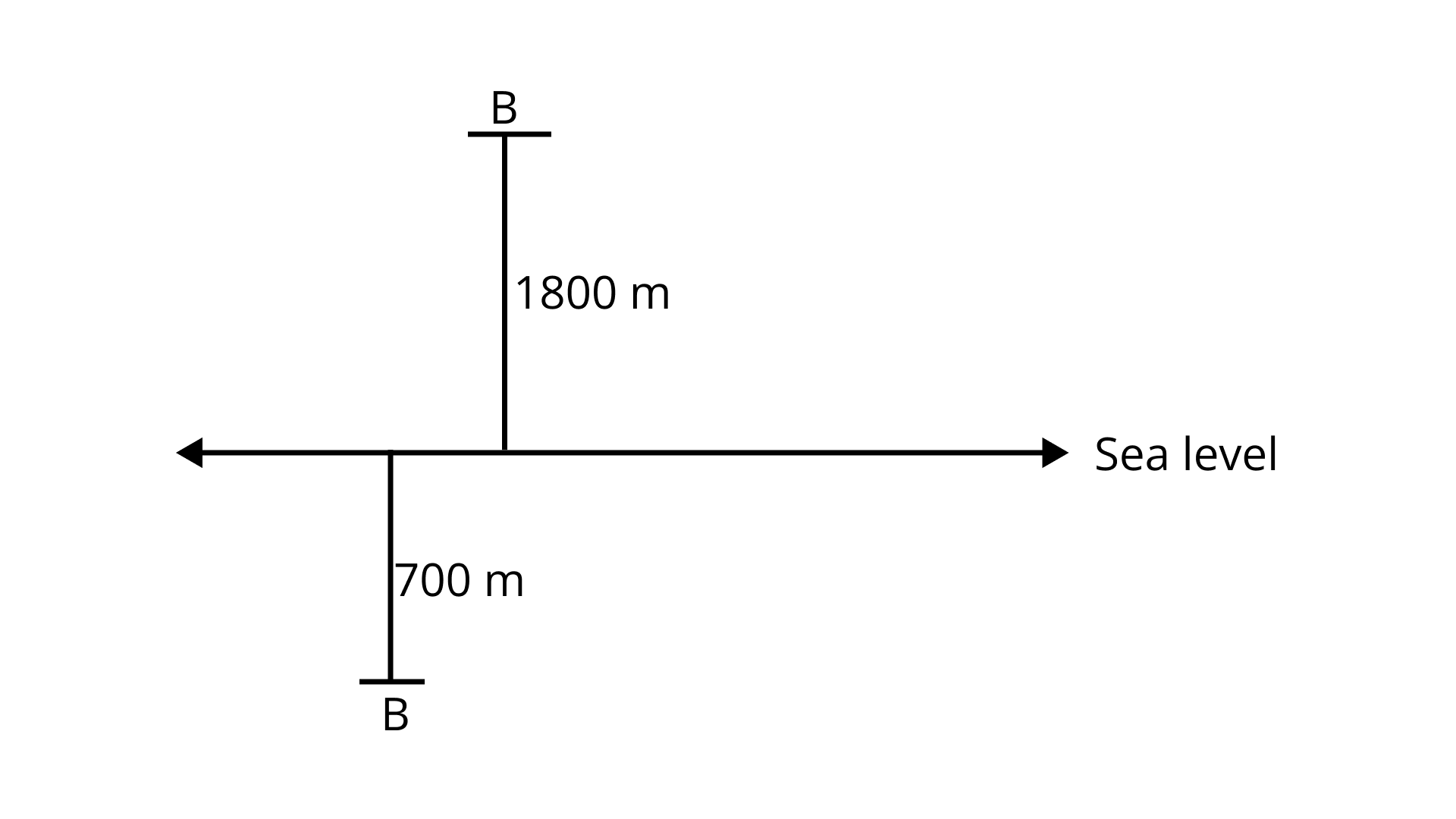
128. Height of a place A is 1800 m above sea level. Another place B is 700 m below sea level. What is the difference between the levels of these two places?
Ans: Difference between the levels of places A and B is $\left[1800 – (-700)right]$ m = (1800 + 700)m = 2500 m
129. The given table shows the freezing points in °F of different gases at sea level. Convert each of these into °C to the nearest integral value using the relation and complete the table,
\[C{\text{ }} = {\text{ }}\dfrac{5}{9}\left( {F - 32} \right)\]
Gas | Freezing Point at Sea Level (°F) | Freezing Point at Sea Level (°C) |
Hydrogen | -435 | |
Krypton | -251 | |
Oxygen | -369 | |
Helium | -458 | |
Argon | -309 |
Ans:
Given relation is \[C{\text{ }} = {\text{ }}\dfrac{5}{9}\left( {F - 32} \right)\].
For hydrogen,
$C{\text{ }} = {\text{ }}\dfrac{5}{9}\left( { - 435 - 32} \right) = \dfrac{5}{9}\left( { - 467} \right)$
$=\dfrac{{ - 2335}}{9} = - 259.44{\text{ }}^\circ {\text{C}}$
So, the nearest integer value is -259°C.
For Krypton,
$C{\text{ }} = {\text{ }}\dfrac{5}{9}\left( { - 251 - 32} \right) = \dfrac{5}{9}\left( { - 283} \right)$
$=\dfrac{{ - 1415}}{9} = - 157.22{\text{ }}^\circ {\text{C}}$
So, the nearest integer value is -157°C.
For Oxygen,
$C{\text{ }} = {\text{ }}\dfrac{5}{9}\left( { - 369 - 32} \right) = \dfrac{5}{9}\left( { - 401} \right)$
$=\dfrac{{ - 2005}}{9} = - 222.77{\text{ }}^\circ {\text{C}}$
So, the nearest integer value is -222°C.
For Helium,
$C{\text{ }} = {\text{ }}\dfrac{5}{9}\left( { - 458 - 32} \right) = \dfrac{5}{9}\left( { - 490} \right)$
$=\dfrac{{ - 2450}}{9} = - 272.22{\text{ }}^\circ {\text{C}}$
So, the nearest integer value is -272°C.
For hydrogen,
$C{\text{ }} = {\text{ }}\dfrac{5}{9}\left( { - 309 - 32} \right) = \dfrac{5}{9}\left( { - 341} \right)$
$=\dfrac{{ - 1705}}{9} = - 189.44{\text{ }}^\circ {\text{C}}$
So, the nearest integer value is -189°C.
130. Sana and Fatima participated in an apple race. The race was conducted in 6 parts. In the first part, Sana won by 10 seconds. In the second part, she lost by 1 min, then won by 20 seconds in the third part and lost by 25 seconds in the fourth part, she lost by 37 seconds in the fifth part and won by 12 seconds in the last part. Who won the race finally?
Ans: Taking winning by time be a positive integer and losing by time be a negative integer.
Therefore, Sana’s total time (winning or losing the race)
= (10 – 60 + 20 – 25 – 37 + 12) seconds
= (42 – 122) seconds = -80 seconds
Hence, Sana lost the race by 80 seconds or 1 minute 20 seconds i.e., Fatima won the race finally.
131. A green grocer had a profit of ₹ 47 on Monday, a loss of ₹ 12 on Tuesday and loss of ₹ 8 on Wednesday. Find his net profit or loss in 3 days.
Ans: Taking profit as a positive integer and loss as negative integer, we have grocer’s net profit or loss in 3 days = ₹ (47 – 12 – 8) = ₹ 27
Therefore, the grocer has a profit of ₹ 27.
132. In a test, +3 marks are given for every correct answer and -1 mark are given for every incorrect answer. Sona attempted all the s and scored +20 marks, though she got 10 correct answers.
(i) How many incorrect answers has she attempted?
Ans: Total marks scored by Sona = 20
Total correct answers = 10
∴ Marks for correct answers = 10 × 3 = 30
but she got 20 marks.
∴ Marks for incorrect answers = 20 – 30 = – 10
-1 mark is given for every incorrect answer.
Therefore, total incorrect answers = $\dfrac{{ - 10}}{{ - 1}} = 10$
(ii) How many questions were given in the test?
Ans: Total correct answers = 10
Total incorrect answers = 10 (From (i) part)
Therefore, total questions given in the test = 10 + 10 = 20
133. In a true-false test containing 50 s, a student is to be awarded 2 marks for every correct answer and -2 for every incorrect answer and 0 for not supplying any answer. If Yash scored 94 marks in a test, what are the possibilities of his marking correct or wrong answer?
Ans: Yash secured = 94 marks So, minimum correct answers = 94 ÷ 2 = 47
Now, there can be two possibilities :
(1) He attempted 47 correct answers and 3 un-attempted.
(2) He attempted 48 correct and 1 un-attempted and 1 wrong answer.
134. A multistory building has 25 floors above the ground level each of height 5 m. It also has 3 floors in the basement, each of height 5m. A lift in a building moves at a rate of 1 m/s. If a man starts from 50m above the ground, how long will it take him to reach the 2nd floor of the basement?
Ans: Height of each floor = 5 m
∴ Height below the basement to be
covered = 2 × 5m = 10m
If a man starts from 50 m above ground
level and reach the 2nd floor of the basement.
∴ His total distance to be covered = (50 + 10) m = 60 m
Rate of moving of a lift = 1 m/s
∴ A man reach at 2nd floor of basement in 1 × 60 = 60 seconds or 1 minute.
135. Taking today as zero on the number line, if the day before yesterday is 17 January, what is the date 3 days after tomorrow?
Ans:
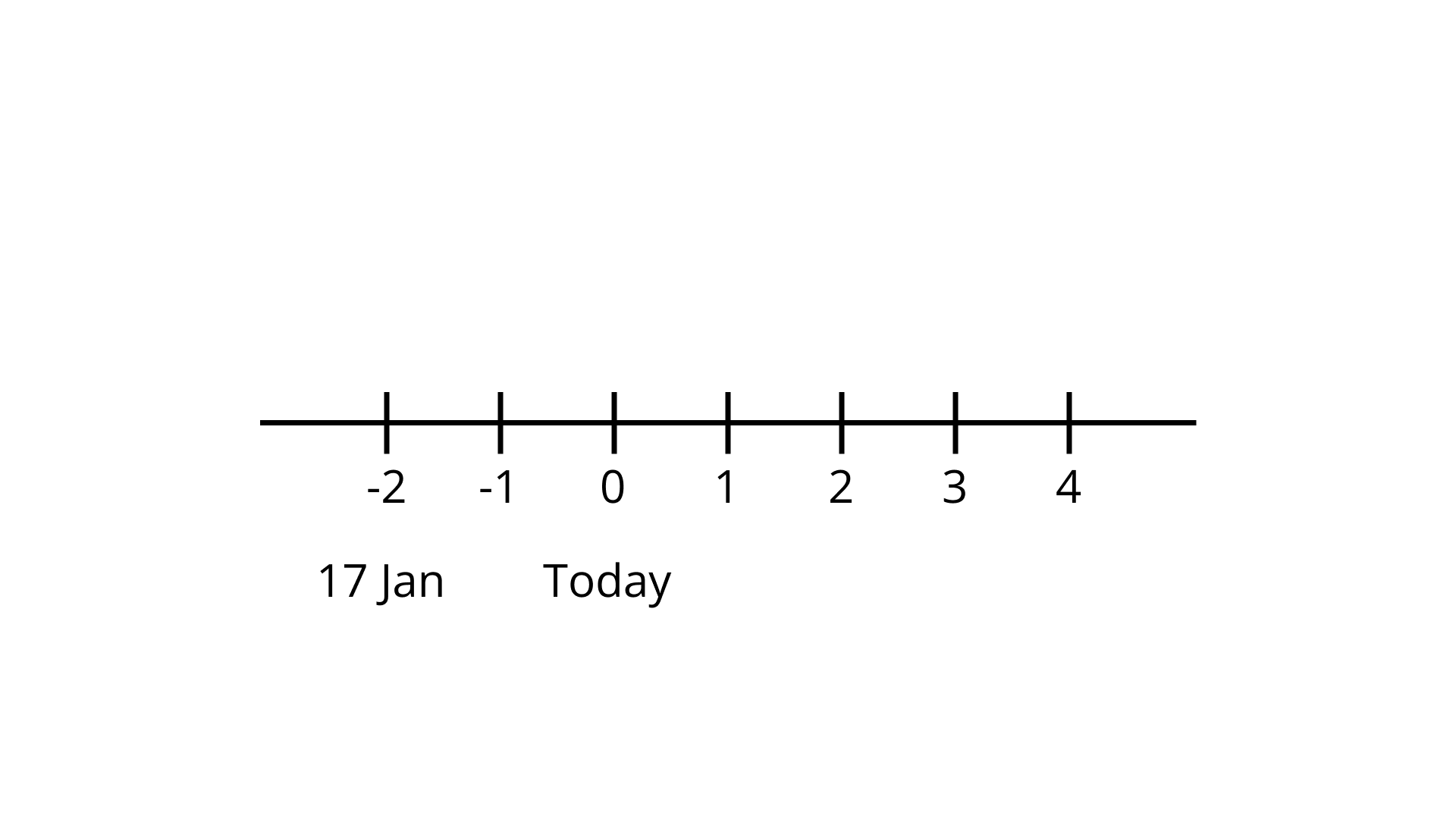
The day before yesterday was 17 January.
So, today is 19 January.
The date 3 days after tomorrow will be 20 January + 3 days = 23 January
136. The highest point measured above sea level is the summit of Mt. Everest, which is 8,848 m above sea level and the lowest point is challenger deep at the bottom of Mariana Trench which is 10,911 m below sea level. What is the vertical distance between these two points?
Ans: The highest point (above sea level) = 8,848 m
The lowest point (below sea level) = 10,911 m
Therefore, total vertical distance between two points = [8,848 – (-10,911)] m
= [8,848 + 10,911] m = 19,759 m
The NCERT Exemplar for Class 7 Math Solutions Chapter 1 Integers is available on Vedantu in PDF format for free download. This PDF contains all the NCERT Exemplar Class 7 Math Chapter 1 Integers questions and their answers to assist students in their revisions and exam preparations. Since Integers is one of the most important concepts of math, the NCERT Exemplar for Class 7 Math Solutions Chapter 1 Integer PDF will surely give you an advantage in the exam. It will help you get better at solving Integer questions and enable you to score the highest marks in your class. Most of the questions in your final exams are quite similar to the ones in the NCERT Exemplar for Class 7 Math Solutions Chapter 1 Integers PDF. That is why you should go through the entire PDF before you appear for your Class 7 Math exam.
What Do You Learn in the Class 7 Math Chapter 1- Integers?
Here is the syllabus of what you will learn in the Class 7 Math Chapter 1 Integers:
Introduction to Integers
Natural Numbers
Whole Numbers
Properties of Addition and Subtraction of Integers
Closure under Addition and subtraction
Commutativity Property for addition
Associativity Property for addition
Additive Identity & Additive Inverse
Additive Identity
Additive inverse
Properties of Multiplication of Integers
Closure under Multiplication
Commutative Property of Multiplication
Multiplication by Zero
Multiplicative Identity
Associative property of Multiplication
Distributive Property of Integers
Division of Integers
Dividing a negative integer by a positive integer
Dividing a positive integer by a negative integer
Dividing a negative integer by a negative integer
The Number Line
Representing integers on a number line
Addition and subtraction of integers using a number line
Addition and Subtraction of Integers
The absolute value of integers
Addition of two positive integers
Addition of two negative integers
Addition of a positive and negative integer
Introduction to Zero
Addition of zero to an integer
Subtraction of zero from an integer, or vice versa
Multiplying an integer with zero
Division of zero by an integer
Properties of Division of Integers
Commutativity
Closure
Multiplication of Integers
Product of two positive integers
Product of two negative integers
Product of one positive and one negative integer
FAQs on NCERT Exemplar for Class 7 Maths Solutions Chapter 1 Integers
1. How to download the NCERT Exemplar for Class 7 Maths Solutions Chapter 1 Integers?
Downloading the NCERT Exemplar for Class 7 Maths Solutions Chapter 1 Integers is not that difficult. All you have to do is visit Vedantu’s website, sign up, look for the NCERT Exemplar for Class 7 Maths Solutions Chapter 1 Integers, and download its PDF file. Apart from this PDF, you will find an unlimited stock of study materials on our website. You can download all these files without spending a single penny. Vedantu does not charge any registration fee and provides all the study resources for free.
2. Is the NCERT Exemplar for Class 7 Maths Solutions Chapter 1 Integers useful?
Yes, the NCERT Exemplar for Class 7 Maths Solutions Chapter 1 Integers is quite helpful for the students. It contains solutions to the NCERT exemplar questions that will help them in their exam preparations. It will help you revise Chapter 1 Integers, which is an important part of the syllabus. An integer is a concept that will come in handy in the subsequent classes. That is why you should go through the NCERT Exemplar for Class 7 Maths Solutions Chapter 1 Integer to understand every aspect of the chapter.
3. Is the NCERT Exemplar for Class 7 Maths Solutions Chapter 1 Integer enough to prepare for the exams?
Yes, the NCERT Exemplar for Class 7 Maths Solutions Chapter 1 Integers will be enough for you to revise the chapter and prepare for your exam. It contains many questions that you will not find in any other textbook or reference book. There is a high probability of these types of questions appearing in your exams. So, you won’t need any sample papers or previous year question papers to look for questions related to the Class 7 Maths Chapter 1 Integers.
4. Why is it necessary to download the NCERT Exemplar for Class 7 Maths Solutions Chapter 1 Integers PDF?
It is necessary to download the NCERT Exemplar for Class 7 Maths Solutions Chapter 1 Integer PDF as it contains more than a hundred questions. There is a high probability of these types of questions coming in your exams. Since all the concepts of maths require written practice, solving these questions can be helpful for exam preparations. If you get stuck on any of these questions, you can look at the answers to know how to solve them.
5. Does the NCERT Exemplar for Class 7 Maths Solutions Chapter 1 Integers provide answers in detail?
Yes, the NCERT Exemplar for Class 7 Maths Solutions Chapter 1 Integers provides you with detailed answers to all the questions. Even for MCQs, there is an explanation as to why a particular option is right. For very short, short, and long answer type questions, you will find step-by-step solutions to help you understand the answers. It will also show you how you can solve Class 7 Maths Chapter 1 Integers questions in the correct sequence of steps and gain full marks.























