Courses

Courses for Kids

Free study material

Store

Talk to our experts

1800-120-456-456

NCERT Exemplar for Class 11 Maths Chapter 16 - Probability (Book Solutions)

Textbook Solutions

NCERT Exemplar for Class 11 Maths Chapter 16 - Probability (Book Solutions)

NCERT Exemplar for Class 11 Maths - Probability - Free PDF Download

Free PDF download of NCERT Exemplar for Class 11 Maths Chapter 16 - Probability solved by expert Maths teachers on Vedantu.com as per NCERT (CBSE) Book guidelines. All Chapter 16 - Probability exercise questions with solutions to help you to revise the complete syllabus and score more marks in your examinations.

Class 11 Maths, Chapter 16 is Probability in the NCERT Exemplar Solutions and is available on Vedantu for the benefit of students who are preparing for the examinations. It is advised to the students to get well versed with the solutions of the NCERT Exemplar for Class 11 Maths to secure a good score in the Class 11 examination. These NCERT Exemplar problems have been solved by the experts at Vedantu. The solutions will help the students in understanding and mastering different types of questions on the probability that might appear in the exams. The NCERT Exemplar solutions will also help the students attain perfection in solving the different kinds of questions in maths.

The PDF for the NCERT Exemplar Solutions for Class 11 Maths Chapter 16 Probability is provided on Vedantu’s site. The students can refer and download the same from the website. The solutions will facilitate students to enhance their knowledge about the basic Mathematical concepts. The NCERT Exemplar class 11 chapter 16 Probability is based on random experiments and other topics.

Access NCERT Exemplar Solutions for Class 11 Mathematics Chapter 16 - Probability

Examples

Example 1: An ordinary deck of cards contains $52$ cards divided into four suits. The red suits are diamonds and hearts and black suits are clubs and spades. The cards $J$, $Q$ and $K$ are called face cards. Suppose we pick one card from the deck at random.

(a). What is the sample space of the experiment?

Ans: Given: A deck of $52$ cards divided into four suits.

The red suits are diamonds and hearts.

The black suits are clubs and spades.

$J$, $Q$ and $K$ are the face cards.

Here ,find the number of ways to select $1$ card out of a total of $52$ cards in the deck.

Since $1$ card is selected at random from the deck which has a total of $52$ cards, the total number of sample space is the number of ways in which $1$ card can be selected.

Therefore, the number of sample space $= {}^{52}{C_1} = 52$.

(b) What is the event that the chosen card is a black face card?

Ans: Given: A deck of $52$ cards divided into four suits.

The red suits are diamonds and hearts.

The black suits are clubs and spades.

$J$, $Q$ and $K$ are the face cards.

Here, check the number of face cards that are included in the black suit.

Since the face cards are Jacks $\left( J \right)$, Kings $\left( K \right)$ and Queens $\left( Q \right)$. In each suit there is one of each face card.

Two suits (spades and clubs) are black, so the Jacks, Kings and Queens of these two suits are the required event.

Example 2: Suppose that each child born is equally likely to be a boy or a girl. Consider a family with exactly three children.

(a) List the eight elements in the sample space whose outcomes are all possible genders of the three children.

Ans: Given, A family having exactly three children.

Chance of having a girl is equal to the chance of a boy.

Represent a boy with $B$ and a girl with $G$ and form all the combinations that can be made regarding the genders of the three children.

Let us represent a boy with $B$ and a girl with $G$.

The possible combinations of the genders of the three children in the family is given as $\left\{ {BBB,{\text{ }}BBG,{\text{ }}BGB,{\text{ }}GBB,{\text{ }}GGG,{\text{ }}GGB,{\text{ }}GBG,{\text{ }}BGG} \right\}$. There can be a total of $8$ outcomes, so the number of sample spaces is $n\left( S \right) = 8$.

(b) Write each of the following events as a set and find its probability:

(i) The event that exactly one child is a girl.

Ans: Let us find the favourable sample spaces in each subpart.

The event in which there is exactly one girl child is given by $X = \left\{ {BBG,{\text{ }}BGB,{\text{ }}GBB} \right\}$. So the number of favourable elements is $n\left( X \right) = 3$.

Therefore, probability $= \dfrac{{n\left( X \right)}}{{n\left( S \right)}} = \dfrac{3}{8}$.

(ii) The event the at least two children are girls.

Ans: Let us find the favourable sample spaces in each subpart.

The event in which there are at least two girl child is given by $Y = \left\{ {GGG,{\text{ }}GGB,{\text{ }}GBG,{\text{ }}BGG} \right\}$. So the number of favourable elements is $n\left( Y \right) = 4$.

Therefore, probability $= \dfrac{{n\left( Y \right)}}{{n\left( S \right)}} = \dfrac{4}{8} = \dfrac{1}{2}$.

(iii) The event that no child is a girl.

Ans: Let us find the favourable sample spaces in each subpart.

The event in which there is no girl child is given by $Z = \left\{ {BBB} \right\}$. So the number of favourable elements is $n\left( Z \right) = 1$.

Therefore, probability $= \dfrac{{n\left( Z \right)}}{{n\left( S \right)}} = \dfrac{1}{8}$.

Example 3: (a) How many two – digit positive integers are multiple of $3$?

Ans: Consider all the numbers from $10$ to $99$ as the two – digit positive integers. The first integer divisible by $3$ is $12$ and the last is $99$ (among the two digit – integers).

All the integers from $10$ to $99$ are the positive two - digit integers. So, there are $90$ two - digit positive integers. Therefore, the total number of sample spaces is $n\left( S \right) = 90$.

Among all the two – digit positive integers, the multiples of $3$ are $12$, $15$, $18$, …, $99$. So there are a total of $30$ integers that are divisible by $3$. Therefore, the number of favourable sample spaces is $n\left( E \right) = 30$.

(b) What is the probability that a randomly chosen two – digit positive integer is a multiple of $3$?

Ans: Consider all the numbers from $10$ to $99$ as the two – digit positive integers. The first integer divisible by $3$ is $12$ and the last is $99$ (among the two digit – integers).

All the integers from $10$ to $99$ are the positive two – digit integers. So, there are $90$ two – digit positive integers. Therefore, the total number of sample spaces is $n\left( S \right) = 90$.

Hence, the probability of choosing an integer that is a multiple of $3$

$= \dfrac{{n\left( E \right)}}{{n\left( S \right)}}$

$= \dfrac{{30}}{{90}}$

$= \dfrac{1}{3}$

Example 4: A typical PIN (personal identification number) is a sequence of any four symbols chosen from the $26$ letters in the alphabet and the ten digits. If all PINs are equally likely, what is the probability that a randomly chosen PIN contains a repeated symbol?

Ans: Given: A PIN that contains a sequence of any four symbols taken from the $26$ letters of the alphabet and the ten digits.

Find the total number of sample space by considering that each place of the symbol can be filled with $36$ choices (if repetition is allowed).

Now, find the number of combinations that can be made if none of the symbols is repeating. Hence, subtract this from the total number of sample spaces to get the number of favourable sample spaces.

There are $26$ alphabets and $10$ digits, so there are a total of $36$ symbols. If the repetition is allowed then each of the four symbols can be chosen in $36$ ways.

Therefore, the total number of sample spaces is $n\left( S \right) = 36 \times 36 \times 36 \times 36 = 1679616$.

Now, if none of the symbols is repeated then the number of ways in which the four symbols can be filled is $36 \times 35 \times 34 \times 33 = 1413720$.

So the number of combinations if at least one symbol is repeated $= \left( {1679616 - 1413720} \right) = 265896$. These favourable outcomes are $n\left( E \right) = 265896$.

Hence, the required probability $= \dfrac{{265896}}{{1679616}}$.

Example 5: An experiment has four possible outcomes $A$, $B$, $C$ and $D$, that are mutually exclusive. Explain why the following assignments of probabilities are not permissible:

(a) $P\left( A \right) = 0.12$, $P\left( B \right) = 0.63$, $P\left( C \right) = 0.45$, $P\left( D \right) = - 0.20$

Ans: Given: Four mutually exclusive outcomes of an experiment $A$, $B$, $C$ and $D$ and their probabilities to occur.

use the fact that the probability of an event to occur lies in the interval $\left[ {0,1} \right]$.

Here the probability of event $D$ to occur is $P\left( D \right) = - 0.20$ which is negative. The probability of an event to occur is never negative and always lies in the interval $\left[ {0,1} \right]$. Therefore, this assignment of probabilities is not permissible.

(b) $P\left( A \right) = \dfrac{9}{{120}}$, $P\left( B \right) = \dfrac{{45}}{{120}}$, $P\left( C \right) = \dfrac{{27}}{{120}}$, $P\left( D \right) = \dfrac{{46}}{{120}}$

Ans: Given: Four mutually exclusive outcomes of an experiment $A$, $B$, $C$ and $D$ and their probabilities to occur.

use the fact that the sum of all the probabilities of an event in an experiment is $1$.

Here the sum of all the probabilities

$= P\left( A \right) + P\left( B \right) + P\left( C \right) + P\left( D \right)$

$= \dfrac{9}{{120}} + \dfrac{{45}}{{120}} + \dfrac{{27}}{{120}} + \dfrac{{46}}{{120}}$

$= \dfrac{{127}}{{120}}$

The sum of all the probabilities of the events in an experiment is always $1$. Therefore, this assignment of probabilities is not permissible.

Example 6: Probability that a truck stopped at a roadblock will have faulty brakes or badly worn tires are $0.23$ and $0.24$, respectively. Also, the probability is $0.38$ that a truck stopped at the roadblock will have faulty brakes and/or badly working tires. What is the probability that a truck stopped at this roadblock will have faulty brakes as well as badly worn tires?

Ans: Given: Probability that the truck stopped due to faulty brakes $= 0.23$

Probability that the truck stopped due badly worn tires $= 0.24$

Probability that the truck stopped due to faulty brakes and/or badly working tires $= 0.38$

Assume $P\left( A \right)$ and $P\left( B \right)$ as the probabilities that the truck stopped due to faulty brakes and badly worn tires, respectively.

Use the formula $P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {A \cap B} \right)$ to find the value of \[P\left( {A \cap B} \right)\].

Probability that the truck stopped due to faulty brakes $= P\left( A \right) = 0.23$

Probability that the truck stopped due badly worn tires $= P\left( B \right) = 0.24$

Probability that the truck stopped due to faulty brakes and/or badly working tires $P\left( {A \cup B} \right) = 0.38$

Using the formula $P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {A \cap B} \right)$, the probability that the truck stopped de to both faulty brakes and badly worn tires is

$= P\left( {A \cap B} \right)$

$= P\left( A \right) + P\left( B \right) - P\left( {A \cup B} \right)$

$= 0.23 + 0.24 - 0.38$

$= 0.09$

Example 7: If a person visits his dentist, suppose the probability that he will have his teeth cleaned is $0.48$, the probability that he will have a cavity filled is $0.25$, the probability that he will have a tooth extracted is $0.20$, the probability that he will have a teeth cleaned and a cavity filled is $0.09$, the probability that he will have his teeth cleaned and tooth extracted is $0.12$, the probability that he will have a cavity filled and a tooth extracted is $0.07$ and the probability that he will have his teeth cleaned, a cavity filled, and a tooth extracted is $0.03$. What is the probability that a person visiting his dentist will have at least one of these things done to him?

Ans: Given: Probability that the person will: -

get the teeth cleaned $= 0.48$

get the cavity filled $= 0.25$

get the tooth extracted $= 0.20$

get the teeth cleaned and cavity filled $= 0.09$

get the teeth cleaned and tooth extracted $= 0.12$

get the cavity filled and tooth extracted $= 0.07$

get the teeth cleaned, tooth extracted and cavity filled $= 0.03$

Assume the probabilities of the person getting his teeth cleaned, cavity filled and tooth extracted as $P\left( A \right)$, $P\left( B \right)$ and $P\left( C \right)$ respectively.

Use the formula $P\left( {A \cup B \cup C} \right) = P\left( A \right) + P\left( B \right) + P\left( C \right) - P\left( {A \cap B} \right) - P\left( {B \cap C} \right) - P\left( {A \cap C} \right) + P\left( {A \cap B \cap C} \right)$ to solve for the value of $L.H.S$.

Let us assume the probabilities of the person getting his teeth cleaned, cavity filled and tooth extracted as $P\left( A \right)$, $P\left( B \right)$ and $P\left( C \right)$ respectively. Therefore, according to the question,

$P\left( A \right) = 0.48$, $P\left( B \right) = 0.25$, $P\left( C \right) = 0.20$

$P\left( {A \cap B} \right) = 0.09$, $P\left( {B \cap C} \right) = 0.12$, $P\left( {A \cap C} \right) = 0.07$

$P\left( {A \cap B \cap C} \right) = 0.03$

Therefore, the probability of the person getting at least one the three things done to his is $P\left( {A \cup B \cup C} \right)$ which is

$= P\left( A \right) + P\left( B \right) + P\left( C \right) - P\left( {A \cap B} \right) - P\left( {B \cap C} \right) - P\left( {A \cap C} \right) + P\left( {A \cap B \cap C} \right)$

$= 0.48 + 0.25 + 0.20 - 0.09 - 0.12 - 0.07 + 0.03$

$= 0.68$

Example 8: An urn contains twenty white slips of paper numbered from 1 through $20$, ten red slips of paper numbered from $1$ through $10$, forty yellow slips of paper numbered from $1$ through $40$, and ten blue slips of paper numbered from $1$ through $10$. If these $80$ slips of paper are thoroughly shuffled so that each slip has the same probability of being drawn. Find the probabilities of drawing a slip of paper that is:

(a) Blue or white.

Ans: Given: Number of white slips $= 20$

Number of red slips $= 10$

Number of yellow slips $= 40$

Number of blue slips $= 10$

Find the total number of favourable slips that are satisfying the conditions in each case one by one.

The total number of slips is the total number of sample spaces $n\left( S \right) = 80$.

There are $20$ white slips and $10$ blue slips and any one can be chosen. So the number of favourable sample spaces is $n\left( A \right) = 20 + 10 = 30$.

Therefore, the required probability

$= \dfrac{{n\left( A \right)}}{{n\left( S \right)}}$

$= \dfrac{{30}}{{80}}$

$= \dfrac{3}{8}$

(b) Numbered $1$, $2$, $3$, $4$ or $5$.

Ans: Given: Number of white slips $= 20$

Number of red slips $= 10$

Number of yellow slips $= 40$

Number of blue slips $= 10$

Find the total number of favourable slips that are satisfying the conditions in each case one by one.

The total number of slips is the total number of sample spaces $n\left( S \right) = 80$.

In each set of the coloured papers there are five papers numbered $1$, $2$, $3$, $4$ or $5$. So the total number of papers satisfying the condition is $n\left( B \right) = \left( {5 + 5 + 5 + 5} \right) = 20$.

Therefore, the required probability

$= \dfrac{{n\left( B \right)}}{{n\left( S \right)}}$

$= \dfrac{{20}}{{80}}$

$= \dfrac{1}{4}$

Ans: Given: Number of white slips $= 20$

Number of red slips $= 10$

Number of yellow slips $= 40$

Number of blue slips $= 10$

Find the total number of favourable slips that are satisfying the conditions in each case one by one.

The total number of slips is the total number of sample spaces $n\left( S \right) = 80$.

There are four papers each in the sets of both red and yellow coloured papers numbered $1$, $2$, $3$ or $4$. So the total number of papers satisfying the condition is $n\left( C \right) = \left( {4 + 4} \right) = 8$.

Therefore, the required probability

$= \dfrac{{n\left( C \right)}}{{n\left( S \right)}}$

$= \dfrac{8}{{80}}$

$= \dfrac{1}{{10}}$

(d) Numbered $5$, $15$, $25$ or $35$.

Ans: Given: Number of white slips $= 20$

Number of red slips $= 10$

Number of yellow slips $= 40$

Number of blue slips $= 10$

Find the total number of favourable slips that are satisfying the conditions in each case one by one.

The total number of slips is the total number of sample spaces $n\left( S \right) = 80$.

The number $5$ paper is present in all the four sets of paper, the number $15$ paper is present in only white and yellow slips and the number $25$ and number $35$ paper is present only in the yellow set of paper. So the total number of papers satisfying the condition is $n\left( D \right) = \left( {4 + 2 + 1 + 1} \right) = 8$.

Therefore, the required probability

$= \dfrac{{n\left( D \right)}}{{n\left( S \right)}}$

$= \dfrac{8}{{80}}$

$= \dfrac{1}{{10}}$

(e) White and numbered higher than $12$ or yellow and numbered higher than $26$.

Ans: Given: Number of white slips $= 20$

Number of red slips $= 10$

Number of yellow slips $= 40$

Number of blue slips $= 10$

Find the total number of favourable slips that are satisfying the conditions in each case one by one.

The total number of slips is the total number of sample spaces $n\left( S \right) = 80$.

The are $8$ white slips numbered greater than $12$ and $14$ yellow slips numbered greater than $26$. So the total number of papers satisfying the condition is $n\left( E \right) = \left( {8 + 14} \right) = 22$.

Therefore, the required probability

$= \dfrac{{n\left( E \right)}}{{n\left( S \right)}}$

$= \dfrac{{22}}{{80}}$

$= \dfrac{{11}}{{40}}$

Objective Type Questions:

Choose the correct answer from given four options in each of the Examples 9 to 15 (M.C.Q.):

Example 9: In a leap year the probability of having $53$ Sundays or $53$ Mondays is

(A) $\dfrac{2}{7}$

(B) $\dfrac{3}{7}$

(D) $\dfrac{5}{7}$

Ans: Normal year has $365$ days and $52$ weeks and $1$ day. And a leap year has $366$ days and hence $52$

weeks and $2$ days. Then possibilities of other $2$ days can be

1. Sunday, Monday

2. Monday, Tuesday

3. Tuesday, Wednesday

4. Wednesday, Thursday

5. Thursday, Friday

6. Friday, Saturday

7. Saturday, Sunday

Therefore, considering two events ${{P}}\left( {{A}} \right)$ and ${{P}}\left( {\text{B}} \right)$

Where, ${{P}}\left( {{A}} \right)$$=$ the leap year that contains $53$ Sundays

${{P}}\left( {{B}} \right)$$=$ the leap year that contains $53$ Mondays

${{P}}\left( {{{A}} \cap {\text{B}}} \right)$$=$ Probability that Sunday and Monday occur simultaneously

So, there are $7$ possibilities of $53$ Sundays or $53$ Mondays

$\therefore {{n}}\left( {\text{S}} \right) = 7$

${{P}}\left( {{A}} \right)$$=$$2$

${{P}}\left( {{B}} \right)$$=$$2$

Now,

${{P}}\left( {{{A}} \cup {{B}}} \right) = {\text{P}}\left( {{A}} \right) + {{P}}\left( {{B}} \right) - {{P}}\left( {{{A}} \cap {{B}}} \right)$

$= \dfrac{2}{7} + \dfrac{2}{7} - \dfrac{1}{7}$

$= \dfrac{{2 + 2 - 1}}{7}$

$= \dfrac{3}{7}$

Hence, the probability of $53$ Sundays or $53$ Mondays is $\dfrac{3}{7}$

Correct Answer: B

Example 10: Three digit numbers are formed using the digits 0, 2, 4, 6, 8. A number is

chosen at random out of these numbers. What is the probability that this number has

the same digits?

(A) $\dfrac{1}{{16}}$

(B) $\dfrac{{16}}{{25}}$

(D) \[\dfrac{1}{{25}}\]

Ans: $3$-digit number cannot start with digit $0$, but hundredth can have any of the $4$digits other than $0$. Now, all $5$ digits can be placed at unit and tens place then total possible $3$-digit numbers are \[4{\text{ }} \times {\text{ }}5{\text{ }} \times {\text{ }}5\] i.e., $100$.

$\therefore {{n}}\left( {{S}} \right) = 100$

The total possible $3$-digit number having all digits same \[ = 4\] i.e., ${{n}}\left( {\text{E}} \right)$

Hence, Probability of $3$-digit number with same digits $= \dfrac{{{{n}}\left( {{E}} \right)}}{{{{n}}\left( {{S}} \right)}}$

$= \dfrac{4}{{100}}$

$ = \dfrac{1}{{25}}$

Correct Answer: D

Example 11: Three squares of chess board are selected at random. The probability of getting $2$ squares of one colour and other of a different colour is:

(A) $\dfrac{{16}}{{21}}$

(B) $\dfrac{8}{{21}}$

(D) $\dfrac{3}{8}$

Ans: A chess board has $64$ squares in which $32$ are Black and $32$ are White. Now, as per the question $3$ squares are to be selected in which $2$ can be of single colour and $1$can be of other colour so they can be selected in either of the two ways i.e., $\left( {2{\text{white or}}1{\text{black}}} \right)$ OR $\left( {1{\text{white or}}2{\text{black}}} \right)$ then these can be selected as:

$^{32}{{\text{C}}_2} \times {^{32}}{{\text{C}}_1} \times 2$

Now the $3$ squares selected randomly is in $^{64}{{\text{C}}_3}$ way

$\therefore {\text{n}}\left( {\text{E}} \right) =$$^{32}{{\text{C}}_2} \times {^{32}}{{\text{C}}_1} \times 2$

And ${\text{n}}\left( {\text{S}} \right) =$$^{64}{{\text{C}}_3}$

So, ${\text{P}}\left( {\text{E}} \right) = \dfrac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right)}}$

$= \dfrac{{^{32}{{\text{C}}_2} \times {^{32}}{{\text{C}}_1} \times 2}}{{^{64}{{\text{C}}_3}}}$

$= \dfrac{{16}}{{21}}$

Hence, probability is $\dfrac{{16}}{{21}}$

Correct Answer: A

Example 12: If ${\text{A}}$ and ${\text{B}}$ are any two events having $P\left( {A\cup B} \right) = \dfrac{1}{2}$ and $P\left( {\bar A} \right) = \dfrac{2}{3}$ then the probability of \[\bar{A} \cap B\] is:

(A) $\dfrac{1}{2}$

(B) \[\dfrac{2}{3}\]

(D) $\dfrac{1}{3}$

Ans: We know, ${\text{P}}\left( {{\text{A}} \cup {\text{B}}} \right) = {\text{P}}\left( {\text{A}} \right) + {\text{P}}\left( {\text{B}} \right) - {\text{P}}\left( {{\text{A}} \cap {\text{B}}} \right)$

And ${\text{P}}\left( {\text{A}} \right) = 1 - {\text{P}}\left( {{{\bar A}}} \right)$

Given ${\text{P}}\left( {{\text{A}} \cup {\text{B}}} \right) = \dfrac{1}{2}$ and ${\text{P}}\left( {{{\bar A}}} \right) = \dfrac{2}{3}$

${\text{P}}\left( {\text{A}} \right) = 1 - \dfrac{2}{3} = \dfrac{1}{3}$

Therefore,

⇒${\text{P}}\left( {{\text{A}} \cup {\text{B}}} \right) = {\text{P}}\left( {\text{A}} \right) + {\text{P}}\left( {\text{B}} \right) - {\text{P}}\left( {{\text{A}} \cap {\text{B}}} \right)$

$\dfrac{1}{2} = \dfrac{1}{3} + {\text{P}}\left( {\text{B}} \right) - {\text{P}}\left( {{\text{A}} \cap {\text{B}}} \right)$

${\text{P}}\left( {\text{B}} \right) - {\text{P}}\left( {{\text{A}} \cap {\text{B}}} \right) = \dfrac{1}{6}$

And

Then, ${\text{P}}\left( {{{\bar A}} \cap {\text{B}}} \right) = \dfrac{1}{6}$

\[\left( {{\text{since A}} \cap {\text{ B}} \equiv {\text{ B}}-{\text{A}}} \right)\]

Correct Answer: C

Example 13: Three of the six vertices of a regular hexagon are chosen at random. What is the probability that the triangle with these vertices is equilateral?

(A) $\dfrac{3}{{10}}$

(B) $\dfrac{3}{{20}}$

(D) $\dfrac{1}{{10}}$

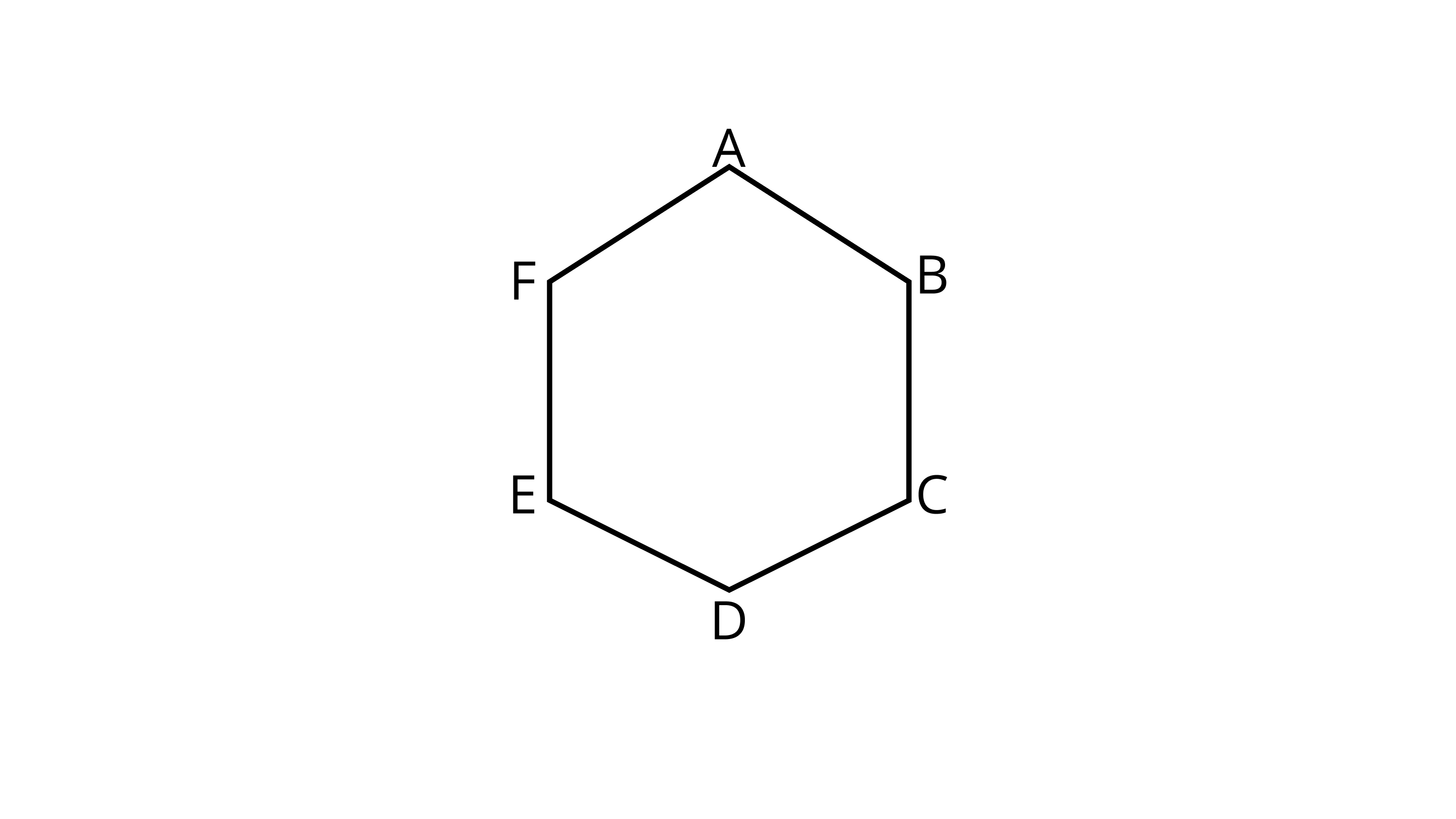
Ans: Regular hexagon ${\text{ABCDEF}}$

Then, total number of triangles are $^6{{\text{C}}_3}$

$= \dfrac{{6!}}{{3!\left( {6 - 3} \right)!}}$

$= \dfrac{{120}}{6} = 20$

Because there are no three collinear points there are only two equilateral triangles i.e., $\vartriangle {\text{ACF}}$ and $\vartriangle {\text{BDF}}$

$\therefore {\text{n}}\left( {\text{E}} \right) = 2$

${\text{n}}\left( {\text{S}} \right) = 20$

Therefore, required probability, ${\text{P}}\left( {{E}} \right) = \dfrac{{{{n}}\left( {\text{E}} \right)}}{{{{n}}\left( {{S}} \right)}}$

$= \dfrac{2}{{20}} = \dfrac{1}{{10}}$

Correct Answer: D

Example 14: If $A,B, C$ are three mutually exclusive and exhaustive events of an experiment such that \[3P\left( A \right) = 2P\left( B \right) = P\left( C \right)\] then $P\left( A \right)$ is equal to

(A) $\dfrac{1}{{11}}$

(B) $\dfrac{2}{{11}}$

(D) $\dfrac{6}{{11}}$

Ans: Given, \[3{\text{P}}\left( {\text{A}} \right) = 2{\text{P}}\left( {\text{B}} \right) = {\text{P}}\left( {\text{C}} \right)\]

Let \[3{\text{P}}\left( {\text{A}} \right) = 2{\text{P}}\left( {\text{B}} \right) = {\text{P}}\left( {\text{C}} \right) = x\]

Then,

${\text{P}}\left( {\text{A}} \right) = \dfrac{x}{3}$

${\text{P}}\left( {\text{B}} \right) = \dfrac{x}{2}$

And ${\text{P}}\left( {\text{C}} \right) = x$

$\therefore {\text{P}}\left( {\text{A}} \right) + {\text{P}}\left( {\text{B}} \right) + {\text{P}}\left( {\text{C}} \right) = 1$

$\Rightarrow \dfrac{x}{3} + \dfrac{x}{2} + x = 1$

$\Rightarrow \dfrac{{2x + 3x + 6x}}{6} = 1$

$\dfrac{{11x}}{6} = 1$

$x = \dfrac{6}{{11}}$

$\because {\text{P}}\left( {\text{A}} \right) = \dfrac{x}{3}$

Then, ${\text{P}}\left( {\text{A}} \right) = \dfrac{x}{3} = \dfrac{6}{{11}} \times \dfrac{1}{3} = \dfrac{2}{{11}}$

Hence, ${\text{P}}\left( {\text{A}} \right) = \dfrac{2}{{11}}$

Correct Answer: B

Example 15: One mapping (function) is selected at random from all the mappings of the set \[A = \left\{ {1,2,3,..., n} \right\}\] into itself. The probability that the mapping selected is one to one is

(A) $\dfrac{1}{{{n^n}}}$

(B) $\dfrac{1}{n!}$

(D) none of these

Ans: $\left( {{\text{with }} n{\text{ elements}}} \right)$ number of mapping for set ${\text{A}}$$= {n^n}$

And, the number of $1{\text{to}}{\text{1}}$ mapping for the set ${\text{A}}$ itself is $n!$

So, the probability is $= \dfrac{{n!}}{{{n^n}}} = \dfrac{{\left( {n - 1} \right)!}}{{{n^{n - 1}}}}$

Correct Answer: C

Long Type Question

Exercise:

1: If the letters of the word ALGORITHM are arranged in a row, what is the probability the letters GOR must remain together.

Ans: Given: The letters of the word ALGORITHM are arranged.

Find the total number of sample spaces by finding the number of words that can be formed with the given letters of the word.

Now, find the favourable number of arrangements by considering the letters GOR always together.

There are $9$ different letters in the word ALGORITHM, so the total number of words that can be formed is the number of sample spaces $n\left( S \right) = 9!$.

Now, the letters GOR always remain together. These can be considered as a single unit, so the remaining $6$ letters and this single unit makes a total of $7$ things which can be arranged in $7!$ ways.

So the number of favourable arrangements is $n\left( E \right) = 7!$.

Hence, the required probability

$= \dfrac{{n\left( S \right)}}{{n\left( E \right)}}$

$= \dfrac{{7!}}{{9!}}$

$= \dfrac{1}{{72}}$

2. Six new employees, two of whom are married to each other, are to be assigned six desks that are lined up in a row. If the assignment of employees to desks is made randomly, what is the probability that the married couple will have non-adjacent desks?

Ans: Given: Total number of new employees $= 6$

Total number of desks in the assigned row $= 6$

A married couple is present among the $6$ employees.

Find the total number of sample space by arranging all the six employees without any condition.

Now, find the number of arrangements in which the couple always gets the adjacent seat. Subtract it from the total number of sample spaces to get the favourable sample spaces.

The $6$ new employees can be arranged at $6$ desks (without any condition) in $6!$ ways, so the number of sample space is $n\left( S \right) = 6!$.

Let us consider that the couple gets the adjacent seat, so the two people in this couple can be arranged among themselves in $2!$ ways. This couple can be considered as a single unit, so the remaining four employees and this single unit can be considered as $5$ things which can be arranged in $5!$ ways.

The total number of arrangements where the couple is always together $= 2!{\text{ }} \times {\text{ }}5!$.

Therefore, the number of arrangements where the coupe in never together $n\left( E \right) = 6!{\text{ }} - {\text{ }}\left( {2!{\text{ }} \times {\text{ }}5!} \right)$.

Hence, the required probability

$= \dfrac{{n\left( E \right)}}{{n\left( S \right)}}$

$= \dfrac{{6!{\text{ }} - \left( {2!{\text{ }} \times {\text{ }}5!} \right)}}{{6!}}$

$= \dfrac{2}{3}$

3. Suppose an integer from $1$ to $1000$ is chosen at random, find the probability that the integer is a multiple of $2$ or a multiple of $9$.

Ans: Given: An integer from $1$ to $1000$ is chosen at random.

Find the total number of sample space by selecting any one integer out of a total of $1000$ integers given.

Find the numbers that are divisible by $2$ or $9$ and count the number of integers which are divisible by both to get the favourable sample spaces.

The total number of integers is from $1$ to $1000$ is thousand, so the number of ways in which one can be selected is the total number of sample space $n\left( S \right) = {}^{1000}{C_1}$.

Now, all the even integers are divisible by $2$, so there will be $500$ even numbers from $1$ to $1000$ and any one of them can be selected in ${}^{500}{C_1}$ ways. The integers that are divisible by $9$ are $9$, $18$, $27$, $36$, …, $999$. There are $111$ such integers divisible by $9$.

Among these $111$ integers there will be integers like $18$, $36$, $54$, … etc. which are also divisible by $2$ and they are already considered earlier. There are $55$ such integers. So the number of integers that is to be considered is $\left( {111 - 55} \right) = 56$ and any one of them can be chosen in ${}^{56}{C_1}$ ways.

Therefore, the number of favourable sample spaces $n\left( E \right) = {}^{500}{C_1} + {}^{56}{C_1}$.

Hence, the required probability is

$= \dfrac{{n\left( E \right)}}{{n\left( S \right)}}$

$= \dfrac{{{}^{500}{C_1} + {}^{56}{C_1}}}{{{}^{1000}{C_1}}}$

$= 0.556$

4: An experiment consists of rolling a die until a $2$ appears.

(i) How many elements of the sample space correspond to the event that $2$ appears on the ${k^{th}}$ roll of the die?

Ans: Given: A die is rolled until a $2$ appears.

consider that the first $\left( {k - 1} \right)$ rolls of the die results in any of the five outcomes except $2$.

There are $6$ outcomes when a die is rolled.

In this case $2$ appears on the ${k^{th}}$ roll, so in the first $\left( {k - 1} \right)$ roll there are $5$ possible outcomes other than $2$ on each roll.

Therefore, the number of elements $= 5 \times 5 \times 5 \times 5 \times ...\left( {k - 1} \right){\text{ times}} = {5^{k - 1}}$.

(ii) How many elements of the sample space correspond to the event that $2$ appears not later than the ${k^{th}}$ roll of the die?

Ans: Given: A die is rolled until a $2$ appears.

consider different situations where $2$ may appear in the first or second or third time etc. Add the number of elements of different situations.

In this case $2$ appears before the ${k^{th}}$ roll, so it may appear on the first roll or second roll or third role or … ${\left( {k - 1} \right)^{th}}$ roll.

If it appears on the first roll then the number of elements $= 1$.

If it appears on the second roll that means in the first roll there are $5$ outcomes and in the second role $1$, so the number of elements $= 5 \times 1$.

If it appears on the third roll that means in the first two rolls there are $5$ outcomes each and in the third role $1$, so the number of elements $= 5 \times 5 \times 1$.

Observing the pattern, the number of elements in $\left( {k - 1} \right)$ rolls $= 5 \times 5 \times 5 \times 5 \times ...\left( {k - 1} \right){\text{ times}} \times 1$.

Hence, the total number of elements of all the different situations = $1 + 5 + {5^2} + {5^3} + {...5^{\left( {k - 1} \right)}}$.

This is a geometric progression whose sum of the terms $= \left( {\dfrac{{{5^k} - 1}}{4}} \right)$.

5. A die is loaded in such a way that each odd number is twice as likely to occur as each even number. Find $P\left( G \right)$, where $G$ is the event that a number greater than $3$ occurs on a single roll of the die.

Ans: Given: Number of times the die is rolled $= 1$

Probability of occurrence of an odd number is twice that of an even number.

$G$ is the event of occurrence of a number greater than $3$ on a single roll.

Find the total number of sample spaces when a die is rolled. Consider the odd numbers likely to occur twice.

Find the favourable sample spaces by considering the numbers $4$, $5$ or $6$ to occur.

When a die is rolled the number of outcomes is $6$ which are $\left\{ {1,{\text{ }}2,{\text{ }}3,{\text{ }}4,{\text{ }}5,{\text{ }}6} \right\}$. It is said that each odd number is likely to occur twice of the occurrence of each even number.

So the sample spaces can be $\left\{ {1,{\text{ }}1,{\text{ }}2,{\text{ }}3,{\text{ }}3,{\text{ }}4,{\text{ }}5,{\text{ }}5,{\text{ }}6} \right\}$. Here $n\left( S \right) = 9$.

The numbers greater than $3$ are $4$, $5$ and $6$, so the favourable sample spaces to occur are $\left\{ {4,{\text{ }}5,{\text{ }}5,{\text{ }}6} \right\}$. Here $n\left( E \right) = 4$.

Hence, the required probability $P\left( G \right) = \dfrac{{n\left( S \right)}}{{n\left( E \right)}} = \dfrac{4}{9}$.

6. In a large metropolitan area, the probabilities are $0.87$, $0.36$, $0.30$ that a family (randomly chosen for a sample survey) owns a colour television set, a black and white television set, or both kinds of sets. What is the probability that a family owns either anyone or both kinds of sets?

Ans: Given: Probability that the chosen family owns a colour television set $= 0.87$

Probability that the chosen family owns a black and white television set $= 0.36$

Probability that the chosen family owns both the sets $= 0.30$

Assume $P\left( C \right)$ and $P\left( B \right)$ as the probabilities that the chosen family owns a colour television set and a black and white television set respectively.

Use the formula $P\left( {B \cup C} \right) = P\left( B \right) + P\left( C \right) - P\left( {B \cap C} \right)$.

Probability that the chosen family owns a colour television set $= P\left( C \right) = 0.87$.

Probability that the chosen family owns a black and white television set $= P\left( B \right) = 0.36$.

Probability that the chosen family owns both the sets $= P\left( {B \cap C} \right) = 0.30$.

Using the formula $P\left( {B \cup C} \right) = P\left( B \right) + P\left( C \right) - P\left( {B \cap C} \right)$, the probability that the chosen family owns either anyone or both kinds of sets

$= P\left( {B \cup C} \right)$

$= P\left( B \right) + P\left( C \right) - P\left( {B \cap C} \right)$

$= 0.87 + 0.36 - 0.30$

$= 0.93$

7. If $A$ and $B$ are mutually exclusive events, $P\left( A \right) = 0.35$, $P\left( B \right) = 0.45$, find

$\left( a \right)P\left( {A'} \right)$

Ans: Given: Two mutually exclusive events $A$ and $B$.

$P\left( A \right) = 0.35$

$P\left( B \right) = 0.45$

Use the formulas: -

$P\left( {A'} \right) = 1 - P\left( A \right)$

$P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {A \cap B} \right)$

$P\left( {A \cap B} \right) = 0$ (for mutually exclusive events)

$P\left( {A \cap B'} \right) = P\left( A \right) - P\left( {A \cap B} \right)$

$P\left( {A' \cap B'} \right) = P\left( {A \cup B} \right)'$

Here $P\left( {A'} \right)$ means the probability that the event $A$ does not occur.

$\Rightarrow P\left( {A'} \right) = 1 - P\left( A \right)$

$\Rightarrow P\left( {A'} \right) = 1 - 0.35$

$\Rightarrow P\left( {A'} \right) = 0.65$

$\left( b \right)P\left( {B'} \right)$

Ans: Given: Two mutually exclusive events $A$ and $B$.

$P\left( A \right) = 0.35$

$P\left( B \right) = 0.45$

Use the formulas: -

$P\left( {A'} \right) = 1 - P\left( A \right)$

$P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {A \cap B} \right)$

$P\left( {A \cap B} \right) = 0$ (for mutually exclusive events)

$P\left( {A \cap B'} \right) = P\left( A \right) - P\left( {A \cap B} \right)$

$P\left( {A' \cap B'} \right) = P\left( {A \cup B} \right)'$

Here $P\left( {B'} \right)$ means the probability that the event $B$ does not occur.

$\Rightarrow P\left( {B'} \right) = 1 - P\left( B \right)$

$\Rightarrow P\left( {B'} \right) = 1 - 0.45$

$\Rightarrow P\left( {B'} \right) = 0.55$

$\left( c \right)P\left( {A\cup B} \right)$

Ans: Given: Two mutually exclusive events $A$ and $B$.

$P\left( A \right) = 0.35$

$P\left( B \right) = 0.45$

Use the formulas: -

$P\left( {A'} \right) = 1 - P\left( A \right)$

$P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {A \cap B} \right)$

$P\left( {A \cap B} \right) = 0$ (for mutually exclusive events)

$P\left( {A \cap B'} \right) = P\left( A \right) - P\left( {A \cap B} \right)$

$P\left( {A' \cap B'} \right) = P\left( {A \cup B} \right)'$

Here $P\left( {A \cup B} \right)$ is the probability of occurrence of either $A$ or $B$. Using the formula $P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {A \cap B} \right)$, where $P\left( {A \cap B} \right)$ is the probability of occurrence of $A$ and $B$ simultaneously.

$\Rightarrow P\left( {A \cup B} \right) = 0.45 + 0.35 - P\left( {A \cap B} \right)$

$\Rightarrow P\left( {A \cup B} \right) = 0.80 - P\left( {A \cap B} \right)$

Since the events $A$ and $B$ are mutually exclusive that means they cannot occur simultaneously. So $P\left( {A \cap B} \right) = 0$.

$\Rightarrow P\left( {A \cup B} \right) = 0.80$

$\left( d \right)P\left( {A \cap B} \right)$

Ans: Given: Two mutually exclusive events $A$ and $B$.

$P\left( A \right) = 0.35$

$P\left( B \right) = 0.45$

Use the formulas: -

$P\left( {A'} \right) = 1 - P\left( A \right)$

$P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {A \cap B} \right)$

$P\left( {A \cap B} \right) = 0$ (for mutually exclusive events)

$P\left( {A \cap B'} \right) = P\left( A \right) - P\left( {A \cap B} \right)$

$P\left( {A' \cap B'} \right) = P\left( {A \cup B} \right)'$

Since the events $A$ and $B$ are mutually exclusive that means they cannot occur simultaneously. So $P\left( {A \cap B} \right) = 0$.

$\left( e \right)P\left( {A \cap B'} \right)$

Ans: Given: Two mutually exclusive events $A$ and $B$.

$P\left( A \right) = 0.35$

$P\left( B \right) = 0.45$

Use the formulas: -

$P\left( {A'} \right) = 1 - P\left( A \right)$

$P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {A \cap B} \right)$

$P\left( {A \cap B} \right) = 0$ (for mutually exclusive events)

$P\left( {A \cap B'} \right) = P\left( A \right) - P\left( {A \cap B} \right)$

$P\left( {A' \cap B'} \right) = P\left( {A \cup B} \right)'$

Using the formula $P\left( {A \cap B'} \right) = P\left( A \right) - P\left( {A \cap B} \right)$,

$\Rightarrow P\left( {A \cap B'} \right) = 0.35 - 0$

$\Rightarrow P\left( {A \cap B'} \right) = 0.35$

$\left( f \right)P\left( {A' \cap B'} \right)$

Ans: Given: Two mutually exclusive events $A$ and $B$.

$P\left( A \right) = 0.35$

$P\left( B \right) = 0.45$

Use the formulas: -

$P\left( {A'} \right) = 1 - P\left( A \right)$

$P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {A \cap B} \right)$

$P\left( {A \cap B} \right) = 0$ (for mutually exclusive events)

$P\left( {A \cap B'} \right) = P\left( A \right) - P\left( {A \cap B} \right)$

$P\left( {A' \cap B'} \right) = P\left( {A \cup B} \right)'$

Using the formula $P\left( {A' \cap B'} \right) = P\left( {A \cup B} \right)'$,

$\Rightarrow P\left( {A' \cap B'} \right) = 1 - P\left( {A \cup B} \right)$

$\Rightarrow P\left( {A' \cap B'} \right) = 1 - 0.80$

$\Rightarrow P\left( {A' \cap B'} \right) = 0.20$

8. A team of medical students doing their internship have to assist during surgeries at a city hospital. The probabilities of surgeries rated as very complex, complex, routine, simple, very simple are respectively, $0.15$, $0.20$, $0.31$, $0.26$, $0.08$. Find the probabilities that a particular surgery will be rated

(a) Complex or very complex.

Ans: Given: Probabilities that the surgery is very complex $= 0.15$

Probabilities that the surgery is complex $= 0.20$

Probabilities that the surgery is routine $= 0.31$

Probabilities that the surgery is simple $= 0.26$

Probabilities that the surgery is very simple $= 0.08$

Assume $P\left( A \right)$, $P\left( B \right)$, $P\left( C \right)$, $P\left( D \right)$ and $P\left( E \right)$ as the probabilities of different surgeries. Use the formulas of set theory to find the probabilities of different combinations.

Assuming $P\left( A \right)$, $P\left( B \right)$, $P\left( C \right)$, $P\left( D \right)$ and $P\left( E \right)$ as the probabilities of surgeries rated very complex, complex, routine, simple and very simple respectively. All the events are mutually exclusive that means no two of them can occur simultaneously.

Probability that a particular surgery is rated complex or very complex is $P\left( {A \cup B} \right)$.

$\Rightarrow P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {A \cap B} \right)$

$\Rightarrow P\left( {A \cup B} \right) = 0.15 + 0.20 - 0$

$\Rightarrow P\left( {A \cup B} \right) = 0.35$

(b) Neither very complex nor very simple.

Ans: Given: Probabilities that the surgery is very complex $= 0.15$

Probabilities that the surgery is complex $= 0.20$

Probabilities that the surgery is routine $= 0.31$

Probabilities that the surgery is simple $= 0.26$

Probabilities that the surgery is very simple $= 0.08$

Probability that a particular surgery is rated neither very complex nor very simple is $P\left( {A' \cap E'} \right)$.

$\Rightarrow P\left( {A' \cap E'} \right) = 1 - P\left( {A \cup E} \right)$

$\Rightarrow P\left( {A' \cap E'} \right) = 1 - \left( {P\left( A \right) + P\left( E \right) - P\left( {A \cap E} \right)} \right)$

$\Rightarrow P\left( {A' \cap E'} \right) = 1 - \left( {0.15 + 0.08 - 0} \right)$

$\Rightarrow P\left( {A' \cap E'} \right) = 0.77$

Ans: Given: Probabilities that the surgery is very complex $= 0.15$

Probabilities that the surgery is complex $= 0.20$

Probabilities that the surgery is routine $= 0.31$

Probabilities that the surgery is simple $= 0.26$

Probabilities that the surgery is very simple $= 0.08$

Probability that a particular surgery is rated routine or complex is $P\left( {B \cup C} \right)$.

$\Rightarrow P\left( {B \cup C} \right) = P\left( B \right) + P\left( C \right) - P\left( {B \cap C} \right)$

$\Rightarrow P\left( {B \cup C} \right) = 0.20 + 0.31 - 0$

$\Rightarrow P\left( {B \cup C} \right) = 0.51$

(d) Routine or simple

Ans: Given: Probabilities that the surgery is very complex $= 0.15$

Probabilities that the surgery is complex $= 0.20$

Probabilities that the surgery is routine $= 0.31$

Probabilities that the surgery is simple $= 0.26$

Probabilities that the surgery is very simple $= 0.08$

Probability that a particular surgery is rated routine or simple is $P\left( {C \cup D} \right)$.

$\Rightarrow P\left( {C \cup D} \right) = P\left( C \right) + P\left( D \right) - P\left( {C \cap D} \right)$

$\Rightarrow P\left( {C \cup D} \right) = 0.31 + 0.26 - 0$

$\Rightarrow P\left( {C \cup D} \right) = 0.57$

9: Four candidates $A$, $B$, $C$, $D$ have applied for the assignment to coach a school cricket team. If $A$ is twice as likely to be selected as $B$, $B$ and $C$ are given about the same chance of being selected, while $C$ is twice as likely to be selected as $D$, what are the probabilities that

(a) $C$ will be selected?

Ans: Given: Total number of candidates $= 4\left\{ {A,{\text{ }}B,{\text{ }}C,{\text{ }}D} \right\}$

Probability of selection of $A =$$2 \times$ Probability of selection of $B$

Probability of selection of $B =$ Probability of selection of $C$

Probability of selection of $C =$$2 \times$ Probability of selection of $D$

Assume $P\left( A \right)$, $P\left( B \right)$, $P\left( C \right)$ and $P\left( D \right)$ as the probabilities of selection of the given candidates. Form relations between them and use the formula $P\left( A \right) + P\left( B \right) + P\left( C \right) + P\left( D \right) = 1$ to find their values.

Assuming $P\left( A \right)$, $P\left( B \right)$, $P\left( C \right)$ and $P\left( D \right)$ as the probabilities of selection of the candidates $A$, $B$, $C$ and $D$ respectively. All the events are mutually exclusive that means no two of them can occur simultaneously.

According to the information given,

$P\left( A \right) = 2P\left( B \right)$ … (1)

$P\left( B \right) = P\left( C \right)$ … (2)

$P\left( C \right) = 2P\left( D \right)$ … (3)

Using the formula $P\left( A \right) + P\left( B \right) + P\left( C \right) + P\left( D \right) = 1$ and solving the three equations,

$P\left( A \right) = \dfrac{4}{9}$, $P\left( B \right) = \dfrac{2}{9}$, $P\left( C \right) = \dfrac{2}{9}$ and $P\left( D \right) = \dfrac{1}{9}$

Probability that $C$ will be selected is $P\left( C \right) = \dfrac{2}{9}$.

(b) $A$ will not be selected?

Ans: Given: Total number of candidates $= 4\left\{ {A,{\text{ }}B,{\text{ }}C,{\text{ }}D} \right\}$

Probability of selection of $A =$ $2 \times$ Probability of selection of $B$

Probability of selection of $B =$ Probability of selection of $C$

Probability of selection of $C =$ $2 \times$ Probability of selection of $D$

According to the information given,

$P\left( A \right) = 2P\left( B \right)$ … (1)

$P\left( B \right) = P\left( C \right)$ … (2)

$P\left( C \right) = 2P\left( D \right)$ … (3)

Using the formula $P\left( A \right) + P\left( B \right) + P\left( C \right) + P\left( D \right) = 1$ and solving the three equations,

$P\left( A \right) = \dfrac{4}{9}$, $P\left( B \right) = \dfrac{2}{9}$, $P\left( C \right) = \dfrac{2}{9}$ and $P\left( D \right) = \dfrac{1}{9}$

Probability that $A$ will not be selected is $P\left( {A'} \right) = 1 - P\left( A \right)$.

$\Rightarrow P\left( {A'} \right) = 1 - \dfrac{4}{9}$

$\Rightarrow P\left( {A'} \right) = \dfrac{5}{9}$

10. One of the four persons John, Rita, Aslam or Gurpreet will be promoted next month. Consequently the sample space consists of four elementary outcomes $S =$ {John promoted, Rita promoted, Aslam promoted, Gurpreet promoted}.

You are told that the chances of John’s promotion is the same as that of Gurpreet, Rita’s chances of promotion are twice as likely as John’s, Aslam’s chances are four times that of John.

(a) Determine $P$ (John promoted), $P$ (Rita promoted), $P$ (Aslam promoted), $P$ (Gurpreet promoted)?

Ans:Given:Total number of persons $= 4$

Probability of John’s promotion $=$ Probability of Gurpreet’s promotion

Probability of Rita’s promotion $=$$2 \times$ Probability of John’s promotion

Probability of Aslam’s promotion $=$$4 \times$ Probability of John’s promotion

Assume $P\left( W \right)$, $P\left( X \right)$, $P\left( Y \right)$ and $P\left( Z \right)$ as the probabilities of promotion of the four persons. Form relations between them and use the formula $P\left( W \right) + P\left( X \right) + P\left( Y \right) + P\left( Z \right) = 1$ to find their values.

Assuming $P\left( W \right)$, $P\left( X \right)$, $P\left( Y \right)$ and $P\left( Z \right)$ as the probabilities of promotion of John, Rita, Aslam and Gurpreet respectively. All the events are mutually exclusive that means no two of them can occur simultaneously.

According to the information given,

$P\left( W \right) = P\left( Z \right)$ … (1)

$P\left( X \right) = 2P\left( W \right)$ … (2)

$P\left( Y \right) = 4P\left( W \right)$ … (3)

Using the formula $P\left( W \right) + P\left( X \right) + P\left( Y \right) + P\left( Z \right) = 1$ and solving the three equations,

$P\left( W \right) = \dfrac{1}{8}$, $P\left( X \right) = \dfrac{1}{4}$, $P\left( Y \right) = \dfrac{1}{2}$ and $P\left( Z \right) = \dfrac{1}{8}$

Probability of promotion of John is $P\left( W \right) = \dfrac{1}{8}$.

Probability of promotion of Rita is $P\left( X \right) = \dfrac{1}{4}$.

Probability of promotion of Aslam is $P\left( Y \right) = \dfrac{1}{2}$.

Probability of promotion of Gurpreet is $P\left( Z \right) = \dfrac{1}{8}$.

(b) If $A =$ (John promoted or Gurpreet promoted), find $P\left( A \right)$?

Ans: Given: Total number of persons $= 4$

Probability of John’s promotion $=$ Probability of Gurpreet’s promotion

Probability of Rita’s promotion $=$$2 \times$ Probability of John’s promotion

Probability of Aslam’s promotion $=$$4 \times$ Probability of John’s promotion

According to the information given,

$P\left( W \right) = P\left( Z \right)$ … (1)

$P\left( X \right) = 2P\left( W \right)$ … (2)

$P\left( Y \right) = 4P\left( W \right)$ … (3)

Using the formula $P\left( W \right) + P\left( X \right) + P\left( Y \right) + P\left( Z \right) = 1$ and solving the three equations,

$P\left( W \right) = \dfrac{1}{8}$, $P\left( X \right) = \dfrac{1}{4}$, $P\left( Y \right) = \dfrac{1}{2}$ and $P\left( Z \right) = \dfrac{1}{8}$

Probability of promotion of John or Gurpreet $P\left( A \right) = P\left( {W \cup Z} \right)$.

$\Rightarrow P\left( A \right) = P\left( W \right) + P\left( Z \right) - P\left( {W \cap Z} \right)$

$\Rightarrow P\left( A \right) = \dfrac{1}{8} + \dfrac{1}{8} - 0$

$\Rightarrow P\left( A \right) = \dfrac{1}{4}$

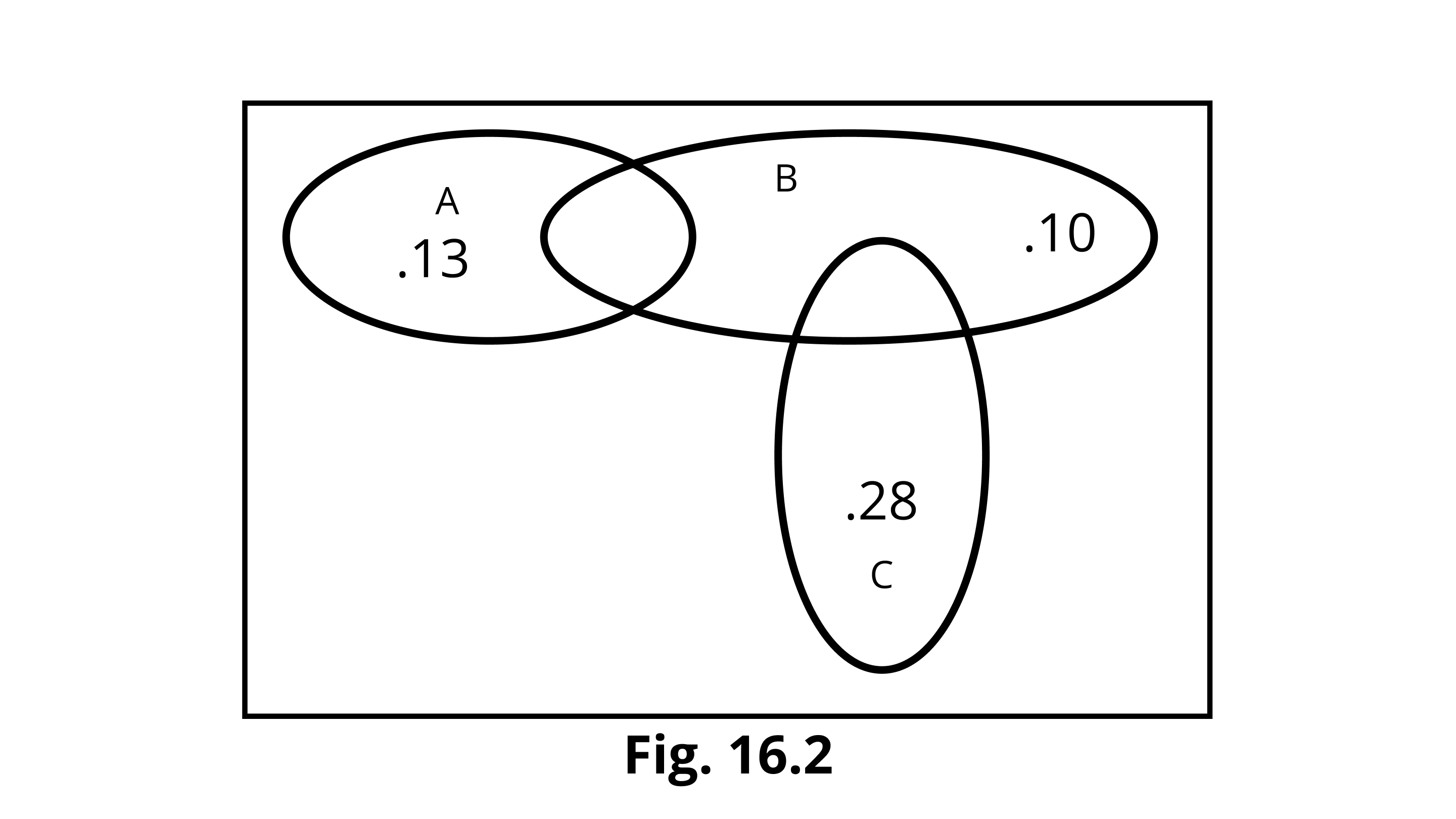
11. The accompanying Venn diagram shows three events $A$, $B$ and $C$, and also the probabilities of the various intersections (for instance $P\left( {A \cap B} \right) = 0.07$). Determine

$\left( a \right)P\left( A \right)$

Ans: Given:

In the Venn diagram: -

$P\left( {{\text{only }}A} \right) = 0.13$

$P\left( {{\text{only }}B} \right) = 0.10$

\[P\left( {{\text{only }}C} \right) = 0.28\]

$P\left( {A \cap B} \right) = 0.07$

$P\left( {B \cap C} \right) = 0.15$

Using the Venn and the formulas of theory solve for each subpart of the question.

Use the formulas: -

$P\left( {B \cap \overline C } \right) = P\left( B \right) - P\left( {B \cap C} \right)$

$P\left( {A \cap \overline B } \right) = P\left( A \right) - P\left( {A \cap B} \right)$

The probability of occurrence of the event $A$ is \[P\left( A \right) = P\left( {{\text{only }}A} \right) + P\left( {A \cap B} \right)\].

$\Rightarrow P\left( A \right) = 0.13 + 0.07$

$\Rightarrow P\left( A \right) = 0.20$

$\left( b \right)P\left( {B \cap \overline C } \right)$

Ans: Given:

In the Venn diagram: -

$P\left( {{\text{only }}A} \right) = 0.13$

$P\left( {{\text{only }}B} \right) = 0.10$

\[P\left( {{\text{only }}C} \right) = 0.28\]

$P\left( {A \cap B} \right) = 0.07$

$P\left( {B \cap C} \right) = 0.15$

Using the Venn and the formulas of theory solve for each subpart of the question.

Use the formulas: -

$P\left( {B \cap \overline C } \right) = P\left( B \right) - P\left( {B \cap C} \right)$

$P\left( {A \cap \overline B } \right) = P\left( A \right) - P\left( {A \cap B} \right)$

Here $\left( {B \cap \overline C } \right)$ states the event of occurrence of $B$ and not $C$.

$\Rightarrow P\left( {B \cap \overline C } \right) = P\left( B \right) - P\left( {B \cap C} \right)$

$\Rightarrow P\left( {B \cap \overline C } \right) = \left( {0.10 + 0.07 + 0.15} \right) - 0.15$

$\Rightarrow P\left( {B \cap \overline C } \right) = 0.17$

$\left( c \right)P\left( {A \cup B} \right)$

Ans: Given:

In the Venn diagram: -

$P\left( {{\text{only }}A} \right) = 0.13$

$P\left( {{\text{only }}B} \right) = 0.10$

\[P\left( {{\text{only }}C} \right) = 0.28\]

$P\left( {A \cap B} \right) = 0.07$

$P\left( {B \cap C} \right) = 0.15$

Using the Venn and the formulas of theory solve for each subpart of the question.

Use the formulas: -

$P\left( {B \cap \overline C } \right) = P\left( B \right) - P\left( {B \cap C} \right)$

$P\left( {A \cap \overline B } \right) = P\left( A \right) - P\left( {A \cap B} \right)$

Here $P\left( {A \cup B} \right)$ is the probability of occurrence of either $A$ or $B$.

$\Rightarrow P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {A \cap B} \right)$

$\Rightarrow P\left( {A \cup B} \right) = \left( {0.13 + 0.07} \right) + \left( {0.10 + 0.07 + 0.15} \right) - 0.07$

$\Rightarrow P\left( {A \cup B} \right) = 0.45$

$\left( d \right)P\left( {A \cap \overline B } \right)$

Ans: Given:

In the Venn diagram: -

$P\left( {{\text{only }}A} \right) = 0.13$

$P\left( {{\text{only }}B} \right) = 0.10$

\[P\left( {{\text{only }}C} \right) = 0.28\]

$P\left( {A \cap B} \right) = 0.07$

$P\left( {B \cap C} \right) = 0.15$

Using the Venn and the formulas of theory solve for each subpart of the question.

Use the formulas: -

$P\left( {B \cap \overline C } \right) = P\left( B \right) - P\left( {B \cap C} \right)$

$P\left( {A \cap \overline B } \right) = P\left( A \right) - P\left( {A \cap B} \right)$

Here $\left( {A \cap \overline B } \right)$ states the event of occurrence of $A$ and not $B$.

$\Rightarrow P\left( {A \cap \overline B } \right) = P\left( A \right) - P\left( {A \cap B} \right)$

$\Rightarrow P\left( {A \cap \overline B } \right) = \left( {0.13 + 0.07} \right) - 0.07$

$\Rightarrow P\left( {A \cap \overline B } \right) = 0.13$

$\left( e \right)P\left( {B \cap C} \right)$

Ans: Given:

In the Venn diagram: -

$P\left( {{\text{only }}A} \right) = 0.13$

$P\left( {{\text{only }}B} \right) = 0.10$

\[P\left( {{\text{only }}C} \right) = 0.28\]

$P\left( {A \cap B} \right) = 0.07$

$P\left( {B \cap C} \right) = 0.15$

Using the Venn and the formulas of theory solve for each subpart of the question.

Use the formulas: -

$P\left( {B \cap \overline C } \right) = P\left( B \right) - P\left( {B \cap C} \right)$

$P\left( {A \cap \overline B } \right) = P\left( A \right) - P\left( {A \cap B} \right)$

Here $\left( {B \cap C} \right)$ states the event of occurrence of both $A$ and $B$.

$\Rightarrow P\left( {B \cap C} \right) = 0.15$

$\left( f \right)$ Probability of exactly one of the three occurs.

Ans: Given:

In the Venn diagram: -

$P\left( {{\text{only }}A} \right) = 0.13$

$P\left( {{\text{only }}B} \right) = 0.10$

\[P\left( {{\text{only }}C} \right) = 0.28\]

$P\left( {A \cap B} \right) = 0.07$

$P\left( {B \cap C} \right) = 0.15$

Using the Venn and the formulas of theory solve for each subpart of the question.

Use the formulas: -

$P\left( {B \cap \overline C } \right) = P\left( B \right) - P\left( {B \cap C} \right)$

$P\left( {A \cap \overline B } \right) = P\left( A \right) - P\left( {A \cap B} \right)$

Probability of exactly one of the three occurs means \[P\left( {{\text{only }}A} \right) + P\left( {{\text{only }}B} \right) + P\left( {{\text{only }}C} \right)\].

$\Rightarrow $ Required probability $= 0.13 + 0.10 + 0.28$

$\Rightarrow $ Required probability $= 0.51$

12. One urn contains two black balls (labelled $B1$ and $B2$) and one white ball. A second urn contains one black ball and two white balls (labelled $W1$ and $W2$). Suppose the following experiment is performed. One of the two urns is chosen at random. Next a ball is randomly chosen from the urn. Then a second ball is chosen at random from the same urn without replacing the first ball.

(a) Write the sample space showing all possible outcomes.

Ans: Given: Two black balls (labelled $B1$ and $B2$) and one white ball in the first urn.

Two white balls (labelled $W1$ and $W2$) and one black ball in the second urn.

One of the two urns is chosen then a ball is chosen and then a second ball is chosen without replacement.

Find all the possible combinations that can be made in selecting the two balls one after the other and not at once. Check the favourable number of sample spaces for the subparts.

Let us represent the single white ball in the first urn as $W$ and the single black ball in the second urn as $B$. The possible combinations of selecting the two balls one after the other from the urns is the total number of sample spaces given as,

\[n\left( S \right) = \left\{ {B1B2,{\text{ }}B2B1,{\text{ }}B1W,{\text{ }}WB1,{\text{ }}B2W,{\text{ }}WB2,{\text{ }}W1W2,{\text{ }}W2W1,{\text{ }}BW1,{\text{ }}W1B,{\text{ }}BW2,{\text{ }}W2B} \right\} = 12\]

(b) What is the probability that two black balls are chosen?

Ans: Given: Two black balls (labelled $B1$ and $B2$) and one white ball in the first urn.

Two white balls (labelled $W1$ and $W2$) and one black ball in the second urn.

One of the two urns is chosen then a ball is chosen and then a second ball is chosen without replacement.

Find all the possible combinations that can be made in selecting the two balls one after the other and not at once. Check the favourable number of sample spaces for the subparts.

The combinations where two blacks balls are chosen is $n\left( X \right) = \left\{ {B1B2,{\text{ }}B2B1} \right\} = 2$.

Therefore, the required probability is $\dfrac{{n\left( X \right)}}{{n\left( S \right)}} = \dfrac{2}{{12}} = \dfrac{1}{6}$.

Ans: Given: Two black balls (labelled $B1$ and $B2$) and one white ball in the first urn.

Two white balls (labelled $W1$ and $W2$) and one black ball in the second urn.

One of the two urns is chosen then a ball is chosen and then a second ball is chosen without replacement.

Find all the possible combinations that can be made in selecting the two balls one after the other and not at once. Check the favourable number of sample spaces for the subparts.

The combinations where two balls of opposite colours are chosen is $n\left( Y \right) = \left\{ {B1W,{\text{ }}WB1,{\text{ }}B2W,{\text{ }}WB2,BW1,{\text{ }}W1B,{\text{ }}BW2,{\text{ }}W2B} \right\} = 8$.

Therefore, the required probability is $\dfrac{{n\left( Y \right)}}{{n\left( S \right)}} = \dfrac{8}{{12}} = \dfrac{2}{3}$.

13. A bag contains $8$ red and $5$ white balls. Three balls are drawn at random. Find the probability that:

(a) All the three balls are white.

Ans: Given: Total number of red balls $= 8$

Total number of white balls $= 5$

Three balls are drawn at random.

Use the formula ${}^{13}{C_3}$ to find the total number of sample spaces.

Select the balls using the formula of combination for each subpart.

Since there are a total of $13$ balls and any $3$ balls can be selected in ${}^{13}{C_3}$ ways, so the total number of sample space is $n\left( S \right) = {}^{13}{C_3}$.

To select all the three white balls they must be selected from the given $5$ white balls, so the number of favourable sample spaces is $n\left( A \right) = {}^5{C_3}$.

Therefore, the required probability is $= \dfrac{{n\left( A \right)}}{{n\left( S \right)}} = \dfrac{{{}^5{C_3}}}{{{}^{13}{C_3}}} = \dfrac{5}{{143}}$.

(b) All the three balls are red.

Ans: Given: Total number of red balls $= 8$

Total number of white balls $= 5$

Three balls are drawn at random.

Use the formula ${}^{13}{C_3}$ to find the total number of sample spaces.

Select the balls using the formula of combination for each subpart.

Since there are a total of $13$ balls and any $3$ balls can be selected in ${}^{13}{C_3}$ ways, so the total number of sample space is $n\left( S \right) = {}^{13}{C_3}$.

To select all the three red balls they must be selected from the given $8$ red balls, so the number of favourable sample spaces is $n\left( B \right) = {}^8{C_3}$.

Therefore, the required probability is $= \dfrac{{n\left( B \right)}}{{n\left( S \right)}} = \dfrac{{{}^8{C_3}}}{{{}^{13}{C_3}}} = \dfrac{{28}}{{143}}$.

Ans: Given: Total number of red balls $= 8$

Total number of white balls $= 5$

Three balls are drawn at random.

Use the formula ${}^{13}{C_3}$ to find the total number of sample spaces.

Select the balls using the formula of combination for each subpart.

Since there are a total of $13$ balls and any $3$ balls can be selected in ${}^{13}{C_3}$ ways, so the total number of sample space is $n\left( S \right) = {}^{13}{C_3}$.

To select one red ball the number of ways is \[{}^8{C_1}\] and to select two white balls the number of ways is \[{}^5{C_2}\]. So the number of favourable sample spaces is $n\left( C \right) = {}^8{C_1} \times {}^5{C_2}$.

Therefore, the required probability is $= \dfrac{{n\left( C \right)}}{{n\left( S \right)}} = \dfrac{{{}^8{C_1} \times {}^5{C_2}}}{{{}^{13}{C_3}}} = \dfrac{{40}}{{143}}$.

14. If the letters of the word ASSASSINATION are arranged at random. Find the probability that

(a) Four S’s come consecutively in the word

Ans: Given:The letters of the word Assassination are arranged.

Find the total number of sample spaces by arranging all the thirteen letters of the word and dividing it by the product of the factorial of the number of times each letter is repeating.

Arrange the letters as per the condition given in the subparts to find the favourable sample spaces.

There are $13$ letters in the word ASSASSINATION in which A is repeated $3$ times, S is repeated $4$ times, I is repeated $2$ times and N is repeated $2$ times. So the number of different words that can be formed is the total number of sample spaces $n\left( S \right) = \dfrac{{13!}}{{4!{\text{ }} \times {\text{ }}3!{\text{ }} \times {\text{ }}2!{\text{ }} \times {\text{ }}2!}}$.

All the four S’s come together so they can be assumed as a single unit. Since, they are identical alphabets, so there is no meaning of arranging them among themselves. The remaining $9$ alphabets and this single unit can be considered as $10$ objects and they can be arranged in $n\left( A \right) = \dfrac{{10!}}{{3!{\text{ }} \times {\text{ }}2!{\text{ }} \times {\text{ }}2!}}$ ways.

Therefore, the required probability is $\dfrac{{n\left( A \right)}}{{n\left( S \right)}} = \dfrac{2}{{143}}$.

(b) Two I’s and two N’s come together

Ans: Given:The letters of the word ASSASSINATION are arranged.

Find the total number of sample spaces by arranging all the thirteen letters of the word and dividing it by the product of the factorial of the number of times each letter is repeating.

Arrange the letters as per the condition given in the subparts to find the favourable sample spaces.

Here two I’s and two N’s come together (IINN). These four letters can be arranged in $\dfrac{{4!}}{{2!{\text{ }} \times {\text{ }}2!}}$ ways among themselves. The remaining $9$ alphabets and this single unit can be considered as $10$ objects and they can be arranged in $\dfrac{{10!}}{{4! \times 3!}}$ ways. So the number of favorable arrangements is $n\left( B \right) = \dfrac{{4!}}{{2!{\text{ }} \times {\text{ }}2!}}{\text{ }} \times {\text{ }}\dfrac{{10!}}{{4!{\text{ }} \times {\text{ }}3!}}$.

Therefore, the required probability is $\dfrac{{n\left( B \right)}}{{n\left( S \right)}} = \dfrac{2}{{143}}$.

Ans: Given:The letters of the word ASSASSINATION are arranged.

Find the total number of sample spaces by arranging all the thirteen letters of the word and dividing it by the product of the factorial of the number of times each letter is repeating.

Arrange the letters as per the condition given in the subparts to find the favourable sample spaces.

Let us assume that all the three A’s come together so they can be assumed as a single unit. They are identical alphabets. The remaining $10$ alphabets and this single unit can be considered as $11$ objects and they can be arranged in $n\left( C \right) = \dfrac{{11!}}{{4!{\text{ }} \times {\text{ }}2!{\text{ }} \times {\text{ }}2!}}$ ways.

Therefore, the probability that all the A’s comes together is $\dfrac{{n\left( C \right)}}{{n\left( S \right)}} = \dfrac{1}{{26}}$.

Hence, the probability that all the A’s does not come together is $\left( {1 - \dfrac{{n\left( C \right)}}{{n\left( S \right)}}} \right) = \dfrac{{25}}{{26}}$.

(d) No two A’s are coming together.

Ans: Given:The letters of the word ASSASSINATION are arranged.

Find the total number of sample spaces by arranging all the thirteen letters of the word and dividing it by the product of the factorial of the number of times each letter is repeating.

Arrange the letters as per the condition given in the subparts to find the favourable sample spaces.

Here no two A’s come together. Let us arrange the remaining letters first.

_ S _ S _ S _ S _ I _ N _ T _ I _ O _ N _

The three A’s can be filled at any $3$ of the $11$ blank spaces in ${}^{11}{C_3}$ ways (arrangement not required as they are identical). The remaining $10$ letters can be arranged in $\dfrac{{10!}}{{4!{\text{ }} \times {\text{ }}2!{\text{ }} \times {\text{ }}2!}}$ ways. So the number of favourable arrangements is $n\left( D \right) = {}^{11}{C_3} \times \dfrac{{10!}}{{4!{\text{ }} \times {\text{ }}2!{\text{ }} \times {\text{ }}2!}}$.

Therefore, the required probability is $\dfrac{{n\left( D \right)}}{{n\left( S \right)}} = \dfrac{{15}}{{26}}$.

15. A card is drawn from a deck of $52$ cards. Find the probability of getting a king or a heart or a red card.

Ans: Given: A deck of $52$ cards and one card is drawn.

Assume $P\left( K \right)$, $P\left( H \right)$ and $P\left( R \right)$ as the probabilities of drawing a king, a heart and a red card respectively.

Use the formula $P\left( {K \cup H \cup R} \right) = P\left( K \right) + P\left( H \right) + P\left( R \right) - P\left( {K \cap H} \right) - P\left( {H \cap R} \right) - P\left( {K \cap R} \right) + P\left( {K \cap H \cap R} \right)$ to solve for the $L.H.S$.

Let us assume $P\left( K \right)$, $P\left( H \right)$ and $P\left( R \right)$ as the probabilities of drawing a king, a heart and a red card respectively. The number of ways to draw a $1$ card from $52$ cards is $n\left( S \right) = {}^{52}{C_1}$.

There are four kings, thirteen hearts cards and 26 red cards.

Now, there is $1$ card which is both king and red, $13$ cards which are both red and hearts, $2$ cards which are both red and king.

There is only one card which is king, hearts and red.

So the probability of drawing a king, a heart or a red card is $P\left( {K \cup H \cup R} \right)$ which is

$= P\left( K \right) + P\left( H \right) + P\left( R \right) - P\left( {K \cap H} \right) - P\left( {H \cap R} \right) - P\left( {K \cap R} \right) + P\left( {K \cap H \cap R} \right)$

$= \dfrac{4}{{52}} + \dfrac{{13}}{{52}} + \dfrac{{26}}{{52}} - \dfrac{1}{{52}} - \dfrac{{13}}{{52}} - \dfrac{2}{{52}} + \dfrac{1}{{52}}$

$= \dfrac{{28}}{{52}}$

$= \dfrac{7}{{13}}$

16. A sample space consists of $9$ elementary outcomes ${e_1}$, ${e_2}$, …, ${e_9}$ whose probabilities are

$P\left( {{e_1}} \right) = P\left( {{e_2}} \right) = 0.08$, $P\left( {{e_3}} \right) = P\left( {{e_4}} \right) = P\left( {{e_5}} \right) = 0.1$

$P\left( {{e_6}} \right) = P\left( {{e_7}} \right) = 0.2$, $P\left( {{e_8}} \right) = P\left( {{e_9}} \right) = 0.07$

Suppose $A = \left\{ {{e_1}, {e_2}, {e_8}} \right\}$ and $B = \left\{ {{e_2}, {e_5}, {e_8}, {e_9}} \right\}$.

(a) Calculate $P\left( A \right)$, $P\left( B \right)$, and $P\left( {A \cap B} \right)$.

Ans: Given: The $9$ elementary outcomes ${e_1}$, ${e_2}$, …, ${e_9}$ and their probabilities.

$A = \left\{ {{e_1},{\text{ }}{e_2},{\text{ }}{e_8}} \right\}$

$B = \left\{ {{e_2},{\text{ }}{e_5},{\text{ }}{e_8},{\text{ }}{e_9}} \right\}$

Use the formulas: -

$P\left( A \right) = P\left( {{e_1}} \right) + P\left( {{e_2}} \right) + P\left( {{e_8}} \right)$ and $P\left( B \right) = P\left( {{e_2}} \right) + P\left( {{e_5}} \right) + P\left( {{e_8}} \right) + P\left( {{e_9}} \right)$

$P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {A \cap B} \right)$

$P\left( {\overline B } \right) = 1 - P\left( B \right)$

Since $A = \left\{ {{e_1},{\text{ }}{e_2},{\text{ }}{e_8}} \right\}$, therefore,

$\Rightarrow P\left( A \right) = P\left( {{e_1}} \right) + P\left( {{e_2}} \right) + P\left( {{e_8}} \right)$

$\Rightarrow P\left( A \right) = 0.08 + 0.08 + 0.07$

$\Rightarrow P\left( A \right) = 0.23$

Since $B = \left\{ {{e_2},{\text{ }}{e_5},{\text{ }}{e_8},{\text{ }}{e_9}} \right\}$, therefore,

$\Rightarrow P\left( B \right) = P\left( {{e_2}} \right) + P\left( {{e_5}} \right) + P\left( {{e_8}} \right) + P\left( {{e_9}} \right)$

$\Rightarrow P\left( B \right) = 0.08 + 0.1 + 0.07 + 0.07$

$\Rightarrow P\left( B \right) = 0.32$

Now, $\left( {A \cap B} \right)$ is the set of common elementary outcomes of $A$ and $B$. So $\left( {A \cap B} \right) = \left\{ {{e_5},{\text{ }}{e_8}} \right\}$, therefore,

$\Rightarrow P\left( {A \cap B} \right) = P\left( {{e_5}} \right) + P\left( {{e_8}} \right)$

$\Rightarrow P\left( {A \cap B} \right) = 0.1 + 0.07$

$\Rightarrow P\left( {A \cap B} \right) = 0.17$

(b) Using the additional law of probability, calculate $P\left( {A \cup B} \right)$.

Ans: Given: The $9$ elementary outcomes ${e_1}$, ${e_2}$, …, ${e_9}$ and their probabilities.

$A = \left\{ {{e_1},{\text{ }}{e_2},{\text{ }}{e_8}} \right\}$

$B = \left\{ {{e_2},{\text{ }}{e_5},{\text{ }}{e_8},{\text{ }}{e_9}} \right\}$

Use the formulas: -

$P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {A \cap B} \right)$

$P\left( {\overline B } \right) = 1 - P\left( B \right)$

According to the addition law of probability $P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {A \cap B} \right)$,

$\Rightarrow P\left( {A \cup B} \right) = 0.23 + 0.25 - 0.17$

$\Rightarrow P\left( {A \cup B} \right) = 0.23 + 0.32 - 0.40$

(c) List the composition of the event $A’E B$, and calculate $P\left( {A \cup B} \right)$ by adding the probabilities of the elementary outcomes.

Ans: Given: The $9$ elementary outcomes ${e_1}$, ${e_2}$, …, ${e_9}$ and their probabilities.

$A = \left\{ {{e_1},{\text{ }}{e_2},{\text{ }}{e_8}} \right\}$

$B = \left\{ {{e_2},{\text{ }}{e_5},{\text{ }}{e_8},{\text{ }}{e_9}} \right\}$

Use the formulas: -

$P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {A \cap B} \right)$

$P\left( {\overline B } \right) = 1 - P\left( B \right)$

The event $\left( {A \cup B} \right)$ is the set of all the elements present in either $A$ or $B$. So the composition of $\left( {A \cup B} \right)$ is $\left\{ {{e_1},{\text{ }}{e_2},{\text{ }}{e_5},{\text{ }}{e_8},{\text{ }}{e_9}} \right\}$, therefore,

$\Rightarrow P\left( {A \cup B} \right) = P\left( {{e_1}} \right) + P\left( {{e_2}} \right) + P\left( {{e_5}} \right) + P\left( {{e_8}} \right) + P\left( {{e_9}} \right)$

$\Rightarrow P\left( {A \cup B} \right) = 0.08 + 0.08 + 0.1 + 0.07 + 0.07$

$\Rightarrow P\left( {A \cup B} \right) = 0.40$

(d) Calculate $P\left( {\overline B } \right)$ from $P\left( B \right)$, also calculate $P\left( {\overline B } \right)$ directly from the elementary outcomes of $\overline B $.

Ans: Given: The $9$ elementary outcomes ${e_1}$, ${e_2}$, …, ${e_9}$ and their probabilities.

$A = \left\{ {{e_1},{\text{ }}{e_2},{\text{ }}{e_8}} \right\}$

$B = \left\{ {{e_2},{\text{ }}{e_5},{\text{ }}{e_8},{\text{ }}{e_9}} \right\}$

Use the formulas: -

$P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {A \cap B} \right)$

$P\left( {\overline B } \right) = 1 - P\left( B \right)$

Using $P\left( B \right)$ the value of $P\left( {\overline B } \right)$ is given as $1 - P\left( B \right)$.

$\Rightarrow P\left( {\overline B } \right) = 1 - P\left( B \right)$

$\Rightarrow P\left( {\overline B } \right) = 1 - 0.32$

$\Rightarrow P\left( {\overline B } \right) = 0.68$

Since $B = \left\{ {{e_2},{\text{ }}{e_5},{\text{ }}{e_8},{\text{ }}{e_9}} \right\}$, so $\overline B = \left\{ {{e_1},{\text{ }}{e_3},{\text{ }}{e_4},{\text{ }}{e_6},{\text{ }}{e_7}} \right\}$, therefore,

$\Rightarrow P\left( {\overline B } \right) = P\left( {{e_1}} \right) + P\left( {{e_3}} \right) + P\left( {{e_4}} \right) + P\left( {{e_6}} \right) + P\left( {{e_7}} \right)$

$\Rightarrow P\left( {\overline B } \right) = 0.08 + 0.1 + 0.1 + 0.2 + 0.2$

$\Rightarrow P\left( {\overline B } \right) = 0.68$

17: Determine the probability $p$ for each of the following events.

(a) An odd number appears in a single toss of a fair die.

Ans: write all the sample space and find the favourable events among them.

When the fair die is tossed one time then the sample spaces are $n\left( S \right) = \left\{ {1,{\text{ }}2,{\text{ }}3,{\text{ }}4,{\text{ }}5,{\text{ }}6} \right\} = 6$. There are three odd numbers, so the favourable events are $n\left( A \right) = \left\{ {1,{\text{ }}3,{\text{ }}5} \right\} = 3$.

Therefore, the probability $p$ is $\dfrac{{n\left( A \right)}}{{n\left( S \right)}} = \dfrac{3}{6} = \dfrac{1}{2}$.

(b) At least one head appears in two tosses of a fair coin.

Ans: write all the sample space and find the favourable events among them.

When two fair coins are tossed the sample spaces are $n\left( S \right) = \left\{ {HH,{\text{ }}HT,{\text{ }}TH,{\text{ }}TT} \right\} = 4$.

There are three outcomes where at least one head appears, so $n\left( B \right) = \left\{ {HH,{\text{ }}HT,{\text{ }}TH} \right\} = 3$.

Therefore, the probability $p$ is $\dfrac{{n\left( B \right)}}{{n\left( S \right)}} = \dfrac{3}{4}$.

(c) A king, $9$ of hearts, or $3$ of spades appears in drawing a single card from a well shuffled ordinary deck of $52$ cards.

Ans: consider that there are four kings, one $9$ of hearts and one $3$ of spades in a pack.

In a deck of $52$ cards the number of ways to draw a card is the total number of sample spaces given as $n\left( S \right) = {}^{52}{C_1} = 52$.

There are four kings (one in each suit), one $9$ of hearts and one $3$ of spades in a pack. So the number of favourable outcomes is $n\left( C \right) = \left( {4 + 1 + 1} \right) = 6$.

Therefore, the probability $p$ is $\dfrac{{n\left( C \right)}}{{n\left( S \right)}} = \dfrac{6}{{52}} = \dfrac{3}{{26}}$.

(d) The sum of $6$ appears in a single toss of a pair of fair dice.

Ans: write all the sample space and find the favourable events among them.

When a pair of dice is tossed one time then there are ${6^2} = 36$ combinations of outcomes possible. So the number of sample spaces is $n\left( S \right) = 36$.

The sum of $6$ appears in the cases $\left( {1,5} \right)$, $\left( {5,1} \right)$, $\left( {2,4} \right)$, $\left( {4,2} \right)$ and $\left( {3,3} \right)$, so the number of favourable outcomes is $n\left( D \right) = 5$.

Therefore, the probability $p$ is $\dfrac{{n\left( D \right)}}{{n\left( S \right)}} = \dfrac{5}{{36}}$.

Objective Type Questions:

18: In a non-leap year, the probability of having \[53\] Tuesday or \[53\] Wednesday is

(A) \[\dfrac{1}{7}\]

(B) \[\dfrac{2}{7}\]

(D) None of these. \[\]

Ans: Given: Non-leap year, There are \[365\] days that have \[52\] weeks and \[1\] days.

$P\left( A \right){\text{ }} = \dfrac{{\left\{ {{\text{Tuesday}}} \right\}}}{{\left\{ {S{\text{unday, Monday, Tuesday, Wednesday, Thursday, Friday, Saturday}}} \right\}}}$

$P\left( B \right){\text{ }} = \dfrac{{\left\{ {{\text{Wednesday}}} \right\}}}{{\left\{ {{\text{Sunday, Monday, Tuesday, Wednesday, Thursday, Friday, Saturday}}} \right\}}}$

If this day is a Tuesday or Wednesday then, the year will have\[53\]Tuesday

Or \[53\] Wednesday.

\[\therefore \] Required Probability \[ = \dfrac{1}{7} + \dfrac{1}{7} = \dfrac{2}{7}\]

Correct Answer: B

19. Three numbers are chosen from \[1{\text{ }}\] to \[20\]. Find the probability that they are not consecutive

(A) \[\dfrac{{186}}{{190}}\]

(B) \[\dfrac{{187}}{{190}}\]

(D) \[\dfrac{{18}}{{^{20}{C_3}}}\]

Ans: Given: Three numbers are chosen from \[1{\text{ }}\] to \[20\]

The probability that the numbers are not a consecutive \[ = 1- \] probability of the numbers being consecutive.

Since the set of consecutive numbers are from$1{ - }20$

${\text{P}}\left( {1,{\text{ }}2,{\text{ }}3} \right),{\text{ }}\left( {2,{\text{ }}3{\text{ }},4} \right){\text{ }},\left( {3,{\text{ }}4,{\text{ }}5} \right){\text{ }}........({\text{ }}18,{\text{ }}19,{\text{ }}20){\text{i}}{\text{.e}}.,{\text{ }}18.$

${\text{P }}\left( {{\text{ consecutive numbers }}} \right){\text{ = }}\dfrac{{18}}{{^{20}{C_3}}}$

$= {\text{ }}\dfrac{{18}}{{\dfrac{{20{ } \times{ }19{ } \times{ }18}}{{3{ }!}}}}{\text{ }} = {\text{ }}\dfrac{3}{{19}}$

${\text{P }}\left( {{\text{ three number are not consecutive}}} \right){\text{ }} = {\text{ }}1{\text{ }} - {\text{ }}\dfrac{3}{{190}}{\text{ }} = {\text{ }}\dfrac{{187}}{{190}}$

Correct Answer: B

20. While shuffling a pack of \[52\] Playing cards and \[2\] got accidentally dropped. Find the probability that the missing cards to be of different colours is

(A) \[\dfrac{{29}}{{52}}\]

(B) \[\dfrac{1}{2}\]

(D) \[\dfrac{{27}}{{51}}\]

Ans: Given: While shuffling a pack, \[52\] Playing cards and \[2\] got accidentally dropped.

\[{\text{P}}\left( {{\text{both cards of opposite colour}}} \right) = \dfrac{{^{26}{C_1}\times {{ }^{26}}{C_1}}}{{^{52}{C_2}}}\]

On the back of \[52\] cards,\[26\] red colour and \[26\] black colour.

\[{\text{P}}\left( {{\text{both cards of opposite colour}}} \right) = \dfrac{{^{26}{C_1}\times {{ }^{26}}{C_1}}}{{^{52}{C_2}}} = \dfrac{{26 \times 26}}{{\dfrac{{52 \times 51}}{2}}} = \dfrac{{26}}{{51}}\]

Correct answer: C

21. Seven persons are to be seated in a row. The probability that two particular persons sit next to each other

(A) $\dfrac{1}{3}$

(B) $\dfrac{1}{6}$

(D) $\dfrac{1}{2}$

Ans: Given: Seven persons are to be seated in a row

With the help of the basic formulas,

\[n! = n \times (n - 1)!\]

${\text{Required probability = }}\dfrac{{{\text{Number of arrangement}}}}{{{\text{Total number of arrangement of 7 persons}}}}$

If two particular persons sit next to each other, then consider two people a group.

Now we have to arrange \[6\] persons.

Number of arrangements \[ = 2! \times 6!\]

Total number of arrangement of \[7\] persons \[ = 7!\]

Required probability \[ = \dfrac{{2! \times 6!}}{{7!}}\]\[ = \dfrac{2}{7}\]

Correct Answer: C

22. Without repetition of the numbers, four-digit numbers are formed with the numbers \[0, 2, 3, 5.\] the probability of such a number divisible by \[5\] is

(A) $\dfrac{1}{5}$

(B) $\dfrac{4}{5}$

(D) $\dfrac{5}{9}$

Ans: Given: four-digit numbers are formed with the numbers \[0,{\text{ }}2,{\text{ }}3,{\text{ }}5.\]

With the help of the formulas,

\[n! = n \times (n - 1)!\]

Required probability \[ = \dfrac{{{\text{total number of numbers divisible by }}5{\text{ }}}}{{{\text{total number of numbers formed from }}0,2,3,5}}\]

Number divisible by 5 has unit place digit $\rightarrow$ '0' or '5'

If a unit place is '0', the first three places can be filled in $3 !$ ways.

If a unit place is '5', then the first place can be filled in two ways.

The second and third places can be filled in 2! ways.

So number ending with the digit '5' $=2 \times 2 !=4$

Total numbers formed from $0,2,3,5$ are divisible by $5=3!+4=10=n(E)$

Required probability $=\dfrac{10}{18}=\dfrac{5}{9}$

Correct Answer: D

23. If A and B is mutually exclusive events, then

(A) \[P\left( A \right) \leqslant P\left( {\overline B } \right)\]

(B) \[P\left( A \right) \geqslant P\left( {\overline B } \right)\]

(D) None of these

Ans: For mutually exclusive events,

$P\left( {A \cap B} \right) = 0$

$P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {A \cap B} \right)$

$P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right)$

$P\left( A \right) + P\left( B \right) \leqslant 1$

$P\left( A \right) \leqslant 1 - P\left( B \right)$

$P\left( A \right) \leqslant P\left( {\overline B } \right)$

Correct Answer: A

Question 24: If \[P{\text{ }}(A \cup B){\text{ }} = {\text{ }}P{\text{ }}(A \cap B)\]. For any two events A and B, then

\[(A)P\left( A \right) = P(B)\]

\[(B)P\left( A \right) > P\left( B \right)\]

\[(C)P\left( A \right) < P\left( B \right)\]

(D)None of these.

Ans: We have,

$P{\text{ }}(A \cup B){\text{ }} = {\text{ }}P{\text{ }}(A \cap B)$

$P\left( A \right) + P(B) - P{\text{ }}(A \cap B) = P{\text{ }}(A \cap B)$

$\left[ {P\left( A \right) - P{\text{ }}(A \cap B)} \right] + \left[ {P(B) - P{\text{ }}(A \cap B)} \right] = 0$

$\left[ {P\left( A \right) - P{\text{ }}(A \cap B)} \right] \geqslant 0$

$\left[ {P\left( B \right) - P{\text{ }}(A \cap B)} \right] \geqslant 0$

$\left[ {P\left( A \right) - P{\text{ }}(A \cap B)} \right] = 0$

Correct answer: A

25. \[6\] boys and \[6\] girls sit in a row at random. The probability that all the girls sit together is

(A)$\dfrac{1}{{432}}$

(B) $\dfrac{{12}}{{431}}$

(D) None of these

Ans: All girls sit together in a group.

Number of arrangements $6 + 1 = 7$ And girls interchange their seats in \[6!\] Ways

Probability \[ = \dfrac{{6! \times 7!}}{{12!}} = \dfrac{1}{{132}}\]

Correct Answer: C

26. A single letter is selected at random from the word ‘PROBABILITY’ the probability that it is a vowel is

(A) \[\dfrac{1}{3}\]

(B) \[\dfrac{4}{{11}}\]

(C)\[\dfrac{2}{{11}}\]

(D) \[\dfrac{3}{{11}}\]

Ans: Total number of alphabets in the word $= 11$

Vowels \[ = 4({\text{O,}}{\text{A,}}{\text{I,}}{\text{I}})\]

\[{\text{P}}\left( {{\text{letter is vowel}}} \right) = \dfrac{4}{{11}}\]

Correct Answer: B

27. If the probabilities for A to fail in an examination are \[0.2\] and that for B is\[0.3\], then the probability that either A or B fails is

(A) \[ > .5\]

(B) \[.5\]

(D) 0

Ans:

${\text{P}}{\text{(A fail)}} = 0.2$

$ {\text{P}}{\text{(B fail)}} = 0.3$

$ {\text{P}}{\text{(Either A Or B fail)}} \leqslant {\text{P}}{\text{(A fail)}}+ {\text{P}}{\text{(B fail)}}$

$\leqslant 0.2+ 0.3$

$\leqslant 0.5$

Correct Answer: C

28. The probability that at least one of the events A and B occur is \[0.6.\] If A and B occur simultaneously with probability \[0.2\], then \[P \left( { A } \right) + P \left( { B} \right)\] is

(A) \[0.4\]

(B) \[0.8\]

(D) \[1.6\]

Ans:

$P\left( {A \cup B} \right) = 0.6$

$P\left( {A \cap B} \right)= 0.2$

$P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {A \cap B} \right)$

$0.6 = P\left( A \right) + P\left( B \right) - 0.2$

$P\left( A \right) + P\left( B \right) = 0.8$

$P\left( {\overline A } \right) + P\left( {\overline B } \right) = 1 - P\left( A \right) + 1 - P\left( B \right) = 2 - \left[ {P\left( A \right) + P\left( B \right)} \right]$

$= 2 - 0.8 = 1.2$

Correct Answer: C

29. If M and N are any two events, the probability that at least one of them occurs is

(A) \[P \left( M \right) + P \left( N \right) - 2P \left( {M\cap N} \right)\]

(B) \[P \left( M \right) + P \left( N \right) - P \left( {M \cap N} \right)\]

(D) \[P \left( M \right) + P \left( N \right) + 2P \left( {M \cap N} \right)\]

Ans: If M and N are any two events.

$\therefore P\left( {M \cup N} \right) = P\left( M \right) + P\left( N \right)- P\left( {M \cap N} \right)$

Correct Answer: B

State Whether the Statements are True or False

30. The probability that a person visiting a zoo will see the giraffe is \[0.72\], the probability that he will see the bears are \[0.84\] and the probability that he will see both is \[0.52.\]

Ans: Let Giraffe$= G$

Bear $ = {\text{B}}$

${\text{P}}\left( {\text{G}} \right) = 0.72$

${\text{P}}\left( {\text{B}} \right) = 0.84$

${\text{P}}\left( G \cup B\right) = 0.52$

${\text{P}}({\text{G}} \cup {\text{B}}) = {\text{P}}\left( {\text{G}} \right) + {\text{P}}\left( {\text{B}} \right) - {\text{P}}\left( {{\text{G}} \cap {\text{B}}} \right)$

\[{\text{P}}(G \cap B) = 0.72 + 0.84 - 0.52 = 1.04\] (This is not possible).

Correct Answer: False

31. The probability that a student will pass his examination is \[0.73,\] the probability of the student getting a compartment is \[0.13\], and the probability that the student will either pass or get compartment is \[0.96.\]

Ans: Given: Student will pass his examination\[ = 0.73\]

Student getting a compartment \[ = 0.13\]

Student will either pass or get compartment \[0.96.\]

The probability,

$P(A) = 0.73,$

$P(B) = 0.13$

\[P(AUB) = 0.96\]

Find \[P(A \cap B)\]

By General addition rule,

\[P(A \cup B) = P(A) + P(B) - P(A \cap B)\]

Substitute the values to general addition rule,

\[ \Rightarrow {\text{P}}({\text{A}} \cup {\text{B}}) = 0.73 + 0.13 - 0\]

\[\therefore A\] and \[B\] are independent events

\[ \Rightarrow {\text{P}}({\text{A}} \cup {\text{B}}) = 0.86\]

But \[P(A \cup B) = 0.96\]

Hence, the given statement is false.

32. The probabilities that a typist will make \[0, 1, 2, 3, 4, 5\] or more mistakes in typing a report are, respectively \[, 0.12, 0.25, 0.36, 0.14, 0.08, 0.11.\]

Ans: Given: Probabilities that a typist will make \[0,{\text{ }}1,{\text{ }}2,{\text{ }}3,{\text{ }}4,{\text{ }}5\]

Mistakes in typing a report are\[,{\text{ }}0.12,{\text{ }}0.25,{\text{ }}0.36,{\text{ }}0.14,{\text{ }}0.08,{\text{ }}0.11.\]

Sum of all probabilities \[ = 1\]

$\therefore P(0) + P(1) + P(2) + P(3) + P(4) + P(5) = 0.12 + 0.25 + 0.36 + 0.14 + 0.08 + 0.11$

\[ = 1.06 > 1\]

Hence, the given statement is False.

33. If \[A\] and \[B\] are two candidates seeking admission in an engineering College. The probability that \[A\] is selected is \[0.5\] and the probability that both A and B are selected is at most .\[3\]. Is it possible that the probability of \[B\] getting selected is \[0.7?\]

Ans: Given: \[{\text{P}}({\text{A}}) = 0.5\] and

\[P(A \cap B) \leqslant 0.3\]

The probability,

\[{\text{P}}({\text{A}}) = 0.5\]

\[P(A \cap B) \leqslant 0.3\]

\[P(A) \times P(B) \leqslant 0.3\]

Substitute,

\[ \Rightarrow 0.5 \times P(B) \leqslant 0.3\]

\[ \Rightarrow P(B) \leqslant \dfrac{{0.3}}{{0.5}}\]

\[ \Rightarrow P(B) \leqslant 0.6\]

Hence the given statement is False.

34. The probability of intersection of two events \[A\] and \[B\] is always less than or equal to those favourable to the event \[A\].

Ans: Given:The probability of intersection of two events\[A\] and \[B\]

\[A\] and \[B\] are two events,

Here,

\[A \cap B \subset A\]

\[ \Rightarrow P(A \cap B) \leqslant P(A)\]

This is always true.

Hence, the given statement is true.

35. The probability of an occurrence of event \[A\] is \[.7\] and that of the occurrence of event \[B\] is \[.3\] and the probability of occurrence of both is \[.4.\]

Ans: Given: \[P(A)\]\[ = .7\]

\[P(B) = .3\]

The probability of an occurrence of both \[ = .4\]

The probability,

${\text{P}}({\text{A}}) = 0.7$

${\text{P}}({\text{B}}) = 0.3$

\[\therefore P(A \cap B) = P(A) \times P(B)\]

Substitute the values of\[P(A)\] and \[P(B)\],

$P(A \cap B) = 0.7 \times 0.3$

$= 0.21$

But the given probability is \[0.4\].

Hence, the given statement is False.

36. The sum of probabilities of two students getting distinction in their final examinations is \[1.2.\]

Ans: Given: Distinction in their final examinations \[ = 1.2.\]

The probability of each student getting distinction in their final examination is less than or equal to \[1\]

Since, the two given events are not related to the given sample space.

Therefore,

The sum of the probabilities of two may be \[1.2\].

Hence, the given statement is true.

37. The probability that the home team will win an upcoming football game is \[0.77\], the probability that it will tie the game is \[0.08\], and the probability that it will lose the game is _____.

Ans: Given:

$P(A) = 0.77$

$P(B) = 0.08$

The probability that it will tie the game \[ = 0.08\],

\[A\] be the event that home team will win the football game

\[B\] be the event that home team will tie the game and,

\[C\] be the event that they will lose the game

Then,

$P(A) = 0.77$

$P(B) = 0.08$

Find the\[P\] or \[P(C)\]

Sum of all Probabilities\[ = 1\]

\[\therefore {\text{P}}({\text{A}}) + {\text{P}}({\text{B}}) + {\text{P}}({\text{C}}) = 1\]

Substitute the values,

\[ \Rightarrow 0.77 + 0.08 + {\text{P}}({\text{C}}) = 1\]

\[ \Rightarrow {\text{P}}({\text{C}}) = 1 - (0.77 + 0.08)\]

\[P(C)\]\[ = 0.15\].

The probability that the home team will win an upcoming football game is \[0.77\], the probability that it will tie the game is\[0.08\], and the probability that it will lose the game is \[0.5.\]

38. If \[e_1, e_2, e_3, e_4\] are the four elementary outcomes in a sample space \[P\left( {e_1 } \right) = .1, P\left( {e_2 } \right) = .5, P\left( {e_3 } \right) = .1,\] then the probability of \[e_4\] is ______.

Ans: Given: Four elementary outcomes\[ = e_1,{\text{ }}e_2,{\text{ }}e_3,{\text{ }}e_4\]

$P\left( {e_1{\text{ }}} \right) = .1,{\text{ }}$

$P\left( {e_2{\text{ }}} \right) = .5,{\text{ }}$

$P\left( {e_3{\text{ }}} \right) = .1$

Sum of all probabilities\[ = 1\]

\[\therefore {\text{P}}\left( {{{\text{e}}_1}} \right) + {\text{P}}\left( {{{\text{e}}_2}} \right) + {\text{P}}\left( {{{\text{e}}_3}} \right) + {\text{P}}\left( {{{\text{e}}_4}} \right) = 1\]

Substitute the values,

\[ \Rightarrow 0.1 + 0.5 + 0.1 + {\text{P}}\left( {{{\text{e}}_4}} \right) = 1\]

\[ \Rightarrow {\text{P}}\left( {{{\text{e}}_4}} \right) = 1 - 0.7\]

\[ \Rightarrow {\text{P}}\left( {{{\text{e}}_4}} \right) = 0.3\]

Therefore ,

If \[e_1,{\text{ }}e_2,{\text{ }}e_3,{\text{ }}e_4\] are the four elementary outcomes in a sample space \[P\left( {e_1{\text{ }}} \right) = .1,{\text{ }}P\left( {e_2{\text{ }}} \right) = .5,{\text{ }}P\left( {e_3{\text{ }}} \right) = .1,\]then the probability of \[e_4\] is \[0.3.\]

39. Let \[S = \left\{ {1, 2, 3, 4, 5, 6} \right\}\] and \[E = \left\{ {1, 3, 5} \right\},\]then \[\overline {\text{E}} \] is _________.

Ans: Given: \[S{\text{ }} = {\text{ }}\left\{ {1,{\text{ }}2,{\text{ }}3,{\text{ }}4,{\text{ }}5,{\text{ }}6} \right\}\]

\[E{\text{ }} = {\text{ }}\left\{ {1,{\text{ }}3,{\text{ }}5} \right\},\]

Given that,

\[{\text{S}} = \{ 1,2,3,4,5,6\} \]

\[{\text{E}} = \{ 1,3,5\} \]

\[\overline {\text{E}} = {\text{S}} - {\text{E}}\]

\[ = \{ 1,2,3,4,5,6\} \]\[ - \{ 1,3,5\} \]

\[ = \{ 2,4,6\} \]

Hence, the value of the filler is \[\left\{ {2,4,6} \right\}.\]

Therefore,

Let \[S = \left\{ {1,{\text{ }}2,{\text{ }}3,{\text{ }}4,{\text{ }}5,{\text{ }}6} \right\}\] and \[{\text{E}} = {\text{ }}\left\{ {1,{\text{ }}3,{\text{ }}5} \right\},\]then \[\overline {\text{E}} \] is \[\left\{ {2,4,6} \right\}.\]

40. If \[{\text{A}}\] and \[{\text{B}}\] are two events associated with a random experiment such that \[P(A) = 0.3,P(B) = 0.2\] and \[P(A \cap B) = 0.1,\] then the value of \[P(A \cap \overline B )\] is_______.

Ans: Given:

${\text{P}}({\text{A}}) = 0.3,$

$ {\text{P}}({\text{B}}) = 0.2$

\[{\text{P}}({\text{A}} \cap {\text{B}}) = 0.1,\]

Given that,

${\text{P}}({\text{A}}) = 0.3,$

${\text{P}}({\text{B}}) = 0.2$

\[{\text{P}}({\text{A}} \cap {\text{B}}) = 0.1\]

\[{\text{P}}({\text{A}} \cap \overline{{B}} ) = {\text{P}}({\text{A}}) - {\text{P}}({\text{A}} \cap {\text{B}})\]

Substitute the values,\[P(A)\] and \[P(B)\]

\[{\text{P}}({\text{A}} \cap {\text{B}})\]\[ = 0.3 - 0.1\]

\[ = 0.2\]

Hence, the value of the filler is \[0.2.\]

Therefore the statement is,

If \[{\text{A}}\] and \[{\text{B}}\] are two events associated with a random experiment such that \[P(A) = 0.3,{\text{P}}({\text{B}}) = 0.2\] and \[{\text{P}}({\text{A}} \cap {\text{B}}) = 0.1,\] then the value of \[{\text{P}}({\text{A}} \cap \overline{{B}} )\] is \[0.2\].

41. The probability of happening of an event\[A\] is \[0.5\] and that of \[B\] is \[0.3\]. If \[A\] and \[B\] are mutually exclusive events, then the probability of neither \[A\] nor \[B\] is ________.

Ans: Given: Probability of happening of an event\[A\] is \[0.5\] and that of \[B\] is \[0.3\].

Given that,

\[{\text{P}}({\text{A}}) = 0.5,\]

\[{\text{P}}({\text{B}}) = 0.3\]

and \[{\text{P}}({\text{A}} \cap {\text{B}}) = 0\]

\[\because {\text{A}}\] and \[{\text{B}}\] are mutually exclusive events

\[{\text{P}}(\overline{{A}} \cap \overline{{B}} ) = {\text{P}}(\overline{{{A}} \cup {\text{B}}} )\]

\[ = 1 - P(A \cup B)\]

\[ = 1 - [P(A) + P(B)]\]

Substitute the values,

\[{\text{P}}(\overline {\text{A}} \cap \overline {\text{B}} )\]\[ = 1 - (0.5 + 0.3)\]

= 1 - 0.8

= 0.2

Hence, the value of the filler is \[0.2.\]

The probability of happening of an event \[A\] is \[0.5\] and that of \[B\] is \[0.3\]. If A and B are mutually exclusive events, then the probability of neither A nor B is \[0.2.\]

42.Match the proposed probability under Column \[{C_1}\] with the appropriate written description under column \[{C_2}\].

\[{C_1}\] Probability	\[{C_2}\] Written description
\[\left( a \right) 0.95\]	(i) An incorrect assignment
\[\left( b \right) 0.02\]	(ii) No chance of happening
\[\left( c \right) - 0.3\]	(iii) As much chance of happening as not
\[\left( d \right) 0.5\]	(iv) Very likely to happen
\[\left( e \right) 0\]	(v) Very little chance of happening

Ans: \[0.95 = \] Very likely to happen, so it is close to \[1{\text{ }}.\]

\[0.02 = \] Very little chance of happening as the probability is very low.

\[ - 0.3 = \] an incorrect assignment because probability is never negative.

\[0.5 = \] as much chance of happening as not because sum of chances of happening and not happening is one.

\[0 = \] no chance of happening.

Hence,

(a)$\leftrightarrow (iv),$

(b) $\leftrightarrow (v),$

(d) $\leftrightarrow (iii),$

(e) $\leftrightarrow (ii)$

43.Match the following

(a) If \[{E_1}\] and \[{E_2}\] are the two mutually exclusive events	(i) \[{E_1}\cap {E_2} = {E_1}\]
(b) If \[{E_1}\] and \[{E_2}\] are the mutually exclusive and exhaustive events	(ii) \[\left( {{E_1} - {E_2} } \right)\cup \left( {{E_1} \cup {E_2}} \right) = {E_1}\]
(c) If \[{E_1}\] and \[{E_2}\] have common outcomes, then	(iii) \[{E_1} \cap {E_2} = \varphi , {E_1}\cup {E_2} = S\]
(d) If \[{E_1}\] and \[{E_2}\] are two events such that \[{E_1} \subset {E_2}\]	(iv) \[{E_1} \cap {E_2} = \varphi \]

Ans: (a) If \[{{\text{E}}_1}\] and \[{{\text{E}}_2}\] are mutually exclusive events, then \[{{\text{E}}_1} \cap {{\text{E}}_2} = \phi .\]

(b) If \[{{\text{E}}_1}\] and \[{{\text{E}}_2}\] are mutually exclusive and exhaustive events then \[{{\text{E}}_1} \cap {{\text{E}}_2} = \phi \] and \[{{\text{E}}_1} \cup {{\text{E}}_2} = {\text{S}}\]

(c) If \[{{\text{E}}_1}\] and \[{{\text{E}}_2}\] have common outcomes, then \[\left( {{E_1} - {E_2}} \right) \cup \left( {{E_1} \cap {E_2}} \right) = {E_1}\]

(d) If \[{E_1}\] and \[{E_2}\] are two events such that \[{{\text{E}}_1} \subset {{\text{E}}_2} \Rightarrow {{\text{E}}_1} \cap {{\text{E}}_2} = {{\text{E}}_1}\]

Hence,

\[{\text{}}(a) \leftrightarrow (iv),(b) \leftrightarrow (iii),(c) \leftrightarrow (ii),(d) \leftrightarrow (i)\] .

The Important Topics For Chapter 16 Probability Class 11 Maths

The important topics are described as the following:

Random experiment
Outcome
Sample Space
Event
Types of events
Impossible and Sure Events
Simple or Elementary Event
Compound Event
Mutually exclusive event
Exhaustive events
An axiomatic approach to probability
Probabilities of equally likely outcomes
Addition rule of probability
Addition rule for a mutually exclusive event

FAQs on NCERT Exemplar for Class 11 Maths Chapter 16 - Probability (Book Solutions)

1. Can the solutions of NCERT Exemplar Class 11 Maths Chapter 16 Solutions be downloaded from Vedantu?

Yes, the solutions can be downloaded from Vedantu’s website for the NCERT Exemplar Class 11 Maths Solutions Chapter 16 in a PDF format. The download will help the students to access the study material with ease and comfort. This will also help them revise the concepts thoroughly and carefully while retaining all they have learned through more practice. The students can look for the desired material on the website and download the same for free of cost. This will further make the students learn the broader concepts of the subject in a structured way.

2. Can the NCERT Exemplar Class 11 Maths Chapter 16 Solutions be referred for CBSE final exam?

Yes, the students of class 11 Maths can refer to the NCERT exemplar solutions chapter 16 for preparing for the CBSE final exams. This will promote them to understand the in-depth fundamentals of the particular concept that they have learned through various other sources for their better performance. The NCERT Exemplar for Class 11 Maths contains questions of high-level thinking ability and hence, promotes the students to use the application-based thinking ability and answer the same. This way the students can also get help in preparing for the competitive exams.

3. What is the NCERT exemplar for class 11 Maths useful for?

The NCERT Exemplars for class 11 Maths are the practice books that include extra questions of a higher level for developing in-depth learning amongst the students. The NCERT Exemplar for Maths is used especially for JEE mains and JEE advanced exams preparation. This is helpful as the CBSE board exams sometimes contain in-depth sums for the mathematics question paper and thus, need the students to apply logic. Thus, the NCERT Exemplar will aid the students in answering the complex mathematical questions that will appear in the final exam.

4. Does the Vedantu NCERT exemplar have solutions?

Yes, Vedantu provides the students with the solutions for all the study material of the NCERT textbooks, references, and question papers to help them prepare well for the exam. While the students are preparing for such an important exam of their life there is a lot of stress that they might be facing and to reduce that, they are being provided with the solutions to clear all the doubts that they may have while preparing for the exam of class 11 Mathematics.

5. Is the NCERT exemplar maths enough additional material for Class 11?

Yes, the NCERT Exemplar of Class 11th and 12th Maths are useful for the exam preparation however, their level suits more to the aspirants of JEE Mains. But, the NCERT Exemplar is enough to get good marks in board exams, as for the JEE Mains studying Exemplar is not at all sufficient alone as the students have to speculate through a number of reference books which contain questions from the previous year and different levels of difficulty, etc. So, studying the NCERT Exemplar will help you fetch good marks in the exams.