NCERT Exemplar for Class 11 Maths Chapter 1 - Sets (Book Solutions)

Solved Examples

Short Answer Type

1. Write the following sets in roster form.

(i) $A=\left\{x \mid x\right.$ is a positive integer less than 10 and $2^{x}-1$ is an odd number $\}$

Given: Sets in set-builder form.

To find: Sets in roster form.

Ans: $2^{x}-1$ is always an odd positive integer for $x$ as a positive integer. Therefore, the set in roster form is,

$A=\{1,2,3,4,5,6,7,8,9\}$

(ii) $\quad C=\left\{x: x^{2}+7 x-8=0, x \in R\right\}.$

Given: Sets in set-builder form.

To find: Sets in roster form.

Ans: Here, by using factorization method

$x^{2}+7 x-8=0$

$\Rightarrow x^{2}+8x-x-8=0$

$\Rightarrow x(x+8)-1(x+8)=0$

$\Rightarrow (x+8)(x-1)=0$

$\Rightarrow x=-8,1$

$\therefore C=\{-8,1\}$

2. State which of the following statements are true and which are false. Justify your answer.

(i) $37 \notin\{x \mid x$ has exactly two positive factors $\}$

Given: Statements in set-builder form.

To find: True or false. 

Ans: There are exactly two factors 1 and 37 . But 37 belongs to a given set Therefore, the statement is false.

(ii) $28 \in \{y \mid$ the sum of all positive factor of $y$ is $2 y\}$

Given: Statements in set-builder form.

To find: True or false.

Ans: The positive factors of 28 are 1, 2, 4, 7, 14, 28 . The sum of positive factors $1+2+4+7+14+28=56$ or $2(28)$ Therefore, the statement is true.

(iii) $\quad 7,747 \in \{\mathrm{t} \mid \mathrm{t}$ is a multiple of 37$\}$

Given: Statements in set-builder form.

To find: True or false.

Ans: The statement is false. Since, 7,747 is not multiple of $37 .$

3. If $X$ and $Y$ are subsets of the universal set $U$, then show that

(i) $\mathrm{Y} \subset \mathrm{XUY}$

Given: $\mathrm{X}$ and $\mathrm{Y}$ are subsets of the universal set $\mathrm{U}$.

To find: Show that  $\mathrm{Y} \subset \mathrm{X} \cup \mathrm{Y}$

Ans: Here,

$X \cup Y=\{x \mid x \in X \text { or } x \in Y\}$

$\Rightarrow x \in Y$

$\Rightarrow x \in X \cup Y$

$\text { Hence, } Y \subset X \cup Y$ .

(ii) $\mathrm{X} \cap \mathrm{Y} \subset \mathrm{X}$

Given: $\mathrm{X}$ and $\mathrm{Y}$ are subsets of the universal set U.

To find: Show that  $\mathrm{X} \cap \mathrm{Y} \subset \mathrm{X}$

Ans: Here,

$X \cap Y=\{x \mid x \in X \text { and } x \in Y\}$

$\Rightarrow \mathrm{x} \in \mathrm{X} \cap \mathrm{Y}$

$\Rightarrow x \in X$

Hence, $X \cap Y \subset X$.

(iii) $\quad X \subset Y \Rightarrow X \cap Y=X$

Given: $X$ and $Y$ are subsets of the universal set U.

To find: Show that  $\quad X \subset Y \Rightarrow X \cap Y=X$

Ans: Here,

$\text { As, } x \in X \cap Y$

$\Rightarrow X \in X$

$\text { Also, } X \cap Y \subset X$

$\text { since, } X \subset Y$

$\Rightarrow X \in X \text { and } x \in Y$

$\Rightarrow X \in X \cap Y$

$\therefore X \subset X \cap Y$

$\text { Hence, } X \subset Y \Rightarrow X \cap Y=X .$

4. Given that $N=\{1,2,3, \ldots \ldots 100\}$, then

(i) Write the subset $A$ of $N$, whose elements are odd numbers.

Given: $\mathrm{N}=\{1,2,3, \ldots \ldots 100\}$.

To find: Subsets of $\mathrm{N}$, for given conditions.

Ans: $ \mathrm{A}=\{1,3,5,7 \ldots .99\}$.

(ii) Write the subset $B$ of $N$, whose elements are represented by $x+2$, where $x \in N$. 

Given: $\mathrm{N}=\{1,2,3, \ldots \ldots 100\}$. To find: Subsets of $\mathrm{N}$, for given conditions.

Ans: Here,

$y=x+2,$

$\text { for } x=1, y=3$

$x=2, y=4 \text { and so on. }$

$\therefore B=\{3,4,5,6 \ldots \ldots 100\} $.

5. Give that $E=\{2,4,6,8,10\}$. If $n$ represents any number of $E$, then, write the following sets containing all numbers represented by

Given: $\mathrm{E}=\{2,4,6,8,10\}$ and $\mathrm{n}$ represent its elements.

To find: Sets containing all numbers represented by,

(i) $\mathrm{n}+1$

Ans: Here,

$A=\{x \mid x=n+1, n \in E\}$

$\text { for } n=2, x=3$

$n=4, x=5$

$\therefore A=\{3,5,7,9,11\}$

(ii) $\mathrm{n}^{2}$

Given: $\mathrm{E}=\{2,4,6,8,10\}$ and $\mathrm{n}$ represent its elements.

To find: Sets containing all numbers represented by, $\mathrm{n}^{2}$

 Ans: Here,

$B=\left\{x \mid x=n^{2}, n \in E\right\}$

$\text { for } n=2, x=4,$

$n=4, x=16 \text { and so on. }$

$B=\{4,16,36,64,100\}$.

6. Let $X=\{1,2,3,4,5,6\}$. If $n$ represents any member of $X$, express the following as sets. 

Given: $X=\{1,2,3,4,5,6\}$ and $n$ represent its elements.

To find: Express sets as,

(i) $\quad \mathrm{n} \in \mathrm{X}$ but $2 \mathrm{n} \notin X$

Ans:  Here,

$A=\{x \mid x \in X \text { and } 2 x \notin X\}$

$4 \in A \text { and } 2 \times 4=8 \notin X,$

$5 \in A \text { and } 2 \times 5=10 \notin X,$

$6 \in A \text { and } 2 \times 6=12 \notin X .$

$\therefore A=\{4,5,6\}$.

(ii) $\mathrm{n}+5=8$

Given: $X=\{1,2,3,4,5,6\}$ and $n$ represent its elements.

To find: Express sets as,

$\mathrm{n}+5=8$

Ans: Here,

$B=\{x \mid x \in X \text { and } x+5=8\}$

$\Rightarrow x=3$

$\therefore B=\{3\}$.

(iii) n is greater than $4.$

Given: $X=\{1,2,3,4,5,6\}$ and n represent its elements.

To find: Express sets as  $\mathrm{n}$ are greater than 4 .

Ans: Here,

$C=\{x \mid x \in X, x>4\}$

$\text { Cleary, } C=\{5,6\}$.

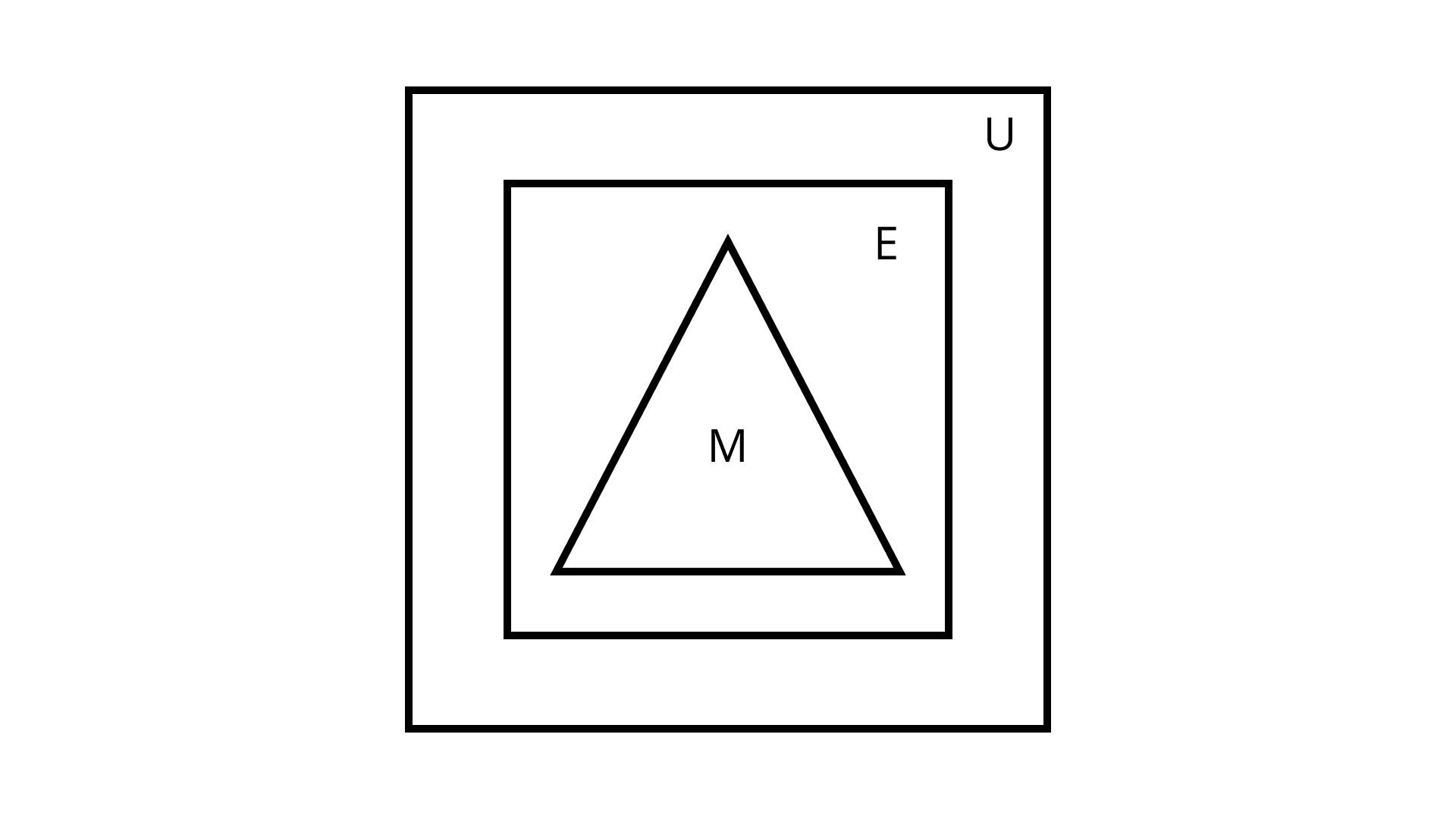
7. Draw the Venn diagrams to illustrate the following relationship among sets $\mathbf{E}, \mathbf{M}$ and $\mathbf{U}_{1}$, where $\mathbf{E}$ is the set of students studying English in a school, $M$ is the set of students studying Mathematics in the same school, $U$ is the set of all students in that school.

(i) All the students who study Mathematics study English, but some students who study English do not study Mathematics.

Given: $\mathrm{E}, \mathrm{M}$ and $\mathrm{U}$ are sets.

To find: Relation between $\mathrm{E}, \mathrm{M}$ and $\mathrm{U}$ using Venn diagram.

Ans: Here, $\mathrm{M} \subset \mathrm{E} \subset \mathrm{U}$.

Therefore, Venn diagram is 

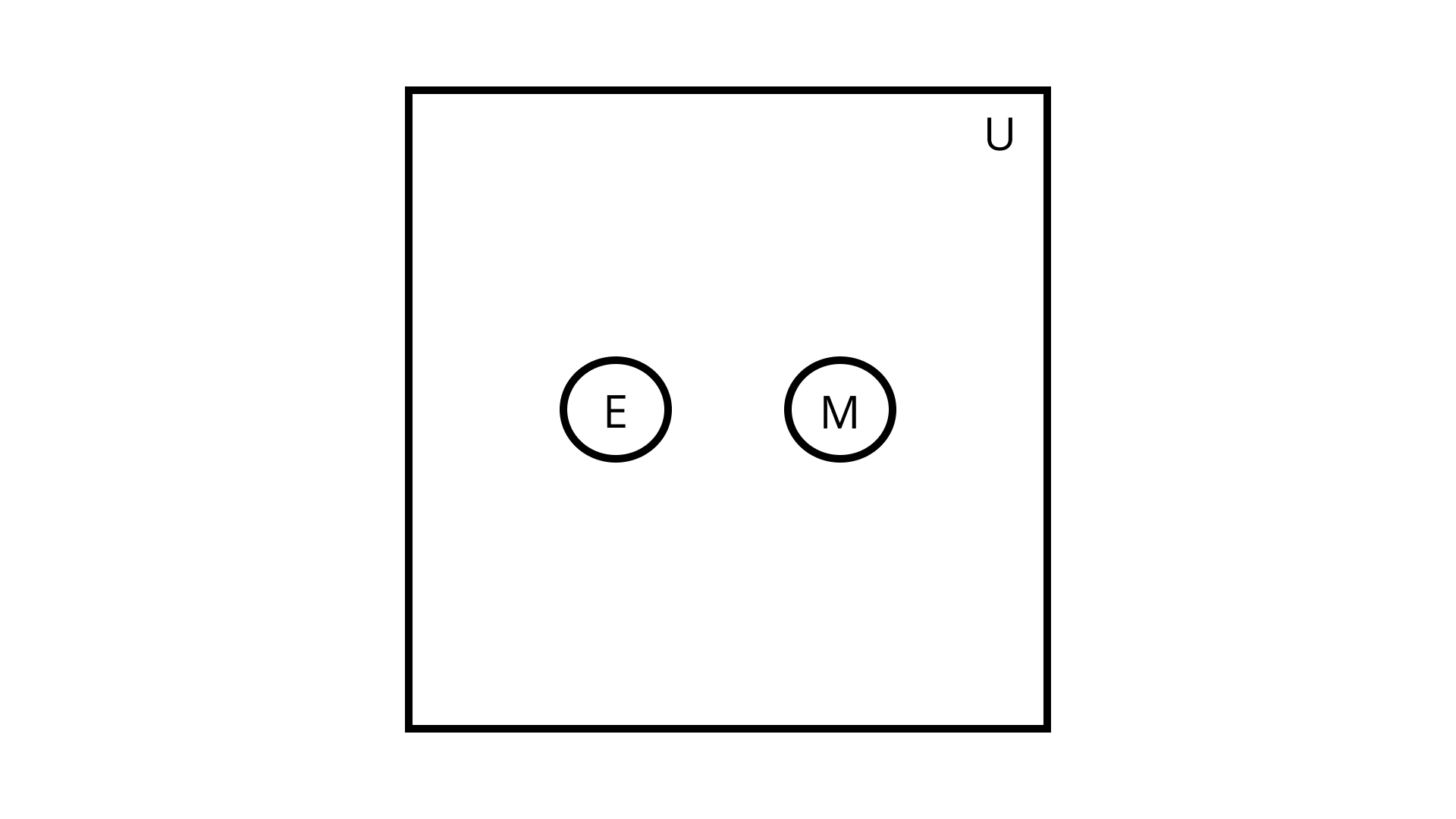
(ii) There is no student who studies both Mathematics and English.

Given: $\mathrm{E}, \mathrm{M}$ and $\mathrm{U}$ are sets.

To find: Relation between $\mathrm{E}, \mathrm{M}$ and $\mathrm{U}$ using Venn diagram.

Ans: Here, $\mathrm{E} \cap \mathrm{M}=\phi$.

Therefore, Venn diagram is

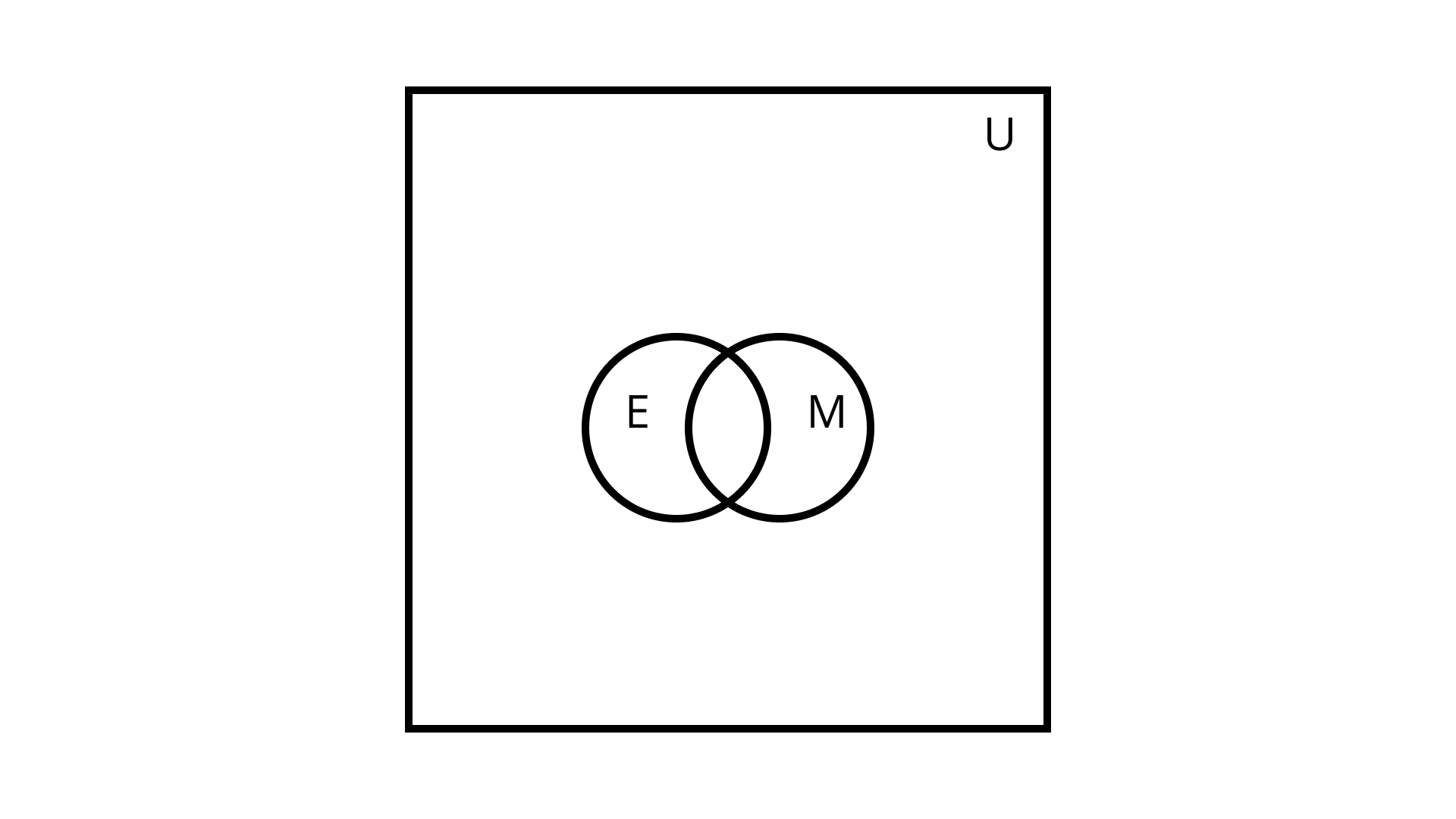
(iii) Some of the students study Mathematics but do not study English, some study English but do not study Mathematics, and some study both.

Given: E, M and U are sets.

To find: Relation between $\mathrm{E}, \mathrm{M}$ and $\mathrm{U}$ using Venn diagram. 

Ans: As there are some students who study English, Mathematics or both. Therefore, Venn diagram is  

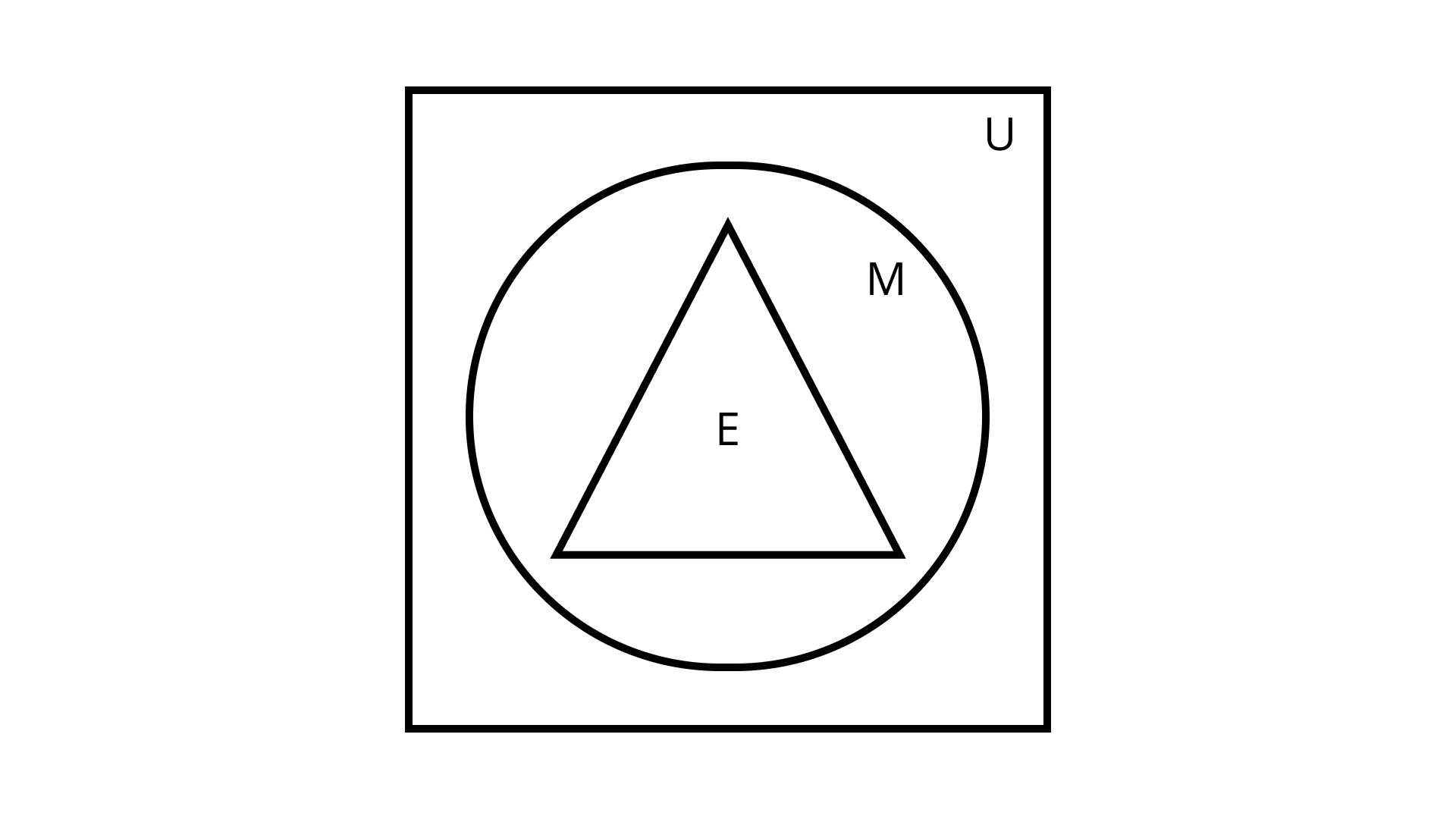
(iv) Not all students study Mathematics, but every student studying English studies Mathematics.

Given: $\mathrm{E}, \mathrm{M}$ and $\mathrm{U}$ are sets.

To find: Relation between E, M and U using Venn diagram.

Ans: Here, $\mathrm{E} \subset \mathrm{M} \subset \mathrm{U}$.

Therefore, Venn diagram is 

8. For all sets $A, B$ and $C$. Is( $A \cap B )\cup C=A \cap B \cup C ?$ Justify your statement.

Given: $\mathrm{A}, \mathrm{B}$ and $\mathrm{C}$ are sets.

To find: Justify $(A \cap B) \cup C=A \cap(B \cup C)$.

Ans:

Let,

$A=\{1,2\}$,

$B=\{2,3\}$,

$C=\{3,4\} .$

Taking L.H.S,

$(A \cap B) \cup C=(\{1,2\} \cap\{2,3\}) \cup\{3,4\}$

$(A \cap B) \cup C=(\{2\}) \cup\{3,4\}$

$(A \cap B) \cup C=(\{1,2\} \cap\{2,3\}) \cup\{3,4\}$

$(A \cap B) \cup C=\{2,3,4\}$

Now,

$A \cap(B \cup C)=\{1,2\} \cap(\{2,3\} \cup\{3,4\})$

$A \cap(B \cup C)=\{1,2\} \cap(\{2,3,4\})$

$A \cap(B \cup C)=\{2\}$

$\therefore(A \cap B) \cup C \neq A \cap(B \cup C) .$

9. Use the properties of sets to prove that for all the sets $A$ and $B$, $A-(A \cap B) = A-B$. 

Given: $A$ and $B$ are sets.

To find: Prove $A-(A \cap B)=A-B$.

 Ans:

Here

$A-(A \cap B)=A \cap(A \cap B)^{\prime} \quad\left\{A s,(A-B)=\left(A \cap B^{\prime}\right)\right\}$

$\Rightarrow A-(A \cap B)=A \cap\left(A^{\prime} \cup B^{\prime}\right) \quad\left\{A s,(A \cap B)^{\prime}=\left(A^{\prime} \cup B^{\prime}\right)\right\}$

$\Rightarrow A-(A \cap B)=\left(A \cap A^{\prime}\right) \cup\left(A \cap B^{\prime}\right)$

$\Rightarrow A-(A \cap B)=\phi \cup\left(A \cap B^{\prime}\right)$

$\Rightarrow A-(A \cap B)=A \cap B^{\prime}$

$\Rightarrow A-(A \cap B)=A-B$.

Long Answer Type

10. For all sets $A, B$ and $C$ . Is $(A-B) \cap (C-B) = (A \cap C)- B$ ? Justify your answer.

Given: $\mathrm{A}, \mathrm{B}$ and $\mathrm{C}$ are sets.

To find: Justify $(A-B) \cap(C-B)=(A \cap C)-B$. 

Ans:

Let $x \in(A-B) \cap(C-B)$

$\Rightarrow \mathrm{x} \in(\mathrm{A}-\mathrm{B})$ and $\mathrm{x}  \in(\mathrm{C}-\mathrm{B})$

$\Rightarrow(\mathrm{x} \in \mathrm{A}$ and $\mathrm{x} \notin \mathrm{B})$ and $(\mathrm{x} \in \mathrm{C}$ and $\mathrm{x} \notin \mathrm{B})$

$\Rightarrow(x \in A$ and $x \in C)$ and $x \notin B \quad\{$ using distributive law $\}$

$\Rightarrow x \in(A \cap C)-B$

$\therefore(A-B) \cap(C-B) \subset(A \cap C)-B$

Now,

Let $y \in(A \cap C)-B$

$\Rightarrow(\mathrm{y} \in \mathrm{A}$ and $\mathrm{y} \in \mathrm{C})$ and $\mathrm{y} \notin \mathrm{B}$

$\Rightarrow(\mathrm{y} \in \mathrm{A}$ and $\mathrm{y} \notin \mathrm{B})$ and $(\mathrm{y} \in \mathrm{C}$ and $\mathrm{y} \notin \mathrm{B}) \quad\{$ using distributive law $\}$

$\Rightarrow y \in(A-B)$ and $y \in(C-B)$

$\Rightarrow y \in(A-B) \cap(C-B)$

$\Rightarrow(A \cap C)-B \subset(A-B) \cap(C-B) \quad$-(ii)

from (i) and (ii), we get

$(A-B) \cap(C-B)=(A \cap C)-B .$

11. Let $A, B$ and $C$. Then show that $A \cup (B \cap C) = (A\cup B) \cap (A \cup C)$. 

Given: $\mathrm{A}, \mathrm{B}$ and $\mathrm{C}$ are sets.

To find: Show that, $A \cup(B \cap C)=(A \cup B) \cap(A \cup C)$.

Ans: 

Let $x \in A\cup (B \cap C)$

$\Rightarrow x \in A \text{ or } x\in B\cap C$

$\Rightarrow x \in A \text{ or } (x\in B \text{ and } x\in C)$

$\Rightarrow (x \in A \text{ or } x\in B) \text{ and } (x \in A \text{ or } x \in C)$

$\Rightarrow (x \in A\cup B) \text{ and } (x \in A\cup C)$

$\Rightarrow x \in (A\cup B)\cap( A\cup C)$

$\therefore A \cup (B \cap C) \subset(A\cup B)\cap( A\cup C)$---------(i)

Now,

Let $y \in (A\cup B)\cap( A\cup C)$

$y\in (A\cup B) \text{ and }( A\cup C)$

$\Rightarrow (y \in A \text{ or }y \in B)\text{ and } (y \in A \text{ or }y \in C)$

$\Rightarrow y \in A \text{ or } (y \in B \text{ and } y \in C)$

$\Rightarrow y\in A \text{ or } (y\in B\cap C)$

$\Rightarrow x\in A\cup(B\cap C)$

Therefore, $(A\cup B)\cap( A\cup C) \subset A\cup(B\cap C)$ ----------(ii)

From (i) and (ii), we get

$A \cup(B \cap C)=(A \cup B) \cap(A \cup C) .$

12. Let $P$ be the set of prime numbers and let $S=\left\{t \mid 2^{t}-1\right.$ is a prime $\}$. Prove that $S \subset P$.

Given:

P set of prime numbers,

$S=\left\{t \mid 2^{t}-1\right.$ is a prime $\} .$

To find: Prove that $S \subset P$.

Ans:

$P=\{2,3,5,7,11,13,17,19 \ldots .\}$

$S=\{2,3,5,7 \ldots \ldots .\} .$

Clearly, every element of $\mathrm{S}$ is also the element in $\mathrm{P}$.

Therefore, $\mathrm{S} \subset \mathrm{P}$.

Hence proved.

13. From 50 students taking examinations in Mathematics, Physics and Chemistry, each of the students has passed in at least one of the subjects, 37 passed Mathematics, 24 Physics and 43 Chemistry. At most 19 passed Mathematics and Physics, at most 29 Mathematics and Chemistry and at most 20 Physics and Chemistry. What is the largest possible number that could have passed all three examinations?

Ans: Let M be set of students passed in Mathematics,

$P$ be set of students passed in Physics,

C be a set of students passed in Chemistry.

Substitute values in the relation,

$n(M \cup P \cup C)=n(M)+n(P)+n(C)-n(M \cap P)-n(M \cap C)-n(P \cap C)+n(M \cap P \cap C)$

$37+24+43-19-29-20+n(M \cap P \cap C) \leq 50$

$n(M \cap P \cap C) \leq 50-36$

$\therefore \mathrm{n}(\mathrm{M} \cap \mathrm{P} \cap \mathrm{C}) \leq 14$

Objective Type Questions

Choose the correct answer from the given four options in each of the Examples 14 to 16 (M.C.Q.)

14. Each set $X_{r}$ contains 5 elements and each set $Y_{r}$ contains 2 elements and $\bigcup_{r=1}^{20} X_{r}=S=\bigcup_{r=1}^{n} Y_{r} .$ If each element of $S$ belongs to exactly 10 of the $X_{r}^{\prime} s$ and exactly 4 of $Y_{r}^{\prime} s$. Then, $n$ is

(A) 10

(B) 20

(C) 100

(D) 50

Ans: The Correct Answer is option B.

Given:

$X_{r}$ contains 5 elements,

$\mathrm{Y}_{\mathrm{r}}$ contains 2 elements and,

$\bigcup_{r=1}^{20} X_{r}=S=\bigcup_{r=1}^{n} Y_{r} .$

To find: $\mathrm{n}=$ ? 

If elements are not repeated, then number of elements in

$\mathrm{X}_{1} \cup \mathrm{X}_{2} \cup \mathrm{X}_{3} \ldots \ldots \cup \mathrm{X}_{20}$ is $20 \times 5$. But each element is used 10 times, so

$\mathrm{S}=\dfrac{20 \times 5}{10}$

S=10

If each element in $\mathrm{Y}_{1}, \mathrm{Y}_{2}, \mathrm{Y}_{3} \ldots \ldots \mathrm{Y}_{\mathrm{n}}$ are not repeated then total number of element in $2 \mathrm{n}$ but each element is repeated 4 times. So,

$\Rightarrow \mathrm{S}=\dfrac{2 \mathrm{n}}{4}$

$\Rightarrow 10=\dfrac{2 \mathrm{n}}{4}$

$\Rightarrow \mathrm{n}=20$

15. Two finite sets have $m$ and $n$ respectively. The total number of subsets of the first set is 56 more than the total number of subsets of the second set. The value of $\mathrm{m}$ and $\mathrm{n}$ respectively are:

(A) 7,6

(B) 5,1

(C) 6,3

(D) 8,7 .

Ans: The Correct Answer is option C.

Given: Two finite sets with $m$ and $n$ elements.

To find: The values of $m$ and $n$ are

$\mathrm{m}$=?

$\mathrm{n}$=?

Since, the number of subsets of a containing $m$ elements is 56 more than the subsets of the set containing $\mathrm{n}$ elements. 

$\Rightarrow 2^{\mathrm{m}}-2^{\mathrm{n}}=56$

$\Rightarrow 2^{\mathrm{n}}\left(2^{\mathrm{m-n}}-1\right)=2^{3} \cdot 7$

$\Rightarrow 2^{\mathrm{n}}=2^{3} \text { and } 2^{\mathrm{m-n}}-1=7$

$\Rightarrow \mathrm{n}=3 \text { and } 2^{\mathrm{m-n}}=8$

$\Rightarrow \mathrm{n}=3 \text { and } 2^{\mathrm{m-n}}=2^{3}$

$\Rightarrow \mathrm{m}-\mathrm{n}=3 \text { and } \mathrm{n}=3$

$\Rightarrow \mathrm{m}=6 \text { and } \mathrm{n}=3$

16. The set $(A \cup B \cup C) \cap\left(A \cap B^{\prime} \cap C^{\prime}\right)^{\prime} \cap C^{\prime}$ is equal to

(A) $B \cap C^{\prime}$

(B) $A \cap C$

(C) $B \cup C^{\prime}$

(D) $A \cap C$

 Ans: The correct option is A.

Given: A set.

To find: $(A \cup B \cup C) \cap\left(A \cap B^{\prime} \cap C^{\prime}\right)^{\prime} \cap C^{\prime}=?$

The set operations are as follows,

$=(A \cup(B \cup C)) \cap\left(A^{\prime} \cup(B \cup C)\right) \cap C^{\prime}$

$=\left(A \cap A^{\prime}\right) \cup(B \cup C) \cap C^{\prime}$

$=\phi \cup(B \cup C) \cap C^{\prime}$

$=B \cap C^{\prime} \cup \phi$

$=B \cap C^{\prime}$

Fill in the blanks 17 to $18 .$

17. If $\mathbf{A}$ and $\mathbf{B}$ are finite sets, then $\mathbf{n}(\mathbf{A})+\mathbf{n}(\mathbf{B})$ is equal to

Ans: Given: $A$ and $B$ are finite sets.

To find: $n(A)+n(B)=?$

$n(A \cup B)=n(A)+n(B)-n(A \cap B)$

$\therefore n(A)+n(B)=n(A \cup B)+n(A \cap B)$.

18. If $\mathbf{A}$ is a finite set containing $\mathrm{n}$ element, then the number of subsets of $\mathbf{A}$ is ____________ .

Ans: Given: Set $\mathrm{A}$ with $\mathrm{n}$ elements.

To find: Number of subsets of $\mathrm{A}$.

Let,

$\mathrm{A}=\{1\}$,

Subsets $=\{\phi\},\{1\}$

number of subsets $=2^{1}$.

$\mathrm{A}=\{0,1\} $

Subsets $=\{\phi\},\{0\},\{1\},\{0,1\}$

number of subsets $=2^{2}$.

$\therefore$ for $\mathrm{n}$ elements, number of subsets $=2^{\mathrm{n}}$.

State True or False 19 and $20 .$

19. Let $R$ and $S$ be the sets defined as follows,

$\mathrm{R}=\{\mathrm{x} \in \mathrm{Z} \mid \mathrm{x}$ is divisible by 2$\}$,

$\mathrm{S}=\{\mathrm{y} \in \mathrm{Z} \mid \mathrm{y}$ is divisible by 3$\} .$

then, $R \cap S=\phi$.

Ans: Given:

$\mathrm{R}=\{\mathrm{x} \in \mathrm{Z} \mid \mathrm{x}$ is divisible by 2$\}$,

$\mathrm{S}=\{\mathrm{y} \in \mathrm{Z} \mid \mathrm{y}$ is divisible by 3$\} .$

To find: True or false.

$\mathrm{R} \cap \mathrm{S} \neq \phi$.

Since, $\{6,12,18 \ldots .\}$ are divisible by both 2 and $3 . \mathrm{R} \cap \mathrm{S}$ can never be an empty set. Therefore, false. 

20. $Q \cap R=Q$, where $Q$ is the set of rational numbers and $R$ is the set of real numbers.

Ans: Given:

Q set of rational numbers,

R set of real numbers.

To find: True or false.

Since, every element of set $Q$ is also the element of set $R$. Every rational number is also a real number.

$\therefore Q \subset R$

$\Rightarrow \mathrm{Q} \cap \mathrm{R}=\mathrm{Q}$ .

Therefore, true.

EXERCISE 1.3

1. Write the following sets in roster form:

(i) $\quad A=\left\{x: x \in R, 2 x+11=15 \right\}.$

Ans: Given: Sets are given in set-builder form

$A=\{x: x \in R, 2 x+11=15\}$

To find: The following sets in roster form.

$A=\{x: x \in R, 2 x+11=15\}$

$2 x+11=15$

$\Rightarrow 2x=4$

$x=2$

Therefore, the set in roster form $\mathrm{A}=\{2\}$.

(ii) $\quad B=\{x \mid x^{2} = x, x \in R \}.$

Ans: Given: Set is given in set-builder form

To find: The following sets in roster form.

Given, $B=\left\{x \mid x^{2}=x, x \in R\right\}$

$\Rightarrow x^{2}=x$

$\Rightarrow x^{2}-x=0$

$\Rightarrow x(x-1)=0,$

$\Rightarrow x=0,1$ .

Therefore, the set in roster form $\mathrm{B}=\{0,1\}$.

(iii) $\quad C=\{x \mid x$ is a positive factor of a prime number $p\}$

Ans: Given: Set is given in set-builder form

To find: The following sets in roster form.

Given, $C=\{x \mid x$ is a positive factor of a prime number $p\} .$

The positive factor of any prime number $p$ is 1 and the number itself that is $p$.

Therefore, the set in roster form $C=\{1, p\}$.

2. Write the following sets in the roaster form:

(i) $D=\left\{t \mid t^{3}=t, t \in R\right\}$

Ans: Given: Set is in set builder form,

$D=\left\{t \mid t^{3}=t, t \in R\right\}$,

To find: The following sets in roster form.

Given, $D=\left\{t \mid t^{3}=t, t \in R\right\},$

$\Rightarrow t^{3}=t$

$\Rightarrow t^{3}-t=0$

$\Rightarrow t\left(t^{2}-1\right)=0$

$\Rightarrow t=-1,0,1$ .

Therefore, the set in roster form $D=\{-1,0,1\}$.

(ii) $E=\left\{w \mid \dfrac{w-2}{w+3}=3, w \in R\right\}$  

Ans: Given,

$E=\left\{w \mid \dfrac{w-2}{w+3}=3, w \in R\right\},$

$\Rightarrow \dfrac{w-2}{w+3}=3$

$\Rightarrow w-2=3 w+9$

$\Rightarrow 2 w=-11$

$\Rightarrow w=-\dfrac{11}{2}$ .

Therefore, the set in roster form $\mathrm{E}=\left\{-\dfrac{11}{2}\right\}$.

(iii) $F=\left\{x \mid x^{4}-5 x^{2}+6=0, x \in R\right\}$

Given set is in set builder form,

$F=\left\{x \mid x^{4}-5 x^{2}+6=0, x \in R\right\}$ .

To find: The following sets in roster form.

Ans: Given,

$F=\left\{x \mid x^{4}-5 x^{2}+6=0, x \in R\right\}$

$\Rightarrow x^{4}-5 x^{2}+6=0$

$\Rightarrow x^{4}-3 x^{2}-2 x^{2}+6=0$

$\Rightarrow x^{2}\left(x^{2}-3\right)-2\left(x^{2}-3\right)=0$

$\Rightarrow\left(x^{2}-3\right)\left(x^{2}-2\right)=0$

$\Rightarrow x=\pm \sqrt{3}, \pm \sqrt{2}$

Therefore, the set in roster form $\mathrm{F}=\{-\sqrt{3},-\sqrt{2}, \sqrt{2}, \sqrt{3}\}$.

3. If $Y=\left\{x \mid x \text{ is a positive factor of the number } 2^{p-1}(2^{p}-1), \text{where } 2^{p}-1 \text{ is a prime number } \right\}$. Write $\mathrm{Y}$ in the roaster form.

Given: A set

$\mathrm{Y}=\left\{\mathrm{x} \mid \mathrm{x}\right.$ is a positive factor of the number $2^{\mathrm{p}-1}\left(2^{\mathrm{p}}-1\right)$, where $\left(2^{\mathrm{p}}-1\right)$ is a prime number $\}$ in set builder form.

To find: The given set in roster form.

Ans: The factor of $2^{p-1}$ are $1,2,2^{2}, 2^{3} \ldots \ldots .2^{p-1} .$ since, $\left(2^{p}-1\right)$ is the prime number with factors 1 and $\left(2^{p}-1\right)$.

Therefore, the set in roster form $Y=\left\{1,2,2^{2}, 2^{3} \ldots \ldots . .2^{p-1}, 2^{p}-1\right\}$ 

4. State which of the following statements are true and which are false. Justify your answer.

(i) $35 \in \{x\mid x$ has exactly four positive factors $\}$.

Ans: Given,

$35 \in\{x \mid x$ has exactly four positive factors $\}$

The factors of 35 are 1, 5,7 and 35 .

Hence, the statement is true.

(ii) $128 \in\{y \mid$ the sum of all the positive factors of $y$ is $2 y\}$.

Ans: Given,

$128 \in\{y \mid$ the sum of all the positive factors of $y$ is $2 y\}$. The factors of 128 are $1,2,4,8,16,32,64,128$.

The sum of the factors is $1+2+4+8+16+32+64+128=255$ which is not equals to $2 y=2 \times 128=256$.

Therefore, the statement is false.

(iii) $3 \notin \left\{x \mid x^{4}-5 x^{3}+2 x^{2}-112 x+6=0\right\} .$

Ans: Given,

$3 \notin \left\{x \mid x^{4}-5 x^{3}+2 x^{2}-112 x+6=0\right\} .$

Substitute $x=3$, in $x^{4}-5 x^{3}+2 x^{2}-112 x+6=0$. At $x=3$,

$(3)^{4}-5(3)^{3}+2(3)^{2}-112(3)+6=0$

$\Rightarrow-346=0$

Therefore, the statement is true.

(iv) $496 \notin\{y \mid$ the sum of all the positive factors of y is $2 y\}$.

Ans: Given, $496 \notin\{y \mid$ the sum of all the positive factors of y is $2 y\}$.

The factors of 496 are 1, 2, 4, 8, 16, 31, 62, 124, 248, 496 .

The sum of the factors is $1+2+4+8+16+31+62+124+248+496=992$ which is equal to $2 y=2 \times 496=992$.

Therefore, the statement is false.

5. Given, $\mathrm{L}=\{1,2,3,4\}, \mathrm{M}=\{3,4,5,6\}$ and $\mathrm{N}=\{1,3,5\}$. Verify that $L-(M \cup N) = (L-M) \cap (L-N)$

Given: Three sets are given as,

$\mathrm{L}=\{1,2,3,4\}, \mathrm{M}=\{3,4,5,6\}$ and $\mathrm{N}=\{1,3,5\} .$

To find: obtain $\mathrm{L}-(\mathrm{M} \cup \mathrm{N})$ and $(\mathrm{L}-\mathrm{M}) \cap(\mathrm{L}-\mathrm{N})$ then verify them.

Ans: Calculate: L - $(M \cup N)$

$\Rightarrow \mathrm{L}-(\mathrm{M} \cup \mathrm{N})=\{1,2,3,4\}-\{3,4,5,6\} \cup\{1,3,5\}$

$\Rightarrow \mathrm{L}-(\mathrm{M} \cup \mathrm{N})=\{1,2,3,4\}-\{1,3,4,5,6\}$

$\Rightarrow \mathrm{L}-(\mathrm{M} \cup \mathrm{N})=\{2\}$ .

Calculate: $(\mathrm{L}-\mathrm{M}) \cap(\mathrm{L}-\mathrm{N})$

$(\mathrm{L}-\mathrm{M}) \cap(\mathrm{L}-\mathrm{N})=(\{1,2,3,4\}-\{3,4,5,6\}) \cap(\{1,2,3,4\}-\{1,3,5\})$

$\Rightarrow(\mathrm{L}-\mathrm{M}) \cap(\mathrm{L}-\mathrm{N})=\{1,2\} \cap\{2,4\}=\{2\}$.

Now, $L-(M \cup N)$ and $(L-M) \cap(L-N)$ Both sets are equal.

Verified $\mathrm{L}-(\mathrm{M} \cup \mathrm{N})=(\mathrm{L}-\mathrm{M}) \cap(\mathrm{L}-\mathrm{N})$.

6. If $A$ and $B$ are subsets of the universal set $U$, then show that

(i) $A \subset A \cup B$ 

Given: The universal set $U, A$ and $B$ are subsets of the universal set $U$ which can be expressed as $\mathrm{A} \subset \mathrm{U}$ and $\mathrm{B} \subset \mathrm{U} . $

To find:

Show that: $A \subset A \cup B$

Ans: To show that $A \subset A \cup B$, .

Let us consider that $x \in A$..

If $\mathrm{x} \in \mathrm{A}$ then $\mathrm{x}$ is the element in set $\mathrm{A}$..

Now, $x \in(A \cup B)$ as $x \in A$ or $x \in B$.

This implies that $A \subset A \cup B$.

(ii) $A \subset B \Leftrightarrow A \cup B=B$

Given: The universal set $\mathrm{U}, \mathrm{A}$ and $\mathrm{B}$ are subsets of the universal set $\mathrm{U}$ which can be expressed as $\mathrm{A} \subset \mathrm{U}$ and $\mathrm{B} \subset \mathrm{U} . .$

To find:

Show that: $A \subset B \Leftrightarrow A \cup B=B$

Ans: It is given that $A \subset B$. So consider that $x \in(A \cup B)$.

From this condition either $\mathrm{x} \in \mathrm{A}$ or $\mathrm{x} \in \mathrm{B}$.

As $A \subset B$ this directly implies that $x \in B$.

From the above conclusions,

$A \cup B \subset B \quad--------(1)$ and $B \subset A \cup B \quad---------(2)$.

From -(1) and -(2) $A \cup B=B$.

If $A \cup B=B$ then consider $y \in A$, which implies that $y \in(A \cup B)$.

$y \in(A \cup B)$

$\Rightarrow y \in B$

$\Rightarrow A \subset B$

$\text { Hence, } A \subset B \Leftrightarrow A \cup B=B$ .

(iii) $(A \cap B) \subset A$

Given: The universal set U, A and B are subsets of the universal set U which can be expressed as $\mathrm{A} \subset \mathrm{U}$ and $\mathrm{B} \subset \mathrm{U} . .$

To find:

Show that: $(A \cap B) \subset A$

Ans: Let us consider $x \in(A \cap B)$,

$\Rightarrow \mathrm{X} \in \mathrm{A}$ and $\mathrm{x} \in \mathrm{B}$

$\Rightarrow \mathrm{X} \in \mathrm{A}$

Hence, $(A \cap B) \subset A$.

7. Given that $\mathbf{N}=\{1,2,3 \ldots \ldots \ldots 100\}$. Then write

(i) The subset of $\mathrm{N}$ whose elements are even numbers.

Given: The set in Roster form $\mathrm{N}=\{1,2,3 \ldots \ldots \ldots .100\}$.

To find:

The subset of $\mathrm{N}$ whose elements are even numbers

Ans: The subset of $\mathrm{N}$ whose elements are even numbers is $\{2,4,6 \ldots \ldots \ldots 100\}$. This set is the subset of $\mathrm{N}=\{1,2,3 \ldots \ldots \ldots 100\}$.

(ii) The subset of $\mathrm{N}$ whose elements are perfect square numbers

Given: The set in Roster form $\mathrm{N}=\{1,2,3 \ldots \ldots \ldots .100\}$.

To find:

The subset of $\mathrm{N}$ whose elements are perfect square numbers.

Ans: The set of perfect square numbers is $\{1,4,9,16,25,36,49,64,81,100\}$ and this set is subset of $\mathrm{N}=\{1,2,3 \ldots \ldots \ldots . .100\}$.

8. If $X=\{1,2,3\}$, if $n$ represents any member of $X$, write the following sets containing all numbers represented by 

(i). $4n$

Given: A set $X=\{1,2,3\}$ and $\mathrm{n}$ represents any member of $X$.

To find: The set which contains the numbers represented by the given relation.

Ans: Substituting each and every member $X=\{1,2,3\}$ in the relation $4 \mathrm{n}$. We get

$\{4 n \mid n \in X\}=\{4 \times 1,4 \times 2,4 \times 3\}=\{4,8,12\} .$

(ii) $\mathbf{n}+\mathbf{6}$

Given: A set $X=\{1,2,3\}$ and $n$ represents any member of $X$.

To find: The set which contains the numbers represented by the given relation.

 Ans: Substituting each and every member of $X=\{1,2,3\}$ in the relation $n+6$. We get,

$\{\mathrm{n}+6 \mid \mathrm{n} \in \mathrm{X}\}=\{1+6,2+6,3+6\}=\{7,8,9\}.$

(iii) $\dfrac{\mathrm{n}}{2}$

Given: A set $X=\{1,2,3\}$ and $\mathrm{n}$ represents any member of $X$.

To find: The set which contains the numbers represented by the given relation.

Ans: Substituting each and every member of $X=\{1,2,3\}$ in the relation $\dfrac{n}{2}$. We get,

$\left\{\dfrac{n}{2} \mid n \in X\right\}=\left\{\dfrac{1}{2}, \dfrac{2}{2}, \dfrac{3}{2}\right\}=\left\{\dfrac{1}{2}, 1, \dfrac{3}{2}\right\}.$

(iv) $\mathrm{n}-1$

Given: A set $X=\{1,2,3\}$ and $n$ represents any member of $X$.

To find: The set which contains the numbers represented by the given relation.

Ans: Substituting each and every member $X=\{1,2,3\}$ of in the relation $n-1$. We get,

$\{\mathrm{n}-1 \mid \mathrm{n} \in \mathrm{X}\}=\{1-1,2-1,3-1\}=\{0,1,2\}$.

9. If $\mathbf{Y}=\{1,2,3, \ldots . .10\}$, and a represents any element of $\mathbf{Y}$, write the following sets, containing all the elements satisfying the given conditions.

(i) $a \in Y$ but $a^{2} \notin Y$

Given: A set $\mathrm{Y}=\{1,2,3, \ldots . .10\}$ and a represents any element of $\mathrm{Y}$.

To find: The set which contains the numbers represented by the given relation.

Ans: Here $1^{2}, 2^{2}, 3^{2} \in \mathrm{Y}$. Therefore, the set $\left\{\mathrm{a} \mid \mathrm{a} \in \mathrm{Y}\right.$ but $\left.\mathrm{a}^{2} \notin \mathrm{Y}\right\}=\{4,5,6,7,8,10\}$.

(ii) $a+1=6, a \in Y$

Given: A set $\mathrm{Y}=\{1,2,3, \ldots .10\}$ and a represents any element of $\mathrm{Y}$.

To find: The set which contains the numbers represented by the given relation.

Ans: The set for the condition $\mathrm{a}+1=6, \mathrm{a} \in \mathrm{Y}$ is $\mathrm{a}=6-1=5$, $\mathrm{a} \in \mathrm{Y}$. Therefore,

$\{\mathrm{a} \mid \mathrm{a}+1=6, \mathrm{a} \in \mathrm{Y}\}=\{5\}$

(iii) a less than 6 and, $a \in Y$

Given: A set $\mathrm{Y}=\{1,2,3, \ldots . .10\}$ and a represents any element of $\mathrm{Y}$. 

To find: The set which contains the numbers represented by the given relation.

Ans: The set for the condition a is less than 6 and, $a \in Y$ is $a=\{1,2,3,4,5\}$. Therefore, $\{\mathrm{a} \mid \mathrm{a}$ less than 6 and, $\mathrm{a} \in \mathrm{Y}\}=\{1,2,3,4,5\}$.

10.  $A, B$ and $C$ are subsets of Universal Set U

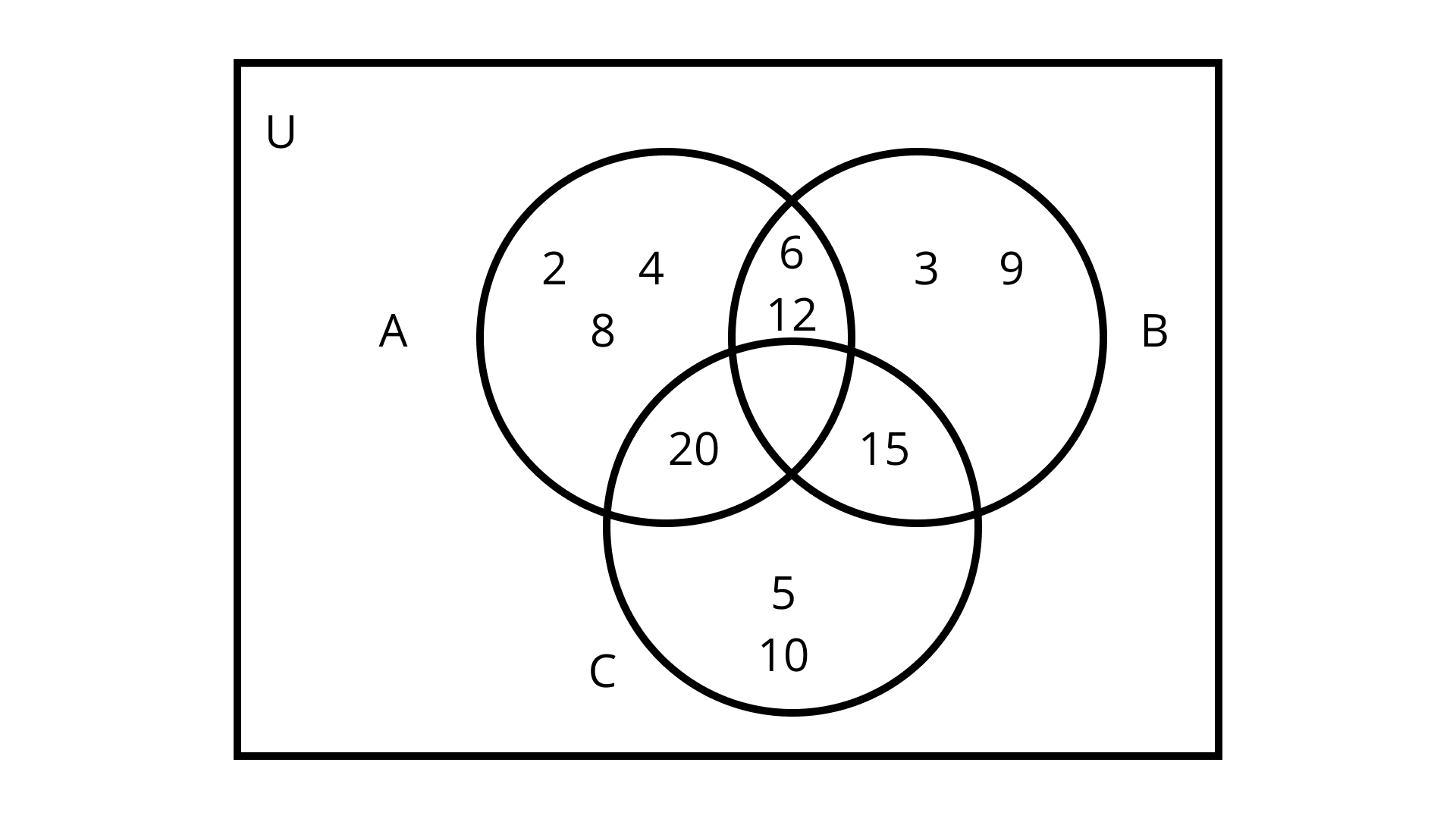
If $A=\{2,4,6,8,12,20\}, B=\{3,6,9,12,15\}, C=\{5,10,15,20\}$ and $U$ is the set of all whole numbers, draw a Venn diagram showing the relation of $U, A, B$ and $C$.

Given: $A=\{2,4,6,8,12,20\}, B=\{3,6,9,12,15\}, C=\{5,10,15,20\}$ and $U$ set of all whole numbers.

To find: The relation between sets $\mathrm{U}, \mathrm{A}, \mathrm{B}$ and $\mathrm{C}$ using the Venn diagram.

Ans: According to the given sets place the elements of sets in their respective circles

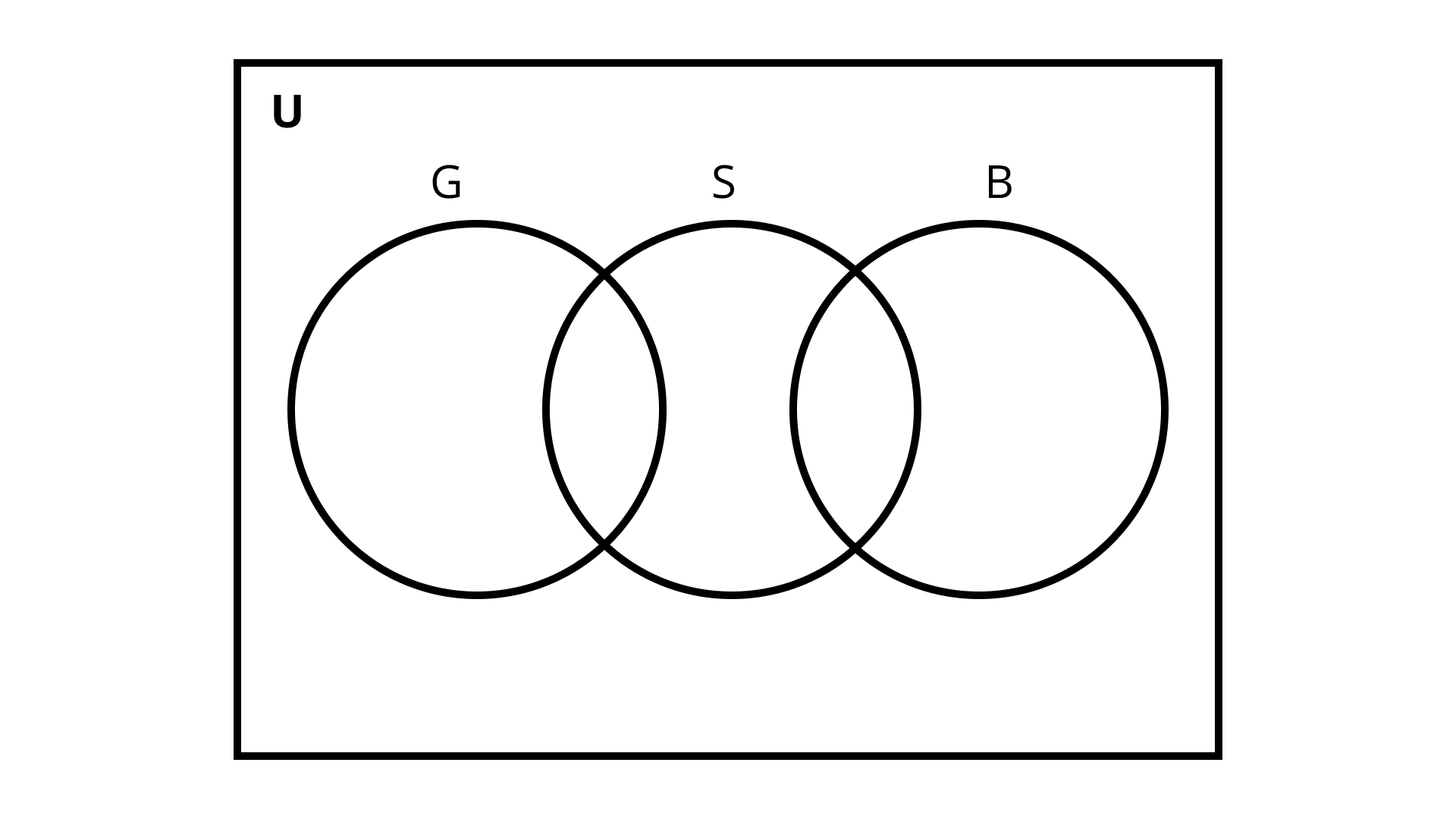
11. Let $U$ be the set of all boys and girls in a school, $G$ be the set of all girls in the school, B be the set of all boys in the school, and $\mathrm{S}$ be the set of all students in the school who take swimming. Some, but not all, students in the school take swimming lessons. Draw a Venn diagram showing one of the possible interrelationships among sets $\mathbf{U}, \mathbf{G}, \mathbf{B}$ and $\mathbf{S}$.

Given: $U$ set of all boys and girls in a school, $G$ be the set of all girls, B be the set of all boys and $S$ the set of all students in the school who take swimming.

To find: The relationship among sets $\mathrm{U}, \mathrm{G}, \mathrm{B}$ and $\mathrm{S}$ using the Venn diagram.

Ans: B represents the set of all boys in school, $G$ represents the set of all girls in school and S represents the set of all students in the school who take swimming. It is given that not all students take swimming. Therefore, some of them are boys and the rest are girls. 

12. For all sets $A, B$ and $C$, show that $(A-B) \cap(A-C)=A-(B \cup C)$.

Given: $A, B$ and $C$ are the sets.

To find: show that $(A-B) \cap(A-C)=A-(B \cup C)$.

Ans: Taking L.H.S $(\mathrm{A}-\mathrm{B}) \cap(\mathrm{A}-\mathrm{C})$,

Let us consider that $\mathrm{x} \in(\mathrm{A}-\mathrm{B}) \cap(\mathrm{A}-\mathrm{C})$,

using basic definition of operations of sets we get,

$\Rightarrow \mathrm{X} \in(\mathrm{A}-\mathrm{B})$ and $\mathrm{x} \in(\mathrm{A}-\mathrm{C})$

$\Rightarrow(\mathrm{x} \in \mathrm{A}$ and $\mathrm{x} \notin \mathrm{B}) \cap(\mathrm{x} \in \mathrm{A}$ and $\mathrm{x} \notin \mathrm{C})$

$\Rightarrow \mathrm{x} \in \mathrm{A}$ and $(\mathrm{x} \notin \mathrm{B}$ and $\mathrm{x} \notin \mathrm{C})$

$\Rightarrow \mathrm{x} \in \mathrm{A}$ and $\mathrm{x} \notin(\mathrm{B} \cup \mathrm{C})$

$\Rightarrow x \in A-(B \cup C)$

This implies that $\mathrm{x} \in(\mathrm{A}-\mathrm{B}) \cap(\mathrm{A}-\mathrm{C}) \subseteq \mathrm{A}-(\mathrm{B} \cup \mathrm{C})---------------(1)$.

Taking R.H.S=  A - (B $\cup \mathrm{C}$ ),

Let us consider the element $y \in A-(B \cup C)$,

using basic definition of operations of sets we get,

$\Rightarrow \mathrm{y} \in \mathrm{A}$ and $\mathrm{y} \notin(\mathrm{B} \cup \mathrm{C})$

$\Rightarrow \mathrm{y} \in \mathrm{A}$ and $(\mathrm{y} \notin \mathrm{B}$ and $\mathrm{y} \notin \mathrm{C})$

$\Rightarrow(\mathrm{y} \in \mathrm{A}$ and $\mathrm{y} \notin \mathrm{B})$ and $(\mathrm{y} \in \mathrm{A}$ and $\mathrm{y} \notin \mathrm{C})$

$\Rightarrow y \in(A-B)$ and $y \in(A-C)$

$\Rightarrow y \in(A-B) \cap(A-C)$

This implies that $y \in A-(B \cup C) \subseteq y \in(A-B) \cap(A-C) \quad------(2)$ 

By comparing -(1) and -(2) we get,

$(A-B) \cap(A-C)=A-(B \cup C) .$

Determine whether each of the statements in Exercises $13-17$ is true or false. Justify your answer.

13. For all sets $A$ and $B, (A-B) \cup (A \cap B) = A$.

Ans: Taking L.H.S $(\mathrm{A}-\mathrm{B}) \cup(\mathrm{A} \cap \mathrm{B})$

Using distributive law we get,

$[(A-B) \cup A] \cap[(A-B) \cup B]$

This implies that, $[\mathrm{A}] \cap[(\mathrm{A}-\mathrm{B})]$.

Now using the intersection and difference operation on sets we get,

$A \cap(A-B)=A$.

Therefore, the statement is true.

14. For all sets $\mathbf{A}, \mathbf{B}$ and $\mathbf{C}, \mathbf{A}-(\mathbf{B}-\mathbf{C})=(\mathbf{A}-\mathbf{B})-\mathbf{C}$.

Ans: Let $\mathrm{A}=\{1,2,3\}, \mathrm{B}=\{2,3,4\}, \mathrm{C}=\{4,1,5\}$.

Considering these sets and substituting in $A-(B-C)=(A-B)-C$ we get,

$\{1,2,3\}-(\{2,3,4\}-\{4,1,5\})=(\{1,2,3\}-\{2,3,4\})-\{4,1,5\}$

$\{1,2,3\}-(\{2,3\})=(\{1\})-\{4,1,5\}$

$\Rightarrow\{1\}=\phi$

Therefore, the statement is false.

15. For all sets $A, B$ and $C$, if $ A \subset B$, then $A \cap C \subset B \cap C$.

Ans: Let us consider that $x \in A \cap C$.

This implies that $x \in A$ and $x \in C$.

It is given that $A \subset B$.

Therefore, $\mathrm{x} \in \mathrm{B}$ and $\mathrm{x} \in \mathrm{C}$, 

$\Rightarrow \mathrm{x} \in \mathrm{B} \text { and } \mathrm{x} \in \mathrm{C}$

$\Rightarrow \mathrm{x} \in(\mathrm{B} \cap \mathrm{C})$

$\Rightarrow \mathrm{A} \cap \mathrm{C} \in(\mathrm{B} \cap \mathrm{C})$

$\Rightarrow \mathrm{A} \cap \mathrm{C} \subset(\mathrm{B} \cap \mathrm{C})$

Therefore, the statement is true.

16. For all sets $A, B$ and $C$, if $A \subset B$, then $A \cup C \subset B \cup C$.

Ans: Let us consider that $x \in A \cup C$.

This implies that $x \in A$ or $x \in C$,

It is given that $A \subset B$. Therefore, $x \in B$ or $x \in C$. So,

$\Rightarrow \mathrm{X} \in \mathrm{B}$ or $\mathrm{x} \in \mathrm{C}$

$\Rightarrow \mathrm{x} \in(\mathrm{B} \cup \mathrm{C})$

$\Rightarrow(A \cup C) \subset(B \cup C)$

Therefore, the statement is true.

17.For all sets $A, B$ and $C$, if $A \subset C$ and $B \subset C$, then $A \cup B \subset C$

Ans: Let us consider $\mathrm{X} \in \mathrm{A} \cup \mathrm{B}$.

This implies that $x \in A$ or $x \in B$.

It is given that $A \subset C$ and $B \subset C$.

Therefore, $x \in C$ or $x \in C$

$\Rightarrow x \in C$ or $x \in C$

$\Rightarrow \mathrm{X} \in \mathrm{C}$

$\Rightarrow \mathrm{A} \cup \mathrm{B} \subset \mathrm{C}$

Therefore, the statement is true.

Using Properties of sets Prove the Statements given in Exercises 18 to $22 .$

18. For all sets $A$ and $B$, $A \cup(B-A)=A \cup B$.

Given: $A$ and $B$ are two sets.

To find: To prove the statement $A \cup(B-A)=A \cup B$.

Ans: Taking L.H.S= A $\cup(B-A)$

Using the property $\mathrm{A}-\mathrm{B}=\mathrm{A} \cap \mathrm{B}^{\prime}$ we get,

$\Rightarrow \mathrm{A} \cup(\mathrm{B}-\mathrm{A})=\mathrm{A} \cup\left(\mathrm{B} \cap \mathrm{A}^{\prime}\right)$

Using distributive law,

$\Rightarrow A \cup\left(B \cap A^{\prime}\right)=(A \cup B) \cap\left(A \cup A^{\prime}\right)$

Now using complement law $\mathrm{A} \cup \mathrm{A}^{\prime}=\mathrm{U}$. We get,

$\Rightarrow(\mathrm{A} \cup \mathrm{B}) \cap(\mathrm{U})$

Now using property $\mathrm{A} \cap \mathrm{U}=\mathrm{A}$. We get,

$\Rightarrow(A \cup B) \cap(U)=A \cup B$ which is equals to R.H.S

Hence Proved, $(A \cup B) \cap(U)=A \cup B$.

19. For all sets $A$ and $B$, $A-(A-B) = A\cap B$

Given: $A$ and $B$ are two sets.

To find: To prove the statement $A-(A-B)=A \cap B$.

Ans: Taking R.H.S A - (A - B )

Using the property $A-B=A \cap B^{\prime}$ we get,

$=A-\left(A \cap B^{\prime}\right)$

Again, $A-B=A \cap B^{\prime}$ we get,

$=A \cap\left(A \cap B^{\prime}\right)^{\prime}$

Using DE Morgan's law $(A \cap B)^{\prime}=A^{\prime} \cup B^{\prime}$ we get,

$=A \cap\left(A^{\prime} \cup\left(B^{\prime}\right)^{\prime}\right)$

$=A \cap\left(A^{\prime} \cup B\right)$

Using distributive law we get,

$=\left(A \cap A^{\prime}\right) \cup(A \cap B)$

Using properties of intersection we get,

$=\Phi \cup(A \cap B)$

$=(A \cap B)$

Hence proved, $A-(A-B)=A \cap B$.

20. For all sets $A$ and $B, A-(A \cap B) =A-B$

Given: $\mathrm{A}$ and $\mathrm{B}$ are two sets. To find: To prove the statement $A-(A \cap B)=A-B$.

Ans: Taking L.H.S = A - (A $\cap$ B )

Using the property $A-B=A \cap B^{\prime}$ we get,

$A-(A \cap B)=A \cap(A \cap B)^{\prime}$

Using $D E$ Morgan's law $(A \cap B)^{\prime}=A^{\prime} \cup B^{\prime}$ we get,

$A \cap(A \cap B)^{\prime}=A \cap\left(A^{\prime} \cup B^{\prime}\right)$

Using distributive law we get,

$A \cap\left(A^{\prime} \cup B^{\prime}\right)=\left(A \cap A^{\prime}\right) \cup\left(A \cap B^{\prime}\right)$

$\left(A \cap A^{\prime}\right) \cup\left(A \cap B^{\prime}\right)=\Phi \cup\left(A \cap B^{\prime}\right)=\left(A \cap B^{\prime}\right)$

Using the property $A-B=A \cap B^{\prime}$ and we get,

$\left(A \cap B^{\prime}\right)=A-B$

Hence proved, $A-(A \cap B)=A-B$.

21. For all sets $A$ and $B, (A \cup B)-B=A-B$.

Given: $A$ and $B$ are two sets.

To find: To prove the statement $(A \cup B)-B=A-B$.

Ans: Taking L.H.S $(\mathrm{A} \cup \mathrm{B})-\mathrm{B}$

Using the property $(A-B)=A \cap B^{\prime}$ we get,

$=(A \cup B) \cap B^{\prime}$

Using distributive law we get,

$=\left(A \cap B^{\prime}\right) \cup\left(B \cap B^{\prime}\right)$

$=\left(A \cap B^{\prime}\right) \cup \Phi$

$=\left(A \cap B^{\prime}\right)$

$=A-B$

Hence proved, $(A \cup B)-B=A-B$.

22. Let $T=\left\{x \mid \dfrac{x+5}{x-7}-5=\dfrac{4 x-40}{13-x}\right\}$. Is $T$ an empty set? Justify your answer. 

Given: Set $\mathrm{T}=\left\{\mathrm{x} \mid \dfrac{\mathrm{x}+5}{\mathrm{x}-7}-5=\dfrac{4 \mathrm{x}-40}{13-\mathrm{x}}\right\} .$

To find: $\mathrm{T}$ is an empty set or not.

Ans: We have, $\mathrm{T}=\left\{\mathrm{x} \mid \dfrac{\mathrm{x}+5}{\mathrm{x}-7}-5=\dfrac{4 \mathrm{x}-40}{13-\mathrm{x}}\right\}$

$\Rightarrow \dfrac{x+5}{x-7}-5=\dfrac{4 x-40}{13-x}$

$\Rightarrow \dfrac{x+5-5(x-7)}{x-7}=\dfrac{4 x-40}{13-x}$

$\Rightarrow \dfrac{x+5-5 x+35}{x-7}=\dfrac{4 x-40}{13-x}$

$\Rightarrow \dfrac{-4 x+40}{x-7}=\dfrac{4 x-40}{13-x}$

$\Rightarrow-(4 x-40)(13-x)=(4 x-40)(x-7)$

$\Rightarrow (4 x-40)(x-7)+(4 x-40)(13-x)=0$

$\Rightarrow \mathrm{x}-10=0 \Leftrightarrow \mathrm{x}=10$

The obtained set is $\mathrm{T}=\{10\}$. Hence, $\mathrm{T}$ is not an empty set

Long Answer Type

23. Let $A, B$ and $C$ be sets. Then show that $A \cap(B \cup C)=(A \cap B) \cup(A \cap C)$.

Given: $A, B$ and $C$ are sets.

To find: show that $A \cap(B \cup C)=(A \cap B) \cup(A \cap C)$.

Ans: Let us consider, $x \in A \cap(B \cup C)$

$\Rightarrow \mathrm{x} \in \mathrm{A}$ and $\mathrm{x} \in(\mathrm{B} \cup \mathrm{C})$

$\Rightarrow \mathrm{x} \in \mathrm{A}$ and $(\mathrm{x} \in \mathrm{B}$ or $\mathrm{x} \in \mathrm{C})$

Using distributive law,

$\Rightarrow(x \in A$ and $x \in B)$ or $(x \in A$ and $x \in C)$

$\Rightarrow x \in(A \cap B)$ or $x \in(A \cap C)$

$\Rightarrow x \in(A \cap B) \cup(A \cap C)$

From above consideration, $x \in A \cap(B \cup C)$ we get, 

$A \cap(B \cup C) \subseteq(A \cap B) \cup(A \cap C)------------(1)$

$\text { Let us consider, } y \in(A \cap B) \cup(A \cap C)$

$\Rightarrow y \in(A \text { and } B) \text { or } y \in(A \text { and } C)$

$\Rightarrow y \in A \text { and } y \in(B \text { or } C)$

$\Rightarrow y \in A \cap(B \cup C)$

From above consideration, $y \in(A \cap B) \cup(A \cap C)$ we get,

$(A \cap B) \cup(A \cap C) \subseteq A \cap(B \cup C) \quad-----------(2)$

From (1) and (2) we get,

$A \cap(B \cup C)=(A \cap B) \cup(A \cap C)$

24. Out of 100 students 15 passed in English, 12 passed in Mathematics, 8 in Science, 6 in English and Mathematics, 7 in Mathematics and Science; 4 in English and Science; 4 in all the three. Find how many passed,

(i) In English and Mathematics but not in Science

(ii) In Mathematics and Science but not in English

(iii) In Mathematics only

(iv) In more than one subject only

Given:

$n(U)=100, n(E)=15, n(M)=12, n(S)=8, n(E \cap M)=6, n(E \cap S)=4, n(M \cap S)=7$

$, n(E \cap M \cap S)=4$

To find: number of students passed.

Ans: Let us consider that $M, E$ and $S$ be the sets which represent the number of students passed in Mathematics, English and science respectively.

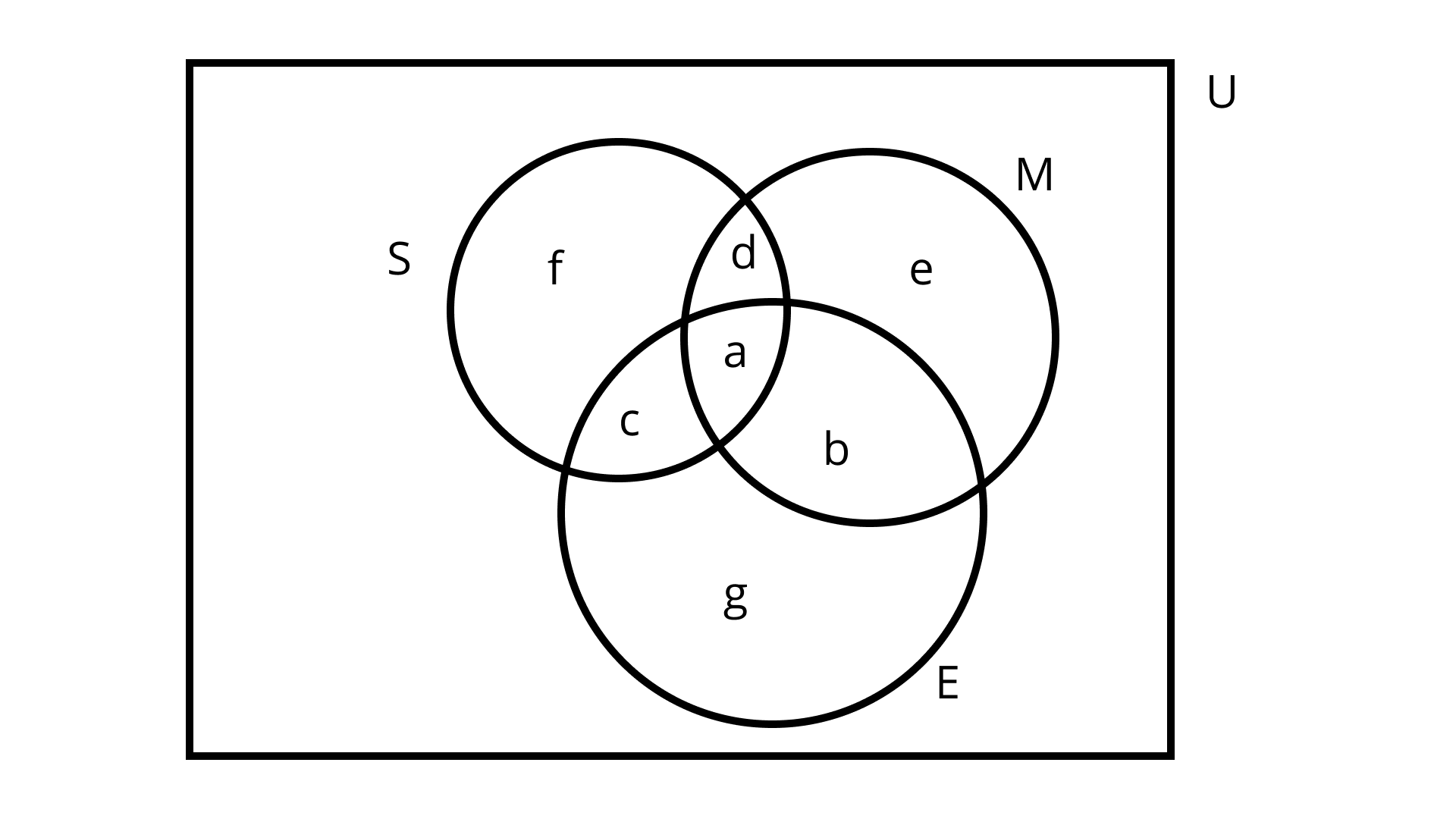
Using the Venn diagram assigning given values,

$n(E \cap M \cap S)=a=4, n(M \cap S)=a+d=7, n(M \cap E)=a+b=6, n(S \cap E)=a+c=4$

Some more values are,

$n(M)=a+b+d+e=12, n(E)=a+b+c+g=15, n(S)=a+c+d+f=8$

From the above relations we get, $a=4, b=2, c=0, d=3, e=3, f=1, g=9$.

(i) $\mathrm{b}$ represents the number of students passed in English and Mathematics but not in Science. So, the number of students passed is $b=2$.

(ii) $d$ represents the number of students passed in Mathematics and Science but not in English. So, the number of students passed is $d=3$.

(iii) e represents the number of students passed in Mathematics only. So, the number of students passed is $e=3$.

(iv) Number of students passed in more than one subject only is $a+b+c+d=9$.

25. In a class of 60 students, 25 students play cricket and 20 students play tennis, and 10 students play both the games. Find the number of students who play neither?

Given: $n(U)=60, n(C)=25, n(T)=20$ and $n(C \cap T)=10$.

To find: number of students who play neither cricket or tennis $=n(C \cup T)^{\prime}=?$

Ans:

Let, $\mathrm{C}$ be the set of students who play cricket and $\mathrm{T}$ be the set of students who play tennis.

Now, using important results of two sets, substitute the values in the formula,

$n(C \cup T)=n(C)+n(T)-n(C \cap T)$

$n(C \cup T)=25+20-10$

$n(C \cup T)=35$

Now, remove the number of students who play cricket or tennis from the universal set that is the total number of students in class.

The number of students who play neither is $n(C \cup T)^{\prime}=n(U)-n(C \cup T)=60-35=25$.

26. In a survey of 200 students of a school, it was found that 120 study Mathematics, 90 study Physics and 70 study Chemistry, 40 study Mathematics and Physics, 30 study Physics and Chemistry, 50 study Chemistry and Mathematics and 20 none of these subjects. Find the number of students who study all the three subjects.

Given:

$n(U)=200, n(M)=120, n(P)=90, n(C)=70, n(M \cap P)=40, n(P \cap C)=30, n(C \cap M)=50$, $n(U)-n(M \cup P \cup C)=20 .$

Where, $M, P$ and $C$ represent a set of mathematics, physics and chemistry.

To find: $n(M \cap P \cap C)=?$

 Ans:

$n(U)-n(M \cup P \cup C)=20 \Leftrightarrow n(M \cup P \cup C)=n(U)-20$

$n(M \cup P \cup C)=200-20=180$

Using the relation and substituting values we get,

$n(M \cup P \cup C)=n(M)+n(P)+n(C)-n(M \cap P)-n(P \cap C)-n(C \cap M)+n(M \cap P \cap C)$

$n(M \cap P \cap C)=180-120-90-70+40+30+50=20$

Therefore, the number of students who study all three subjects is 20 .

27. In a town of 10,000 families it was found that $40 \%$ families buy newspaper $\mathrm{A}, 20 \%$ families buy newspaper $\mathrm{B}, 10 \%$ families buy newspaper $\mathrm{C}, 5 \%$ families buy $\mathrm{A}$ and $\mathrm{B}, 3 \%$ buy $\mathrm{B}$ and $\mathrm{C}$ and $4 \%$ buy $\mathrm{A}$ and $\mathrm{C}$. If $2 \%$ families buy all the three newspapers. Find

(a) The number of families which buy newspaper A only.

(b) The number of families which buy none of $\mathbf{A}, \mathbf{B}$ and $\mathbf{C}$.

Given:

$n(U)=10000, n(A)=40 \%, n(B)=20 \%, n(C)=10 \%, n(A \cap B)=5 \%, n(B \cap C)=3\%$, and $\mathrm{n}(\mathrm{A} \cap \mathrm{C})=4 \%, \mathrm{n}(\mathrm{A} \cap \mathrm{B} \cap \mathrm{C})=2 \%$. $\mathrm{A}, \mathrm{B}$ and $\mathrm{C}$ are set of families who reads buys newspapers $A, B$ and $C$ respectively.

To find:

(a) The number of families which buy newspaper A only.

(b) The number of families which buy none of $\mathrm{A}, \mathrm{B}$ and $\mathrm{C}$.

Ans:

(a) The number of families which buy newspaper A only is calculated as,

$=n(A)-n(A \cap B)-n(A \cap C)+n(A \cap B \cap C)$. After substituting values we get, $\%$ only $A=40-5-4+2=33 \%$. Therefore, the number of families which buy newspaper A only will be $10000 \times \dfrac{33}{100}=3300$.

(b) The number of families which buy none of $A, B$ and $C$ is calculated as, $=n(U)-n(A \cup B \cup C)$

Using the relation of three sets, we get,

$n(A \cup B \cup C)=n(A)+n(B)+n(C)-n(A \cap B)-n(B \cap C)-n(C \cap A)+n(A \cap B \cap C)$ $\%$ of $n(A \cup B \cup C)^{\prime}=100-[40+20+10-5-3-4+2]=40 \%$.

Therefore, the number of families will be $10000 \times \dfrac{40}{100}=4000$.

28. In a group of $\mathbf{5 0}$ students, the number of students studying French, English, and Sanskrit were found to be as follows:

French $=17$, English $=13$, Sanskrit $=15$, French and English $=09$, English and Sanskrit $=4$ French and Sanskrit $=5$, English, French and Sanskrit $=3$. Find the number of students who study

(i) French only

(ii) English only

(iii) Sanskrit only

(iv) English and Sanskrit

(v) French and Sanskrit but not English

(vi) French and English but not Sanskrit

(vii) At least one of three languages

(viii) None of the three languages.

Ans: Given:

$n(U)=50, n(F)=17, n(E)=13$ and $n(S)=15, n(F \cap E)=9, n(E \cap S)=4, n(F \cap S)=5$ ,$n(F \cap E \cap S)=3 .$

Where, $\mathrm{F}, \mathrm{E}$ and $\mathrm{S}$ be the set of students who study French, English and Sanskrit respectively.

Let us consider that $\mathrm{F}, \mathrm{E}$ and $\mathrm{S}$ bet the sets which represent the number of students who study French, English and Sanskrit.

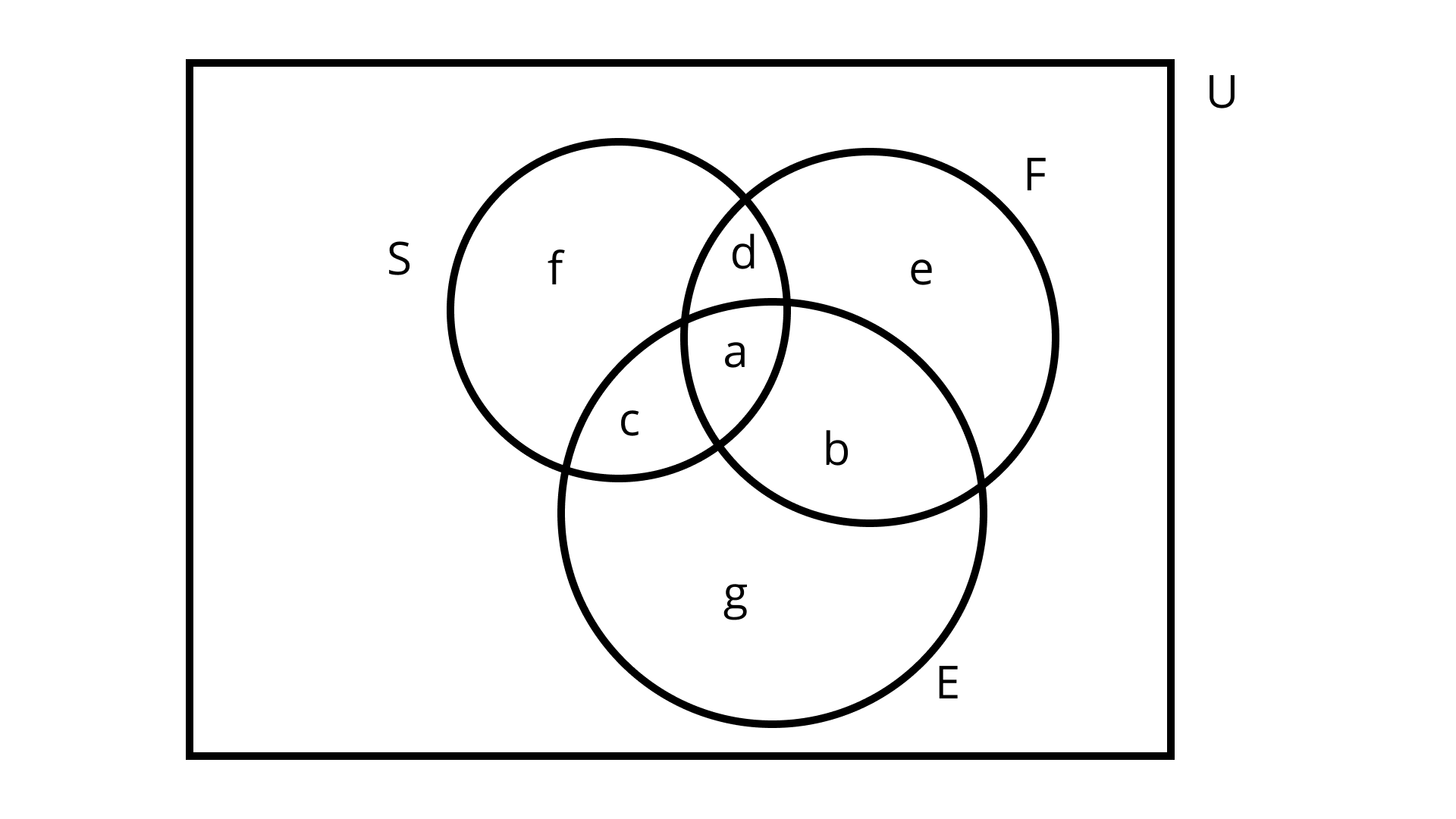
From Venn diagram assigning given values,

$n(E \cap F \cap S)=a=3, n(F \cap S)=a+d=5, n(F \cap E)=a+b=9, n(S \cap E)=a+c=4$ Some more values are, $n(F)=a+b+d+e=17, n(E)=a+b+c+g=13, n(S)=a+c+d+f=15$ From above relations we get, $a=3, b=6, c=1, d=2, e=6, f=3, g=9$. 

(i) Number of students who study French only is $\mathrm{e}=6$.

(ii) Number of students who study English only is $g=3$.

(iii) Number of students who study Sanskrit only is $f=9$.

(iv) Number of students who study English and Sanskrit but not French is $\mathrm{c}=1$.

(v) Number of students who study French and Sanskrit but not English is $d=2$.

(vi) Number of students who study French and English but not Sanskrit is $\mathrm{b}=6$.

(vii) Number of students who study at least one of three languages is $a+b+c+d+e+f+g=30$

(viii) Number of student who study none of the three languages is $=n(U)-(a+b+c+d+e+f+g) \Leftrightarrow 50-30=20 .$

Objective Type Questions

Choose the Correct Answers from the given four Options in each Exercises 29 to 43

(M.C.Q.)

29. Suppose, $A_{1}, A_{2}, \ldots \ldots A_{30}$ are thirty sets each having 5 elements and $B_{1}, B_{2}, \ldots . B_{n}$ are $n$ sets each with three elements, let $\bigcup_{i=1}^{30} A_{i}=\bigcup_{j=1}^{n} B_{j}=S$ and each element of $S$ belongs to exactly 10 of the $A_{1}$ 's and exactly 9 of $B_{j}$ 's. Then, $n$ is equal to

(A) 15

(B) 3

(C) 45

(D) 35

Ans: Correct answer is option C.

Given: $A_{1}, A_{2}, \ldots . . A_{30}$ are thirty sets with 5 elements and $B_{1}, B_{2}, \ldots . B_{n}$ are $n$ sets each with three elements.

A relation,

$\bigcup_{i=1}^{30} A_{i}=\bigcup_{j=1}^{n} B_{j}=S$

To find: $\mathrm{n}=?$

If elements are not repeated, then number of elements in $\mathrm{A}_{1} \cup \mathrm{A}_{2} \cup \mathrm{A}_{3} \ldots . . . \cup \mathrm{A}_{30}$ is $30 \times 5$.

But each element is used 10 times, so $S=\dfrac{30 \times 5}{10}$

$S=15$

If elements in $\mathrm{B}_{1}, \mathrm{~B}_{2}, \ldots . \mathrm{B}_{\mathrm{n}}$ are not repeated, then total number of elements in $3 \mathrm{n}$ but each element is repeated 9 times, so

$\Rightarrow \mathrm{S}=\dfrac{3 \mathrm{n}}{9}$

$\Rightarrow 15=\dfrac{3 \mathrm{n}}{9}$

$\Rightarrow \mathrm{n}=45 .$

30. Two finite sets have $m$ and $n$ elements. The number of subsets of the first set is 112 more than that of the second set. The values of $m$ and $n$ are, respectively

(A) 4,7

(B) 7,4

(C) 4,4

(D) 7,7

Ans: Correct answer is option A.

Given: Two finite sets with $m$ and $n$ elements.

To find: The values of $m$ and $n$ are

$\mathrm{m}=?$

$\mathrm{n}=?$

Since, the number of subsets of a containing $m$ elements is 112 more than the subsets of the set containing $\mathrm{n}$ elements.

$\Rightarrow 2^{\mathrm{m}}-2^{\mathrm{n}}=112$

$\Rightarrow 2^{\mathrm{n}}\left(2^{\mathrm{m-n}}-1\right)=2^{4} \cdot 7$

$\Rightarrow 2^{\mathrm{n}}=4$ and $2^{\mathrm{m-n}}-1=7$

$\Rightarrow \mathrm{n}=4$ and $2^{\mathrm{m-n}}=8$

$\Rightarrow \mathrm{n}=4$ and $2^{\mathrm{m-n}}=2^{3}$

$\Rightarrow m-n=3$ and $n=4$

$\Rightarrow \mathrm{m}=7$ and $\mathrm{n}=4$

31. The set $(A \cap B^{\prime})^{\prime} \cup (B \cap C)$ is equal to 

(A) $A^{\prime} \cup B \cup C$

(B) $A^{\prime} \cup B$

(C) $A^{\prime} \cup C^{\prime}$

(D) $A^{\prime} \cap B$

Ans: Correct answer is option B.

To find: $\left(A \cap B^{\prime}\right)^{\prime} \cup(B \cap C)=$ ?

We know that,

$(A \cap B)^{\prime}=\left(A^{\prime} \cup B^{\prime}\right) \text { and }\left(A^{\prime}\right)^{\prime}=A$

$=\left(A \cap B^{\prime}\right)^{\prime} \cup(B \cap C)$

$=\left[\left(A^{\prime} \cup\left(B^{\prime}\right)^{\prime}\right] \cup(B \cap C)\right.$

$=\left(A^{\prime} \cup B\right) \cup(B \cap C)$

$=A^{\prime} \cup B$

32. Let $F_{1}$ be the set of parallelograms, $F_{2}$ the set of rectangles, $F_{3}$ the set of rhombuses, $F_{4}$ the set of squares and $\mathrm{F}_{5}$ the set of trapezium in the plane. Then, $\mathrm{F}_{1}$ may be equal to

(A) $\mathrm{F}_{2} \cap \mathrm{F}_{3}$

(B) $F_{3} \cap F_{4}$

(C) $\mathrm{F}_{2} \cup \mathrm{F}_{5}$

(D) $\mathrm{F}_{2} \cup \mathrm{F}_{3} \cup \mathrm{F}_{4} \cup \mathrm{F}_{1}$

Ans: Correct option is option D.

Given: $\mathrm{F}_{1}, \mathrm{~F}_{2}, \mathrm{~F}_{3}, \mathrm{~F}_{4}$ and $\mathrm{F}_{5}$

To find: $\mathrm{F}_{1}=?$

Since square, rectangles and rhombus all are parallelograms but trapezium is not a parallelogram as a parallelogram has two pairs of parallel sides while trapezium has only one pair of parallel sides.

So, $\mathrm{F}_{1}$ is either of $\mathrm{F}_{1}, \mathrm{~F}_{2}, \mathrm{~F}_{3}$ and $\mathrm{F}_{4}$.

$\Rightarrow \mathrm{F}_{1}=\mathrm{F}_{2} \cup \mathrm{F}_{3} \cup \mathrm{F}_{4} \cup \mathrm{F}_{1}$

33. Let $\mathbf{S}=$ set of points inside the square, $\mathbf{T}=$ set of points inside the triangle and $\mathbf{C}=$ set of points inside the circle. If the triangle and circle intersect each other and are contained in a square Then,

(A) $S \cap T  \cap C=\Phi$

(B) $S \cup T \cup C=C$

(C) $\mathrm{S} \cup \mathrm{T} \cup \mathrm{C}=\mathrm{S}$

(D) $S \cup T=S \cap C$

Ans: Correct answer is option (C).

Given: $\mathrm{S}, \mathrm{T}, \mathrm{C}$ are a set of points inside square, Triangle and circle.

To find: The relation between the sets $\mathrm{S}, \mathrm{T}$, and $\mathrm{C}$.

The given sets can be represented in Venn diagram as show below,

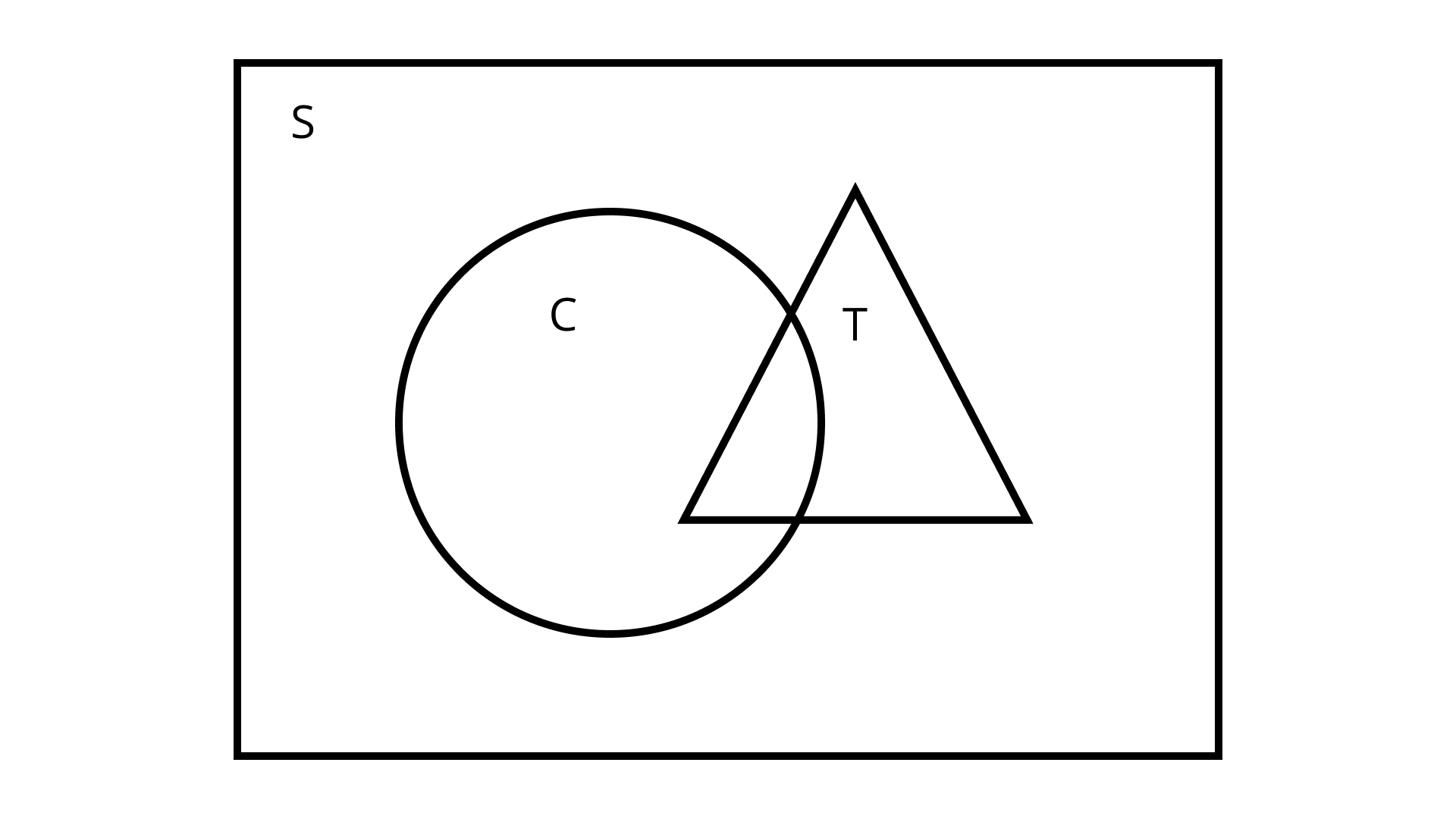
It is clear from the diagram that, $\mathrm{S} \cup \mathrm{T} \cup \mathrm{C}=\mathrm{S}$.

34. If $R$ be the set of points inside a rectangle of sides $a$ and $b(a, b>1)$ with two sides along the positive direction of $\mathbf{x}$ - axis and $\mathbf{y}$ - axis. Then,

(A) $R=\{(x, y) : 0 \leq x \leq a, 0 \leq y \leq b\}$

(B) $R=\{(x, y) : 0 \leq x<a, 0 \leq y \leq b\}$

(C) $R=\{(x, y) : 0 \leq x \leq a, 0< y< b\}$

(D) $R=\{(x, y): 0<x<a, 0<y<b\}$

Ans: Correct answer is option D

Given: $R$ as a set of points inside a rectangle.

To find: Set $\mathrm{R}=$ ?

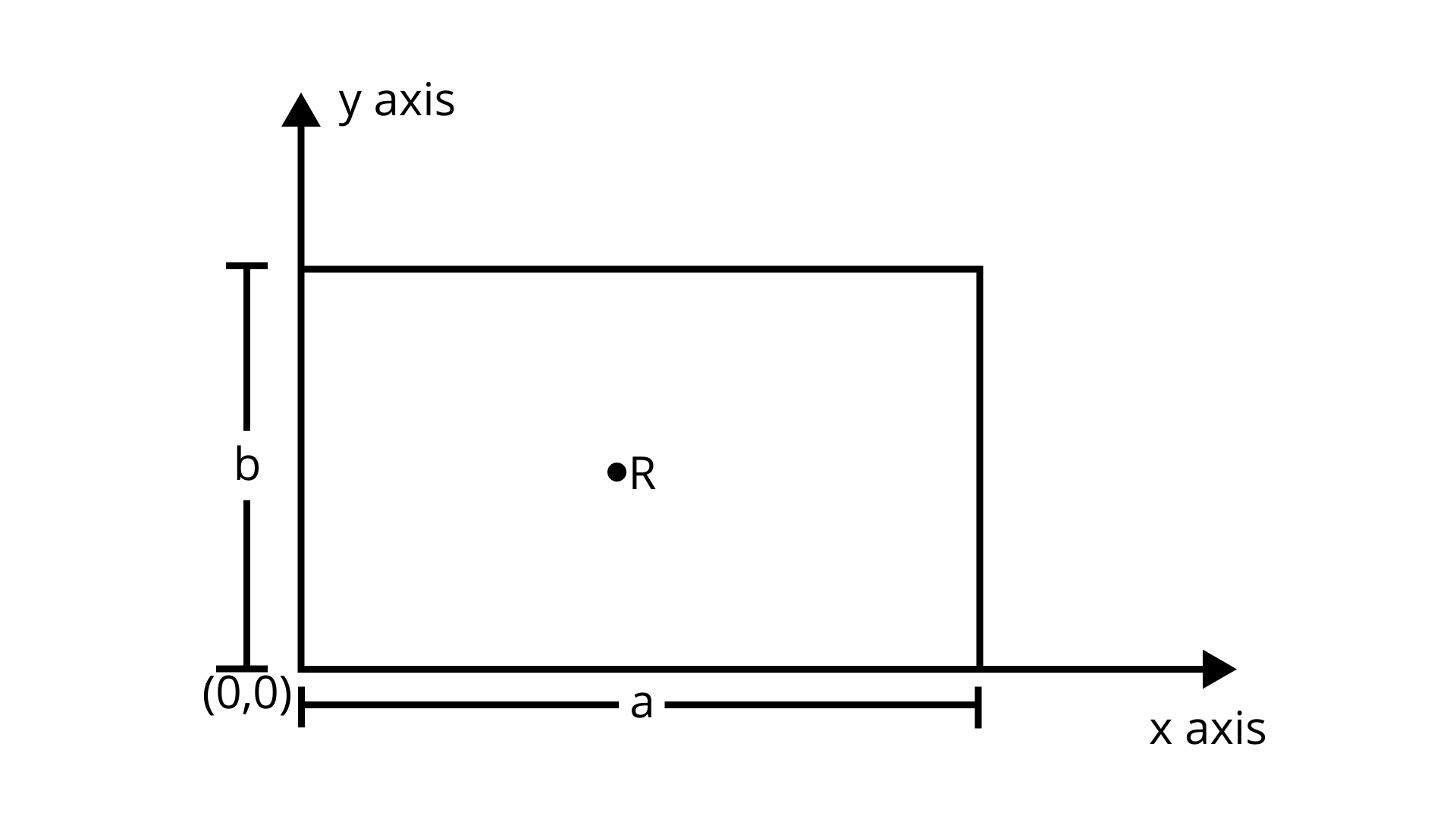
As, $R$ be the set of points inside the rectangle.

Under the given conditions, $R=\{(x, y): 0<x<a, 0<y<b\}$.

35. In a class of 60 students, 25 students play cricket and 20 students play tennis, and 10 students play both the games. Then, the number of students who play neither is

(A) 0

(B) 25

(C) 35

(D) 45

Ans: Correct answer is option B.

Given: $n(U)=60, n(C)=25, n(T)=20$ and $n(C \cap T)=10$.

To find: number of students who play neither cricket or tennis $=n(C \cup T)^{\prime}=?$

Let, $C$ be the set of students who play cricket and $T$ be the set of students who play tennis. Now, using important results of two sets, substitute the values in the formula, 

Now, remove the number of students who play cricket or tennis from the universal set that is the total number of students in class.

$n(C \cup T)=n(C)+n(T)-n(C\cap T) \Rightarrow n(C\cup T)=25+20-10=35$

The number of students who play neither is $n(C \cup T)^{\prime}=n(U)-n(C \cup T)=60-35=25$.

36. In a town of 840 persons, 450 persons read Hindi, 300 read English and 200 read both. Then, the number of person who read neither, is

(A) 210

(B) 290

(C) 180

(D) 260

Ans: Correct answer is option B.

Given: $\mathrm{n}(\mathrm{U})=840, \mathrm{n}(\mathrm{H})=450, \mathrm{n}(\mathrm{E})=300, \mathrm{n}(\mathrm{H} \cap \mathrm{E})=200$.

To find: $\mathrm{n}\left(\mathrm{H}^{\prime} \cap \mathrm{E}^{\prime}\right)=?$

$n\left(H^{\prime} \cap E^{\prime}\right)=n(H \cup E)^{\prime}$

$\Rightarrow n(H \cup E)^{\prime}=n(U)-n(H \cup E)$

$\Rightarrow n(H \cup E)^{\prime}=n(U)-[n(H)+n(E)-n(H \cap E)]$

$\Rightarrow n(H \cup E)^{\prime}=840-(450+300-200)$

$\Rightarrow n\left(H^{\prime} \cap E^{\prime}\right)=290$

37. If $X=\left\{8^n-7n-1 \mid n \in N\right\}.$ and $Y=\{49 n-49 \mid n \in N\}$ Then,

(A) $\mathrm{X} \subset \mathrm{Y}$

(B) $Y \subset X$

(C) $\mathbf{X}=\mathbf{Y}$

(D) $X \cap Y=f$

Ans: Correct answer is option A.

Given:

$X=\left\{8^{n}-7 n-1 \mid n \in N\right\}$

$Y=\{49 n-49 \mid n \in N\}$

To find: Relation between $\mathrm{X}$ and $\mathrm{Y}$.

$X=\{0,49,490, \ldots . .\}$

$Y=\{0,49,98,147, \ldots \ldots . .\}$

Every element of $\mathrm{X}$ is in $\mathrm{Y}$ but every element of $\mathrm{Y}$ is not in $\mathrm{X}$.

Therefore, $\mathrm{X} \subset \mathrm{Y}$.

38. A survey shows that $63 \%$ of the people watch a news channel whereas $76 \%$ watch another channel. If $\mathbf{x} \%$ of the people watch both channel, then

(A) $x=35$

(B) $x=63$

(C) $39 \leq x \leq 63$

(D) $x=39$

Ans: Correct answer is option C

Given: $n(A)=63, n(B)=76$ and $n(A \cap B)=x$.

To find: $x=?$

$\text { Let } n(A \cup B) \leq 100$

$\Rightarrow n(A)+n(B)-n(A \cap B) \leq 100$

$\Rightarrow 63+76-x \leq 100$

$\Rightarrow 39 \leq x$

$\because n(A)=63$

$\Rightarrow n(A \cap B) \leq n(A)$

$\Rightarrow x \leq 63$

$\therefore 39 \leq x \leq 63$

39. If sets $A$ and $B$ are defined as

$A=\left\{(x, y) \mid y=\dfrac{1}{x}, 0 \neq x \in R\right\},$

$B=\{(x, y) \mid y=-x, x \in R\}$.  Then,

(A) $A \cap B=A$

(B) $A \cap B=B$

(C) $A \cap B=\phi$

(D) $A \cup B=A$

Ans: Correct answer is option C.

Given:

$A=\left\{(x, y) \mid y=\dfrac{1}{x}, 0 \neq x \in R\right\},$

$B=\{(x, y) \mid y=-x, x \in R\}$ .

To find: Relation between sets A and B.

Let $x \in R$,

Here,

$-x \neq \dfrac{1}{x}$

$\therefore A \cap B=\phi $.

40. If $A$ and $B$ are two sets, then $A \cap (A \cup B)$ equals to:

(A) $\mathbf{A}$

(B) $\mathrm{B}$

(C) $\phi$

(D) $A \cap B$

Ans: Correct answer is option A.

Given: $A$ and $B$ are two sets.

To find: $A \cap(A \cup B)=$ ?

$\mathrm{A} \cap(A \cup B)$

$=(A \cap A)\cup(A \cap B) (\mathrm{De} \text { Morgan's Law })$

$=\left(\mathrm{A} \cap \mathrm{A}\right) \cup\left(\mathrm{A} \cap \mathrm{B}\right)$

$=\mathrm{A} \cup\left(\mathrm{A} \cap \mathrm{B}\right)$

$= A$

$\therefore \mathrm{A} \cap(\mathrm{A} \cup \mathrm{B})=\mathrm{A}$

41. If $A=\{1,3,5,7,9,11,13,15,17\}, B=\{2,4, \ldots . .18\}$ and $N$ the set of natural numbers is the universal set, then $\left(A^{\prime} \cup(A \cup B) \cap B^{\prime}\right)$ is

(A) $\phi$

(B) $\mathbf{N}$

(C) $\mathbf{A}$

(D) $\mathrm{B}$

Ans: Correct answer is option B. 

Given:

$A=\{1,3,5,7,9,11,13,15,17\}$,

$B=\{2,4, \ldots . .18\}$ and $N$.

To find: $\left(A^{\prime} \cup(A \cup B) \cap B^{\prime}\right)=?$

We have,

$\left(A^{\prime} \cup(A \cup B) \cap B^{\prime}\right)$

$=A^{\prime} \cup\left[\left(A \cap B^{\prime}\right) \cup\left(B \cap B^{\prime}\right)\right]$

$=A^{\prime} \cup\left[\left(A \cap B^{\prime}\right) \cup \phi\right]$

$=\left(A^{\prime} \cup A\right) \cap\left(A^{\prime} \cup B^{\prime}\right)$

$=N \cap\left(A^{\prime} \cup B^{\prime}\right)$ ∵$ A\cup A^{\prime}=N$

$=A^{\prime} \cup B^{\prime}$ 

$=(A \cap B)^{\prime}={\phi}^{\prime}$

$=\mathrm{N}$ 

42. If $S=\{x \mid x$ is a positive multiple of 3 less than 100$\}$ and $P=\{x \mid x$ is a prime number less than 20$\} .$ Then, $\mathbf{n}(\mathbf{S})+\mathbf{n}(\mathbf{P})$ is equal to

(A) 34

(B) 31

(C) 33

(D) 41

Ans: Correct answer is option D.

Given:

$\mathrm{S}=\{\mathrm{x} \mid \mathrm{x}$ is a positive multiple of 3 less than 100$\}$,

$P=\{x \mid x$ is a prime number less than 20$\}$.

To find: $n(S)+n(P)=?$

Clearly,

$n(S)=33$ and $n(P)=8$

$\therefore \mathrm{n}(\mathrm{S})+\mathrm{n}(\mathrm{P})=33+8$

$\Rightarrow \mathrm{n}(\mathrm{S})+\mathrm{n}(\mathrm{P})=41$.

43. If $X$ and $Y$ are two sets and $X^{\prime}$ denotes the complement of $X$, then $X \cap (X U Y)^{\prime}$  is equal to

(A) $\mathbf{X}$

(B) $\mathbf{Y}$

(C) $\phi$

(D) $X \cap Y$

Ans: Correct answer is option (C). 

Given: $\mathrm{X}$ and $\mathrm{Y}$ are sets.

To find: $X \cap(X \cup Y)^{\prime}=?$

Since $(A\cap B)^{\prime}=A^{\prime} \cup B^{\prime}$

So, $X \cap(X \cup Y)^{\prime}$

$=X \cap(X^{\prime} \cap Y^{\prime})$

$=X \cap(X^{\prime} \cap Y^{\prime})$

$=(X \cap X^{\prime})\cap(X \cap Y^{\prime})$

$=\phi \cap(X \cap Y^{\prime})$ ∵$ A\cap A^{\prime}=\phi \text{ and } \phi \cap A=\phi$

$=\phi $

Fill in the Blanks in each of the Exercises from 44 to 51 : 

44. The set $\{x \in R: 1 \leq x<2\}$ can be written as ........

Ans: Since, only 1 is included in the set. The set $\{x \in R: 1 \leq x<2\}$ can be written as $\{1\}$.

45. When $A=\phi$, then the number of elements in $P(A)$ is.......

Given: $\mathrm{A}=\phi$.

To find: $n[P(A)]=?$

Ans: Here, $\mathrm{A}=\phi$

$\Rightarrow \mathrm{n}(\mathrm{A})=0$

Now, $n[P(A)]=2^{n(A)}$

$\Rightarrow \mathrm{n}[\mathrm{P}(\mathrm{A})]=2^{0}$

$\therefore \mathrm{n}[\mathrm{P}(\mathrm{A})]=1$.

46. If $\mathbf{A}$ and $\mathbf{B}$ are finite sets, such that $\mathbf{A} \subset \mathbf{B}$, then $\mathbf{n} \left(\mathbf{A} \cup \mathbf{B}\right)$ is equal to ......... 

Given: $\mathrm{A}$ and $\mathrm{B}$ are finite sets and $\mathrm{A} \subset \mathrm{B}$.

To find:

Ans: Here, $A \subset B$

$\Rightarrow \mathrm{n}(\mathrm{A} \cap \mathrm{B})=\mathrm{n}(\mathrm{A})$

$n(A \cup B)=n(A)+n(B)-n(A \cap B)$

$n(A \cup B)=n(A)+n(B)-n(A)$

$\therefore \mathrm{n}(\mathrm{A} \cup \mathrm{B})=\mathrm{n}(\mathrm{B})$.

47. If $\mathbf{A}$ and $\mathbf{B}$ are any two sets, then $\mathbf{A}-\mathbf{B}$ is equal to ......

Given: $A$ and $B$ are two sets.

To find: $\mathrm{A}-\mathrm{B}=$ ?

Ans: 

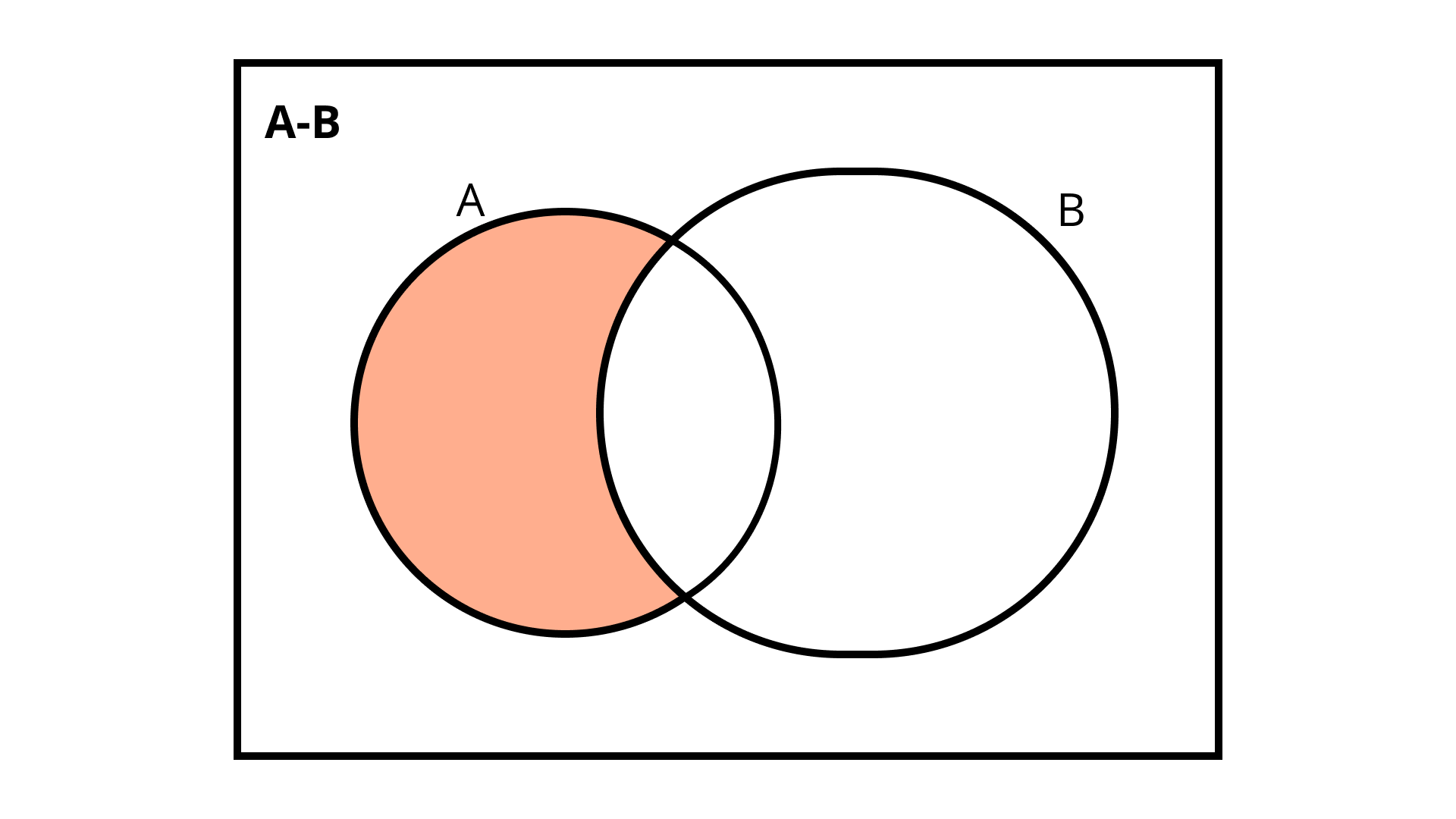
$A-B=A \cap B^{\prime}$.

48. Power set of the set $\mathbf{A}=\{1,2\}$ is ......

Given: $A=\{1,2\}$.

To find: $\mathrm{P}(\mathrm{A})=$ ?

Ans:

Here, $A=\{1,2\}$

Subsets of $\mathrm{A}$ are $\phi,\{1\},\{2\}$ and $\{1,2\}$.

$\therefore \mathrm{P}(\mathrm{A})=\{\phi,\{1\},\{2\},\{1,2\}\} .$

49. If set $A=\{1,3,5\}, B=\{2,4,6\}$ and $C=\{0,2,4,6,8\}$. Then the universal set of all the three sets $\mathrm{A}, \mathrm{B}$ and $\mathrm{C}$ can be ......

Explanation:

Given: $A=\{1,3,5\}, B=\{2,4,6\}$ and $C=\{0,2,4,6,8\}$.

To find: $U=?$

Ans:

Combination of all the three sets $\mathrm{A}, \mathrm{B}$ and $\mathrm{C}$ such that all the three sets are subsets of a universal set will form a universal set.

Therefore, universal set for $\mathrm{A}, \mathrm{B}$ and $\mathrm{C}$ can be given by $\mathrm{U}=\{0,1,2,3,4,5,6,8\}$.

50. If $\mathrm{U}=\{1,2,3,4,5,6,7,8,9,10\}, \mathrm{A}=\{1,2,3,5\}, \mathrm{B}=\{2,4,6,7\}$ and $\mathrm{C}=\{2,3,4,8\}$. Then,

 (i) $(B \cup C)^{\prime}$ is ......

Given:

$\mathrm{U}=\{1,2,3,4,5,6,7,8,9,10\}$

$\mathrm{A}=\{1,2,3,5\},$

$\mathrm{B}=\{2,4,6,7\} \text { and } \mathrm{C}=\{2,3,4,8\}$ .

Here,

$(B \cup C)=\{2,3,4,6,7,8\}$

$\Rightarrow(B \cup C)^{\prime}=U-(B \cup C)$

$\Rightarrow(B \cup C)^{\prime}=\{1,2,3,4,5,6,7,8,9,10\}-\{2,3,4,6,7,8\}$

$\therefore(B \cup C)=\{1,5,9,10\}$

(ii) $(\mathbf{C}-\mathbf{A})^{\prime}$ is $\ldots . . .$

Ans: Here,

$(C-A)=\{2,3,4,8\}-\{1,2,3,5\}$

$\Rightarrow (C-A)=\{4,8\}$

$\Rightarrow (C-A)^{\prime}=U-(C-A)$

$\Rightarrow (C-A)^{\prime}=\{1,2,3,4,5,6,7,8,9,10\}-\{4,8\}$

$\therefore(C-A)^{\prime}=\{1,2,3,5,6,7,9,10\}$ .

51. For all sets $A$ and $B, A-\left(A \cap B \right).$ is equal to .........

Given: $\mathrm{A}$ and $\mathrm{B}$ are sets.

To find: $A-(A \cap B)=?$

Ans: Here,

$A-(A \cap B)=A \cap(A \cap B)^{\prime} \quad\left\{A s,(A-B)=\left(A \cap B^{\prime}\right)\right\}$

$\Rightarrow A-(A \cap B)=A \cap\left(A^{\prime} \cup B^{\prime}\right) \quad\left\{A s,(A \cap B)^{\prime}=\left(A^{\prime} \cup B^{\prime}\right)\right\}$

$\Rightarrow A-(A \cap B)=\left(A \cap A^{\prime}\right) \cup\left(A \cap B^{\prime}\right)$

$\Rightarrow A-(A \cap B)=\phi \cup\left(A \cap B^{\prime}\right)$

$\Rightarrow A-(A \cap B)=A \cap B^{\prime}$ .

52. Match the following sets for all sets $A, B$ and $C$.

Given: $A, B$ and $C$ are sets.

To find: Correct matches.

Ans:

(i) Here,

$\left(\left(A^{\prime} \cup B^{\prime}\right)-A\right)^{\prime}=\left[\left(A^{\prime} \cup B^{\prime}\right) \cap A^{\prime}\right]^{\prime}$

$\Rightarrow \left(\left(A^{\prime} \cup B^{\prime}\right)-A\right)^{\prime}=\left[(A \cap B)^{\prime} \cap A^{\prime}\right]^{\prime}$

$\Rightarrow \left(\left(A^{\prime} \cup B^{\prime}\right)-A\right)^{\prime}=\left[(A \cap B)^{\prime}\right]^{\prime} \cup\left(A^{\prime}\right)^{\prime}$

$\Rightarrow \left(\left(A^{\prime} \cup B^{\prime}\right)-A\right)^{\prime}=(A \cap B) \cup A$

$\Rightarrow \left(\left(A^{\prime} \cup B^{\prime}\right)-A\right)^{\prime}=A$

Therefore, $\leftrightarrow$ (b)

(ii) Here,

${\left[B^{\prime} \cup\left(B^{\prime}-A\right)\right]^{\prime}=\left[B^{\prime} \cup\left(B^{\prime} \cap A^{\prime}\right)\right]^{\prime}}$

$\Rightarrow {\left[B^{\prime} \cup\left(B^{\prime}-A\right)\right]^{\prime}=\left[B^{\prime} \cup(B \cup A)^{\prime}\right]^{\prime}}$

$\Rightarrow {\left[B^{\prime} \cup\left(B^{\prime}-A\right)\right]^{\prime}=\left(B^{\prime}\right)^{\prime} \cap\left[(B \cup A)^{\prime}\right]^{\prime}}$

$\Rightarrow {\left[B^{\prime} \cup\left(B^{\prime}-A\right)\right]^{\prime}=B \cap(B \cup A)}$

$\Rightarrow {\left[B^{\prime} \cup\left(B^{\prime}-A\right)\right]^{\prime}=B}$

Therefore, $\leftrightarrow$ ©

(iii) Here,

$(A-B)-(B-C)=\left(A \cap B^{\prime}\right)-\left(B \cap C^{\prime}\right)$

$\Rightarrow (A-B)-(B-C)=\left(A \cap B^{\prime}\right) \cap\left(B \cap C^{\prime}\right)^{\prime}$

$\Rightarrow (A-B)-(B-C)=\left(A \cap B^{\prime}\right) \cap\left[\left(B^{\prime} \cup\left(C^{\prime}\right)^{\prime}\right)\right.$

$\Rightarrow (A-B)-(B-C)=\left(A \cap B^{\prime}\right) \cap\left(B^{\prime} \cup C\right)$

$\Rightarrow (A-B)-(B-C)=\left[( A \cap ( B ^ { \prime } \cup C ) ] \cap \left[\left(B^{\prime} \cup\left(B^{\prime} \cap C\right)\right]\right.\right.$

$\Rightarrow (A-B)-(B-C)=\left[A \cap\left(B^{\prime} \cup C\right)\right] \cap B^{\prime}$

$\Rightarrow (A-B)-(B-C)=\left(A \cap B^{\prime}\right) \cap\left[\left(B^{\prime} \cup C\right) \cap B^{\prime}\right]$

$\Rightarrow (A-B)-(B-C)=\left(A \cap B^{\prime}\right) \cap B^{\prime}$

$\Rightarrow (A-B)-(B-C)=\left(A \cap B^{\prime}\right)$

$\Rightarrow (A-B)-(B-C)=A-B$

Therefore, $\leftrightarrow$ (a)

(iv) Here,

$(A-B) \cap(C-B)=\left(A \cap B^{\prime}\right) \cap\left(C \cap B^{\prime}\right)$

$\Rightarrow (A-B) \cap(C-B)=(A \cap C) \cap B^{\prime}$

$\Rightarrow (A-B) \cap(C-B)=(A \cap C)-B$

Therefore, $\leftrightarrow(f)$

(v) Here,

$A \times(B \cap C)=(A \times B) \cap(A \times C)$

Therefore, $\leftrightarrow$ (d)

(vi) Here,

$A \times(B \cup C)=(A \times B) \cup(A \times C)$

Therefore, $\leftrightarrow$ (e)

State True or False for the Following Statements in each of the Exercises from 53 to 58 :

53. If $\mathrm{A}$ is any set, then $\mathrm{A} \subset \mathrm{A}$

Ans: Every set is the subset of itself. Every element of a set $A$ is in itself a set $A$. Hence, for any set $A, A \subset A$.

Therefore, true.

54. If $M=\{1,2,3,4,5,6,7,8,9\}$ and $B=\{1,2,3,4,5,6,7,8,9\}$, then $B \not\subset M .$

Given:

$M=\{1,2,3,4,5,6,7,8,9\}$,

$B=\{1,2,3,4,5,6,7,8,9\} .$

To find: True or False.

Ans: Here, every element of set $B$ is the element of set $M$. So, set $B \subset M$.

Therefore, false.

55. The sets $\{1,2,3,4\}$ and $\{3,4,5,6\}$ are equal.

Given: $\{1,2,3,4\}$ and $\{3,4,5,6\}$ are equal sets.

To find: True or false.

Ans: Both sets $A=\{1,2,3,4\}$ and $B=\{3,4,5,6\}$ have the same number of elements.

But $2 \in A$ and $2 \notin B$.

So, $\{1,2,3,4\} \neq\{3,4,5,6\}$.

Therefore, false.

56. $Q \cup Z=Q$, where $Q$ is the set of rational numbers and $Z$ is the set of integers.

Ans: Since, every integer is also considered a rational number. Therefore, every element of $Z$ is also the element of $Q$.

So, $Q \cup Z=Q$.

Therefore, true. 

57. Let sets $\mathrm{R}$ and $\mathrm{T}$ be defined as

$\mathrm{R}=\{\mathrm{x} \in \mathrm{Z} \mid \mathrm{x}$ is divisible by 2$\}$,

$\mathrm{T}=\{\mathrm{x} \in \mathrm{X} \mid \mathrm{x}$ is divisible by 6$\} .$

Then, $\mathrm{T} \subset \mathrm{R}$.

Given:

$\mathrm{R}=\{\mathrm{x} \in \mathrm{Z} \mid \mathrm{x}$ is divisible by 2$\}$,

$\mathrm{T}=\{\mathrm{x} \in \mathrm{X} \mid \mathrm{x}$ is divisible by 6$\} .$

To find: True or False.

Ans: $\mathrm{R}=\{\ldots \ldots,-6,-4,-2,0,2,4,6, \ldots \ldots . .\}$

$\mathrm{T}=\{\ldots \ldots .,-12,-6,0,6,12, \ldots \ldots \ldots \ldots . .$

Since, every element of $\mathrm{T}$ is also the element in $\mathrm{R}$. This implies that $\mathrm{T} \subset \mathrm{R}$.

Therefore, true.

58. Given $A=\{0,1,2\}, B=\left\{x \in R \mid 0 \leq x \leq 2 \right\}.$ Then $A=B$.

Given:

$A=\{0,1,2\}$

$B=\{x \in R \mid 0 \leq x \leq 2\}$

To find: True or False.

Ans: Here, $A=\{0,1,2\}$,

Number of elements is $\mathrm{n}(\mathrm{A})=3$.

There are an infinite number of elements between 0 and 2 in $B=\{x \in R \mid 0 \leq x \leq 2\}$.

This implies that $A \neq B$.

Therefore, false.

Importance of NCERT Exemplar Class 11 Chapter 1 Solutions

NCERT exemplar for Class 11 Maths Chapter 1 - Sets are provided by the Vedantu on the official website for students to prepare and practice for the exam. The exemplar is very helpful for the preparation of the students, it helps them to understand the concepts explained in the Chapters easily. NCERT exemplar for Class 11 Chapter 1 - Sets is formulated by the expert faculty of the Vedantu as per the latest syllabus pattern advised by the Central Board of Secondary Education.

The exemplar of Chapter - 1 Sets is available in pdf form for the students so that they can use it as a reference tool to quickly review all the topics by simply downloading the pdf for further use. Students will also find the solution to every question present in their textbook, this will help them understand how to answer the conceptual questions. 

The exemplar for Class 11 of Chapter 1 - Sets will help students to prepare well and score good marks in the respective subject in the examination. The students are also advised to solve sample papers and last year’s question paper of Class 11 Maths, this will help them to understand the marking scheme as well as the question pattern. Chapter 1 Sets, focuses on the concepts of sets and operations on sets. The most important concepts are mentioned below so that the students can get an overview of the topics-

1. Sets and representation

2. Empty set 

3. Infinite and finite sets

4. Subsets 

5. Power sets

6. Equal sets

7. Intervals as subsets of R

8. Venn diagrams

9. Universal set

10. Unions of sets

11. Operation of sets

12. Complement of sets

13. Intersection sets

14. Difference of sets

15. The important formulas to solve practical problems on intersecting and union of two sets

The exemplar of Chapter 1 - sets for Class 11 has all the important questions, notes, sample papers, and last year’s questions. Students can use them to increase their marks.

Get the best solution for NCERT Exemplar Class 11 Chapter 1 in PDF format for free. Add this file to your study material and learn sets better. Understand the basic concepts of solving the problems given in the exercise of this book. Prepare yourself for the questions by using the conceptual approaches designed by the subject experts of Vedantu.