CBSE Class 11 Maths Important Questions - Chapter 2 Relations and Functions

1 Marks Questions

1. Find  $\mathbf{a}$ and $\mathbf{b}$ if $\left( \mathbf{a}-\mathbf{1},\mathbf{b}+\mathbf{5} \right)=\left( \mathbf{2,3} \right)$.

Ans. It is given that, $\left( a-1,b+5 \right)=\left( 2,3 \right)$.

Therefore, we have $a-1=2$ and $b+5=3$.

Then it implies that, $a=3$ and $b=-2$.

2. If $\mathbf{A}=\left\{ \mathbf{1},\mathbf{3},\mathbf{5} \right\}$, $\mathbf{B}=\left\{ \mathbf{2},\mathbf{3} \right\}$, then find: $\mathbf{A}\times \mathbf{B}$, (Question- 3).

Ans. Recall that if $A$ and $B$ are two non-empty sets, the Cartesian product of $A$ and $B$ is the set of all ordered pairs $\left( a,b \right)$ so that $a\in A$, $b\in B$, is represented by $A\times B$. 

Therefore, $A\times B=\left\{ \left( 1,2 \right),\left( 1,3 \right),\left( 3,2 \right),\left( 3,3 \right),\left( 5,2 \right),\left( 5,3 \right) \right\}$.

3. Find $\mathbf{B}\times \mathbf{A}$.

Ans. Since, $B\times A$ is the cartesian product set of $B$ and $A$ such that for all $b\in B$, $a\in A$, $\left( b,a \right)\in B\times A$, so we have

$B\times A=\left\{ \left( 2,1 \right),\left( 2,3 \right),\left( 2,5 \right),\left( 3,1 \right)\left( 3,3 \right),\left( 3,5 \right) \right\}$.

4. If $\mathbf{A}=\left\{ \mathbf{1,2} \right\}$, $\mathbf{B}=\left\{ \mathbf{2},\mathbf{3},\mathbf{4} \right\}$, $\mathbf{C}=\left\{ \mathbf{4,5} \right\}$, then find: $\mathbf{A}\times \left( \mathbf{B}\cap \mathbf{C} \right)$, (Question- 5).

Ans.  Note that, \[B\cap C=\left\{ 4 \right\}\].

Also, given that $A=\left\{ 1,2 \right\}$.

So, by the definition of cartesian product of sets, we have

$A\times \left( B\cap C \right)=\left\{ \left( 1,4 \right),\left( 2,4 \right) \right\}$.

5. Find $\mathbf{A}\times \left( \mathbf{B}\cup \mathbf{C} \right)$.

Ans. Given that, $A=\left\{ 1,2 \right\}$, $B=\left\{ 2,3,4 \right\}$, and $C=\left\{ 4,5 \right\}$.

Then, $B\cup C=\left\{ 2,3,4,5 \right\}$.

Therefore, by the definition of cartesian product of sets, we have

$A\times \left( B\cup C \right)=\left\{ \left( 1,2 \right),\left( 1,3 \right),\left( 1,4 \right),\left( 1,5 \right),\left( 2,2 \right),\left( 2,3 \right),\left( 2,4 \right),\left( 2,5 \right) \right\}$.

6. If $\mathbf{P}=\left\{ \mathbf{1,3} \right\}$, $\mathbf{Q}=\left\{ \mathbf{2},\mathbf{3},\mathbf{5} \right\}$, find the number of relations from $\mathbf{P}$ to $\mathbf{Q}$.

Ans. It is known that, the number of relations from a set $A$ to $B$ having $m$ and $n$ elements respectively, is ${{2}^{mn}}$.

Therefore, the number of relations from $P$ to $Q$, 

$={{2}^{2\times 3}}={{2}^{6}}=64$.

7. If $\mathbf{A}=\left\{ \mathbf{1,2,3,5} \right\}$ and $\mathbf{B}=\left\{ \mathbf{4,6,9} \right\}$, $\mathbf{R}=\left\{ \left( \mathbf{x},\mathbf{y} \right):\left| \mathbf{x}-\mathbf{y} \right|\text{ }\mathbf{is odd},\ \mathbf{x}\in \mathbf{A},\,\mathbf{y}\in \mathbf{B} \right\}$. Write $\mathbf{R}$ in roster form.

Ans. 

The roster form of the set $R$ is given by

$R=\left\{ \left( 1,4 \right),\left( 1,6 \right),\left( 2,9 \right),\left( 3,4 \right),\left( 3,6 \right),\left( 5,4 \right),\left( 5,6 \right) \right\}$.

• Are the following relations in Question 8, 9, 10 functions? Give a proper reason.

8. $\mathbf{R}=\left\{ \left( \mathbf{1,1} \right)\mathbf{,}\left( \mathbf{2,2} \right)\mathbf{,}\left( \mathbf{3,3} \right)\mathbf{,}\left( \mathbf{4,4} \right)\mathbf{,}\left( \mathbf{4,5} \right) \right\}$.

Ans. The given relation is $R=\left\{ \left( 1,1 \right),\left( 2,2 \right),\left( 3,3 \right),\left( 4,4 \right),\left( 4,5 \right) \right\}$.

Notice that, the element $4$ possesses two images, such that $\left( 4,4 \right)$ and $\left( 4,5 \right)$.

Therefore, since a function should have unique image for each element, so $R$ cannot be a function.

9. $\mathbf{R}=\left\{ \left( \mathbf{2,1} \right)\mathbf{,}\left( \mathbf{2,2} \right)\mathbf{,}\left( \mathbf{2},\mathbf{3} \right),\left( \mathbf{2},\mathbf{4} \right) \right\}$.

Ans. The given relation is $R=\left\{ \left( 2,1 \right),\left( 2,2 \right),\left( 2,3 \right),\left( 2,4 \right) \right\}$.

Observe that, for the element $2$, there are four different images such that $\left( 2,1 \right),\left( 2,2 \right),\left( 2,3 \right),$ and $\left( 2,4 \right)$.

Therefore, since a function should have unique image for each of the element, so the relation $R$ cannot be a function.

10. $\mathbf{R}=\left\{ \left( \mathbf{1,2} \right)\mathbf{,}\left( \mathbf{2,5} \right)\mathbf{,}\left( \mathbf{3,8} \right)\mathbf{,}\left( \mathbf{4,10} \right)\mathbf{,}\left( \mathbf{5,12} \right)\mathbf{,}\left( \mathbf{6,12} \right) \right\}$. 

Ans. The given relation is 

$R=\left\{ \left( 1,2 \right),\left( 2,5 \right),\left( 3,8 \right),\left( 4,10 \right),\left( 5,12 \right),\left( 6,12 \right) \right\}$.

Observe that, each of the elements in the given relation possesses a unique image.

Therefore, the relation $R$ is a function.

11. Is the following arrow diagram represent a function? Why?

Ans. Notice that, each of the elements of the set  $X=\left\{ a,b,c,d \right\}$ corresponds to a unique image of the set $Y=\left\{ 0,1,2,3,4 \right\}$.

Therefore, the relation given in the diagram is a function.

12. Is the following arrow diagram represent a function? Why?

Ans. Observe that, each of the elements of the set $X=\left\{ 2,3,5,7 \right\}$ corresponds to a unique element of the set $Y=\left\{ -1,0,2,4,3 \right\}$, except  the element $2\in X$ which corresponds to two different images such that $\left( 2,0 \right)$ and $\left( 2,3 \right)$.

Therefore, the relation given in the diagrams cannot be a function.

• Let $\mathbf{f}$ and $\mathbf{g}$ be two real valued functions, defined by, $\mathbf{f}\left( \mathbf{x} \right)={{\mathbf{x}}^{\mathbf{2}}}\mathbf{,}\,\,\mathbf{g}\left( \mathbf{x} \right)=\mathbf{3x+2}$.

13. Find the value of $\left( \mathbf{f}+\mathbf{g} \right)\left( \mathbf{-2} \right)$.

Ans. The given functions are $f\left( x \right)={{x}^{2}}$, $g\left( x \right)=3x+2$.

Therefore, $\left( f+g \right)\left( x \right)=f\left( x \right)+g\left( x \right)={{x}^{2}}+3x+2$

So, substituting $x=-2$, we obtain

$\left( f+g \right)\left( -2 \right)={{\left( -2 \right)}^{2}}+3\left( -2 \right)+2$

$ =4-6+2 $

$ =0. $

Hence, $\left( f+g \right)\left( -2 \right)=0$.

14. Find the value of $\left( \mathbf{f-g} \right)\left( \mathbf{1} \right)$.

Ans. The given functions are $f\left( x \right)={{x}^{2}}$, $g\left( x \right)=3x+2$.

Therefore, 

  $\left( f-g \right)\left( x \right)=f\left( x \right)-g\left( x \right) $

 $={{x}^{2}}-\left( 3x+2 \right) $

 $={{x}^{2}}-3x-2 $

Substituting $x=1$, we get

  $\left( f-g \right)\left( 1 \right)={{\left( 1 \right)}^{2}}-3\left( 1 \right)-2 $

 $=1-3-2 $

 $=-2-2 $

 $=-4. $

Hence, $\left( f-g \right)\left( 1 \right)=-4$.

15. Find the value of $\left( \mathbf{fg} \right)\left( \mathbf{-1} \right)$.

Ans. The given functions are $f\left( x \right)={{x}^{2}}$, $g\left( x \right)=3x+2$.

Therefore, $\left( fg \right)\left( x \right)=f\left( x \right)g\left( x \right)={{x}^{2}}\left( 3x+2 \right)$.

Substituting $x=-1$, we have

$\left( fg \right)\left( -1 \right)={{\left( -1 \right)}^{2}}\left\{ 3\left( -1 \right)+2 \right\} $

 $=-3+2 $

 $=-1. $

Hence, $\left( fg \right)\left( -1 \right)=-1$.

16. Find the value of $\left( \frac{\mathbf{f}}{\mathbf{g}} \right)\left( \mathbf{0} \right)$.

Ans. The given functions are $f\left( x \right)={{x}^{2}}$, $g\left( x \right)=3x+2$.

Then, $\left( \frac{f}{g} \right)\left( x \right)=\frac{f\left( x \right)}{g\left( x \right)}=\frac{{{x}^{2}}}{3x+2}$.

Substituting, $x=0$, we get

$\left( \frac{f}{g} \right)\left( 0 \right)=\frac{{{\left( 0 \right)}^{2}}}{3\left( 0 \right)+2}=0$.

That is, $\left( \frac{f}{g} \right)\left( 0 \right)=0$.

17. If $\mathbf{f}\left( \mathbf{x} \right)={{\mathbf{x}}^{\mathbf{3}}}$, find the value of $\frac{\mathbf{f}\left( \mathbf{5} \right)\mathbf{-f}\left( \mathbf{1} \right)}{\mathbf{5-1}}$.

Ans. It is given that,

$f\left( x \right)={{x}^{3}}$.

Substituting $x=1$ we get,

$f\left( 1 \right)={{1}^{3}}=1$ and

substituting $x=5$, we obtain

$f\left( 5 \right)={{5}^{3}}=125$.

Therefore, $\frac{\text{f}\left( \text{5} \right)\text{-f}\left( \text{1} \right)}{\text{5-1}}=\frac{125-1}{4}=\frac{124}{4}=31$.

Hence, the value of $\frac{\text{f}\left( \text{5} \right)\text{-f}\left( \text{1} \right)}{\text{5-1}}$ is $31$.

18. Find the domain of the real function, $\mathbf{f}\left( \mathbf{x} \right)=\sqrt{{{\mathbf{x}}^{\mathbf{2}}}\mathbf{-4}}$.

Ans. The given function is $f\left( x \right)=\sqrt{{{x}^{2}}-4}$.

Observe that the function exists if ${{x}^{2}}-4\ge 0$, that is, if $x\ge 2$ and $x\le -2$. Thus, the domain of the real function $f\left( x \right)$ is $\left( -\infty ,-2 \right]\cup \left[ 2,\infty  \right)$.

19. Find the domain of the function, $\mathbf{f}\left( \mathbf{x} \right)=\frac{{{\mathbf{x}}^{\mathbf{2}}}\mathbf{+2x+3}}{{{\mathbf{x}}^{\mathbf{2}}}\mathbf{-5x+6}}$. 

Ans. The given function is $\text{f}\left( \text{x} \right)=\frac{{{\text{x}}^{\text{2}}}\text{+2x+3}}{{{\text{x}}^{\text{2}}}\text{-5x+6}}$.

Now, ${{x}^{2}}-5x+6=\left( x-2 \right)\left( x-3 \right)$.

Therefore, the given function can be written as

$f\left( x \right)=\frac{{{x}^{2}}+2x+3}{\left( x-2 \right)\left( x-3 \right)}$.

So, clearly for $x=2,3$, the function will be unbounded. Therefore, $f\left( x \right)$ exists for all real numbers except at $x=2,3$.

Hence, the domain of the function $f\left( x \right)$ is $\mathbb{R}-\left\{ 2,3 \right\}$.

• Find the range of the functions in Question 20, 21.

20. $\mathbf{f}\left( \mathbf{x} \right)=\frac{\mathbf{1}}{\mathbf{1-}{{\mathbf{x}}^{\mathbf{2}}}}$

Ans. We know that, range of a function is the set of all possible function values. Observe that, $f\left( x \right)$ can have all the real values except the unbounded values $-\infty ,\infty $. 

Thus, the range of the function $f\left( x \right)$ is $\left( -\infty ,0 \right]\cup \left[ 1,\infty  \right)$.

21. $\mathbf{f}\left( \mathbf{x} \right)={{\mathbf{x}}^{\mathbf{2}}}\mathbf{+2}$.

Ans. The given function is $f\left( x \right)={{x}^{2}}+2$.

Note that, ${{x}^{2}}\ge 0$. So, ${{x}^{2}}+2\ge 2$, for all real value of $x$.

Therefore, $f\left( x \right)\ge 2$, for all real value of $x$.

Thus, the range of the function $f\left( x \right)$ is $\left[ 2,\infty  \right)$.

22. Find the domain of the relation, $\mathbf{R}=\left\{ \left( \mathbf{x,y} \right)\mathbf{:x,y}\in \mathbf{Z}\,\mathbf{,xy}=\mathbf{4} \right\}$.

Ans. The given relation is $\text{R}=\left\{ \left( \text{x,y} \right)\text{:x,y}\in \mathbb{Z}\text{,}\,\,\text{xy}=\text{4} \right\}$.

Observe that, $xy=4$ for the following pair of values of $\left( x,y \right)$.

$\left( -4,-1 \right)$, $\left( -2,-2 \right)$, $\left( -1,-4 \right)$, $\left( 1,4 \right)$, $\left( 2,2 \right)$, $\left( 4,1 \right)$.

Now, we know that the domain is the set of all $x$-values.

Therefore, the domain of the given relation $R$, that is, 

$R=\left\{ \left( -4,1 \right),\left( -2,-2 \right),\left( -1,-4 \right),\left( 1,4 \right),\left( 2,2 \right),\left( 4,1 \right) \right\}$ is given by

$\left\{ -4,-2,-1,1,2,4 \right\}$.

• Find the range of the relations in Question 23, 24.

23. $\mathbf{R}=\left\{ \left( \mathbf{a,b} \right)\mathbf{:a,b}\in \mathbf{N  and 2a+b}=\mathbf{10} \right\}$.

Ans. The pair of values of $\left( a,b \right)\in \mathbb{N}$ for which the equation $2a+b=10$ is satisfied are given by

$\left( 4,2 \right),\left( 3,4 \right),\left( 2,6 \right),$ and $\left( 1,8 \right)$.

Now, we know that range of a relation is the set of all the images.

Therefore, the range of the given relation $R$, that is, $R=\left\{ \left( 4,2 \right),\left( 3,4 \right),\left( 2,6 \right),\left( 1,8 \right) \right\}$ is given by $\left\{ 2,4,6,8 \right\}$.

24. $\mathbf{R}=\left\{ \left( \mathbf{x,}\,\,\frac{\mathbf{1}}{\mathbf{x}} \right):\ \mathbf{x}\in \mathbf{z},\ \mathbf{0}<\mathbf{x}<\mathbf{6} \right\}$.

Ans. The pair of values of $\left( x,\frac{1}{x} \right)$, for all $x\in \mathbb{Z}$, such that $0 < x < 6$ are  $\left( 1,1 \right),\left( 2,\frac{1}{2} \right),\left( 3,\frac{1}{3} \right),\left( 4,\frac{1}{4} \right),$ and $\left( 5,\frac{1}{5} \right)$.

Since, the range of a relation is the set of all images, therefore, the range of the given relation $R$ is given by $\left\{ 1,\frac{1}{2},\frac{1}{3},\frac{1}{4},\frac{1}{5} \right\}$.

25. If the ordered Pairs $\left( \mathbf{x-1,y+3} \right)$ and \[\left( \mathbf{2,x+4} \right)\] are equal, find $\mathbf{x}$ and $\mathbf{y}$.

(a) $\left( \mathbf{3,3} \right)$         

(b) $\left( \mathbf{3},\mathbf{4} \right)$              

(c) $\left( \mathbf{1,4} \right)$             

(d) $\left( \mathbf{1,0} \right)$

Ans. Given that the ordered pairs $\left( \text{x-1,y+3} \right)$ and \[\left( \text{2,x+4} \right)\] are equal.

So, we have 

$x-1=2$

$\Rightarrow x=2+1=3$.

Also, we have 

$y+3=x+4$

$\Rightarrow y=x+4-3=x+1$

$\Rightarrow y=3+1=4$ substituting $x=3$

Thus, the required ordered pair is $\left( 3,4 \right)$.

Hence, option (b) is the correct answer.

26. If $\mathbf{n}\left( \mathbf{A} \right)=\mathbf{3},\,\,\mathbf{n}\left( \mathbf{B} \right)=\mathbf{2}$, $\mathbf{A}$ and $\mathbf{B}$ are two sets, then number of relations of $\mathbf{A}\times \mathbf{B}$ have.

(a) $\mathbf{6}$

(b) $\mathbf{12}$

(c) $\mathbf{32}$

(d) $\mathbf{64}$

Ans. Given that, the number of elements in the set $A$ is $n\left( A \right)=3$ and the number of elements of the set $B$ is $n\left( B \right)=2$.

Therefore, the number of relations of $A\times B$

$={{2}^{n\left( A \right)\times n\left( B \right)}} $

$={{2}^{3\times 2}} $

$={{2}^{6}} $

$=64 $

Hence, option (d) is the correct answer.

27. Let $\mathbf{f}\left( \mathbf{x} \right)=\mathbf{-}\left| \mathbf{x} \right|$, then Range of function is

(a) $\left( \mathbf{0,}\infty  \right)$

(b) $\left( -\infty ,\infty  \right)$

(c) $\left( -\infty ,\mathbf{0} \right]$

(d) none of the above

Ans. The given function is $f\left( x \right)=-\left| x \right|<0$.

Therefore, the range of the function $f\left( x \right)$ is given by $\left( -\infty ,0 \right]$.

Hence, option (c) is the correct answer.

28. A real function $\mathbf{f}$ is defined by $\mathbf{f}\left( \mathbf{x} \right)=\mathbf{2x-5}$. Then the value of $\mathbf{f}\left( \mathbf{-3} \right)$ is
(a) $\mathbf{-11}$

(b) $\mathbf{1}$

(c) $\mathbf{0}$

(d) none of the above

Ans. The given function is $f\left( x \right)=2x-5$.

Substituting $x=-3$, we obtain

 $f\left( -3 \right)=2\left( -3 \right)-5 $

 $=-6-5 $

 $=-11. $

Hence, option (a) is the correct answer.

29. If $\mathbf{P}=\left\{ \mathbf{a,b,c} \right\}$ and $\mathbf{Q}=\left\{ \mathbf{d} \right\}$, form the sets $\mathbf{P}\times \mathbf{Q}$ and $\mathbf{Q}\times \mathbf{P}$ are these sets equal?

Ans. The cartesian product $P\times Q$ is such that

$P\times Q=\left\{ \left( a,d \right),\left( b,d \right),\left( c,d \right) \right\}$.

The cartesian product $Q\times P$ is such that

$Q\times P=\left\{ \left( d,a \right),\left( d,b \right),\left( d,c \right) \right\}$.

The elements of the two sets $P\times Q$ and $Q\times P$ are not equal, since the ordered pairs are not commutative, namely $\left( a,d \right)\ne \left( d,a \right)$.

Hence, the sets $P\times Q$ and $Q\times P$ are not equal.

30. If $\mathbf{A}$ and $\mathbf{B}$ are finite sets such that $\mathbf{n}\left( \mathbf{A} \right)=\mathbf{m}$ and $\mathbf{n}\left( \mathbf{B} \right)=\mathbf{k}$, find the number of relations from $\mathbf{A}$ to $\mathbf{B}$.

Ans. It is provided that, the number of elements in the set $A$ and $B$ is $n\left( A \right)=m$ and $n\left( B \right)=k$ respectively.

Therefore, the number of relations from the set $A$ to set $B$ is 

${{2}^{n\left( A \right)\times \text{n}\left( B \right)}}={{2}^{mk}}$.

31. Let $\mathbf{f}=\left\{ \left( \mathbf{1,1} \right)\mathbf{,}\left( \mathbf{2,3} \right)\mathbf{,}\left( \mathbf{0,-1} \right)\mathbf{,}\left( \mathbf{-1,3} \right)\mathbf{,}... \right\}$ be a function from $\mathbf{z}$ to $\mathbf{z}$ defined by $\mathbf{f}\left( \mathbf{x} \right)=\mathbf{ax}+\mathbf{b}$, for some integers $\mathbf{a}$ and $\mathbf{b}$. Determine the values of $\mathbf{a}$ and $\mathbf{b}$.

Ans. The function provided is $f\left( x \right)=ax+b$.

$\left( 1,1 \right)\in f$ implies that $f\left( 1 \right)=1$.

So, substituting $x=1$ into the function, we obtain

$a+b=1$                                       …… (i)

Again, $\left( 0,-1 \right)\in f$ implies that, $f\left( 0 \right)=-1$.

Therefore, substituting $x=0$ into the function, we get

$a\left( 0 \right)+b=-1$                              …… (ii)

Substituting the value of $b$ from the equation (ii) into the equation (i), yields

$a-1=1$

$\Rightarrow a=2$

Thus, $a=2$ and $b=-1$.

32. Express $\left\{ \left( \mathbf{x,y} \right)\mathbf{:y+2x}=\mathbf{5},\,\,\mathbf{x},\mathbf{y}\in \mathbf{w} \right\}$ as the set of ordered pairs.

Ans. The values of the ordered pairs for which the equation $y+2x=5$ is satisfied are given by $\left( 0,5 \right),\left( 1,3 \right),$ and $\left( 2,1 \right)$.

There are other values of $x,y$ for which the given equation may satisfy, but these are not whole numbers.

Thus, the set in the form of ordered pairs is given by $\left\{ \left( 0,5 \right),\left( 1,3 \right),\left( 2,1 \right) \right\}$.

33. If $\mathbf{A}=\left\{ \mathbf{1,2} \right\}$, find $\mathbf{A}\times \mathbf{A}\times \mathbf{A}$.

Ans. The given set is $A=\left\{ 1,2 \right\}$.

The cartesian product $A\times A=\left\{ \left( 1,1 \right),\left( 1,2 \right),\left( 2,1 \right),\left( 2,2 \right) \right\}$.

Therefore, the cartesian product$A\times A\times A=\left\{ \left( 1,1,1 \right),\left( 1,1,2 \right),\left( 1,2,1 \right),\left( 1,2,2 \right), \left( 2,1,1 \right),\left( 2,1,2 \right),\left( 2,2,1 \right),\left( 2,2,2 \right) \right\}$.

34. A function $\mathbf{f}$ is defined by $\mathbf{f}\left( \mathbf{x} \right)=\mathbf{2x-3}$. Find $\mathbf{f}\left( \mathbf{5} \right)$.

Ans. The given function is $f\left( x \right)=2x-3$.

Then, substituting $x=5$ into the given function, yields

$f\left( 5 \right)=2\left( 5 \right)-3 $

$=10-3 $

$=7. $

Hence, $f\left( 5 \right)=7$.

35. Let $\mathbf{f}=\left\{ \left( \mathbf{0,-5} \right)\mathbf{,}\left( \mathbf{1,-2} \right)\mathbf{,}\left( \mathbf{2,1} \right)\mathbf{,}\left( \mathbf{3,4} \right)\mathbf{,}\left( \mathbf{4,7} \right) \right\}$ be a linear function from $\mathbf{Z}$ into $\mathbf{Z}$. Find $\mathbf{f}$.

Ans.  The required function is $f\left( x \right)=3x-5$.

36. If the ordered pairs $\left( \mathbf{x}-\mathbf{2},\mathbf{2y}+\mathbf{1} \right)$ and $\left( \mathbf{y-1,x+2} \right)$ are equal, then find the values of $\mathbf{x}$ and $\mathbf{y}$.

Ans. Since, the ordered pairs $\left( x-2,2y+1 \right)$ and $\left( y-1,x+2 \right)$ are equal, so we have $x-2=y-1$ and $2y+1=x+2$. That is,

$x-y=1$                                         …… (i)

$x-2y=-1$                                    …… (ii)

Solving the equations (i) and (ii), we obtain

$x=3$, and $y=2$.

37. Let $\mathbf{A}=\left\{ \mathbf{-1,2,5,8} \right\}$, $\mathbf{B}=\left\{ \mathbf{0,1,3,6,7} \right\}$ and $\mathbf{R}$ be the relation, is one less than from $\mathbf{A}$ to $\mathbf{B}$. Then, find the domain and Range of $\mathbf{R}$.

Ans. The relation $R:A\to B$ such that $A$ is one less than $B$ is given by

$R=\left\{ \left( -1,0 \right),\left( 2,3 \right),\left( 5,6 \right) \right\}$.

Therefore, domain of the relation $R=\left\{ -1,2,5 \right\}$ and range of the relation$R=\left\{ 0,3,6 \right\}$.

38. Let $\mathbf{R}$ be a relation from $\mathbf{N}$ to $\mathbf{N}$ define by $\mathbf{R}=\left[ \left( \mathbf{a,b} \right)\mathbf{:a,b}\in \mathbf{N and}\text{ }\mathbf{a}={{\mathbf{b}}^{\mathbf{2}}} \right]$. Is the following statement true?

$\mathbf{a},\mathbf{b}\in \mathbf{R}$ implies $\left( \mathbf{b},\mathbf{a} \right)\in \mathbf{R}$.

Ans. Given statement: $a,b\in R$ implies $\left( b,a \right)\in R$.

Now, suppose $a=4$ and $b=2$ so that, $\left( 4,2 \right)\in R$ and $4={{2}^{2}}$.

Although, $2\ne {{4}^{2}}$. This implies $\left( 2,4 \right)\notin R$.

Thus, the given statement is not true.

39. Let $\mathbf{N}$ be the set of natural numbers and the relation $\mathbf{R}$ be defined in $\mathbf{N}$ by $\mathbf{R}=\left\{ \left( \mathbf{x,y} \right)\mathbf{:y}=\mathbf{2x,}\,\,\mathbf{x,y}\in \mathbf{N} \right\}$. What is the domain, co-domain and range of $\mathbf{R}$? Is this relation a function?

Ans. The given relation is $R=\left\{ \left( x,y \right):y=2x,\ x,y\in \mathbb{N} \right\}$.

The domain of the relation $R$ is the natural number set $\mathbb{N}$, co-domain of the relation $R$ is also the natural number set $\mathbb{N}$ and Range of the relation $R$is the set of even natural numbers.

The relation $R$ is a function because each natural number $x$ has a distinct image $2x$.

40. Let $\mathbf{R}=\left\{ \left( \mathbf{x},\mathbf{y} \right):\mathbf{y}=\mathbf{x}+\mathbf{1} \right\}$ and $\mathbf{y}\in \left\{ \mathbf{0},\mathbf{1},\mathbf{2},\mathbf{3},\mathbf{4},\mathbf{5} \right\}$. List the element of $\mathbf{R}$.

Ans. The given relation is $R=\left\{ \left( x,y \right):y=x+1 \right\}$.

Now, for $y\in \left\{ \text{0,1,2,3,4,5} \right\}$, the $x$-values are obtained as

$-1,\,0,\,1,\,2,\,3,$ and $4$.

Therefore, the list of the elements of the given relation is $R=\left\{ \left( -1,0 \right),\left( 0,1 \right),\left( 1,2 \right),\left( 2,3 \right),\left( 3,4 \right),\left( 4,5 \right) \right\}$.

41. Let $\mathbf{f}$ be the subset of $\mathbf{Q}\times \mathbf{Z}$ defined by $\mathbf{f}=\left\{ \left( \frac{\mathbf{m}}{\mathbf{n}},\mathbf{m} \right):\mathbf{m},\mathbf{n}\in \mathbf{Z},\mathbf{n}\ne \mathbf{0} \right\}$. Is $\mathbf{f}$ a function from $\mathbf{Q}$ to $\mathbf{Z}$? Justify your answer.

Ans. The given set is $\text{f}=\left\{ \left( \frac{\text{m}}{\text{n}}\text{,m} \right)\text{:m,n}\in \text{Z,}\,\,\text{n}\ne \text{0} \right\}$.

Let $m=1$, $n=2$, then $\left( \frac{m}{n},m \right)\in f$ implies $\left( \frac{1}{2},1 \right)\in f$.

Again, if $m=2$, $n=4$, then $\left( \frac{2}{4},2 \right)\in f$.

But, since $\frac{2}{4}=\frac{1}{2}$, so we are getting two different images for $\frac{1}{2}$.

Therefore, $f$ cannot be a function from $\mathbb{Q}$ to $\mathbb{Z}$.

42. The function $\mathbf{f}$ which maps temperature in Celsius into temperature in Fahrenheit is defined by $\mathbf{f}\left( \mathbf{c} \right)=\frac{\mathbf{9}}{\mathbf{5}}\mathbf{c+32}$. Find $\mathbf{f}\left( \mathbf{0} \right)$.

Ans. The given function is $f\left( c \right)=\frac{9}{5}c+32$.

Substituting $c=0$ into the function, we have

$f\left( 0 \right)=\frac{9}{5}\left( 0 \right)+32$

$\Rightarrow f\left( 0 \right)=32$.

43. If $\mathbf{f}\left( \mathbf{x} \right)={{\mathbf{x}}^{\mathbf{3}}}\mathbf{-}\frac{\mathbf{1}}{{{\mathbf{x}}^{\mathbf{3}}}}$, then prove that $\mathbf{f}\left( \mathbf{x} \right)\mathbf{+f}\left( \frac{\mathbf{1}}{\mathbf{x}} \right)=\mathbf{0}$.

Ans. The given function is $f\left( x \right)={{x}^{3}}-\frac{1}{{{x}^{3}}}$.

Replacing $x$ by $\frac{1}{x}$ into the given function we obtain,

$f\left( \frac{1}{x} \right)=\frac{1}{{{x}^{3}}}-{{x}^{3}}$.

Therefore, adding these two functions, we get

  $f\left( x \right)+f\left( \frac{1}{x} \right)={{x}^{3}}-\frac{1}{{{x}^{3}}}+\frac{1}{{{x}^{3}}}-{{x}^{3}} $

 $=0 $

44. If $\mathbf{A}$ and $\mathbf{B}$ are two sets containing $\mathbf{m}$ and $\mathbf{n}$ elements respectively, how many different relations can be defined from to?

Ans. The number of relations from the set $A$ to $B$ is ${{2}^{mn}}$.

4 Marks Questions

1. Let \[\mathbf{A}=\left\{ \mathbf{1},\mathbf{2},\mathbf{3},\mathbf{4} \right\},\,\mathbf{B}=\left\{ \mathbf{1},\mathbf{4},\mathbf{9},\mathbf{16},\mathbf{25} \right\}\] and $\mathbf{R}$ be a relation defined from $\mathbf{A}$ to $\mathbf{B}$ as, \[\mathbf{R}=\left\{ \left( \mathbf{x},\mathbf{y} \right):\mathbf{x}\in \mathbf{A},\,\mathbf{y}\in \mathbf{B}\text{ }\mathbf{and}\text{ }\mathbf{y}={{\mathbf{x}}^{\mathbf{2}}} \right\}\]. Then do as directed.

(a) Depict this relation using arrow diagram.

Ans. The relation \[\text{R}=\left\{ \left( \text{x,y} \right)\text{:x}\in \text{A,}\,\text{y}\in \text{B and y}={{\text{x}}^{\text{2}}} \right\}\] can be represented by the following diagram.

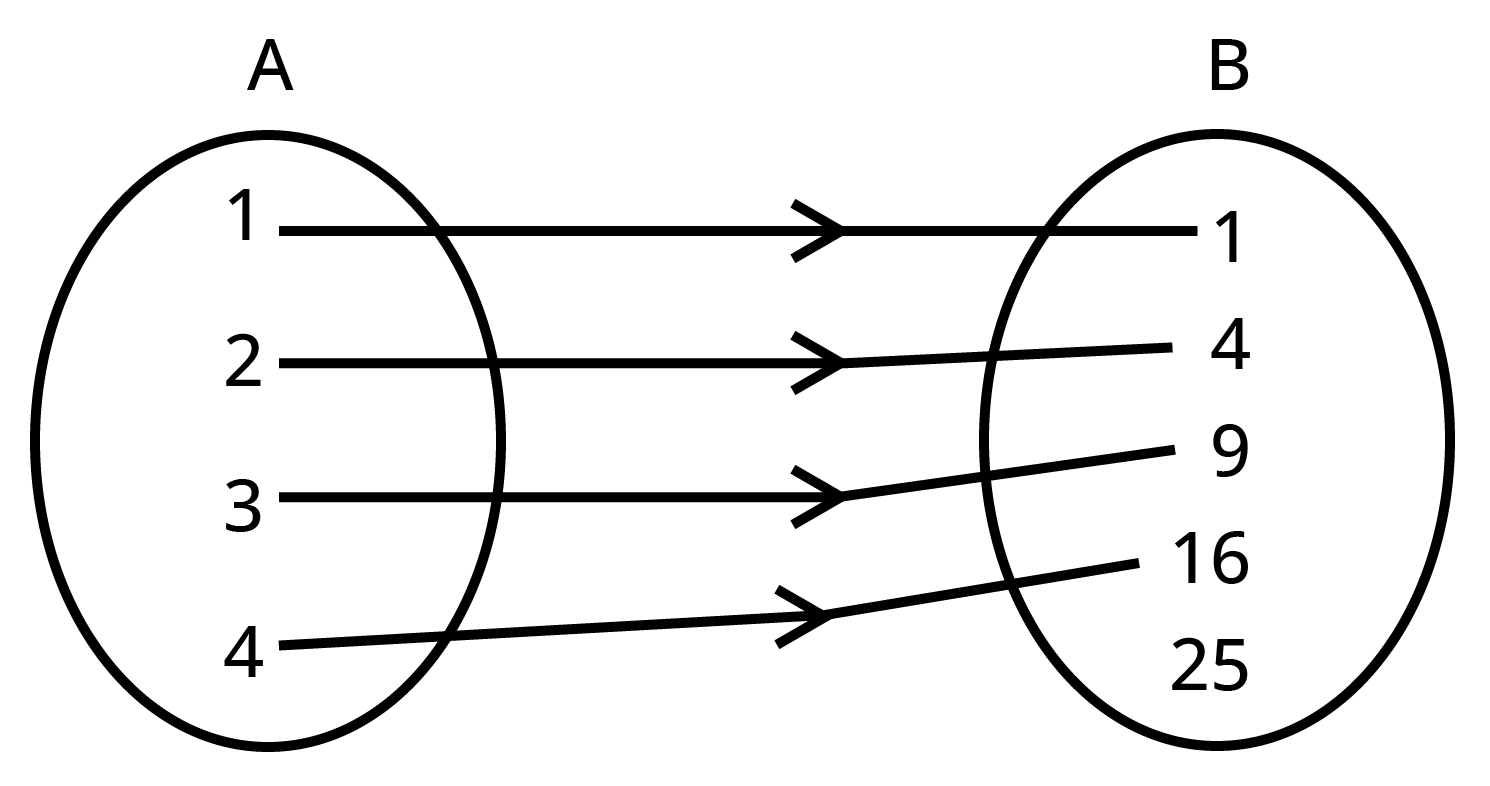
(b) Find domain of R.

Ans. The domain of the given relation $R$ is \[\left\{ \text{1,2,3,4} \right\}\].

(c) Find range of R.

Ans. The range of the given relation $R$ is \[\left\{ \text{1,4,9,16} \right\}\].

(d) Write co-domain of R.

Ans. The co-domain of the relation $R$ is \[\left\{ \text{1,4,9,16,25} \right\}\].

2. Let \[\mathbf{R}=\left\{ \left( \mathbf{x},\mathbf{y} \right)\text{ }:\mathbf{x},\mathbf{y}\in \mathbf{N}\text{ }\mathbf{and}\text{ }\mathbf{y}=\mathbf{2x} \right\}\] be a relation on $\mathbf{N}$. Find: Domain, Co-domain and Range.

Is this relation a function from $\mathbf{N}$ to $\mathbf{N}$?

Ans.  The given relation is $R=\left\{ \left( x,y \right):x,y\in \mathbb{N}\text{ and y}=\text{2x} \right\}$ on the natural number set $\mathbb{N}$.

Therefore, the domain of $R$ is the set of natural numbers $\mathbb{N}$.

The co-domain of $R$ is also the set of natural numbers $\mathbb{N}$.

And the Range of $R$ is the set of even natural numbers.

yes, the relation $R$  is a function from $N$ to $N$.

3. Find the domain and range of, \[\mathbf{f}\left( \mathbf{x} \right)=\left| \mathbf{2x}\mathbf{3} \right|\mathbf{3}\]

Ans. The given function is $f\left( x \right)=\left| 2x-3 \right|-3$.

There does not exist any value of $x$ for which $f\left( x \right)$ is unbounded. So, domain of the function $f\left( x \right)$ is the set of all real numbers $\mathbb{R}$.

Observe that, $f\left( x \right)\ge -3$, since $\left| 2x-3 \right|\ge 0$.

Therefore, the range of the function $f\left( x \right)$ is $\left[ -3,\infty  \right)$.

4. Draw the graph of the Constant function,\[\mathbf{f}:\mathbf{R}\in \mathbf{R};\text{ }\,\mathbf{f}\left( \mathbf{x} \right)=\mathbf{2x}\in \mathbf{R}\]. Also find its domain and range.

Ans. 

The domain of the function $f\left( x \right)$ is the set of all real numbers $\mathbb{R}$.

The range of the function is $\left\{ 2 \right\}$.

5.Let $\mathbf{R}=\left\{ \left( \mathbf{x,y} \right)\mathbf{:x,y}\in \mathbf{W,}\ \mathbf{2x+y}=\mathbf{8} \right\}$, then determine the following results.

(i) Find the domain and the range of R.

Ans. The provided equation is $2x+y=8$ such that $x,y\in W$.

The whole numbers for which the given equation is satisfied are as follows:

$x=0,$ $y=8$ implies $2\left( 0 \right)+8=8$,

$x=1,$ $y=6$ implies $2\left( 1 \right)+6=8$,

$x=2,\,\,y=4$ implies $2\left( 2 \right)+4=8$,

$x=3,\,\,y=2$ implies $2\left( 3 \right)+2=8$,

$x=4,\,\,y=0$ implies $2\left( 4 \right)+0=8$.

There does not have any other values of $x,y$ belong to the whole number set for which the given equation is satisfied.

Thus, the domain of the relation $R$ is $\left\{ 0,1,2,3,4 \right\}$ and the range of the relation $R$ is $\left\{ 8,6,4,2,0 \right\}$.

(ii) Write R as a set of ordered pairs.

Ans. The relation $R$ as the set of ordered pairs is given by

$R=\left\{ \left( 0,8 \right),\left( 1,6 \right),\left( 2,4 \right),\left( 3,2 \right),\left( 4,0 \right) \right\}$.

6. Let $\mathbf{R}$ be a relation from $\mathbf{Q}$ to $\mathbf{Q}$ defined by $\mathbf{R}=\left\{ \left( \mathbf{a,b} \right)\mathbf{:a,b}\in \mathbf{Q }\,\,\mathbf{and }\,\,\mathbf{a-b}\in \mathbf{Z} \right\}$. Then show the following things.

(i) $\left( \mathbf{a,a} \right)\in \mathbf{R}$ for all $\mathbf{a}\in \mathbf{Q}$.

Ans. The given relation is $R=\left\{ \left( a,b \right):a,b\in \mathbb{Q}\text{ }\,\text{and a-b}\in \mathbb{Z} \right\}$.

Let $a,a\in \mathbb{Q}$. Then $a-a=0\in \mathbb{Z}$.

Thus, $\left( a,a \right)\in R$ for all $a\in \mathbb{Q}$.

(ii) $\left( \mathbf{a,b} \right)\in \mathbf{R}$ implies that $\left( \mathbf{b,a} \right)\in \mathbf{R}$.

Ans. It is provided that $\left( a,b \right)\in \mathbb{R}$. Then $a-b\in \mathbb{Z}$, for all $a,b\in \mathbb{Q}$.

Now, $a-b\in \mathbb{Z}$  implies that $-\left( a-b \right)\in \mathbb{Z}$, that is $\left( b-a \right)\in \mathbb{Z}$.

Therefore, $\left( b,a \right)\in R$.

(iii) $\left( \mathbf{a,b} \right)\in \mathbf{R}$ and $\left( \mathbf{b},\mathbf{c} \right)\in \mathbf{R}$ implies that $\left( \mathbf{a,c} \right)\in \mathbf{R}$.

Ans. It is provided that $\left( a,b \right)\in R$ and $\left( b,c \right)\in R$.

Then, we have $a,b,c\in \mathbb{Q}$ , $a-b\in \mathbb{Z}$ and $b-c\in \mathbb{Z}$.

Therefore, $\left( a-b \right)+\left( b-c \right)\in \mathbb{Z}$

$\Rightarrow a-b+b-c\in \mathbb{Z} $

$\Rightarrow a-c\in \mathbb{Z} $

Hence, $\left( a,c \right)\in R$.

7. If $\mathbf{f}\left( \mathbf{x} \right)=\frac{{{\mathbf{x}}^{\mathbf{2}}}\mathbf{-3x+1}}{\mathbf{x-1}}$, then find $\mathbf{f}\left( -\mathbf{2} \right)+\mathbf{f}\left( \frac{\mathbf{1}}{\mathbf{3}} \right)$.

Ans. The provided function is $f\left( x \right)=\frac{{{x}^{2}}-3x+1}{x-1}$.

Substituting $x=-2$ into the function, we obtain

$f\left( -2 \right)=\frac{{{\left( -2 \right)}^{2}}-3\left( -2 \right)+1}{-2-1} $

$=\frac{4+6+1}{-3} $

$\Rightarrow f\left( -2 \right)=-\frac{11}{3}$.

Again, substituting $x=\frac{1}{3}$ into the given function, we get

$f\left( \frac{1}{3} \right)=\frac{{{\left( \frac{1}{3} \right)}^{2}}-3\times \frac{1}{3}+1}{\frac{1}{3}-1}$

 $=\frac{\frac{1}{9}-1+1}{-\frac{2}{3}} $

 $=-\frac{1}{9}\times \frac{3}{2} $

$\Rightarrow f\left( \frac{1}{3} \right)=-\frac{1}{6}$.

Hence, $f\left( -2 \right)+f\left( \frac{1}{3} \right)=-\frac{11}{3}-\frac{1}{6}=\frac{-22-1}{6}=\frac{-23}{6}=-3\frac{5}{6}$.

8. Find the domain and the range of the function $\mathbf{f}\left( \mathbf{x} \right)=\mathbf{3}{{\mathbf{x}}^{\mathbf{2}}}-\mathbf{5}$. Also find $\mathbf{f}\left( -\mathbf{3} \right)$ and the numbers which are associated with the number $\mathbf{43}$ in its range.

Ans. The provided function is $f\left( x \right)=3{{x}^{2}}-5$.

Since, for all the real value of $x$, the function is valid, so the domain of the function $f\left( x \right)$ is the set of all real numbers $\mathbb{R}$.

Again, since the term $3{{x}^{2}}\ge 0$, so $3{{x}^{2}}-5\ge -5$, that is $f\left( x \right)\ge -5$.

Therefore, the range of the function $f\left( x \right)$ is $\left[ -5,\infty  \right)$.

Now, substituting $x=-3$ into the given function we get,

$f\left( -3 \right)=3{{\left( -3 \right)}^{2}}-5 $

$=3\times 9-5 $

$\Rightarrow f\left( -3 \right)=22$.

Again, substituting $f\left( x \right)=43$,we get

$43=3{{x}^{2}}-5$

  $\Rightarrow 3{{x}^{2}}=48 $

 $\Rightarrow {{x}^{2}}=16 $

 $\Rightarrow x=\pm 4 $

Hence, the numbers that are associated with the number $43$ in the range of the given function $f\left( x \right)$ are $-4,\,4$.

9. If \[\mathbf{f}\left( \mathbf{x} \right)={{\mathbf{x}}^{\mathbf{2}}}\mathbf{-3x+1}\], find $\mathbf{x}$ such that $\mathbf{f}\left( \mathbf{2x} \right)=\mathbf{f}\left( \mathbf{x} \right)$.

Ans. The provided function is $f\left( x \right)={{x}^{2}}-3x+1$.

Now, replacing $x$ by $2x$ into the given function, we obtain

$f\left( 2x \right)={{\left( 2x \right)}^{2}}-3\left( 2x \right)+1$

$\Rightarrow f\left( 2x \right)=4{{x}^{2}}-6x+1$.

Now, it is provided that, $f\left( 2x \right)=f\left( x \right)$

$\Rightarrow 4{{x}^{2}}-6x+1={{x}^{2}}-3x+1 $

 $\Rightarrow 3{{x}^{2}}-3x=0 $

 $\Rightarrow 3x\left( x-1 \right)=0 $

 $\Rightarrow x=0,\,1 $

Hence, the values of $x$ are $0,\,\,1$.

10. Find the domain and the range of the function $\mathbf{f}\left( \mathbf{x} \right)=\sqrt{\mathbf{x}-\mathbf{1}}$.

Ans. The provided function is $f\left( x \right)=\sqrt{x-1}$.

Observe that, the function is valid when $x-1\ge 0$.

That is, when $x\ge 1$.

Therefore, the domain of the function $f\left( x \right)$ is $\left[ 1,\infty  \right)$.

Now, observe that, the function $f\left( x \right)$ can have all the positive real numbers including zero.

Thus, the domain of the function $f\left( x \right)$ is $\left[ 0,\infty  \right)$.

11. Let $\mathbf{R}=\left\{ \left( \mathbf{0,0} \right)\mathbf{,}\left( \mathbf{2,4} \right)\mathbf{,}\left( \mathbf{-1,}-\mathbf{2} \right)\mathbf{,}\left( \mathbf{3,6} \right)\mathbf{,}\left( \mathbf{1,2} \right) \right\}$ be a relation, then answer the following questions.

(i) write domain of $\mathbf{R}$.

Ans. The provided relation is $R=\left\{ \left( 0,0 \right),\left( 2,4 \right),\left( -1,-2 \right),\left( 3,6 \right),\left( 1,2 \right) \right\}$.

So, the domain of the relation $R$ is $\left\{ 0,2,-1,3,1 \right\}$.

(ii) write range of $\mathbf{R}$.

Ans. The range of the relation $R$ is $\left\{ 0,4,-2,6,2 \right\}$.

(iii) write $\mathbf{R}$ the set builder form.

Ans. The set builder form of the provided relation is given by

$R=\left\{ \left( x,y \right):x\in \mathbb{Z},\,\,-1\le x\le 3,\,\,y=2x \right\}$.

(iv) represent $\mathbf{R}$ by an arrow diagram.

Ans.  The following arrow diagram represents the given relation $R$.

12. Let $\mathbf{A}=\left\{ \mathbf{1},\mathbf{2},\mathbf{3} \right\}$, $\mathbf{B}=\left\{ \mathbf{1},\mathbf{2},\mathbf{3},\mathbf{4} \right\}$ and $\mathbf{R}=\left\{ \left( \mathbf{x},\mathbf{y} \right):\left( \mathbf{x},\mathbf{y} \right)\in \mathbf{A}\times \mathbf{B},\mathbf{y}=\mathbf{x}+\mathbf{1} \right\}$. Determine the following results.

(i) find $\mathbf{A}\times \mathbf{B}$.

Ans. The provided relation is $R=\left\{ \left( x,y \right):\left( x,y \right)\in A\times B,\ \ y=x+1 \right\}$.

Also, the given sets are $A=\left\{ 1,2,3 \right\}$ and $B=\left\{ 1,2,3,4 \right\}$.

Therefore, the cartesian product of the sets,

$A\times B=\left\{ \left( 1,1 \right),\left( 1,2 \right),\left( 1,3 \right),\left( 1,4 \right),\left( 2,1 \right),\left( 2,2 \right),\left( 2,3 \right),\left( 2,4 \right),\left( 3,1 \right), \right. $

 $\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left. \left( 3,2 \right),\left( 3,3 \right),\left( 3,4 \right) \right\} $

(ii) write $\mathbf{R}$ in roster form.

Ans. The provided relation $R$ in roster form is given by

$R=\left\{ \left( 1,2 \right),\left( 2,3 \right),\left( 3,4 \right) \right\}$.

(iii) write domain $range of $\mathbf{R}$.

Ans. The domain of the relation $R$ is $\left\{ 1,2,3 \right\}$ and range of the relation $R$ is $\left\{ 2,3,4 \right\}$.

(iv) represent $\mathbf{R}$ by an arrow diagram.

Ans. The following arrow diagram represents the relation $R=\left\{ \left( x,y \right):\left( x,y \right)\in A\times B,\ \ y=x+1 \right\}$.

13. The cartesian product $\mathbf{A}\times \mathbf{A}$ has $\mathbf{9}$ elements among which are found $\left( \mathbf{-1,0} \right)$ and $\left( \mathbf{0},\mathbf{1} \right)$. Find the set and the remaining \[\]

find the set and the remaining elements of $\mathbf{A}\times \mathbf{A}$.

Ans.  Suppose that $n\left( A \right)=m$.

It is provided that, $n\left( A\times A \right)=9$

$\Rightarrow n\left( A \right)\cdot n\left( A \right)=9$

$\Rightarrow {{\left[ n\left( A \right) \right]}^{2}}=9 $

 $\Rightarrow n\left( A \right)=3,\ \ \,\,\left[ \because n\left( A \right)>0 \right] $

Again, the ordered pairs $\left( -1,0 \right),\left( 0,1 \right)\in A\times A$ implies that \[-1,0,1\in A\].

Also, the number elements in $A$ is $n\left( A \right)=3$.

Thus, $A=\left\{ -1,0,1 \right\}$.

Hence, the remaining elements of the cartesian product $A\times A$ is given by

$\left( -1,-1 \right),\left( -1,1 \right),\left( 0,-1 \right),\left( 0,0 \right),\left( 1,-1 \right),\left( 1,0 \right),$ and $\left( 1,1 \right)$.

14. Find the domain and the range of the function $\mathbf{f}\left( \mathbf{x} \right)=\frac{\mathbf{1}}{\sqrt{\mathbf{5}-\mathbf{x}}}$.

Ans. The provided function is $f\left( x \right)=\frac{1}{\sqrt{5-x}}$.

$f\left( x \right)$ is valid when $5-x>0$. That is, when $x<5$.

Therefore, the domain of the function $f\left( x \right)$ is $\left( -\infty ,5 \right)$.

Again, the function $f\left( x \right)$ can have all the positive real numbers.

Thus, the range of the function $f\left( x \right)$ is $\left( 0,\infty  \right)$.

15. Let $\mathbf{f}\left( \mathbf{x} \right)=\mathbf{x}+\mathbf{1}$ and $\mathbf{g}\left( \mathbf{x} \right)=\mathbf{2x}-\mathbf{3}$ be two real functions. Find the following functions.

(i) $\mathbf{f}+\mathbf{g}$

Ans. The provided functions are $f\left( x \right)=x+1$ and $g\left( x \right)=2x-3$.

Then the function $\left( f+g \right)\left( x \right)=f\left( x \right)+g\left( x \right)$

 $=\left( x+1 \right)+\left( 2x-3 \right) $

 $=3x-2 $

That is, $\left( f+g \right)\left( x \right)=3x-2$, for all $x\in \mathbb{R}$.

(ii) $\mathbf{f}-\mathbf{g}$

Ans. The function $\left( f-g \right)\left( x \right)=f\left( x \right)-g\left( x \right)$

 $=\left( x+1 \right)-\left( 2x-3 \right) $

 $=x+1-2x+3 $

 $=-x+4 $

Thus, $\left( f-g \right)\left( x \right)=-x+4$, for all $x\in \mathbb{R}$.

(iii) $\mathbf{fg}$

Ans. The function $\left( fg \right)\left( x \right)=f\left( x \right)g\left( x \right)$

$=\left( x+1 \right)\left( 2x-3 \right)$

$=2{{x}^{2}}-x-3$, for all $x\in \mathbb{R}$.

Thus, $\left( fg \right)\left( x \right)=2{{x}^{2}}-x-3$  for all $x\in \mathbb{R}$.

(iv) $\frac{\mathbf{f}}{\mathbf{g}}$

Ans. The function $\left( \frac{f}{g} \right)\left( x \right)=\frac{f\left( x \right)}{g\left( x \right)}$, $g\left( x \right)\ne 0$.

Then, $\left( \frac{f}{g} \right)\left( x \right)=\frac{x+1}{2x-3},\ \ x\ne \frac{3}{2},\ \ x\in \mathbb{R}$.

(v) ${{\mathbf{f}}^{\mathbf{2}}}-\mathbf{3g}$

Ans. The function $\left( {{f}^{2}}-3g \right)\left( x \right)={{f}^{2}}\left( x \right)-3g\left( x \right)$

$=f\left( x \right)\cdot f\left( x \right)-3g\left( x \right)$

$=\left( x+1 \right)\left( x+1 \right)-3\left( 2x-3 \right) $

$={{x}^{2}}+2x+1-6x+9 $

$\Rightarrow \left( {{f}^{2}}-3g \right)\left( x \right)={{x}^{2}}-4x+10$ for all $x\in \mathbb{R}$.

16. Find the domain and the range of the following functions

(i) $\mathbf{f}\left( \mathbf{x} \right)=\frac{\mathbf{x}-\mathbf{3}}{\mathbf{2x}+\mathbf{1}}$

Ans.  The provided function is $f\left( x \right)=\frac{x-3}{2x+1}$.

Observe that, the function $f\left( x \right)$ becomes unbounded when $2x+1\ne 0$, that is, when $x\ne -\frac{1}{2}$.

Therefore, the domain of the function $f\left( x \right)$ is $\mathbb{R}-\left\{ -\frac{1}{2} \right\}$.

Now, let $f\left( x \right)=y$. Then, rewriting the given function, we get

$y=\frac{x-3}{2x+1} $

$\Rightarrow 2xy+y=x-3 $

$\Rightarrow 2xy-x=-3-y $

$\Rightarrow x\left( 2y-1 \right)=-3-y $

$\Rightarrow x=\frac{3+y}{1-2y}$, which is valid only if $1-2y\ne 0$, that is, if $y\ne \frac{1}{2}$.

Hence, the range of the function $f\left( x \right)$ is $\mathbb{R}-\left\{ \frac{1}{2} \right\}$.

(ii) $\mathbf{f}\left( \mathbf{x} \right)=\frac{{{\mathbf{x}}^{\mathbf{2}}}}{\mathbf{1}+{{\mathbf{x}}^{\mathbf{2}}}}$
Ans. The provided function is $f\left( x \right)=\frac{{{x}^{2}}}{1+{{x}^{2}}}$.

Observe that, $1+{{x}^{2}}\ne 0$. Therefore, the function is defined for all real numbers.

Thus, the domain of the function $f\left( x \right)$ is the set of all real numbers $\mathbb{R}$.

Now, rewrite the given function in terms of $x$, taking $f\left( x \right)=y$.

$y=\frac{{{x}^{2}}}{1+{{x}^{2}}}$

  $\Rightarrow y+{{x}^{2}}y={{x}^{2}} $

 $\Rightarrow {{x}^{2}}\left( 1-y \right)=y $

 $\Rightarrow {{x}^{2}}=\frac{y}{1-y} $

$\Rightarrow x=\sqrt{\frac{y}{1-y}}$, which is valid if $\frac{y}{1-y}\ge 0$, 

i.e., if $y\left( 1-y \right)\ge 0$,

i.e., if $-y\left( y-1 \right)\ge 0$,

i.e., if $y\ge 0$ and $y-1<0$, since $y$ should not be $1$.

i.e., if $0\le y<1$.

Hence, the range of the function $f\left( x \right)$ is $\left[ 0,1 \right)$.

(iii) $\mathbf{f}\left( \mathbf{x} \right)=\frac{\mathbf{1}}{\mathbf{1}-{{\mathbf{x}}^{\mathbf{2}}}}$

Ans. The provided function is $f\left( x \right)=\frac{1}{1-{{x}^{2}}}$.

Observe that, the function $f\left( x \right)$ is valid only when $1-{{x}^{2}}\ne 0$.

i.e., when ${{x}^{2}}\ne 1$

i.e., when $x\ne -1,1$.

Thus, the domain of the function $f\left( x \right)$ is $\mathbb{R}-\left\{ -1,1 \right\}$.

Now, let $f\left( x \right)=y$ and rewrite the function in terms of $x$.

 $y=\frac{1}{1-{{x}^{2}}} $

 $\Rightarrow y-y{{x}^{2}}=1 $

 $\Rightarrow {{x}^{2}}=1-\frac{1}{y} $

$\Rightarrow x=\sqrt{1-\frac{1}{y}}$, which is valid if $1-\frac{1}{y}\ge 0$, 

i.e., if $y\left( y-1 \right)\ge 0$, multiplying by a positive real number ${{y}^{2}}$.

i.e., if $y<0$ or $y\ge 1$, since $y$ should not be $0$.

Thus, the range of the function $f\left( x \right)$ is $\left( -\infty ,0 \right)\cup \left( 1,\infty  \right)$.

17. If $\mathbf{A}=\left\{ \mathbf{1,2,3} \right\}$, $\mathbf{B}=\left\{ \mathbf{3,4} \right\}$, and $C=\left\{ \mathbf{4},\mathbf{5},\mathbf{6} \right\}$. Then find the following sets.

(i) $\mathbf{A}\times \left( \mathbf{B}\cup \mathbf{C} \right)$

Ans. The given sets are $A=\left\{ 1,2,3 \right\}$, $B=\left\{ 3,4 \right\}$ and $C=\left\{ 4,5,6 \right\}$.

Then, $B\cup C=\left\{ 3,4,5,6 \right\}$.

Therefore, $A\times \left( B\cup C \right)=\left\{ 1,2,3 \right\}\times \left\{ 3,4,5,6 \right\}$

$=\left\{ \left( 1,3 \right),\left( 1,4 \right),\left( 1,5 \right),\left( 1,6 \right),\left( 2,3 \right),\left( 2,4 \right),\left( 2,5 \right),\left( 2,6 \right),\left( 3,3 \right),\left( 3,4 \right),\left( 3,5 \right),\left. \left( 3,6 \right) \right\} \right.$

(ii) $\mathbf{A}\times \left( \mathbf{B}\cap \mathbf{C} \right)$

Ans. The set $B\cap C=\left\{ 3,4 \right\}\cap \left\{ 4,5,6 \right\}=\left\{ 4 \right\}$.

Therefore, the cartesian product set,

$A\times \left( B\cap C \right)=\left\{ 1,2,3 \right\}\times \left\{ 4 \right\}=\left\{ \left( 1,4 \right),\left( 2,4 \right),\left( 3,4 \right) \right\}$.

(iii) $\left( \mathbf{A}\times \mathbf{B} \right)\cap \left( \mathbf{B}\times \mathbf{C} \right)$

Ans. The cartesian product set,

$A\times B=\left\{ 1,2,3 \right\}\times \left\{ 3,4 \right\}$

$=\left\{ \left( 1,3 \right),\left( 1,4 \right),\left( 2,3 \right),\left( 2,4 \right),\left( 3,3 \right),\left( 3,4 \right) \right\}$.

Also, the cartesian product set,

$B\times C=\left\{ 3,4 \right\}\times \left\{ 4,5,6 \right\}$

$\Rightarrow B\times C=\left\{ \left( 3,4 \right),\left( 3,5 \right),\left( 3,6 \right),\left( 4,4 \right),\left( 4,5 \right),\left( 4,6 \right) \right\}$.

Thus, $\left( A\times B \right)\cap \left( B\times C \right)=\left\{ \left( 3,4 \right) \right\}$.

18. For non-empty sets $\mathbf{A}$ and $\mathbf{B}$ prove that $\left( \mathbf{A}\times \mathbf{B} \right)=\left( \mathbf{B}\times \mathbf{A} \right)\Leftrightarrow \mathbf{A}=\mathbf{B}$.

Ans. First suppose that, the sets are equal, that is, $A=B$.

Then, $\left( A\times B \right)=\left( A\times A \right)$.

Also, $\left( B\times A \right)=\left( A\times A \right)$.

Therefore, $\left( A\times B \right)=\left( B\times A \right)$.

Again, conversely suppose that, $\left( A\times B \right)=\left( B\times A \right)$.

So, let $x\in A$. Then there exists $b\in B$ such that $\left( x,b \right)\in A\times B$.

This implies, $\left( x,b \right)\in B\times A$.

Therefore, $x\in B$.

Thus, $A\subseteq B$.

In a similar manner, also it can be shown that $B\subseteq A$.

Thus, $A=B$.

Hence, the required result is proved.

19. Let $\mathbf{m}$ be a given fixed positive integer. Let $\mathbf{R}=\left\{ \left( \mathbf{a},\mathbf{b} \right):\mathbf{a,b}\in \mathbf{Z}\text{ }\mathbf{and}\,\,\left( \mathbf{a}-\mathbf{b} \right)\text{ }\mathbf{is}\,\ \mathbf{divisible}\,\,\mathbf{by}\,\,\mathbf{m} \right\}$. Then show that $\mathbf{R}$ is an equivalence relation on $\mathbf{Z}$.

Ans. The given relation is $R=\left\{ \left( a,b \right):a,b\in \mathbb{Z}\text{ and }\left( a-b \right)\text{ is divisible by m} \right\}$.

First, suppose that, $a,a\in \mathbb{Z}$.

Then, $a-a=0$, which is divisible by $m$.

Thus, $\left( a,a \right)\in R$, that is, $R$ is reflexive.

Again, let $\left( a,b \right)\in R$. Then, $\left( a-b \right)$ is divisible by $m$.

Therefore, $-\left( a-b \right)$ is divisible by $m$.

That is, $\left( b-a \right)$ is divisible by $m$.

Thus, $\left( b,a \right)\in R$.

So, $R$ is symmetric.

Now, let $\left( a,b \right),\left( b,c \right)\in R$. Then, $\left( a-b \right)$ is divisible by $m$ and $\left( b-c \right)$ is divisible by $m$.

Therefore, by the law of divisibility, 

$\left( a-b \right)+\left( b-c \right)$ is divisible by $m$.

i.e., $a-b+b-c$ is divisible by $m$.

i.e., $a-c$ is divisible by $m$.

Thus, $R$ is transitive.

Hence, $R$ is reflexive, symmetric and transitive, and so, $R$ becomes an equivalence relation.

20. Let $\mathbf{A}=\left\{ \mathbf{1,2,3,4,5} \right\}$ and $\mathbf{B}=\left\{ \mathbf{1},\mathbf{3},\mathbf{4} \right\}$. Let $\mathbf{R}$ be the relation, is greater than from $\mathbf{A}$ to $\mathbf{B}$. Write $\mathbf{R}$ as a set of ordered pairs. find domain$\left( \mathbf{R} \right)$ and range$\left( \mathbf{R} \right)$.

Ans. The given sets are $A=\left\{ 1,2,3,4,5 \right\}$ and

$B=\left\{ 1,3,4 \right\}$.

Since, the relation $R$ is such that $A$ is greater than from $B$, so it will be

$R=\left\{ \left( 2,1 \right),\left( 3,1 \right),\left( 3,2 \right),\left( 4,1 \right),\left( 4,2 \right),\left( 4,3 \right),\left( 5,1 \right),\left( 5,3 \right),\left( 5,4 \right) \right\}$.

Therefore, the domain of the relation is $\left\{ 2,3,4,5 \right\}$ and range of the relation $R$ is $\left\{ 1,3,4 \right\}$.

21. Define modulus function Draw graph.

Ans. Suppose that, $f:\mathbb{R}\to \mathbb{R}$ be the modulus function such that

$f\left( x \right)=\left| x \right|$, for all $x\in \mathbb{R}$. 

Therefore, $f\left( x \right)=\left| x \right|=\left\{ \begin{align}x,\,\,\,\,\,if\ \ x\ge 0 \\-x,\,\,\,if\,\,x<0 \end{align} \right.$

Since, $\left| x \right|\ge 0$,  $\forall ,\,\,x\in \mathbb{R}$, so the domain of the modulus function is the set of all real numbers $\mathbb{R}$ and the range of $f\left( x \right)$ is the set ${{\mathbb{R}}^{+}}\cup \left\{ 0 \right\}$.

Now, to draw the graph of the modulus function, consider the following table of values.

Plot the above points on a graph paper such that $A\left( -3,3 \right),B\left( -2,2 \right),C\left( -1,1 \right),D\left( 0,0 \right),E\left( 1,1 \right),F\left( 2,2 \right),$ and $G\left( 4,4 \right)$.

Then, join the plotted points by straight lines.

Then, the graph of the modulus function obtained is given by

22. Let $\mathbf{A}=\left\{ \mathbf{1},\mathbf{2} \right\}$ and $\mathbf{B}=\left\{ \mathbf{3},\mathbf{4} \right\}$. Write $\mathbf{A}\times \mathbf{B}$. How many subsets will $\mathbf{A}\times \mathbf{B}$ have? List them.

Ans. The given sets are $A=\left\{ 1,2 \right\}$ and $B=\left\{ 3,4 \right\}$.

Then, $A\times B=\left\{ \left( 1,3 \right),\left( 1,4 \right),\left( 2,3 \right),\left( 2,4 \right) \right\}$.

There is total ${{2}^{4}}=16$ subsets of the set $A\times B$.

The list of subsets is given by

$\phi ,\left\{ \left( 1,3 \right) \right\},\left\{ \left( 1,4 \right) \right\},\left\{ \left( 2,3 \right) \right\},\left\{ \left( 2,4 \right) \right\},\left\{ \left( 1,4 \right) \right\},\left\{ \left( 1,3 \right) \right\},\left\{ \left( 2,3 \right) \right\},\left\{ \left( 1,3 \right) \right\},\left\{ \left( 2,4 \right) \right\},$$\left\{ \left( 1,4 \right),\left( 2,3 \right) \right\}$, $\left\{ \left( 1,4 \right),\left( 2,4 \right) \right\},\left\{ \left( 2,3 \right),\left( 2,4 \right) \right\},\left\{ \left( 1,3 \right),\left( 1,4 \right),\left( 2,3 \right) \right\},$$\left\{ \left( 1,3 \right),\left( 1,4 \right),\left( 2,4 \right) \right\}$, $\left\{ \left( 1,3 \right),\left( 2,3 \right),\left( 2,4 \right) \right\},\left\{ \left( 1,4 \right),\left( 2,3 \right),\left( 2,4 \right) \right\}$.

23. Let $\mathbf{A}=\left\{ \mathbf{1},\mathbf{2} \right\}$, $\mathbf{B}=\left\{ \mathbf{1},\mathbf{2},\mathbf{3},\mathbf{4} \right\},\,\,\mathbf{C}=\left\{ \mathbf{5},\mathbf{6} \right\}$ and $\mathbf{D}=\left\{ \mathbf{5},\mathbf{6},\mathbf{7},\mathbf{8} \right\}$. Then verify the following statements.

(i) $\mathbf{A}\times \left( \mathbf{B}\cap \mathbf{C} \right)=\left( \mathbf{A}\times \mathbf{B} \right)\cap \left( \mathbf{A}\times \mathbf{C} \right)$

Ans. The given sets are $A=\left\{ 1,2 \right\}$, $B=\left\{ 1,2,3,4 \right\}$, $C=\left\{ 5,6 \right\}$ and $D=\left\{ 5,6,7,8 \right\}$.

Then, $B\cap C=\left\{ 1,2,3,4 \right\}\cap \left\{ 5,6 \right\}=\phi $.

Therefore, $A\times \left( B\cap C \right)=A\times \phi =\phi $.                                    …… (i)

Now, $A\times B=\left\{ 1,2 \right\}\times \left\{ 1,2,3,4 \right\}$

$=\left\{ \left( 1,1 \right),\left( 1,2 \right),\left( 1,3 \right),\left( 1,4 \right),\left( 2,1 \right),\left( 2,2 \right),\left( 2,3 \right),\left( 2,4 \right) \right\}$.

Also, $A\times C=\left\{ 1,2 \right\}\times \left\{ 5,6 \right\}$

$=\left\{ \left( 1,5 \right),\left( 1,6 \right),\left( 2,5 \right),\left( 2,6 \right) \right\}$.

So, $\left( A\times B \right)\cap \left( A\times C \right)=\phi $                                              …… (ii)

Equation (i) and (ii) together implies that,

$A\times \left( B\cap C \right)=\left( A\times B \right)\cap \left( A\times C \right)$.

(ii) $\mathbf{A}\times \mathbf{C}$ is a subset of $\mathbf{B}\times \mathbf{D}$.

Ans. The cartesian product,

$A\times C=\left\{ \left( 1,5 \right),\left( 1,6 \right),\left( 2,5 \right),\left( 2,6 \right) \right\}$.

Also, $B\times D=\left\{ 1,2,3,4 \right\}\times \left\{ 5,6,7,8 \right\}$

$=\left\{ \left( 1,5 \right),\left( 1,6 \right),\left( 1,7 \right),\left( 1,8 \right),\left( 2,5 \right),\left( 2,6 \right),\left( 2,7 \right),\left( 2,8 \right) \right\}$.

Therefore, it is found that, $\left( A\times C \right)\subset \left( B\times D \right)$.

24. Find the domain and the range of the relation $\mathbf{R}$ defined by

$\mathbf{R}=\left\{ \left( \mathbf{x}+\mathbf{1},\mathbf{x}+\mathbf{3} \right):\mathbf{x}\in \left( \mathbf{0},\mathbf{1},\mathbf{2},\mathbf{3},\mathbf{4},\mathbf{5} \right) \right\}$.

Ans. For $x\in \left\{ 0,1,2,3,4,5 \right\}$, the values of the ordered pairs $\left( x+1,x+3 \right)$ for the relation $\text{R}=\left\{ \left( \text{x+1,x+3} \right)\text{:x}\in \left( \text{0,1,2,3,4,5} \right) \right\}$ can be obtained as,

$x=0\,\,\,\Rightarrow \left( 0+1,0+3 \right)=\left( 1,3 \right)\in R$,

$x=1\ \ \Rightarrow \left( 1+1,1+3 \right)=\left( 2,4 \right)\in R$,

$x=2\,\,\,\Rightarrow \left( 2+1,2+3 \right)=\left( 3,5 \right)\in R$,

$x=3\,\,\,\Rightarrow \left( 3+1,3+3 \right)=\left( 4,6 \right)\in R$,

$x=4\,\,\,\Rightarrow \left( 4+1,4+3 \right)=\left( 5,7 \right)\in R$,

$x=5\,\,\,\Rightarrow \left( 5+1,5+3 \right)=\left( 6,8 \right)\in R$.

Hence, the domain of the relation $R$ is $\left\{ 1,2,3,4,5,6 \right\}$ and range of relation $R$ is $\left\{ 3,4,5,6,7,8 \right\}$.

25. Find the linear relation between the components of the ordered pairs of the relation $\mathbf{R}$, where $\mathbf{R}=\left\{ \left( \mathbf{2},\mathbf{1} \right),\left( \mathbf{4},\mathbf{7} \right),\left( \mathbf{1},-\mathbf{2} \right),... \right\}$.

Ans. The provided relation is $R=\left\{ \left( 2,1 \right),\left( 4,7 \right),\left( 1,-2 \right),... \right\}$.

Suppose that, $y=ax+b$ is the linear relation between the components of $R$. As $\left( 2,1 \right)\in R$, so $y=ax+b$$\Rightarrow 1=2a+b$    …… (i)

Again, $\left( 4,7 \right)\in R$. So, $7=4a+b$                      …… (ii)

Subtract the equation (i) from the equation (ii). Then it yields

$2a=6$

$\Rightarrow a=3$.

So, substituting $a=3$ into the equation (i), yields

$1=6+b$

$\Rightarrow b=-5$.

Substituting the obtained values of $a,b$ into the assumed linear function, gives $y=3x-5$.

Hence, the required linear relation between the components of the ordered pairs of the relation $R$ is $y=3x-5$.

26. Let $\mathbf{A}=\left\{ \mathbf{1},\mathbf{2},\mathbf{3},\mathbf{4},\mathbf{5},\mathbf{6} \right\}$. Define a relation $\mathbf{R}$ from $\mathbf{A}$ to $\mathbf{A}$ by

$\mathbf{R}=\left\{ \left( \mathbf{x},\mathbf{y} \right):\mathbf{y}=\mathbf{x}+\mathbf{1},\mathbf{x},\mathbf{y}\in \mathbf{A} \right\}$. Then answer the questions.

(i) write $\mathbf{R}$ in the roaster form.

Ans. The given set is $A=\left\{ 1,2,3,4,5,6 \right\}$ and the given relation $R:A\to A$ is $R=\left\{ \left( x,y \right):y=x+1,\ \ x,y\in A \right\}$.

The linear equation $y=x+1$ for $x,y\in A$ gives the following ordered pairs.

$x=1\,\,\Rightarrow \,\,y=1+1=2$

$x=2\ \ \Rightarrow y=2+1=3$

$x=3\,\,\Rightarrow y=3+1=4$

$x=4\,\,\Rightarrow y=4+1=5$

$x=5\,\,\Rightarrow y=5+1=6$.

Thus, the roaster form of the relation $R$ is given by

$R=\left\{ \left( 1,2 \right),\left( 2,3 \right),\left( 3,4 \right),\left( 4,5 \right),\left( 5,6 \right) \right\}$.

(ii) write down the domain, co-domain and range of $\mathbf{R}$.

Ans. The domain of the relation $R$ is $\left\{ 1,2,3,4,5 \right\}$, co-domain of the relation $R$ is $A$, and the range of the relation $R$ is $\left\{ 2,3,4,5,6 \right\}$.

(iii) Represent $\mathbf{R}$ by an arrow diagram.

Ans. The following arrow diagram represent the given relation $R=\left\{ \left( x,y \right):y=x+1,\ \ x,y\in A \right\}$.

27. A relation $'\,\mathbf{f}'$ is defined by $\mathbf{f}:\mathbf{x}\to {{\mathbf{x}}^{\mathbf{2}}}-\mathbf{2}$ where $\mathbf{x}\in \left\{ -\mathbf{1},-\mathbf{2},\mathbf{0},\mathbf{2} \right\}$. Then answer the following questions.

(i) list the elements of $\mathbf{f}$.

Ans. The given relation $f$ is defined as $f:x\to {{x}^{2}}-2$ such that $x\in \left\{ -1,-2,0,2 \right\}$, that is $f\left( x \right)={{x}^{2}}-2$.

So, substituting $x=-1,-2,0,2$ successively into the relation $f\left( x \right)$, we get

$f\left( -1 \right)={{\left( -1 \right)}^{2}}-2=1-2=-1$

$f\left( -2 \right)={{\left( -2 \right)}^{2}}-2=4-2=2$

$f\left( 0 \right)={{0}^{2}}-2=-2$

$f\left( 2 \right)={{2}^{2}}-2=4-2=2$.

Thus, the list of the elements of $f$ is given by

$f=\left\{ \left( -1,-1 \right),\left( -2,2 \right),\left( 0,-2 \right),\left( 2,2 \right) \right\}$.

(ii) is $\mathbf{f}$ a function?

Ans. Observe that, all the elements of the domain of the relation $f$ correspond to distinct images. 

Hence, the relation $f$ is a function.

28. If $\mathbf{y}=\frac{\mathbf{6x}-\mathbf{5}}{\mathbf{5x}-\mathbf{6}}$. Prove that $\mathbf{f}\left( \mathbf{y} \right)=\mathbf{x},\,\,\mathbf{x}\ne \frac{\mathbf{6}}{\mathbf{5}}$. 

Ans. The given equation is $y=\frac{6x-5}{5x-6}$.

Now, let $f\left( x \right)=\frac{6x-5}{5x-6}$.

Therefore, $f\left( y \right)=\frac{6y-5}{5y-6}$

$=\frac{6\times \left( \frac{6x-5}{5x-6} \right)-5}{5\times \left( \frac{6x-5}{5x-6} \right)-6}$  [substituting the value of $y$]

That is,

$f\left( y \right)=\frac{36x-30-25x+30}{5x-6}\times \frac{5x-6}{30x-25-30x+36}$

$\Rightarrow f\left( y \right)=\frac{11x}{11}$

Hence, $f\left( y \right)=x$, $x\ne \frac{6}{5}$.

29. Let $\mathbf{f}:\mathbf{X}\to \mathbf{Y}$ be defined by $\mathbf{f}\left( \mathbf{x} \right)={{\mathbf{x}}^{\mathbf{2}}}$ for all $\mathbf{x}\in \mathbf{X}$ where $\mathbf{X}=\left\{ -\mathbf{2},-\mathbf{1},\mathbf{0},\mathbf{1},\mathbf{2},\mathbf{3} \right\}$ and write the relation $\mathbf{f}$ in the roaster form. Is $\mathbf{f}$ a function?

Ans. The given function is $f:X\to Y$ defined as

$f\left( x \right)={{x}^{2}}$, for all $x\in X=\left\{ -2,-1,0,1,2,3 \right\}$ and

$y=\left\{ 0,1,4,7,9,10 \right\}$.

Then, $f\left( -2 \right)={{\left( -2 \right)}^{2}}=4$

$f\left( -1 \right)={{\left( -1 \right)}^{2}}=1$

$f\left( 0 \right)={{0}^{2}}=0$

$f\left( 1 \right)={{1}^{2}}=1$

$f\left( 2 \right)={{2}^{2}}=4$

$f\left( 3 \right)={{3}^{2}}=9$

Therefore, $f=\left\{ \left( -2,4 \right),\left( -1,1 \right),\left( 0,0 \right),\left( 1,1 \right),\left( 2,4 \right),\left( 3,9 \right) \right\}$.

Since, each of the element in $X$ has distinct image in $Y$, so, $f$ is a function.

30. Determine a quadratic function $'\,\mathbf{f}\,'$ defined by

$\mathbf{f}\left( \mathbf{x} \right)=\mathbf{a}{{\mathbf{x}}^{\mathbf{2}}}\mathbf{+bx+c}$ if $\mathbf{f}\left( \mathbf{0} \right)=\mathbf{6}$, $\mathbf{f}\left( \mathbf{2} \right)=\mathbf{11}$, and $\mathbf{f}\left( -\mathbf{3} \right)=\mathbf{6}$.

Ans. The given quadratic function is $f\left( x \right)=a{{x}^{2}}+bx+c$.

Since, $f\left( 0 \right)=6$, so

  $a{{\left( 0 \right)}^{2}}+b\left( 0 \right)+c=6 $

 $\Rightarrow c=6 $

Again, $f\left( 2 \right)=11$

  $\Rightarrow a{{\left( 2 \right)}^{2}}+b\left( 2 \right)+6=11 $

 $\Rightarrow 4a+2b+6=11 $

$\Rightarrow 4a+2b=5$                                             …… (i)

Also, $f\left( -3 \right)=6$.

$\Rightarrow a{{\left( -3 \right)}^{2}}+b\left( -3 \right)+c=0$

$\Rightarrow 9a-3b=-6$                                          …… (ii)

Solving the equation (i) and (ii), we obtain

$a=\frac{1}{10}$ and $b=\frac{23}{10}$.

Thus, the required quadratic function is $f\left( x \right)=\frac{1}{10}{{x}^{2}}+\frac{23}{10}x+6$.

31. Find the domain and the range of the function defined by $\mathbf{f}\left( \mathbf{x} \right)=\frac{\mathbf{x}+\mathbf{2}}{\left| \mathbf{x}+\mathbf{2} \right|}$.

Ans. The given function is $f\left( x \right)=\frac{x+2}{\left| x+2 \right|}$.

The function $f\left( x \right)$ is valid if $\left| x+2 \right|\ne 0$.

i.e., if $x+2\ne 0$.

i.e., if $x\ne -2$.

Therefore, the domain of the function is $\mathbb{R}-\left\{ -2 \right\}$.

Now, if $x+2>0$, then $f\left( x \right)=\frac{x+2}{x+2}=1$.

If $x+2<0$, then $f\left( x \right)=\frac{x+2}{-\left( x+2 \right)}=-1$.

Thus, the range of the function $f\left( x \right)$ is $\left\{ -1,1 \right\}$.

32. Find the domain and the range of the function $\mathbf{f}\left( \mathbf{x} \right)=\frac{{{\mathbf{x}}^{\mathbf{2}}}}{\mathbf{1}+{{\mathbf{x}}^{\mathbf{2}}}}$.

Ans.  The given function is $f\left( x \right)=\frac{{{x}^{2}}}{1+{{x}^{2}}}$.

Observe that, $1+{{x}^{2}}\ne 0$. Therefore, the function is defined for all real numbers.

Thus, the domain of the function $f\left( x \right)$ is the set of all real numbers $\mathbb{R}$.

Now, rewrite the given function in terms of $x$, taking $f\left( x \right)=y$.

$y=\frac{{{x}^{2}}}{1+{{x}^{2}}}$

 $\Rightarrow y+{{x}^{2}}y={{x}^{2}} $

 $\Rightarrow {{x}^{2}}\left( 1-y \right)=y $

 $\Rightarrow {{x}^{2}}=\frac{y}{1-y} $

$\Rightarrow x=\sqrt{\frac{y}{1-y}}$, which is valid if $\frac{y}{1-y}\ge 0$, 

i.e., if $y\left( 1-y \right)\ge 0$,

i.e., if $-y\left( y-1 \right)\ge 0$,

i.e., if $y\ge 0$ and $y-1<0$, since $y$ should not be $1$.

i.e., if $0\le y<1$.

Hence, the range of the function $f\left( x \right)$ is $\left[ 0,1 \right)$.

33. If $\mathbf{A}=\left\{ \mathbf{1},\mathbf{2},\mathbf{3} \right\},\,\,\mathbf{B}=\left\{ \mathbf{1},\mathbf{2},\mathbf{3},\mathbf{4} \right\}$, and $\mathbf{R}=\left\{ \left( \mathbf{x},\mathbf{y} \right):\left( \mathbf{x},\mathbf{y} \right)\in \mathbf{A}\times \mathbf{B},\,\mathbf{y}=\mathbf{x}+\mathbf{1} \right\}$, then answer the following questions.

(i) Find $\mathbf{A}\times \mathbf{B}$.

Ans. The given sets are $A=\left\{ 1,2,3 \right\}$ and $B=\left\{ 1,2,3,4 \right\}$.

Then, the cartesian product set,

$A\times B=\left\{ 1,2,3 \right\}\times \left\{ 1,2,3,4 \right\} $

$=\left\{ \left( 1,1 \right),\left( 1,2 \right),\left( 1,3 \right),\left( 1,4 \right),\left( 2,1 \right),\left( 2,2 \right),\left( 2,3 \right),\left( 2,4 \right),\left( 3,1 \right),\left( 3,2 \right),\left( 3,3 \right),\left( 3,4 \right) \right\} $

(ii) Write the domain and range of $\mathbf{R}$.

Ans. The roaster form of the given relation $R=\left\{ \left( x,y \right):\left( x,y \right)\in A\times B,\,\,y=x+1 \right\}$ is given by

$R=\left\{ \left( 1,2 \right),\left( 2,3 \right),\left( 3,4 \right) \right\}$.

Therefore, the domain of the relation $R$ is $\left\{ 1,2,3 \right\}$ and the range of the relation $R$ is $\left\{ 2,3,4 \right\}$.

6 Marks Questions

1. Draw the graphs of the following real function and hence find its range. 

$\mathbf{f}\left( \mathbf{x} \right)=\frac{\mathbf{1}}{\mathbf{x}},\,\,\mathbf{x}\in \mathbf{R},\ \,\mathbf{x}\ne \mathbf{0}$.

Ans.  The provided function is $f\left( x \right)=\frac{1}{x}$, $x\in R$, $x\ne 0$.

Suppose that, $y=f\left( x \right)$. Then the function becomes

$y=\frac{1}{x}$, $x\in R,\,\,x\ne 0$.

Now, consider the following table of values.

Plotting the above table of points into a graph paper and connecting the points by a smooth curve.

From the graph drawn above, it can be concluded that, the curve of the function $f\left( x \right)$ does not pass through the origin.

Thus, the range of the function $f\left( x \right)$ is $\mathbb{R}-\left\{ 0 \right\}$.

2. If $\mathbf{f}\left( \mathbf{x} \right)=\mathbf{x}-\frac{\mathbf{1}}{\mathbf{x}}$, then prove that ${{\left[ \mathbf{f}\left( \mathbf{x} \right) \right]}^{\mathbf{3}}}=\mathbf{f}\left( {{\mathbf{x}}^{\mathbf{3}}} \right)+\mathbf{3f}\left( \frac{\mathbf{1}}{\mathbf{x}} \right)$.

Ans. The given function is $f\left( x \right)=x-\frac{1}{x}$.

Replacing $x$ by $\frac{1}{x}$ into the given function, we obtain

$f\left( \frac{1}{x} \right)=\frac{1}{x}-x$.                                      …… (i)

Therefore, ${{\left[ f\left( x \right) \right]}^{3}}={{\left( x-\frac{1}{x} \right)}^{3}}$

$={{x}^{3}}-\frac{1}{{{x}^{3}}}-3\cdot x\cdot \frac{1}{x}\left( x-\frac{1}{x} \right) $

 $={{x}^{3}}-\frac{1}{{{x}^{3}}}-3\left( x-\frac{1}{x} \right) $

 $={{x}^{3}}-\frac{1}{{{x}^{3}}}+3\left( x-\frac{1}{x} \right) $

$=f\left( {{x}^{3}} \right)+3f\left( \frac{1}{x} \right)$, by applying the equation (i).

3. Draw the graphs of the following real functions and hence find their range.

(i) $\mathbf{f}\left( \mathbf{x} \right)=\mathbf{2x}-\mathbf{1}$

Ans. The provided function is $f\left( x \right)=2x-1$, that is $y=2x-1$, which is a linear equation and so its graph is a straight line. A straight line can be determined using only two points.

So, consider the following table of values.

Now, plot the above points in a graph paper and connect them by a straight line as shown in the following diagram.

By observing the graph drawn above, it is concluded that that $y$ possesses all the real values. Hence, the range of the function $f\left( x \right)$ is the set of all real numbers $\mathbb{R}$. 

(ii) $\mathbf{f}\left( \mathbf{x} \right)=\frac{{{\mathbf{x}}^{\mathbf{2}}}-\mathbf{1}}{\mathbf{x}-\mathbf{1}}$.

Ans. The given function is $f\left( x \right)=\frac{{{x}^{2}}-1}{x-1}$.

It can be written as, $f\left( x \right)=\frac{\left( x+1 \right)\left( x-1 \right)}{x-1}=x+1$, which is a linear equation in $x,y$. So, the graph of the function is a straight line.

A straight line can be determined using only two points.

So, consider the following table of values.

Now, plot the above points in a graph paper and connect them by a straight line as shown in the following diagram.

By observing the graph drawn above, it is concluded that $y$ possesses all the real values except $2$. Hence, the range of the function $f\left( x \right)$ is $\mathbb{R}-\left\{ 2 \right\}$. 

4. Let $\mathbf{f}$ be a function defined by $\mathbf{F}:\mathbf{x}\to \mathbf{5}{{\mathbf{x}}^{\mathbf{2}}}+\mathbf{2}$, $\mathbf{x}\in \mathbf{R}$. Then determine the following results.

(i) Find the image of $\mathbf{3}$ under $\mathbf{f}$.

Ans. The provided function is $f\left( x \right)=5{{x}^{2}}+2$.

Substituting $x=3$, into the given function, we obtain

  $f\left( 3 \right)=5{{\left( 3 \right)}^{2}}+2 $

 $=5\left( 9 \right)+2 $

 $=47. $

Thus, the image of $3$ under $f$ is $47$.

(ii) Find $\mathbf{f}\left( \mathbf{3} \right)\times \mathbf{f}\left( \mathbf{2} \right)$.

Ans. The given function is $f\left( x \right)=5{{x}^{2}}+2$.

Substituting $x=2,3$ successively into the given function, we obtain

 $f\left( 2 \right)=5{{\left( 2 \right)}^{2}}+2 $

 $=5\left( 4 \right)+2 $

 $=22. $

Also,

$f\left( 3 \right)=5{{\left( 3 \right)}^{2}}+2=47$.

Therefore, $f\left( 3 \right)\times f\left( 2 \right)=47\times 22=1034$.

(iii) Find $\mathbf{x}$ such that $\mathbf{f}\left( \mathbf{x} \right)=\mathbf{22}$.

Ans. The given function is $f\left( x \right)=5{{x}^{2}}+2$.

Substituting $f\left( x \right)=22$ into the given function.

$22=5{{x}^{2}}+2$

$\Rightarrow 5{{x}^{2}}=20 $

 $\Rightarrow {{x}^{2}}=4 $

$\Rightarrow x=-2,2$.

The values of $x$ are $-2,$$2$.

5. The function $\mathbf{f}\left( \mathbf{x} \right)=\frac{\mathbf{9x}}{\mathbf{5}}+\mathbf{32}$ is the formula to connect ${{\mathbf{x}}^{\circ }}\mathbf{C}$ to Fahrenheit units. Find the following results.

(i) $\mathbf{f}\left( \mathbf{0} \right)$

Ans. The provided function is $f\left( x \right)=\frac{9x}{5}+32$.

Substituting $x=0$ into the given function, we obtain

$f\left( 0 \right)=\frac{9\left( 0 \right)}{5}+32=32$.

Thus, ${{0}^{\circ }}C={{32}^{\circ }}F$.

(ii) $\mathbf{f}\left( -\mathbf{10} \right)$

Ans. The provided function is $f\left( x \right)=\frac{9x}{5}+32$.

Substituting $x=-10$ into the given function, we get

$f\left( -10 \right)=\frac{9\left( -10 \right)}{5}+32 $

$=-\frac{90}{5}+32 $

$=14 $

Therefore, $-{{10}^{\circ }}C={{14}^{\circ }}F$.

(iii) The value of $\mathbf{x}$ whenever $\mathbf{f}\left( \mathbf{x} \right)=\mathbf{212}$.

Ans. The provided function is $f\left( x \right)=\frac{9x}{5}+32$.

Substituting $f\left( x \right)=212$ into the given function, we get

$212=\frac{9x}{5}+32 $

$\Rightarrow \frac{9x}{5}=212-32 $

$\Rightarrow 9x=5\times \left( 180 \right) $

$\Rightarrow x=100 $

Hence, ${{212}^{\circ }}F={{100}^{\circ }}C$.

6. Find the domain and the range of the following functions:

(i) $\mathbf{f}\left( \mathbf{x} \right)=\sqrt{{{\mathbf{x}}^{\mathbf{2}}}-\mathbf{4}}$

Ans. The provided function $f\left( x \right)=\sqrt{{{x}^{2}}-4}$.

The function $f\left( x \right)$ is valid if ${{x}^{2}}-4\ge 0$.

i.e., if $\left( x+2 \right)\left( x-2 \right)\ge 0$

i.e., if $x\le -2$ or $x\ge 2$.

Therefore, the domain of the function $f\left( x \right)$ is $\left( -\infty ,-2 \right]\cup \left[ 2,\infty  \right)$.

Now, suppose that $y=\sqrt{{{x}^{2}}-4}$.

Since, square root of any real number is always a non-negative real number, so taking square on both sides, yields

${{y}^{2}}={{x}^{2}}-4$

$\Rightarrow {{y}^{2}}+4\ge 0$, since ${{x}^{2}}\ge 0$.

$\Rightarrow {{y}^{2}}\ge -4$, $\forall y\in R$.

Thus, $y\ge 0$, and hence, the range of the function $f\left( x \right)$ is $\left[ 0,\infty  \right)$.

(ii)$\mathbf{f}\left( \mathbf{x} \right)=\sqrt{\mathbf{16}-{{\mathbf{x}}^{\mathbf{2}}}}$.

Ans. The provided function is $f\left( x \right)=\sqrt{16-{{x}^{2}}}$.

The function $f\left( x \right)$ is valid if  $16-{{x}^{2}}\ge 0$,

i.e., if $\left( 4-x \right)\left( 4+x \right)\ge 0$

i.e., if $\left( x-4 \right)\left( x+4 \right)\le 0$

i.e., if $-4\le x\le 4$

Thus, the domain of the function $f\left( x \right)$ is $\left[ -4,4 \right]$.

Now, suppose that $y=\sqrt{16-{{x}^{2}}}$.

Since, square root of any real number is always a non-negative real number, so taking square on both sides of the equation, yields

${{y}^{2}}=16-{{x}^{2}}$

$\Rightarrow {{x}^{2}}=16-{{y}^{2}}$

$\Rightarrow 16-{{y}^{2}}\ge 0$, since ${{x}^{2}}\ge 0$.

$\Rightarrow \left( 4-y \right)\left( 4+y \right)\ge 0$

$\Rightarrow \left( y-4 \right)\left( y+4 \right)\le 0$

$\Rightarrow -4\le y\le 4$.

Again, $y\ge 0$.

Thus, the range of the function $f\left( x \right)$ is $\left[ 0,4 \right]$.

(iii)$\mathbf{f}\left( \mathbf{x} \right)=\frac{\mathbf{1}}{\sqrt{\mathbf{9}-{{\mathbf{x}}^{\mathbf{2}}}}}$.

Ans. The provided function is $f\left( x \right)=\frac{1}{\sqrt{9-{{x}^{2}}}}$.

The function is valid if $9-{{x}^{2}}>0$.

i.e., if $\left( 3-x \right)\left( 3+x \right)>0$

i.e., if $\left( x-3 \right)\left( x+3 \right)<0$

i.e., if $-3<x<3$.

Thus, the domain of the function $f\left( x \right)$ is $\left( -3,3 \right)$.

Now, suppose that, $y=\frac{1}{\sqrt{9-{{x}^{2}}}}$.

Since, the square root of any real number is always a non-negative real number, so taking square on both sides of the equation, yields

${{y}^{2}}=\frac{1}{9-{{x}^{2}}}$

$\Rightarrow 9-{{x}^{2}}=\frac{1}{{{y}^{2}}} $

$\Rightarrow {{x}^{2}}=9-\frac{1}{{{y}^{2}}} $

$\Rightarrow 9-\frac{1}{{{y}^{2}}}\ge 0$, since ${{x}^{2}}\ge 0$.

$\Rightarrow \left( 3-\frac{1}{y} \right)\left( 3+\frac{1}{y} \right)\ge 0$

$\Rightarrow \left( \frac{1}{y}-3 \right)\left( \frac{1}{y}+3 \right)\le 0$

$\Rightarrow y\le -\frac{1}{3}$ or $y\ge \frac{1}{3}$.

Again, since $y>0$, so $y\ge \frac{1}{3}$.

Hence, the range of the function $f\left( x \right)$ is $\left[ \frac{1}{3},\infty  \right)$.

7. Draw the graphs of the following real function and hence find its range: $\mathbf{f}\left( \mathbf{x} \right)={{\mathbf{x}}^{\mathbf{2}}}$.

Ans. The provided function is $f\left( x \right)={{x}^{2}}$.

Since, for all real values of $x$, $f\left( x \right)$ is defined, so the domain of the function is $\mathbb{R}$.

Therefore, let $y={{x}^{2}},\forall x\in \mathbb{R}$.

Now, consider the following table of values.

Now, plotting the above table of points in a clean graph paper by hand and joining these points by a smooth curve. The graph is as shown below.

By observing the graph of the function, we can conclude that, the graph of the function covers only the non-negative region.

Thus, the range of the function $f\left( x \right)$ is $\left[ 0,\infty  \right)$.

8. Define polynomial function. Draw the graph of $\mathbf{f}\left( \mathbf{x} \right)={{\mathbf{x}}^{\mathbf{3}}}$. Find domain and range of the function.

Ans. A function $f:R\to R$ defined as

$f\left( x \right)={{a}_{0}}+{{a}_{1}}x+{{a}_{2}}{{x}^{2}}+\cdot \cdot \cdot +{{a}_{n}}{{x}^{n}}$ , where ${{a}_{0}},{{a}_{1}},{{a}_{2}},...,{{a}_{n}}\in \mathbb{R}$, is said to be a polynomial function of degree $n\in \mathbb{N}\cup \left\{ 0 \right\}$. 

Now, to draw the graph of the function $f\left( x \right)={{x}^{3}}$, consider the following table of values.

So, plotting the above table points in a clean graph paper by hand and connecting those points with a curve, we obtain the graph of the function as given below. 

The domain of the function $f\left( x \right)$ is $\mathbb{R}$.

The range of the function $f\left( x \right)$ is $\mathbb{R}$.

9. (a) If $\mathbf{A},\,\mathbf{B}$ are two sets such that $\mathbf{n}\left( \mathbf{A}\times \mathbf{B} \right)=\mathbf{6}$ and some elements of $\mathbf{A}\times \mathbf{B}$ are $\left( -\mathbf{1},\mathbf{2} \right),\left( \mathbf{2},\mathbf{3} \right),\left( \mathbf{4},\mathbf{3} \right)$, then find $\mathbf{A}\times \mathbf{B}$ and $\mathbf{B}\times \mathbf{A}$.

Ans. The number of the elements in the cartesian product set $A\times B$ is $n\left( A\times B \right)=6$.

Also, it is provided that, some of the elements of $A\times B$ are $\left( -1,2 \right),\left( 2,3 \right)$, and $\left( 4,3 \right)$.

Therefore, $A=\left\{ -1,2,4 \right\}$ and $B=\left\{ 2,3 \right\}$.

Thus, the required sets are

$A\times B=\left\{ \left( -1,2 \right),\left( -1,3 \right),\left( 2,2 \right),\left( 2,3 \right),\left( 4,2 \right),\left( 4,3 \right) \right\}$ and

$B\times A=\left\{ \left( 2,-1 \right),\left( 3,-1 \right),\left( 2,2 \right),\left( 3,2 \right),\left( 2,4 \right),\left( 3,4 \right) \right\}$.

(b) Find domain of the function $\mathbf{f}\left( \mathbf{x} \right)=\frac{\mathbf{1}}{\sqrt{\mathbf{x}+\left[ \mathbf{x} \right]}}$.

Ans. The given function is $f\left( x \right)=\frac{1}{\sqrt{x+\left[ x \right]}}$.

Recall that, the greatest integer function $\left[ x \right]$ is defined as

$\left[ x \right]=\left\{ \begin{align} 0,\,\,\,if\,\,0\le x<1\\ 1,\,\,\,if\,\,\,1\le x<2\\ 2,\,\,\,if\,\,\,2\le x<3\\ ... \end{align} \right.$

Now, $x+\left[ x \right]=\left\{ \begin{align} x+\left[ x \right]>0\,\,\,\,for\text{ all}\,\,\text{x}>\text{0 }\\ 0,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,for\,\,all\,\,x=0\\ x+\left[ x \right]<0\,\,\,for\,\,all\,\,\,x<0\\ \end{align} \right.$

Therefore, the function $f\left( x \right)=\frac{1}{\sqrt{x+\left[ x \right]}}$ is defined for all real values of $x$ such that $x+\left[ x \right]>0$.

Thus, the domain of the function $f\left( x \right)$ is $\left( 0,\infty  \right)$.

Class 11 Maths Chapter 2 Important Questions of Relations and Functions 

Contains the Following Important Topics

• A brief introduction about relations and functions.

• Definition of a cartesian product of sets with examples.

• Definition of a Relations.

• Definition of a Function.

• Range and Domain.

• Representation of a relation.

• Function as a special kind of relation.

• Function as a correspondence.

• Types of relations and definitions.

• Types of functions and definitions.

• Equal functions.

• Real functions.

• The domain of real functions.

• Some standard real functions and their graphs.

• Operations on real functions.

Maths Chapter 2 - Relations and Functions

What is the Relation?

A relation is simply a set or series of ordered pairs. Two components are the x and y coordinates in an ordered pair, generally known as a point.

Example:

What is a Function?

A function on the other hand is a special type of relation since it follows an extra rule. As a relation, a function is also a set of ordered pairs, but only one y-value must be associated with every x-value.

Example:

Domain and Range

The domain refers to a set of input values, while the graph domain includes all of the input values shown on the x-axis. 

The range is the set of output values that are shown on the y-axis.

Example:

In the given relation set Domain is 1, 2, 2, -4 whereas range is 3, 3, 5, 3.

Types of Relations

• Empty Relation

If set A is the empty set, the relation R on a set A is called Empty.

• Full Relation

If A*B, a binary relation R on a set A and B is called full.

• Reflexive Relation

If (a,a)  ∈ R holds a ∈ A.i.e. for each variable, a relationship R is called reflexive on a set A. If A = {a,b} is fixed, then R = {(a,a), (b,b)} is reflexive.

Example:

Consider a set A = {1, 2,}, for instance. Now, R = {(1, 1), (2, 2), (1, 2), (2, 1)} will be the reflexive connection. A relation is therefore reflexive if: (a, a) ∈ R a ∈ A.

• Irreflexive Relation

If (a, a) ∉ R for every a ∉ A, a relationship R on a set A is said to be irreflexive. 

For Example, 

Consider A = {1, 2, 3} and R = {(1, 2), (2, 2), (3, 1), (1, 3)}. As for every a, A, (a, a) ∉ R, i.e., (1, 1) and (3, 3) ∉ R, the relationship R is not reflexive.

• Symmetric Relation

Symmetric relation is a type of binary relation. 

Example 

If RT represents the opposite of R, then R is symmetric if and only if R = RT, a binary relation R over a set X is symmetric.

• Anti-Symmetric Relation

If there is no pair of separate elements of X, each of which is connected by R to the other, the homogeneous relation R on set X is antisymmetric.

• Transitive Relation

If for all elements a, b, c in X, a homogeneous relation R over a set X is transitive when R relates a to b and b to c, then R also relates a to c.

• Equivalence Relation

An equivalence relation is a reflexive, symmetric and transitive binary relation. The relation "is equal to" is the canonical example of a relation of equivalence. A partition of the underlying set into disjoint equivalence classes is given by each equivalence relation.

• Asymmetric Relation

An asymmetric relation is a binary relation R on a set X where (a, b) ∈ X if a is related b then b is not related to a.

Types of Functions

Functions Classified in Terms of Relations:

• Injective or One to One Function

An injective function is a function that maps its domain's distinct elements to its codomain's distinct elements. In other words, each element of the codomain of the function is the image of a maximum of one element of its domain.

• Many to One Function

A Function is called Many to One Function when we have one or the same value as output for two or more real number inputs.

Example:

If we consider f(x)= x2, then if we substitute x with 1, the output will be given as 12 = 1. Similarly, if we substitute x with -1, then we also obtain the output as (-1)2 = 1.

• The Surjective or Onto Function

A function f from a set X to a set Y is surjective if there is at least one element x in the domain X of f for each element y of the codomain Y of f so that f(x) = y.

• Bijective Function

A Bijective function is a function between the two-set elements, in which each element of one set is paired with exactly one element of the other set, and each element of the other set is paired with exactly one element of the first set.

Some Functions in Algebra

• Linear Function

A linear function is a function whose graph is a straight line, that is, degree zero or one polynomial function.

• Quadratic Function

A quadratic function is a polynomial function with one or more variables in which the highest degree term is of the second degree.

• Inverse Function

An inverse function is a function which overturns another function.

Example: 

if the function f applied to the input x gives the result y, then the inverse function g to y gives the result x, i.e. g(y) = x if and only if f(x) = y. The inverse function of f is often denoted as f-1 

• Constant Function

For any input value, a constant function is a function whose value is the same.

Example:

The function x(y) = 1 is a constant function since, irrespective of the input value y, the value of x(y) is 1.

• Identity Function

An Identity function is a function that always returns the same value used as its argument. That is, for f being identity, for all x, the equality f(x)=x holds good.

• Absolute Value Function

An absolute value function is a function which, within absolute value symbols, contains an algebraic expression. 

• Modulus Function

A modulus function is a function which gives a number or variable of an absolute value. It is also defined as a function of absolute value. No matter what feedback has been given to the function, the result of this function is always positive.

• Even Function and Odd Function

Even functions and odd functions are functions that, about taking additive inverses, satisfy unique symmetry relations. In many areas of mathematical analysis, they are important, particularly the power series and Fourier series theory.

• Periodic Function

A periodic function is a function that, at regular intervals, repeats its values.

• Composite Function

A composite function is generally a function within another function. By substituting one function into another one, the composition of a function is carried out. 

fg(x) for instance, is the composite function of f(x) and g(x).

• Signum Function

A signum function is a unique mathematical function that extracts a real number's sign.

How to Decide If a Function is a Relation?

• We can graphically check whether a relation is a function.

• We can analyse the values of x or input.

• The Y of output values may be checked.

• If all the input values are different, then the relation becomes a function, and the relation is not a function if the values are replicated.

Important Study Materials for Class 11 Maths Chapter 2 Relations and Functions  

CBSE Class 11 Maths Chapter-wise Important Questions

CBSE Class 11 Maths Chapter-wise Important Questions and Answers cover topics from all 14 chapters, helping students prepare thoroughly by focusing on key topics for easier revision.

Important Related Links for CBSE Class 11 Maths