Revision Notes on Thermal Properties of Matter for NEET 2023

Heat

• Heat is a type of thermal energy that flows from a higher temperature body to a lower temperature body when they come into contact.

• A body's heat, or thermal energy, is the sum of all of its constituent particles' kinetic energies due to translational, vibrational, and rotational motion.

• We know that Joule (J) is the SI unit of heat energy.

• The calorie is the most common unit of heat energy. We know that,  $1\text{cal}=4.18~\text{J}$

• A calorie is the amount of heat required to raise the temperature of $1~\text{g}$ of water by ${{1}^{{}^\circ }}\text{C}$.

• We know that, mechanical energy or work (W) can be converted into heat (Q) by $1~\text{W}=\text{JQ}$

• Here J = Joule's mechanical equivalent of heat. $\text{J}$ is a conversion factor (not a physical quantity) and its value is $4.186~\text{J}/\text{cal}$.

Temperature

• The degree of hotness or coldness of a body is referred to as its temperature. A thermometer is a device that is used to measure the temperature.

• We know that, highest possible temperature achieved in the laboratory is about 108 K while the lowest possible temperature attained is $10^{-8}\,K$.

• Cryogenics is a branch of physics concerned with the production and measurement of temperatures below 0 degrees Celsius, whereas pyrometer is concerned with the measurement of extremely high temperatures. The sun's core temperature is 107 degrees Fahrenheit, while its surface temperature is 600 degrees Fahrenheit.

• NTP or STP implies $273.15~\text{K}\left( {{0}^{{}^\circ }}\text{C}={{32}^{{}^\circ }}\text{F} \right)$.

Different Scale of Temperature

• Celsius Scale: In Celsius scale of temperature, the melting point of ice is taken as ${{0}^{{}^\circ }}\text{C}$ &${{100}^{{}^\circ }}\text{C}$ as the boiling point of water & space between these two points is divided into 100 equal parts.

• Fahrenheit Scale: In Fahrenheit scale of temperature, the melting point of ice is taken as ${{32}^{{}^\circ }}\text{F}$ & 211 $^{{}^\circ }\text{F}$ as the boiling point of water & the space between these two points is divided into 180 equal parts.

• Kelvin scale: In Kelvin scale of temperature, the melting point of ice is taken as $273~\text{K}$ & $373~\text{K}$ as the boiling point of water & the space between these two points is divided into 100 equal parts.

Relation Between Different Scales of Temperatures

• $\dfrac{C}{100}=\dfrac{F-32}{180}=\dfrac{K-273}{100}=\dfrac{R}{80}$, Where C stands for Centigrade scale, F for Fahrenheit scale and R for Reamer scale.

Measurement of Temperature

A thermometer is used to measure temperature. The liquids that are frequently utilised in liquid-in glass thermometers are Mercury and Alcohol.

• Two fixed points must be picked as reference points while building a thermometer. Freezing (ice point) and boiling point are the names of these fixed points (steam point). At these two locations, water freezes and boils under normal pressure.

• The ice and steam points on the Fahrenheit Temperature Scale are $32^{\circ} \mathrm{F}$ and $212^{\circ} \mathrm{F}$, respectively.

Absolute Zero

• The lowest energy state for a thermodynamic system is absolute zero. In terms of temperature, it is equivalent to 459.67 °F in Fahrenheit and 273.15 °C in Celsius. temperature gradations. Related Articles: absolute temperature scale for temperature energy with no points.

• Experimentally, it is discovered that the lowest temperature is $273.15^{\circ} \mathrm{C}$, which is also referred to as absolute zero.

• The relation between the temperature in kelvin and in Celsius scale is given by$\mathrm{T}=\mathrm{t}_{\mathrm{C}}+273.15$

Thermal stress:

• When a rod is held between two stiff supports and allowed to expand or contract as the temperature changes, the rigid support prevents the rod from expanding or contracting. The rod is then stressed, which is known as thermal stress. Thermal expansion (if the rod were free), $\Delta L=\alpha \cdot L \cdot \Delta \theta$

• Thus, thermal stress $=\operatorname{strain} \times Y=\left(\dfrac{\Delta L}{L}\right) Y=\alpha Y(\Delta \theta)$

Thermal Expansion

The phenomenon of thermal expansion is when a body's dimensions grow as its temperature rises.

The Reason why Thermal Expansion Happens is:-

Any heated object looks to have expanded because, as particles begin to move randomly when heated, the average distance between molecules also increases. As shown in the image below, atoms are closely packed, but when heat is applied, they begin to move erratically.

Types of Thermal Expansion

• Linear Expansion: The expansion in length 

• Area Expansion: The expansion in area 

• Volume Expansion: The expansion in volume

Linear Expansion

Heat causes a change in length known as linear expansion. the following is the linear expansion formula:

$\dfrac{\Delta L}{L_{o}}=\alpha_{L} \Delta T$

Where,

$L_o$ = original length,

$L=$ expanded length,

$\alpha=$ length expansion coefficient,

$\Delta T=$ temperature difference,

$\Delta \mathrm{L}=$ change in length

Volume Expansion

Volume expansion is the result of a temperature-related change in volume. This is the volume expansion formula:

$\dfrac{\Delta V}{V_{o}}=\alpha_{V} \Delta T$

Where,

$V_o$ = original volume,

$V=$ expanded volume,

$a v=$ volume expansion coefficient,

$\Delta \mathrm{T}=$ temperature difference,

$\Delta V=$ change in volume after expansion

Area Expansion

The change in area brought on by a temperature shift is known as area expansion. The area-expansion formula is as follows:

$\dfrac{\Delta A}{A_{o}}=\alpha_{A} \Delta T$

Where,

$A=$ original area,

$\Delta \mathrm{A}=$ change in the area,

$\vartriangle{\alpha_{A}}=$ area expansion coefficient,

$\Delta T=$ temperature difference,

Principle of Calorimetry:

Heat passes from the hot object to the cold object when two things of different temperatures come into touch. Heat lost by the hot object is equal to heat acquired by the cool object if the system is sufficiently thermally separated from its surroundings.

Strain: 

• We know that, Change in dimension/original dimension.

• Strain is dimensionless and unit less quantity.

• Modulus of Elasticity $=\dfrac{\text{ Stress }}{\text{ Strain }}$

Strain is of Three Types

• Longitudinal Strain: Longitudinal strain is defined as the change in length per unit of original length. We know that formula, Longitudinal strain $=\dfrac{\Delta L}{L}$

• Volume Strain: It refers to the change in volume per unit of original volume. Volume strain $=\dfrac{\Delta V}{V}$

• Shearing Strain: When a body's shape changes without changing its volume, the strain produced is known as shearing strain, and it is defined as the angle through which a plane perpendicular to the cubical body's fixed surface turns under the influence of tangential force.

• Shearing strain, $\mathrm{S}=a \tan \theta$ for small angles, $\tan \theta=\theta$

• $\Rightarrow \mathrm{S}=a \theta$

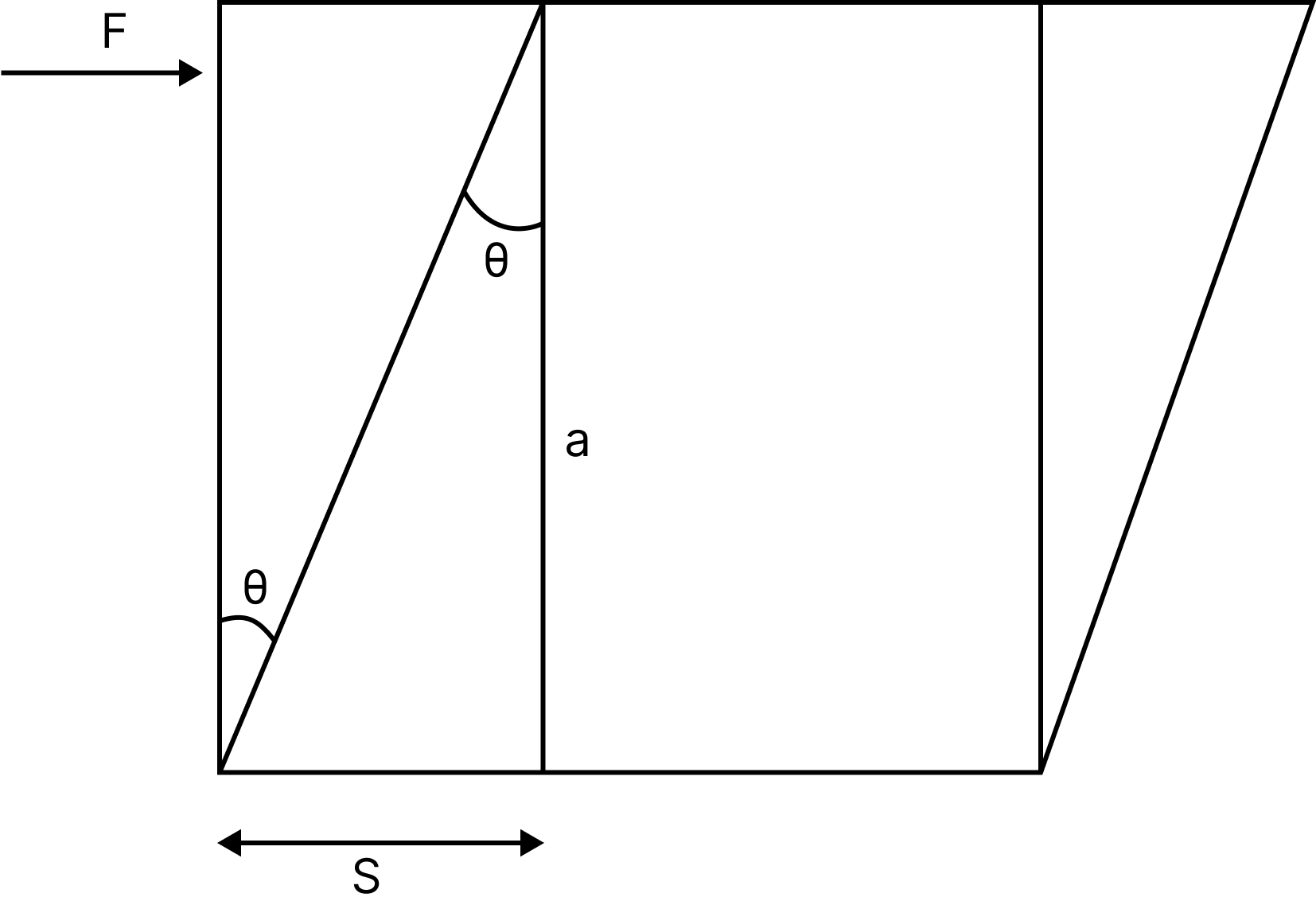
Shearing strain

• The greater the modulus of elasticity, the more stress is developed, and thus the greater the restoring force.

Anomalous Behaviour of Water

• Water exhibits some unusual behaviour in that it contracts rather than expands when heated at $0^{\circ} \mathrm{C}$ and continues to do so until it reaches $4^{\circ} \mathrm{C}$. Given a quantity of water, its density is maximal since the volume is minimal at $4^{\circ} \mathrm{C}$. Water begins to expand after  $4^{\circ}C$. The volume grows as the $4^{\circ} \mathrm{C}$  lowers, which causes the density to decrease. This indicates that water has its greatest density at $4^{\circ} \mathrm{C}$.

• Advantages of Anomalous behaviour of Water: Because of this property of water, lakes and ponds only freeze at the top layer of the water column and do not freeze at the bottom. However, if the water froze at the bottom as well, then it would be impossible for animal and plant life to exist.

Thermometric Property:

A thermometric property is a property of an object that changes with temperature. Thermometers are the tools used to measure temperature.

Below are listed some thermometric characteristics and thermometers.

• Gas thermometers with constant volume have thermometric properties.

• Metals with electrical resistance

• Capillary tube housing a mercury column.

(I)Pressure of a Gas at Constant Volume

$\dfrac{{{p}_{1}}}{{{T}_{1}}}\text{ }=\dfrac{{{p}_{2}}}{{{T}_{2}}}$

${{p}_{t}}\text{ }={{p}_{0}}\left( 1+\dfrac{t}{273} \right)$

$t\text{ }={{\left( \dfrac{{{p}_{t}}-{{p}_{0}}}{{{p}_{100}}-{{p}_{0}}}\times 100 \right)}^{{}^\circ }}\text{C}$

Here,$p,{{p}_{100}}$ & ${{p}_{t}}$ are pressure of a gas at constant volume ${{0}^{{}^\circ }}\text{C},{{100}^{{}^\circ }}\text{C}$ and${{t}^{{}^\circ }}\text{C}$.

A constant volume gas thermometer can measure temperature from $-{{200}^{{}^\circ }}\text{C}$ to${{500}^{{}^\circ }}\text{C}$.

Hooke's Law

• According to Hooke’s law within the elastic limit, the amount of stress developed in the body is proportional to the amount of strain produced in the body.

• Stress $\propto$ Strain

$\Rightarrow $ Stress $=E\times $ Strain

Here, $E$ is modulus of elasticity

• We know that, There are three types of modulus of elasticity

• Within the elastic limit, Young's modulus of elasticity ($Y$) is defined as the ratio of normal stress to longitudinal strain.

Hence, $Y=\dfrac{\text{ normal stress }}{\text{ longitudinal strain }}=\dfrac{F/A}{\Delta L/L}=\dfrac{F\cdot L}{\pi {{r}^{2}}\Delta L}=\dfrac{MgL}{\pi {{r}^{2}}\Delta L}$

• Bulk modulus of elasticity $(K)$ within the elastic limit is defined as the ratio of normal stress to the volumetric strain.

Hence, $K=\dfrac{\text{ normal stress }}{\text{ volumetric strain }}=-\dfrac{F/A}{\Delta V/V}=\dfrac{pV}{\Delta V}[\because F/A=p]$

• Modulus of rigidity or shear modulus of elasticity ( $\eta $ ) within the elastic limit is defined as the ratio of tangential stress to the shearing strain.

Hence, $\eta =\dfrac{\text{ tangential stress }}{\text{ shearing strain }}=\dfrac{F/A}{\theta }=\dfrac{FL}{Ax}$

Poisson's Ratio

• When a deforming force is applied to the free end of a suspended wire with length $l$and radius\[R\], the length of the wire increases by \[dl\]but the radius decreases by\[dR\].

• Thus, a single force produces two types of strain: longitudinal and lateral strain.

• Poisson's ratio is the proportion of lateral and longitudinal strains.

• Poisson's ratio $(\sigma )$ is given by

$\sigma =\dfrac{\text{ Lateral strain }}{\text{ Longitudinal strain }}=-\dfrac{\Delta R/R}{\Delta L/L}=-\dfrac{\Delta R}{R}\times \dfrac{L}{\Delta L}$

• Here, the negative sign indicates that as the wire's length increases, the radius decreases.

• Poisson's ratio is a dimensionless quantity with no units.

• We know that, Theoretical value of$\sigma $ lies between $-1$ and $+\dfrac{1}{2}$.

• We know that, Practical value of $\sigma $ lies between 0 and $+\dfrac{1}{2}$.

• Relation between Elastic Constants $Y,K,\eta$ and $\sigma $

• $\dfrac{9}{Y}=\dfrac{1}{K}+\dfrac{3}{\eta }$

• $\eta =\dfrac{Y}{2(1+\sigma )}$

• $K=\dfrac{4}{3(1-2\sigma )}$           

• $\sigma =\dfrac{3K-2\eta }{2\eta +6K}$

(II)Electrical Resistance of Metals

${{R}_{t}}={{R}_{0}}\left( 1+at+\beta {{t}^{2}} \right)$

• Here  $\alpha $ and $\beta $ are constants for a metal.

• Then $\beta $ is too small therefore we can take

${{R}_{t}}={{R}_{0}}(1+at)$

• Here, $\alpha =$ temperature coefficient of resistance and ${{R}_{0}}$ & ${{R}_{{{t}^{\prime }}}}$ are electrical resistances at ${{0}^{{}^\circ }}\text{C}$ &${{t}^{{}^\circ }}\text{C}$.

$\alpha =\dfrac{{{R}_{2}}-{{R}_{1}}}{{{R}_{1}}{{t}_{2}}-{{R}_{2}}{{t}_{1}}}$

Here ${{R}_{1}}$ & ${{R}_{2}}$ are electrical resistances at temperatures ${{t}_{1}}$ & ${{t}_{2}}$.

• $t=\dfrac{{{R}_{t}}-{{R}_{0}}}{{{R}_{100}}-{{R}_{0}}}\times {{100}^{{}^\circ }}\text{C}$

Here ${{R}_{100}}$ is the resistance at${{100}^{{}^\circ }}\text{C}$.

• We know that, Platinum resistance thermometer can measure temperature from $-{{200}^{{}^\circ }}\text{C}$ to${{1200}^{{}^\circ }}\text{C}$.

(III) Length of Mercury Column in a Capillary Tube

${{I}_{t}}={{I}_{0}}(1+\alpha t)$

• Here $\alpha =$ coefficient of linear expansion and ${{I}_{0}},{{I}_{t}}$ are lengths of mercury column at ${{0}^{{}^\circ }}\text{C}$ &${{t}^{{}^\circ }}\text{C}$.

Thermo Electro Motive Force

• When two thermocouple junctions are kept at different temperatures, a thermo-emf is created between them, which varies with the temperature difference between them.

• Thermo-emf

$E=at+b{{t}^{2}}$

• Here $a$ and $b$ are constants for the pair of metals.

• We know that the temperature of hot junction when cold junction is at ${{0}^{{}^\circ }}\text{C}$.

$t={{\left( \dfrac{{{E}_{t}}}{{{E}_{100}}}\times 100 \right)}^{{}^\circ }}\text{C}$

• Here ${{E}_{100}}$ is the thermo-emf when the hot junction is at${{100}^{{}^\circ }}\text{C}$.

• We know that, A thermo-couple thermometer can measure temperature from $-{{200}^{{}^\circ }}\text{C}$ to${{1600}^{{}^\circ }}\text{C}$.

Thermal Equilibrium

• The bodies are said to be in thermal equilibrium when there is no heat transfer between them when they are in contact.

Triple Point of Water:

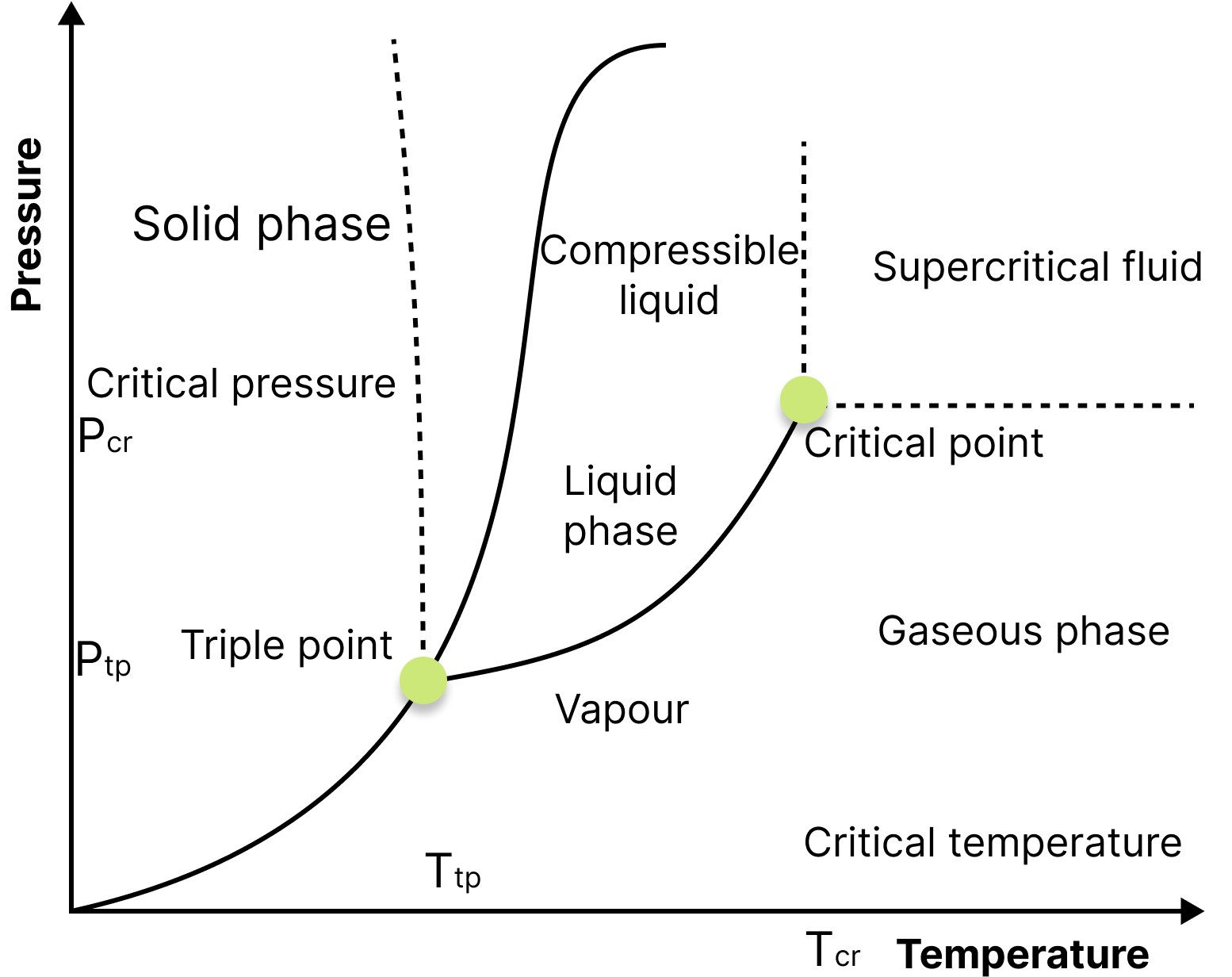
Triple Point

• The triple point of water is defined as the pressure and temperature at which water coexists in equilibrium in all three states of matter, namely ice, water, and vapour.

• The triple point of pure water is at 0.01°C (273.16K, 32.01°F) and 4.58 mm (611.2Pa) of mercury and is used to calibrate thermometers.

Specific Heat

• The specific heat of a substance is the amount of heat required to raise the temperature of a unit mass of the substance.

• Specific heat can be denoted by c or s.

• Specific heat SI unit is joule/kilogram- $^{{}^\circ }{{\text{C}}^{\prime }}\left( J/\text{kg}{{-}^{{}^\circ }}\text{C} \right)$. Specific heat dimensions are$\left[ {{\text{L}}^{2}}~{{\text{T}}^{-2}}\theta -1 \right]$.

• We know that, the specific heat of water is $4200~\text{J}~\text{k}{{\text{g}}^{-10}}{{\text{C}}^{-1}}$ or$1\text{cal}{{\text{g}}^{-1}}{{\text{C}}^{-1}}$, which high compared with most other substances.

Gases Have Two Types of Specific Heat

• At constant volume, the specific heat capacity$\left( {{C}_{v}} \right)$.

• At constant pressure, the specific heat capacity (C).

• We know that, Specific heat at constant pressure $\left( {{C}_{p}} \right)$ is greater than specific heat constant volume$\left( {{C}_{v}} \right)$, i.e., ${{C}_{p}}>{{C}_{v}}$.

• For molar specific heats we can write  ${{C}_{p}}-{{C}_{v}}=R$

• Here $R=$ gas constant and this relation are called Mayer's formula.

• The ratio of a gas's two main specific heats is denoted by$\gamma $.

$\gamma =\dfrac{{{C}_{p}}}{{{C}_{V}}}$

• We know that the value of $\gamma $ depends on the atomicity of the gas.

• The ratio of a gas's two primary specific heats is written as $Q=mc\Delta t$, Here, m= mass of the substance, $c=$specific heat of the substance and $\Delta \text{t}=$ change in temperature.

Thermal (Heat) Capacity

• A body's heat capacity is equal to the amount of heat energy required to raise its temperature through${{1}^{{}^\circ }}\text{C}$.

• We know that, Heat capacity = $mc\Delta T$

• Here $c=$ specific heat of the substance of the body and $m=$ mass of the body.

• Heat capacity SI unit is joule/kelvin$(\text{J}/\text{K})$.

Water Equivalent

• It is the amount of water whose thermal capacity is equal to the body's heat capacity. It is represented by the letter W.

• Then we know that, $\text{W}=\text{ms}=$ Heat capacity of the body.

Latent Heat

• Latent heat is the heat energy absorbed or released at constant temperature per unit mass for state change.

• The heat energy absorbed or released during a state change is given by $\text{Q}=\text{mL}$

• Here $\text{m}=$ mass of the substance and $\text{L}=$ latent heat.

• Latent heat unit is \[cal/g\] or $J/kg$ and its dimension is$\left[ {{M}^{0}}{{L}^{2}}{{T}^{-2}} \right]$.

• For water at its normal boiling point or condensation temperature $\left( {{100}^{{}^\circ }}\text{C} \right)$, the latent heat of evaporation is $L=540\text{cal}/\text{g}$$=40.8~\text{kJ}/\text{mol}$ $=2260~\text{kJ}/\text{kg}$

• For water at its normal freezing or melting point $\left( {{0}^{{}^\circ }}\text{C} \right)$, the latent heat of fusion is $\text{L}=80\text{cal}/\text{g}=60~\text{kJ}/\text{mol}$$=336~\text{kJ}/\text{kg}$

• It is more painful to get burnt by steam rather than by boiling was ${{100}^{{}^\circ }}\text{C}$ gets converted to water at${{100}^{{}^\circ }}\text{C}$, then it gives out 536 $\text{cal}/\text{gm}$heat. So, it is clear that steam at ${{100}^{{}^\circ }}\text{C}$ has more heat than wat ${{100}^{{}^\circ }}\text{C}$ (i.e., boiling of water).

• When snow falls, the temperature of the atmosphere drops dramatically because the snow absorbs heat from the atmosphere. So, when snow falls in the mountains, one does not feel too cold, but when ice melts, he feels too cold.

• Ice cream has a stronger shivering effect on teeth than water (obtained from ice). This is because ice cream absorbs a lot of heat from your teeth when you eat it.

Melting

• Melting is the process of converting a solid into a liquid at a constant temperature.

Evaporation

• Evaporation is the conversion of liquid into vapour at any temperature (even below the boiling point).

Boiling

• When a liquid is gradually heated, at a certain temperature, the saturated vapour pressure of the liquid equals atmospheric pressure, and bubbles of vapour rise to the liquid's surface. This is referred to as liquid boiling.

• The boiling point of a liquid is the temperature at which it begins to boil. The boiling point of water increases as pressure increases and decreases as pressure decreases.

Sublimation

• Sublimation is the process of converting a solid into a vapour.

Hoar Frost

• Hoar frost refers to the transformation of vapours into solids.

Calorimetry

• This is the branch of heat transfer concerned with measuring heat. Calories or kilocalories are commonly used to measure heat.

Principle of Calorimetry

• When a hot body and a cold body are mixed, the heat lost by the hot body equals the heat gained by the cold body.

• Heat lost = Heat gain

Expansion of Solids

• There are three types of expansion that occur in solids.

• Linear expansion is the term used to describe the expansion of length as a result of heating.

• We know that, Increase in length ${{I}_{2}}={{I}_{1}}(1+\alpha \Delta t)$

• Here, ${{I}_{1}}$ and ${{I}_{2}}$ are initial and final lengths, $\Delta \text{t}=$ change in temperature and $\alpha =$ coefficient of linear expansion.

• We know that, Coefficient of linear expansion $\alpha =\left( \dfrac{\Delta l}{l}\times \Delta t \right)$

• Here $l=$ real length and $\Delta l=$ change in length and $\Delta \text{t}=$ change in temperature.

Superficial Expansion: 

• The term "superficial expansion" refers to the expansion of an area as a result of heating.

• We know that, Increase in area ${{\text{A}}_{2}}={{\text{A}}_{1}}(1+\beta \Delta \text{t})$

• Here, ${{A}_{1}}$ and ${{A}_{2}}$ are initial and final areas and $\beta $ is a coefficient of superficial expansion.

• We know that, Coefficient of superficial expansion $\beta =\left( \dfrac{\Delta A}{A}\times \Delta t \right)$

• Here, $\text{A}=$ Area, $\Delta \text{A}=$ change in area and $\Delta \text{t}=$ change in temperature.

Cubical Expansion:

• Cubical expansion refers to the expansion of volume as a result of heating.

• We know that, Increase in volume ${{V}_{2}}={{V}_{1}}(1+\gamma \Delta t)$

• Here ${{V}_{1}}$ and ${{V}_{2}}$ are initial and final volumes and $\gamma $ is a coefficient of cubical expansion.

• We know that, Coefficient of cubical expansion $\gamma =\dfrac{\Delta V}{V\times \Delta t}$

• Here $V=$ real volume, $\Delta V=$ change in volume and $\Delta t=$ change in temperature. Relation between coefficients of linear, superficial and cubical expansions $\beta =2\alpha $ and $\gamma =3\alpha $ Or $\alpha :\beta :\gamma =1:2:3$

Expansion of Liquids

• Only volume expansion occurs in liquids when heated.

1. Apparent Expansion of Liquids: When the expansion of a container    containing liquid on heating is not taken into account, the observed expansion is referred to as apparent expansion of liquids.

• We know that, Coefficient of apparent expansion of a liquid $\left( {{\gamma }_{a}} \right)=\dfrac{\text{ apparent increase in volume }}{\text{ original volume }\times \text{ rise in temperature }}$

2. Actual Expansion of Liquids: When the expansion of the container containing the liquid on heating is considered, the observed expansion is referred to as real expansion of liquids.

• We know that, Coefficient of real expansion of a liquid

$\left( {{\gamma }_{r}} \right)=\dfrac{\text{ real increase in volume }}{\text{ original volume }\times \text{ rise in temperature }}$

• Here, Both, ${{\gamma }_{r}}$, and ${{\gamma }_{\text{a}}}$ are measured in $^{{}^\circ }{{\text{C}}^{-1}}$.

• We can show that ${{\gamma }_{r}}={{\gamma }_{\text{a}}}+{{\gamma }_{g}}$

• Here, ${{\gamma }_{r}}$ and ${{\gamma }_{\text{a}}}$ are coefficient of real and apparent expansion of liquids and ${{\gamma }_{\text{g}}}$ is coefficient of cubical expansion of the container.

Anomalous Expansion of Water

• If temperature of water is increased from${{0}^{{}^\circ }}\text{C}$, then its volume decreases up to${{4}^{{}^\circ }}\text{C}$, becomes minimum at ${{4}^{{}^\circ }}\text{C}$ and then increases. The behaviour of water around ${{4}^{{}^\circ }}\text{C}$ is called anomalous expansion of water.

Expansion of Gases

• In gases, there are two types of coefficients of expansion.

1. Volume Coefficient (${{\gamma }_{V}}$): The change in volume per unit volume per degree Celsius at constant pressure is known as the volume coefficient.

${{\gamma }_{V}}=\dfrac{{{V}_{2}}-{{V}_{1}}}{{{V}_{0}}\left( {{t}_{2}}-{{t}_{1}} \right)}$

Here${{\text{V}}_{0}},~{{\text{V}}_{1}}$, and ${{\text{V}}_{2}}$ are volumes of the gas at ${{0}^{{}^\circ }}\text{C},{{\text{t}}_{1}}^{{}^\circ }\text{C}$ & ${{\text{t}}_{2}}^{{}^\circ }\text{C}$.

2. Pressure Coefficient$\left( {{\text{y}}_{\text{p}}} \right)$: The change in pressure per unit pressure per degree Celsius at constant volume is referred to as the pressure coefficient.

${{\gamma }_{p}}=\dfrac{{{p}_{2}}-{{p}_{1}}}{{{p}_{0}}\left( {{t}_{2}}-{{t}_{1}} \right)}$

Here  ${{p}_{0}},{{p}_{1}}$ and ${{p}_{2}}$ are pressure of the gas at ${{0}^{{}^\circ }}\text{C},{{t}_{1}}^{{}^\circ }\text{C}$ and ${{t}_{2}}^{{}^\circ }\text{C}$.

Practical Applications of Expansion

• Space is left between the ends of two rails when rails are laid down on the ground.

• The transmission cables are loosely attached to the poles.

• The iron rim that goes on a cart wheel is always slightly smaller in diameter than the wheel itself.

• A glass stopper stuck in the neck of a glass bottle can be removed by warming the bottle's neck.

Important Points

• A pendulum clock becomes slow and loses time in the summer due to an increase in its time period.

• We know that, Loss of time in a time period $\Delta T=(1/2)a\Delta \theta T$.  The loss of time in any given time interval t can be expressed as $\Delta T=(1/2)\alpha \Delta \theta t$

• At higher temperatures, a scale will expand and scale readings will be lower than true values, resulting in

True value = scale reading $(1+\alpha \Delta t)$

Here, $\Delta $t is the temperature difference.

• However, at lower temperatures, the reading will be higher or the true value will be lower.

Thermal Conductivity:

The capacity of a material to carry or transport heat is known as thermal conductivity. It is frequently represented by the sign "$k$" or "$\lambda$." Thermal resistivity is the name given to these physical quantities reciprocal.  High thermal conductivity materials are employed in heat sinks, while low $\lambda$ values materials are used as thermal insulators.

$\mathrm{K}=(\mathrm{QL}) /(\mathrm{A} \Delta \mathrm{T})$

Where,

• $\mathrm{K}$ is the thermal conductivity in $\mathrm{W} / \mathrm{m} \cdot \mathrm{K}$

• $\mathrm{Q}$ is the amount of heat transferred through the material in Joules/second or Watts

• $\mathrm{L}$ is the distance between the two isothermal planes

• $A$ is the area of the surface in square metres

• $\Delta T$ is the difference in temperature in Kelvin

Thermal Resistance:

Thermal resistance is a property of heat and a measurement of the difference in temperature at which a substance or object resists the flow of heat. The reciprocal of thermal conductance is thermal resistance.

Thermal resistance $=\dfrac{\mathrm{L}}{(\mathrm{kA})}$, measured in $\mathrm{KW}^{-1}$

$\mathrm{L}$ is the length of the material (measured on a path parallel to the heat flow) $(\mathrm{m})$ $\mathrm{k}$ is the thermal conductivity of the material $(\mathrm{W} /(\mathrm{Km}))$

A is the cross-sectional area (perpendicular to the path of heat flow) $\left(\mathrm{m}^{2}\right)$

Newton's Law of Cooling:

Newton's law of cooling states that the rate of heat loss from a body is inversely related to the temperature difference between the body and its surroundings.

Newton's law of cooling is given by, $\mathrm{dT} / \mathrm{dt}=\mathrm{k}\left(\mathrm{T}_{\mathrm{t}}-\mathrm{T}_{\mathrm{s}}\right)$

Here,  $T_{t}=$ temperature of the body at time $t$ and $T_{s}=$ temperature of the surrounding, $k=$ Positive constant that is dependent on the size and kind of the body surface being studied.

Stefan Boltzmann Law:

The radiation radiated from an area A of a black body at absolute temperature T is directly proportional to the fourth power of the temperature, according to Stefan Boltzmann's law.

$E=\sigma T^{4}$, the Greek letter sigma ( $\sigma$ ) representing the constant of proportionality, called the Stefan-Boltzmann constant. This constant has the value $5.670374419 \times 10^{-8}$ watt per metre ${ }^{2}$ per $\mathrm{K}^{4}$. 

Formula Chart:

1. Specific heat capacity$\text{ s}=\dfrac{\text{Q}}{\text{m}\Delta \theta }$

unit $\to \text{J}/\text{kg}{{-}^{{}^\circ }}\text{C}($ S. I. system)

$\to \text{cal}/\text{g}{{\text{m}}^{-}}^{{}^\circ }\text{C}$

2. Heat capacity (C)$\text{ C}=\text{ms}=\dfrac{\text{Q}}{\Delta \theta }$

3. Water equivalent $\text{ W}=\text{ms}$

4. Latent heat

(a) The heat required to change the unit mass of a solid to its liquid state at its melting point is called Latent Heat of Fusion. For changing from ice to water ${{L}_{f}}=80\text{cal}/\text{gm}$.

(b) The heat required to change the unit mass of the liquid to its vapour state at its boiling points is called Latent Heat of Evaporation. For changing from water to steam${{L}_{v}}=540\text{cal}/\text{gm}$.

(c) $Q=mL$

5. Principle of calorimetry

Heat released by I substance $\Rightarrow $ Heat absorbed by II substance

${{\text{m}}_{1}}~{{\text{s}}_{1}}\left( ~{{\text{T}}_{1}}-\text{T} \right)={{\text{m}}_{2}}~{{\text{s}}_{2}}\left( T-{{\text{T}}_{1}} \right)$

Final temp $T=\dfrac{{{m}_{1}}{{s}_{1}}{{T}_{1}}+{{m}_{2}}{{s}_{2}}{{T}_{2}}}{{{m}_{1}}{{s}_{1}}+{{m}_{2}}{{s}_{2}}}$

6. Solution technique to find specific heat of a solid ${{S}^{\prime }}=\dfrac{\left( {{m}_{1}}+W \right)s\left( \theta -{{\theta }_{1}} \right)}{{{m}_{2}}\left( {{\theta }_{2}}-\theta  \right)}$

7. To find the latent heat of vaporisation $L=\dfrac{\left( {{m}_{1}}+W \right)s\left( \theta -{{\theta }_{1}} \right)}{{{m}_{2}}}-s\left( {{\theta }_{2}}-\theta  \right)$

8. Mechanical equivalent of heat (J)

$\text{W}=\text{JH}$ Unit of $\text{J}=$ Joule/cal.

$1J=4.2~\text{J}/\text{cal}.$

In joule In calorie

9. Conversion of temp. scale

$\dfrac{{{\text{T}}_{\text{C}}}-0}{100}=\dfrac{{{\text{T}}_{\text{F}}}-32}{180}=\dfrac{{{\text{T}}_{\text{R}}}-0}{80}=\dfrac{{{\text{T}}_{\text{K}}}-273}{100}$

$\Rightarrow \dfrac{{{T}_{C}}}{5}=\dfrac{{{T}_{{{F}^{-}}}}-32}{9}=\dfrac{{{T}_{R}}}{4}=\dfrac{{{T}_{{{K}^{K}}}}-273}{5}$

$\dfrac{\Delta {{\text{T}}_{C}}}{5}=\dfrac{\Delta {{\text{T}}_{\text{F}}}}{9}=\dfrac{\Delta {{\text{T}}_{\text{R}}}}{4}=\dfrac{\Delta {{\text{T}}_{\text{K}}}}{5}$

$\Delta \to $ change

${{\text{T}}_{\text{C}}}\to $ Temp.in Celsius

${{\text{T}}_{\text{F}}}\to $ Temp.in Fahrenheit

${{\text{T}}_{\text{R}}}\to $ Temp.in Reaumer

${{\text{T}}_{\text{K}}}\to $ Temp.in Kelvin

10. Relationship between Fahrenheit and Celsius Temperature:

$F=\dfrac{9}{5} C+32$

$F:$ Fahrenheit temperature

C: Celsius Temperature

11. Stress $=\dfrac{\text{ force }}{\text{ Area }}=\dfrac{F}{A}$

12. Longitudinal $\operatorname{strain}=\dfrac{\Delta l}{l}$

13. Volumetric strain $=\dfrac{\Delta V}{V}$

14. Shearing strain $=\phi =\dfrac{x}{L}$

15. Hooke’s Law: $\dfrac{\text{ stress }}{\text{ strain }}=E$

16. Linear expansion:

$\dfrac{\Delta L}{L_{0}}=a_{L} \Delta T$

$L=L_{0}\left(1+a_{L} \Delta T\right)$

17. Volume expansion:

$\dfrac{\Delta V}{V_{o}}=V_{V} \Delta T$

$V=V_{o}\left(1+Y_{v} \Delta T\right)$

18. Young Modulus$=Y=\dfrac{\text{ Normal stress }}{\text{ longitudinal strain }}=Y=\dfrac{F/A}{\Delta l/L}$

19. Modulus of Rigidity (Shear modulus) $=G=\dfrac{\text{ Tangential stress }}{\text{ shearing strain }}=G=\dfrac{F}{A\phi }$

Example 1: A spherical black body with a radius of $12 \mathrm{~cm}$ radiates 450 -watt power at $500 \mathrm{~K}$. If the radius were halved and the temperature doubled, the power radiated in watts would be:

1. 225

2. 450

3. 1000

4. 1800

Answer: (D)

Explanation:

We know that radiation from the body is given as $\mathrm{E}=\epsilon \sigma \mathrm{AT}^{4}$

$\dfrac{\mathrm{E}_{1}}{\mathrm{E}_{2}}=\dfrac{\mathrm{r}_{1}^{2} \times \mathrm{T}_{1}^{4}}{\mathrm{r}_{2}^{2} \times \mathrm{T}_{2}^{4}}=\dfrac{0.12^{2} \times 500^{4}}{0.06^{2} \times 1000^{4}} $

$\mathrm{E}_{2}=\dfrac{450 \times 0.06^{2} \times 1000^{4}}{0.12^{2} \times 500^{4}}=1800 \mathrm{watt}$

Hence, the power radiated in watts would be 1800 watt.

Example 2:Two identical bodies are made of a material for which the heat capacity increases with temperature. One of these is at $100^{\circ} \mathrm{C}$, while the other one is at 0 . If the two bodies are brought into contact, then assuming no heat loss, the final common temperature is -

1. $50^{\circ} C$

2. more than $50^{\circ} \mathrm{C}$

3. less than $50^{\circ} \mathrm{C}$ but greater than $0^{\circ} \mathrm{C}$

4. $0_{0} C$

Answer: (B)

Explanation:

If $\theta$ be the final common temperature.

Further, let $s_{c}$ and $s_{h}$ be the average heat capacities of the cold and hot (initially) bodies respectively (where $s_{c}<s_{h}$ given)

From, principle of calorimetry,

heat lost = heat gained

$s_{\mathrm{h}}\left(100^{\circ} \mathrm{C}-\theta\right)=\mathrm{s}_{\mathrm{c}} \theta $

$\Rightarrow \theta \dfrac{s_{\mathrm{h}}}{s_{\mathrm{h}}+s_{\mathrm{c}}} \times 100^{\circ} \mathrm{C} =\dfrac{100^{\circ} \mathrm{C}}{1+\dfrac{s_{c}}{s_{\mathrm{h}}}}$

$1+\dfrac{s_{\mathrm{c}}}{s_{\mathrm{h}}}<2\left(\because \dfrac{s_{\mathrm{c}}}{s_{\mathrm{h}}}<1\right)$

$\therefore \theta>\dfrac{100^{\circ} \mathrm{C}}{2} \text { or } \theta>50^{\circ} \mathrm{C}$

Hence, the final common temperature will be more than $50^{\circ} \mathrm{C}$.

Importance of Thermal Properties of Matter

This chapter is very important in the Class 11 Physics syllabus as it introduces the concept of thermal energy. It also explains what heat is and how it propagates in an object. The fundamental principles of propagation of heat are explained in this chapter. It will help students to understand why the rate of propagation of heat varies among different substances.

This chapter will proceed to explain what heat is, how it can be measured, and how it can be correlated to thermal energy. Students will learn that the cumulative outcome of rotational, vibration and translational energies constitute thermal energy.

This chapter will also help students to create a conceptual foundation related to thermodynamics. It will also explain what absolute zero temperature is and how it can bring the chaotic particles of a substance to rest. All molecular motions cease to exist.

The expansion of solids, liquids, and gases will be explained well in the Thermal Properties of Matter notes. Students will find out the mathematical derivations for calculating the expansion and contraction of solids.

Students will also learn that work done is directly proportional to energy disappearing from the system. This theory will proceed to derive the work-heat relation and specific heat capacity of objects.

Benefits of Vedantu’s Thermal Properties of Matter NEET Notes

• These revision notes are compiled by the experts to offer a simpler version of the concepts mentioned in this chapter. The easier explanation of scientific terms of this chapter will enable you to complete preparing this chapter and revise it faster before an exam.

• The format of these notes has been simplified too so that NEET aspirants like you can easily locate the fundamental principles, derivations, laws, and formulas of this chapter at a glance. It will help you to reduce the time of your revision sessions.

• Recalling these concepts will become much easier during the exam when you refer to these notes. The organized format of these notes will help you to recall the formulas to solve questions and score more in the exam.

Download Thermal Properties of Matter Notes PDF

Get the free PDF version of these notes and make your preparation for this chapter complete. Use the Thermal Properties of Matter Class 11 NEET notes whenever you want to develop a strong conceptual foundation. Refer to the notes for doubt clearance and focus on the fundamental principles only and prepare the Physics syllabus for NEET perfectly.

Important Related Links for NEET