Revision Notes on Moving Charges and Magnetism for NEET 2023

Electromagnetics:

• Magnetic effects of electric current is a branch of physics that studies the influence of a magnetic field produced by a current or moving charge.

Magnetic Field:

• It is a region or place where the magnetic effect of a magnet, current carrying conductor, or moving charge can be felt.

•  The tesla is the SI unit for it (T).

Biot-Savart Law:

• According to this law, the magnetic flux density of which dB, is directly proportional to the length of the element dl, the current I, is given by

$dB=\dfrac{{{\mu }_{0}}}{4\pi }\dfrac{idl\sin \theta }{{{r}^{2}}}~\text{Wb}/{{\text{m}}^{2}}$ or tesla

Biot-Savart Law

• $dB=\dfrac{{{\mu }_{0}}}{4\pi }\dfrac{id\mathbb{I}\times \mathbf{r}}{{{r}^{3}}}$

Here, ${{\mu }_{0}}$ is a constant and it is called the permeability of free space and it is given as,

${{\mu }_{0}}=4\pi \times {{10}^{-7}}~\text{Wb}/\text{A}-\text{m}$

Applications of Biot-Savart's Law

• Biot-Savart law is used to calculate magnetic responses even at the atomic or molecular level.

• Biot-Savart law is used in aerodynamic theory to calculate the velocity induced by vortex lines.

Importance of Biot-Savart Law

• Coulomb's law is similar to Biot-Savart law in electrostatics.

• Biot-Savart law is also applicable for very small conductors carrying current.

• Biot-Savart law is applicable for symmetrical current distribution.

Rules to Find the Direction of Magnetic Field:

• Right Hand Palm Rule: The direction of the field will be perpendicular to the palm if we spread our right hand in such a way that the thumb is facing the direction of current and the fingers are facing the spot where we need to identify the direction of the field.

• Maxwell's Right Handed Screw Rule: When the tip of a right-handed corkscrew moves in the direction of current flow through the conductor, the rotation of the screw's head gives the direction of magnetic lines of force.

Ampere's Circuital Law:

• Ampere's Circuital Law states that the line integral of the magnetic field around any closed path in vacuum is equal to ${{\mu }_{0}}$ times the total current enclosed by the loop.

             $\oint{\mathbf{B}}\cdot d\mathbf{1}={{\mu }_{0}}{{I}_{\text{net }}}$

• The simplified form of it is $B={{\mu }_{0}}{{I}_{\text{net }}}$, this equation is used in the following conditions.

• At every point of the closed circuit $B\|dl$.

• The magnetic field in the closed circuit is uniform at all points.

Ampere's Law states that the magnetic field generated by an electric current is proportional to the size of the electric current.

Gauss's law states that the electric flux through any closed surface is equal to the total charge inside divided by ${{\varepsilon }_{0}}$. Charges are the source and sinks of the electric field.

Biot-Savart's law states that the magnetic intensity at any point along an infinitely long straight wire caused by a constant current is exactly proportional to the current and inversely proportional to the distance between point and wire.

According to this, coulomb's law states that the amount of the electrostatic force of attraction between two point charges is directly proportional to the product of the charges' magnitudes and inversely proportional to the square of the distance between them formula.

$F=\dfrac{k{{q}_{1}}{{q}_{2}}}{{{d}^{2}}}$

Application of Ampere's Circuital Law:

• The following are the principal applications of Ampere's circuital law:

• The magnetic field produced by an infinitely long straight wire

$B=\dfrac{{{\mu }_{0}}}{2\pi }\cdot \dfrac{I}{r}$

• The magnetic field due to conducting rod of radius $R$ at a point at distance $r$ from the rod

$r<R,\,B=\left( \dfrac{{{\mu }_{o}}I}{2\pi {{R}^{2}}} \right)\cdot r$

or $B\propto r$

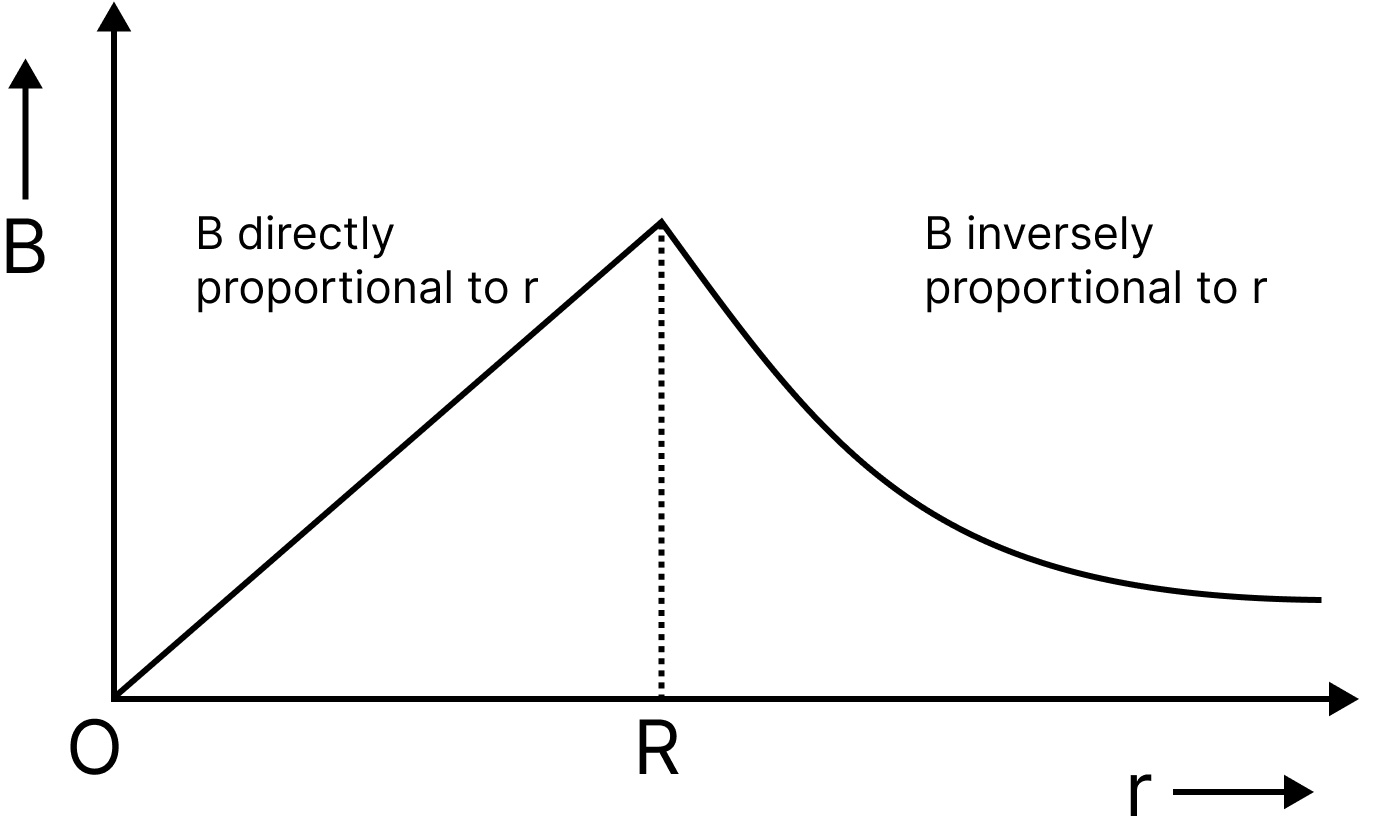
The Magnetic Field Due to Conducting Rod

$B=\dfrac{{{\mu }_{0}}I}{2\pi R}(c)$ r>R

$B=\dfrac{{{\mu }_{0}}}{2\pi }\cdot \dfrac{I}{r}$

The magnetic field due to hollow cylindrical pipe of radius $R$ at a point at distance $r$ from the current carrying hollow pipe.

1. If $r<R$, then $B=0$

2. If $r\ge R$, then $B=\dfrac{{{\mu }_{0}}}{2\pi }\cdot \dfrac{I}{r}$

Force Between Two Parallel Current Carrying Conductor:

• Two parallel linear conductors carrying currents in the same direction attract one another, while oppositely repelling each other.

• As a result, the force between two parallel current-carrying conductors per unit length is

$F=\dfrac{{{\mu }_{0}}}{4\pi }\cdot \dfrac{2{{I}_{1}}{{I}_{2}}}{d}$

Magnetic Field of a Moving Point Charge:

• The magnetic field due to a charge $q$, moving with speed $v$ at a point $P$ at a distance $r$ from the charge is given by the following formula.

$\vec{B}=\dfrac{{{\mu }_{0}}}{4\pi }\cdot \dfrac{q}{{{r}^{2}}}(\vec{v}\times \vec{r})$

Force on a Moving Charge in Magnetic Field:

• In a magnetic field, the force on a moving charge is given by

${{F}_{m}}=qvB\sin \theta =q(\mathbf{v}\times \mathbf{B})$
where,  $v=$ magnitude of charge,
$B=$ intensity of charge, and

$\quad \theta =$ angle between direction of velocity and direction of magnetic field

• Lorentz force is another name for it.
• Neutral and big substances are affected by electromagnetic and gravitational forces.
• The kinetic energy of a moving charge that moves perpendicular to the magnetic field remains constant.
• The force that acts simultaneously in the presence of an electric and magnetic field. $F=q(E+v\times B)$

Rules to Find the Direction of Force:

• The palm rule for the right hand: The fingertips of a linear conductor clasped in the palm of the right hand with the thumb pointing in the direction of the current will point in the direction of lines of force.

• The rule of Fleming's left hand: If we spread our left hand's forefinger, middle finger, and thumb in such a way that they are perpendicular to each other, the first forefinger will represent the magnetic field, the second central finger will represent the current, and the thumb will represent the force.

Motion of Charged Particle in a Magnetic Field:

• A charged particle goes in a circular route when it enters a magnetic field perpendicularly.

• Radius of circular path, $r=\dfrac{mv}{Bq}=\dfrac{\sqrt{2m{{E}_{K}}}}{qB}$.

• Time period of particle, $T=\dfrac{2\pi m}{Bq}$.

• Frequency of particle, $n=\dfrac{Bq}{2\pi m}$.

• When a charged particle moves in the direction of a magnetic field, it is not subjected to any force.

•  The velocity of a proton travelling through a magnetic field constantly changes.

Force on a Current Carrying Conductor in Magnetic Field:

• When a current-carrying conductor is put in a magnetic field, it is subjected to a force, which is provided by

${{F}_{m}}=\text{ Bil }\sin \theta =i\mathbf{l}\times \mathbf{B}$.
Here , $B=$ intensity of magnetic field,
$i=$ current in the conductor, $l=$ length of the conductor and
$\theta =$ the angle the current makes with the magnetic field

• If, $\theta ={{90}^{{}^\circ }}$ or $\sin \theta =1$, then $F=ilB$ (Maximum)

• If , $\theta =0$ or $\sin \theta =0$

• $F=ilB\times 0=0$ The acting force is 0 when the current carrying conductor is parallel to the field.

Application of Current Carrying Conductor:

• We know that, Magnetic force acting on a current carrying conductor is not the central force because the $F=BIdl\sin \theta $ expression does not depend upon $r$.

• The force d F is always perpendicular to $B$ and idl.

Magnet

• Lodestone, a naturally occurring black-colored material, can attract iron items maintained nearby.

• In early days, the Greeks observed this property of loadstone an oxide called magnetite$\left( \text{F}{{\text{e}}_{3}}{{\text{O}}_{4}} \right)$. This type of substance is called magnet.

Magnet is of Two Types:

• Natural Magnet: Natural magnets are substances found in nature that attract small bits of iron, known as magnetism.

• Artificial Magnets: Artificial magnets are magnets that have been created artificially. It has a set shape and size. For example, Horseshoe magnet

Important Facts Related to Magnet

• The life of an artificial magnet is short, whereas the life of a natural magnet is long.

• The earth's magnetism lasts an endless amount of time.

• An induced magnet is an unstable magnet.

• Magnets can be found in electric bells, fans, and washing machines, among other things.

Pole Strength

• We know that the ability of magnetic poles to attract magnetic material is known as pole strength. It is denoted by $m$. The pole strength of the North and South pole is represented by $+m$ and $-m$.

• Pole strength $(m)=\dfrac{\text{ Magnetic force }}{\text{ Magnetic induction }}=\dfrac{F}{m}$

• Ampere-metre or Newton/Tesla is the unit of pole strength.

Magnetic Axis

• The magnetic axis is the line that connects a magnet's north and south poles.

Effective Length of Magnet

• The effective length of a magnet is defined as the distance between the North Pole and the South Pole.

Magnetic Dipole

• A magnetic dipole is a magnetic north and south poles separated by a short distance.

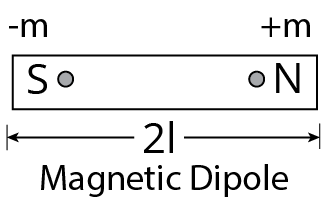
Magnetic Dipole

Magnetic Moment

• A bar magnet's magnetic moment is equal to the product of its length and pole strength. $M$ symbolises it. $M=(2l)\times m$

• Unit of magnetic moment is ampere-metre$^{2}$.

Magnetic Field

• A magnetic field is the area surrounding a magnet in which another magnet exerts a force on it.

Magnetic Field Lines

• Magnetic field lines are imaginary lines that depict the direction of a magnetic field.Some properties of magnetic field lines are given below.

• Magnetic line of force always from closed curves.

• They leave the North Pole and enter the South Pole externally.

• They move from the South Pole to the North Pole within the magnet.

• They tend to contract laterally.

• The magnetic field lines never intersect each other.

Some Properties of Magnet

• Intensity of Magnetization: It is defined as magnetic moment per unit volume. i.e. $I=\dfrac{M}{V}$, Where, $M=$ magnetic dipole moment, and $V=$ volume of material.

• Magnetic Permeability: The magnetic permeability of a material is the measure of degree to which the magnetic field can penetrate or permeate a medium. It is denoted by $\mu $ is $\mu =\dfrac{B}{H}$. Where, $B=$ magnetic induction and $H=$ magnetising field.

• Magnetic susceptibility the intensity of magnetization per unit magnetising field is known as magnetic susceptibility i.e. $\phi =\dfrac{I}{H}$ where, $I=$ intensity of magnetization and $H=$ magnetising field.

• Relation between magnetic susceptibility and permeability the relative magnetic permeability, 

${{\mu }_{r}}=1+\phi $

Where, ${{\mu }_{r}}=\dfrac{\mu }{{{\mu }_{0}}}$. (${{\mu }_{0}}$=absolute permeability)

$\therefore \quad \dfrac{\mu }{{{\mu }_{0}}}=1+\phi \quad \text{ or }\quad \mu ={{\mu }_{0}}(1+\phi )$

Torque on Bar Magnet in Magnetic Field:

Torque on Bar Magnet in Magnetic Field

• In figure, a uniform magnetic field $B$ is represented by an equidistant parallel line. NS is a bar magnet of length $2l$ and the strength of each pole is $m$. 

• The magnet is held at angle $\theta $ with the direction of $B$ Torque$(\tau )=mBl\sin \theta +mBl\sin \theta $

$\tau =2mBl\sin \theta =MB\sin \theta $

          In vector, $\tau =\vec{M}\times \vec{B}$

Work Done in Rotating a Dipole in a Magnetic Field:

• The total work done in deflecting the dipole through an angle $\theta $ from ${{0}^{{}^\circ }}$ is $W=MB(1-\cos \theta )$

• If $\theta ={{0}^{{}^\circ }}$, then $W=MB[1-1]=0$

• If $\theta ={{90}^{{}^\circ }}$, then $W=MB$

• If $\theta ={{180}^{{}^\circ }}$, then $W=2MB$, Where, $M$ is magnetic dipole moment.

Field due to Small Bar Magnet (Magnetic Dipole)

• In end on position (on axial point) $B=\dfrac{{{\mu }_{0}}}{4\pi }\dfrac{2M}{{{r}^{3}}}$ Here, $r$ is distance of the required point from the centre of dipole.

• In broad side on position (on perpendicular bisector) $B=\dfrac{{{\mu }_{0}}}{4\pi }\dfrac{M}{{{r}^{3}}}$.

• At any general point$(r,\theta )$ relative to center of dipole $B=\dfrac{{{\mu }_{0}}}{4\pi }\dfrac{M}{{{r}^{3}}}\sqrt{1+3{{\cos }^{2}}\theta }$.

Hall Effect: 

• According to the Hall Effect concept, a voltage can be measured at a right angle to the current route when a current-carrying conductor or semiconductor is exposed to a perpendicular magnetic field. The Hall Effect is the process through which a voltage can be measured.

• A current begins to flow when a conductive plate is connected to a circuit with a battery. From one end of the plate to the other, the charge carriers will move in a straight line. Magnetic fields are created as a result of charge carrier motion. The magnetic field of the charge carriers is altered when a magnet is brought close to the plate. The charge carriers' direct passage is disrupted as a result. The Lorentz force is the force that alters the direction in which charge carriers flow.

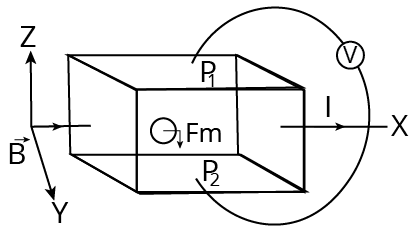
Hall Effect

We can use the Hall Effect to: 

• Determine the sign of charge carriers inside the conductor.

• Determine the number of charge carriers per volume unit.

• The Hall voltage represented as $\mathrm{V}_{\mathrm{H}} \ the \ formula \ gives $

Hall voltage $V_{H}=\dfrac{B w j}{n e}$

Moving Coil Galvanometer

• Torque exerts its influence on a current-carrying coil suspended in a uniform magnetic field. As a result, the coil rotates. As a result, the deflection of a moving coil galvanometer's coil is directly proportional to the current flowing in the coil.

• It is made up of a rectangular coil wound with many turns of thinly insulated copper wire over a light metallic frame. A fine phosphor-bronze strip from a movable torsion head suspends the coil between the pole pieces of a horseshoe magnet. The coil's lower end is connected to a phosphor bronze hairspring with a few turns.

• The spring's other end is attached to a binding screw. A soft iron cylinder is symmetrically placed inside the coil. The hemispherical magnetic poles generate a radial magnetic field in which the plane of the coil is always parallel to the magnetic field. To measure the deflection of the coil, a small plane mirror attached to the suspension wire is used in conjunction with a lamp and scale arrangement.

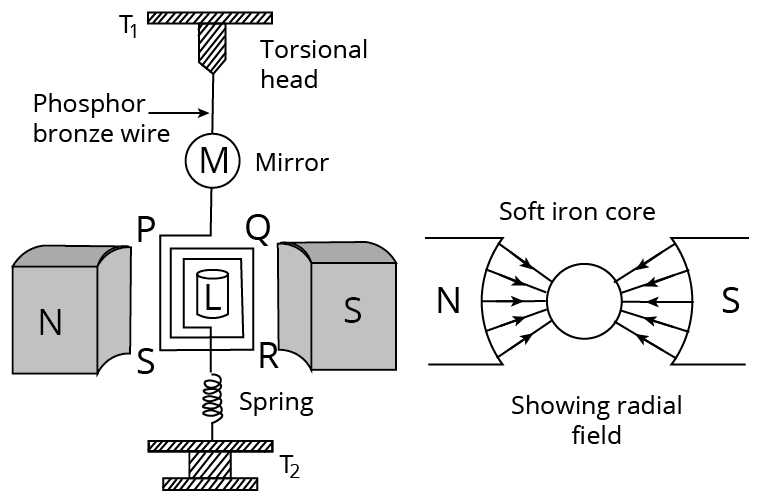
Galvanometer

• According to Fleming's left-hand rule, we can see that the forces on AD and BC are pointing in opposite directions. When equal and opposite forces F, known as the couple, act on the coil, a torque is produced. The coil deflects as a result of this torque.

• Torque = force x perpendicular distance between forces, as we know.

$\tau \text{ }=\text{ }F\text{ }\times ~b$

Using the value of F that we already know,

Torque acting on the coil's single-loop ABCD $=\text{ }BIl~\times ~b$

Here $l\times ~b~$ is the area A of the coil,

As a result, the torque acting on the coil n turns is given by

$\tau \text{ }=\text{ }nIAB$

The resulting magnetic torque causes the coil to rotate and the phosphor bronze strip to twist. In turn, the spring S connected to the coil generates a counter torque or restoring torque k, resulting in a constant angular deflection.

Under Equilibrium Condition:

• $k\theta \text{ }=\text{ }nIAB$ in this case, k is referred to as the spring's torsional constant (restoring a couple per unit twist). The twist or deflection is measured as the value indicated on a scale by a pointer connected to the suspension wire.

$\theta =\text{ }\left( \text{ }nAB\text{ }/\text{ }k \right)I$

Thus  $\theta \propto I$

For a given galvanometer, the quantity $nAB\text{ }/\text{ }k$ is a constant. As a result, the deflection of the galvanometer is directly proportional to the current that flows through it.

Important Formula:

Example 1: A steady current I flows along an infinitely long hollow cylindrical conductor of radius R. This cylinder is placed coaxially inside an infinite solenoid of radius 2R. The solenoid has n turns per unit length and carries a steady current I. Consider a point P at a distance r from the common axis. The correct statement(s) is(are)

(A) In the region $0<r<R$, the magnetic field is non-zero.

(B) The magnetic field is along the common axis in the region $R<r<2 R$.

(c)In the region $R<r<2 R$, the magnetic field is tangential to the circle of radius $r$, centred on the axis.

(D) In the region $r>2 R$, the magnetic field is non-zero.

Ans: A and D

Hint: Magnetic field is a vector field that explains the magnetic influence on moving charges, currents, and magnetic materials. A moving charge in a magnetic field is subjected to a force perpendicular to its own velocity and the magnetic field.

Complete solution:

We know that

(i) For a cylinder, $B=0$ for $0<r<R$ and $B=\dfrac{\mu_{0}}{4 \pi} \times \dfrac{2 I}{r}$ for $r>R$.

(ii) For a solenoid, $B=\mu_{0} n$ for $0<r<R$ and $B=0$ for $r>R$.

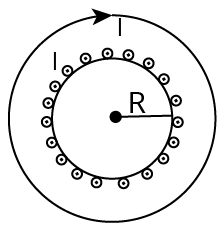
Magnetic Field Induction for Solenoid

Assuming that the magnetic induction to be $B_{C}$ for the cylinder and $B_{S}$ for solenoid.

In the region $\mathrm{R}>\mathrm{r}>0, \mathrm{~B}_{\mathrm{S}}=\mu_{0}$ nI while $\mathrm{B}_{\mathrm{C}}=0$. Therefore, the total field is non-zero.

Hence, option (A) is correct.

In the region $2 R<r<R$, the magnetic field is not along the axis of cylinder which is given as

$B=\sqrt{B_{S}^{2}+B_{C}^{2}}$

Hence, option (B) is wrong.

For checking option (C), in the region $R<r<2 R$, the magnetic field is tangential to the circle of radius $\mathrm{r}$, centred on the axis. So this statement is wrong because the magnetic field is not in the plane of the circle.

Hence, option (C) is wrong.

In the region $\mathrm{r}>2, \mathrm{~B}_{\mathrm{S}}=0$; while $B_{C}=\dfrac{\mu_{0}}{4 \pi} \times \dfrac{2 I}{r}$. Therefore the total field is non-zero.

Hence, option (D) is correct.

Example 2: If a charged particle (+q) is projected with certain velocity parallel to the magnetic field, then it will 

 (a) Trace helical path

(b) Trace circular path

(c) Continue its motion without any change

(d) Come to rest instantly

Ans: C

Hint: Lorentz force, the force exerted on a charged particle q travelling with velocity v through an electric and magnetic field E and B. The Lorentz force refers to the total electromagnetic force F acting on the charged particle.

Complete solution:

Lorentz's force acting on a charged particle is known as Lorentz force, and it is expressed as $\vec{F}=q[\vec{E}-\vec{v}\times \vec{B}]$

Net Force acting on charge $=F$

The electric field exerts a force on the charge $=\text{qE}$

Force acting on the charge due to magnetic field $=qv\times B$ or qvBsin$\theta $

Here $\theta $ is the angle between the direction of the magnetic field and direction of motion of a particle

According to question given that if a charged particle (+q) is projected with certain velocity parallel to the magnetic which means that angle between the direction of magnetic field $\theta $ and direction of motion of a particle is ${{0}^{{}^\circ }}$

And force acting Force acting on charge due to magnetic field $={{F}_{\text{magnetic }}}=+qvB\sin \left( {{0}^{{}^\circ }} \right)$

$\therefore {{F}_{\text{magnetic }}}={{0}^{{}^\circ }}$

As a result, there is no net force acting on the charged particle (+) moving parallel to the magnetic field, and it will continue to move in the same direction.

Importance of Class 12 Physics NEET Moving Charges and Magnetism

The chapter Moving Charges and Magnetism explains how an electric charge will behave in presence of a magnetic field. It will also explain that an electric circuit emits a magnetic field. The effect of current flowing through a conductor has a magnetic field.

The advanced concepts of moving charges and the production of a magnetic field will be explained in this chapter. Students will be able to correlate the laws, the formulae and the laws they have studied in the earlier classes. Every law and term related to this conceptual topic of electricity will be explained using mathematical expressions and equations.

You will learn how to calculate the magnetic field of a conductor carrying a current. It will explain the intensity and features of this magnetic field at different positions. With the help of the Moving Charges and Magnetism notes, you will be able to find the correlation between different types of electric circuits and their magnetic fields.

The explanation of the laws is very important for your NEET preparation. Your concepts related to this chapter will become clear and you can solve the questions without any hassle. The principles related to the current flowing in a solenoid or a straight conductor can be differentiated easily after finishing preparing this chapter.

Benefits of Vedantu’s Moving Charges and Magnetism Class 12 Notes

• These notes have been compiled to deliver the simplest explanation of all the concepts, laws, derivations, and correlations of the terms. It will become a lot easier for you to find the consolidated knowledge related to this chapter in these notes.

• These notes can be downloaded for free and used according to your study sessions. You can refer to the notes whenever you are facing any doubt. Resolve your queries and proceed to complete preparing this chapter faster. Learn how the experts have described these crucial concepts related to moving charges and find out the best ways to answer fundamental NEET questions.

• Evaluate your preparation level by solving the sample questions given in these notes. Check the solutions given by the experts to develop your answering skills and score well in the main exam.

Download Moving Charges and Magnetism Class 12 Notes PDF for NEET

Get the free downloadable version of the Moving Charges and Magnetism NEET notes PDF and add it to your study material. Make your revision sessions more productive by checking the simpler explanations. Cover this chapter faster by using the organised format of the Moving Charges and Magnetism notes for NEET and recall what you have studied easily. Make yourself more efficient in comprehending the objective of conceptual questions asked in the NEET exam to score more.

Important Related Links for NEET