NCERT Solutions For Class 8 Maths Chapter 4 Data Handling Exercise 4.1 - 2025-26
FAQs on NCERT Solutions For Class 8 Maths Chapter 4 Data Handling Exercise 4.1 - 2025-26
1. Where can I find accurate and step-by-step NCERT Solutions for Class 8 Maths Chapter 4, Data Handling, for the 2025-26 session?
You can find detailed and reliable NCERT Solutions for Class 8 Maths Chapter 4 (Data Handling) right here on Vedantu. Our solutions are crafted by subject matter experts to provide a clear, step-by-step methodology for solving every problem in the textbook, ensuring alignment with the latest CBSE 2025-26 curriculum guidelines.
2. What is the correct method to create a frequency distribution table for ungrouped data as per the NCERT Class 8 Maths solutions?
The correct method for creating a frequency distribution table, as demonstrated in the NCERT solutions, involves these steps:
- First, create a table with three columns: the data item (observation), tally marks, and frequency (the count).
- Go through the raw data one by one and make a tally mark ('|') against the corresponding data item.
- To make counting easier, group the tally marks in sets of five (the fifth mark crosses the previous four).
- Finally, count the tally marks for each data item to get its frequency and write the number in the frequency column.
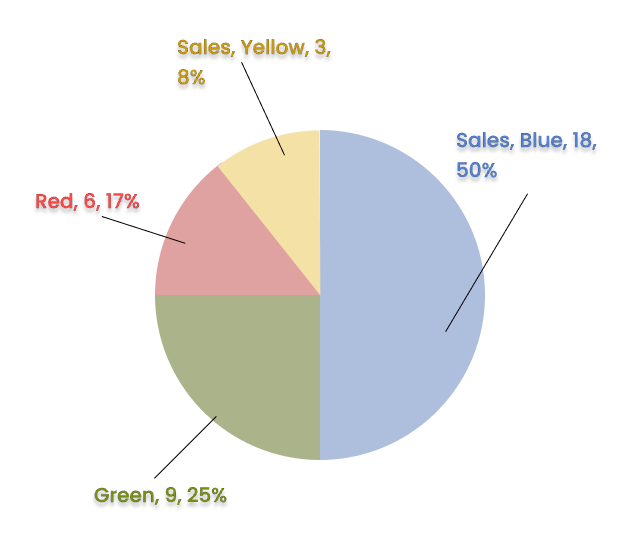
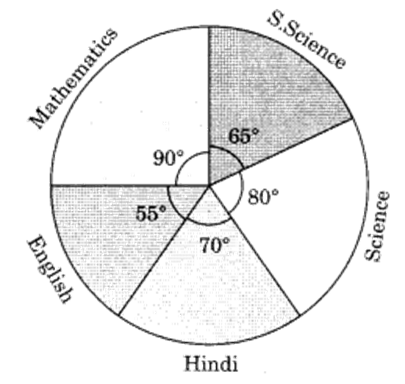
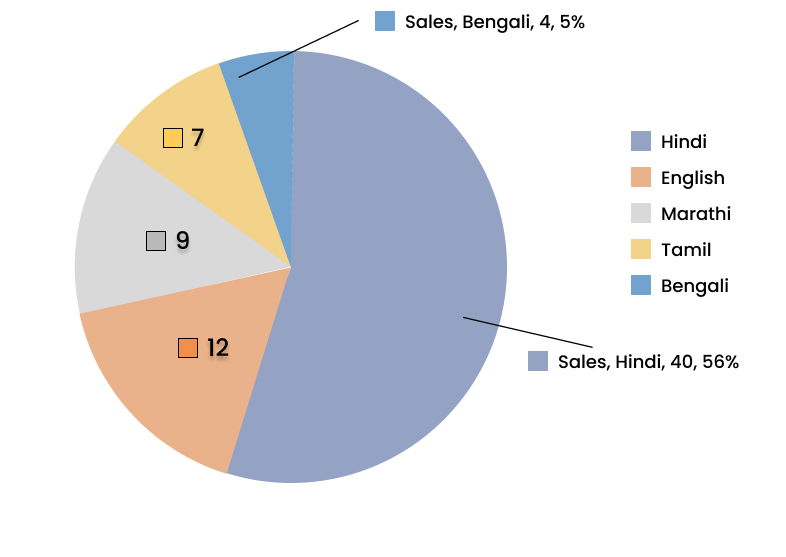
3. How do the NCERT Solutions for Chapter 4 explain the step-by-step process of constructing a pie chart?
The NCERT Solutions for Chapter 4 break down the construction of a pie chart into clear steps:
- Calculate the fraction or percentage that each category represents out of the total.
- Find the central angle for each category by multiplying its fraction by 360°. The formula is: (Value of the component / Total value) × 360°.
- Draw a circle of a convenient radius.
- Use a protractor to draw sectors corresponding to the calculated central angles for each category.
- Label each sector clearly to represent the data accurately.
4. Why do the NCERT Solutions for Chapter 4 recommend using a histogram instead of a bar graph for continuous data?
The NCERT Solutions implicitly guide us to use a histogram for continuous data (grouped in class intervals) because a histogram visually represents the continuous nature of the data. Unlike a bar graph, which has gaps between bars for discrete categories, a histogram has no gaps between its bars. This signifies that the data flows from one class interval to the next without a break, which is the correct way to represent a continuous frequency distribution.
5. What is the standard approach to solving problems involving probability in NCERT Class 8 Maths Chapter 4?
The standard approach to solving probability problems, as per the NCERT solutions, is to use the fundamental probability formula. The steps are:
- First, identify the total number of possible outcomes in the experiment. This will be the denominator.
- Next, determine the number of favourable outcomes for the specific event you are interested in. This will be the numerator.
- Finally, calculate the probability using the formula: P(Event) = (Number of Favourable Outcomes) / (Total Number of Possible Outcomes).
6. How does following the Vedantu NCERT Solutions for Data Handling help in avoiding common mistakes in exams?
Following our NCERT Solutions helps you avoid common mistakes by emphasising the correct methodology. For example, students often get confused between using a bar graph and a histogram. The solutions clarify this by applying the correct graph for the given data type. They also provide a structured format for creating tables and calculating angles for pie charts, which reduces calculation errors and ensures you present your answers exactly as per the CBSE pattern, securing full marks.
7. When solving questions from Exercise 4.1, how do the solutions demonstrate the importance of organising raw data first?
The solutions for Exercise 4.1 consistently demonstrate that organising raw data into a frequency distribution table is the crucial first step. By doing this, the data becomes structured and easy to interpret. This organised format makes it simpler to answer subsequent questions about the frequency of specific items, identify patterns, or prepare the data for creating graphs. The solutions show that without this initial organisation, analysing the data would be chaotic and prone to errors.
8. What key data representation techniques are covered in the NCERT Solutions for Class 8 Maths Chapter 4?
The NCERT Solutions for Class 8 Maths Chapter 4 provide detailed methods for several key data representation techniques essential for the syllabus. The main techniques covered are:
- Frequency Distribution Tables: For organising both raw and grouped data.
- Bar Graphs: To compare discrete categories of data.
- Histograms: Specifically for representing grouped data with continuous class intervals.
- Pie Charts (or Circle Graphs): To show the relationship between a whole and its parts.