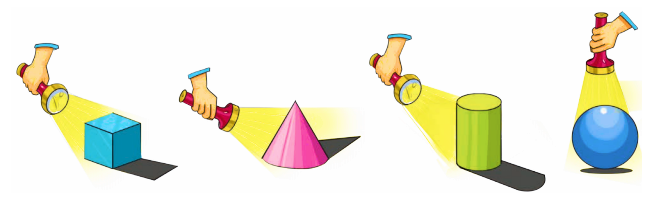
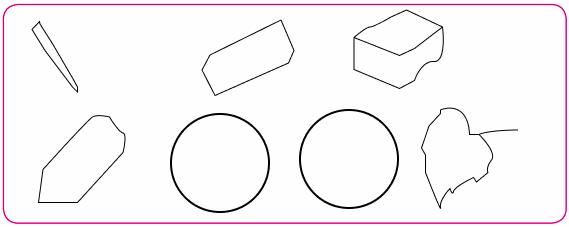
Shadow Story - Exercise-wise Questions and Answers For Class 2 Maths - Free PDF Download
Vedantu provides NCERT Solutions for Class 2 Maths Chapter 4, "Shadow Story (Togalu)," which makes learning about shadows easy and enjoyable for students. This chapter introduces how shadows form, the different shapes they can take, and how they change when the light source moves. NCERT Solutions for Class 2 Maths exercises and examples are designed to help students understand these concepts in a fun and engaging way.
Table of Content
These solutions are included in the CBSE Class 2 Maths syllabus, ensuring that students are covering the necessary topics for their grades. The clear explanations and familiar examples help students easily understand shadows and relate them to what they see in their daily lives. Download the free PDF to help students explore and enjoy learning about shadows simply and enjoyably.
Glance on Class 2 Maths Chapter 4 - Shadow Story (Togalu)
Students will learn how shadows are formed, helping them understand the relationship between light and objects.
The chapter encourages students to observe how shadows change in size and shape depending on the position of the light source.
By learning about shadows, students can connect these concepts to everyday experiences, like noticing shadows outside.
Fun exercises and activities help students stay interested while learning important science concepts.
This chapter introduces students to fundamental ideas about light and shadows, laying the groundwork for more advanced learning in the future.
Let us Talk
A. Have you seen your own shadow or the shadow of a tree, a dog, a cow or any other animal?
Ans: Yes, I have seen my shadow and the shadows of trees, dogs, and other animals.
B. When do we see a shadow?
Ans: We see a shadow when light is blocked by an object, like when standing in sunlight.
C. When does a shadow vanish?
Ans: A shadow vanishes when the light is no longer blocked by the object, or if the light source is removed.
Fun with Shadows
Now put the torch light on the objects around you and observe the shapes of their shadows.
A. Will the size of shadows change on changing the position of the torch?
Ans: Yes, the size of shadows changes by changing the position of the torch.
B. At what time of the day is your shadow longest?
Ans: My shadow is the longest in the morning or late afternoon.
C. At what time of the day is your shadow shortest?
Ans: My shadow is shortest around noon when the sun is directly overhead.
Let us Trace
A. Trace the shape of the objects around you. For example, eraser, leaf, matchbox, sharpener, pencil colour, etc.
Ans:
B. Draw the shapes you get after tracing.
Ans:
Let us Think
Write the names of objects that have the same trace as:
A. Bottle cap ______ ______ ______
Ans:
B. Eraser ______ ______ ______
Ans:
Hide and Seek
Circle ◯ and rectangle ▭ are playing hide and seek. Rectangle is hiding from the circle.
They all are playing together now.
A. Circle ◯ can hide in the clock, ball, ________, ________.
Ans: Circle ◯ can hide in the clock, ball, table, hanging round light.
B. Rectangle ▭ can hide in the shoe box, photo frame, _________, _________.
Ans: Rectangle ▭ can hide in the shoe box, photo frame, door mate, TV.
C. But Triangle △ and Square ◻ are confused and wonder where to hide now. Suggest them some places where they can hide.
i. Triangle △ can hide in _________, _________.
Ans: Triangle △ can hide in cap, wall hanging on door.
ii. Square ◻ can hide in _________, _________.
Ans: Square ◻ can hide in dice, corner table.
Colour the Carpet
Colour the Triangles red. 🔺
Colour the Circles green. 🟩
Colour the Rectangles yellow. 🟨🟨
Colour the Squares blue. 🟦
Ans:
Make your own design with different shapes and colour them.
Ans:
Look at the picture and answer the following questions.
A. Name the children standing near the corners of the table.
Ans: The names of the children who are standing near the corners of the table are Udit, Paramjeet, Naysa and Seema.
B. Can you tell who will clap next?
Ans: Wasim will lap next.
C. Where is Wasim standing?
Ans: Wasim is standing between the corners.
D. Can this game be played around a round table? Why or why not?
Ans: No, this game cannot be played around a round table because it has no corners.
E. Name the objects around us that have straight edges.
Ans: Table, chair, book, wall, almirah.
F. Many objects around us have curved edges. Some are shown below. Explore and share the names of such objects that you see around.
Ans: The names are Lemon, ladoo, tyre, marble, coin.
Let us Think
A. How many corners do objects with curved edges have? _________
Ans: 0
B. Name the objects that have both straight and curved edges? _________, _________ ,_________.
Ans: gas, cylinder, pipe
Origami Fun!
A. Take a paper and fold it to make it a square.
B. It has _________ corners and _________ edges.
Ans: It has 4 corners and 4 edges.
C. Fold it in half by joining two corners as shown in the picture.
D. Tick ✅ the shape which you get.
i. 🟣
ii. 🟪
iii.🔺
Ans: 🔺
E. This shape has ___ corners and ___ edges.
Ans: This shape has 3 corners and 3 edges.
F. Fold the paper again into half to get a triangle and then unfold it.
G. Now make two triangles from two corners of the triangle.
H. How many corners are there now? ___
Ans: 9
I. Fold the third corner upwards and make the nose and eyes as shown.
Patterns
A. Make designs by stamping objects having different shapes like — bottle caps, erasers, pencils, coins, etc.
Ans:
B. Radha is applying mehandi on her hands. You can also trace your hand to make a mehandi pattern or design.
Ans:
Let us Do
Nitya is playing with leaves and making patterns.
Now you also collect some leaves and make a pattern. Paint one side of the leaf and print it on the space given below.
Extend the following patterns.
Ans:
Kikku rabbit jumps on the 4th tile. He forgot where to jump next. Help him by drawing a circle 🟣 on the next tiles.
1, 4, _____, _____, _____, _____, _____, _____
Ans:
Kikku’s mother also jumps on the 6th tile. Help her by putting a ❌ on the next tiles. 1, 6, 11, _____, _____, _____, _____, _____
Ans: 1, 6, 11, 16, 21, 26, 31, 36
Let us Do
Extend the following number patterns.
A. 5, 10, 15, _____ _____ _____ _____ _____
Ans: 5, 10, 15, 20, 25, 30, 35, 40
B. 7, 14, 21, _____ _____ _____ _____ _____
Ans: 7, 14, 21, 28, 35, 42, 49, 56
C. 1, 7, 13, _____ _____ _____ _____ _____
Ans: 1, 7, 13, 19, 25, 31, 37, 43
Benefits of NCERT Solutions for Class 2 Maths Chapter 4 Shadow Story (Togalu)
Chapter 4, "Shadow Story," from Class 2 Maths helps students easily learn to count, compare, and arrange numbers.
The chapter's engaging exercises and colourful illustrations make learning about numbers both enjoyable and fun.
Clear explanations throughout the chapter help students quickly understand concepts like counting, comparing, and ordering numbers.
The practice exercises provided help students improve their counting skills and accurately recognise numbers.
Interactive activities keep students engaged and focused, making the learning process enjoyable.
Important Study Material Links for Class 2 - Shadow Story (Togalu)
Conclusion
The NCERT Solutions for Class 2 Maths Chapter 4, "Shadow Story (Togalu)," make learning about shadows simple and enjoyable. Through clear explanations and engaging activities, students can understand how shadows are created and how they change with light. The chapter helps students connect these ideas to their daily lives and improves their observation skills. With these solutions, students gain a solid grasp of basic science concepts, preparing them for more advanced topics in the future. The fun and interactive nature of the chapter makes learning about shadows both interesting and easy.
Chapter-wise NCERT Solutions Class 2 Maths - Joyful-Mathematics
After going through the Class 2 Maths Chapter 4 Question Answers, students can find detailed NCERT Solutions for all chapters in the Class 2 Joyful-Mathematics textbook.
Related Important Links for Maths Class 2
Along with this, students can also download additional study materials provided by Vedantu for Maths Class 2 –
FAQs on NCERT Solutions For Class 2 Maths Chapter 4 Shadow Story - 2025-26
1. How do Vedantu's NCERT Solutions for Class 2 Maths Chapter 4 make learning about 'Shadow Story' easy?
Vedantu's NCERT Solutions for Class 2 Maths Chapter 4 simplify the concepts in 'Shadow Story' using clear language and relatable examples. The solutions explain the activities from the textbook, demonstrating how shadows are formed and how their shapes and sizes change with the position of the light source, making the topic easy for young students to understand.
2. What types of questions are solved in the NCERT Solutions for Class 2 Maths Chapter 4?
The NCERT Solutions for this chapter provide answers to all the exercises in the textbook. This includes questions that require students to:
- Observe and identify shadows of different objects.
- Draw shadows as they appear at different times of the day.
- Understand how a shadow's length and shape change.
- Match objects to their corresponding shadow outlines.
3. How do the NCERT Solutions explain the connection between a light source and a shadow's size and shape?
The solutions provide a clear, step-by-step explanation for the activities in the chapter. They explain that when an object is closer to the light source, its shadow is larger. Conversely, when the object moves further away from the light, its shadow becomes smaller. This method helps students correctly solve questions about changing shadows.
4. How can I use these NCERT Solutions to check my answers for the 'Shadow Story' chapter exercises?
You can use these NCERT Solutions to verify your answers after attempting the textbook exercises on your own. Compare your method and final answer with the expert-verified solutions provided. This practice helps reinforce learning and ensures you understand the correct concepts as per the 2025-26 CBSE syllabus.
5. How can parents use these NCERT Solutions to help their Class 2 child with homework for this chapter?
Parents can use these solutions to guide their child through the 'Shadow Story' activities. The simple language and clear explanations help parents understand the chapter's objectives, assist their child with practical homework tasks like creating shadow puppets, and explain the underlying concepts without confusion.
6. Why is it important to understand the method used in the NCERT Solutions, not just copy the answers?
Understanding the method is crucial because this chapter focuses on building observational and spatial reasoning skills. Simply copying answers will not help a child learn why shadows behave the way they do. The solutions are designed to teach a thinking process: observe, predict, and then conclude, which is a key skill in both maths and science.
7. How do the solutions for 'Shadow Story' help a child connect the mathematical concept of shapes with the real world?
This chapter, while seemingly about a simple story, is a practical introduction to geometry. The NCERT solutions help students see that real-world objects have specific shapes (like circles, squares, or triangles) and their shadows are 2D representations (projections) of these shapes. By working through the solutions, students learn to identify and correlate 3D objects with their 2D shadows, a foundational geometric concept.
8. What common mistakes do students make in this chapter, and how do the solutions help prevent them?
A common mistake is assuming a shadow is always the same shape and size as the object. The NCERT Solutions prevent this by repeatedly demonstrating how the angle and distance of the light source can distort a shadow, making it longer, shorter, or wider. The step-by-step activities in the solutions provide a correct mental model to avoid this misconception.
9. Beyond just shadows, what foundational skills do students build by using the NCERT Solutions for Chapter 4?
By working through these solutions, students develop critical skills beyond just understanding shadows. They learn cause-and-effect reasoning (moving light causes the shadow to change), enhance their powers of observation, and improve their ability to describe spatial relationships. These skills are fundamental for future learning in more complex maths and science topics.
