Surface Area Complete Guide with Formulas and Examples

Three-dimensional shapes' surface area is one of their most essential characteristics. The surface area of a shape is a topic that comes up frequently in geometry. Using a general formula for surface area, it is possible to solve the objects having simple shapes and forms. We will need to use our understanding of one or more 2-dimensional shapes to handle more challenging shapes.

In this article, we will find the surface area of cube and cuboid as well as cylinder. Moreover, we will determine the formula of total surface area of cuboid, cube and cylinder. We can readily determine their surface area and volume using the established equations. Have you ever considered what may happen if these fundamental shapes combined to create a new shape? How will we determine the new shape's capacity then? This is explained in the article that follows.

Surface Area Definition

Any solid shape's surface area is equal to the sum of all of its faces' respective areas. For instance, we add the areas of each of the rectangles that make up a cuboid to determine its surface area. When calculating the surface area of complex shapes, the combined area of all the surfaces of the shapes that make up a complex structure is calculated.

There are Primarily Two Categories of Areas:

• Total Surface Area

• Curved Surface Area/Lateral Surface Area

Total Surface Area

The total surface area is the area that includes the base(s) and the curving portion. It is the overall area that the object's surface occupies. If the shape has a curved base and surface, the total area will be equal to the sum of the two areas.

Curved Surface Area/Lateral Surface Area

The area of just the curved part of the shape, excluding its base(s), is referred to as the curved surface area. For shapes like a cylinder, it is sometimes referred to as the lateral surface area.

The Below Table shows the Surface Area of the Various Shaped Objects:

Name	Figure	Total Surface Area	Lateral Surface Area
Cube		$6{a^2}$	$4{a^2}$
Cuboid		$2(lb + bh + hl)$	$2h(l + b)$
Cylinder		$2\pi r(r + h)$	$2\pi rh$

Surface Area of Cuboid Formula

1. Total Surface Area of Cuboid : The surface areas of each of the six sides can be added up to determine their total area. Due to the fact that a cuboid's faces are all rectangles, the total surface area of the cuboid is determined by adding the areas of each rectangle on each face. With the guidance of the following figure, let's understand this better.

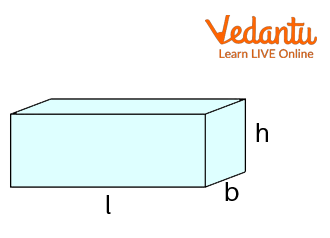
A Cuboid

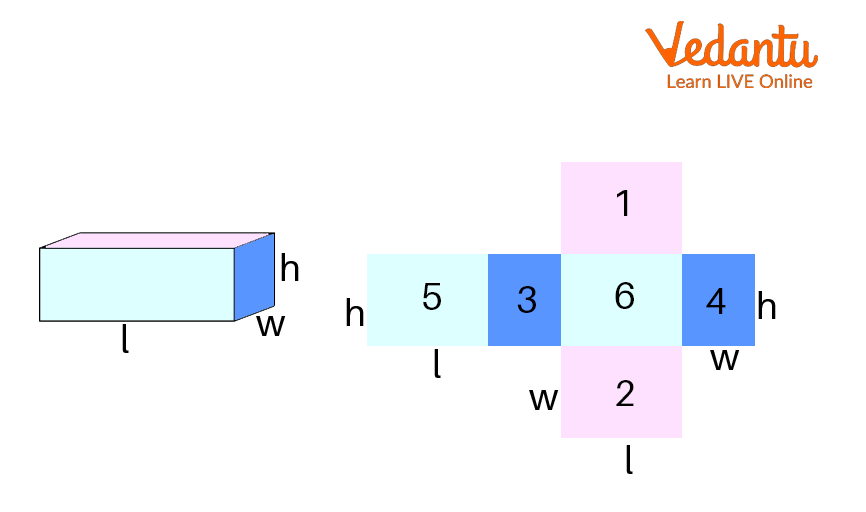
Cuboid with Different Faces

According to the figure above, all of the faces are numbered $1$, $2$, $3$, $4$, $5$ and $6$. In other words, we get this figure if we visualise the cuboid as a two-dimensional net.

• Area of rectangles $1$ and $2$: This refers to the area of the rectangle with the top and bottom faces equal to $l \times w$. As a result, $lw + lw = 2lw$.

• Area of rectangles $3$ and $4$: This refers to the area of the rectangle that comprises the front and back faces and has the dimensions $h \times w$. As a result, it is, $hw + hw = 2hw$ .

• Area of rectangles $5$ and $6$: This refers to the area of the rectangle formed by the faces on the left and right sides, which is equal to $l \times h$. As a result, $lh + lh = 2lh$ .

• The surface area of the six faces is, therefore, equal to $2lw + 2hw + 2lh$. So, a cuboid with $l$, $w$, and $h$ dimensions will have a total surface area of $2(lw + hw + lh)$ .

2. Lateral Surface Area of Cuboid : The total surface area of a cuboid's four vertical sides makes up its lateral surface area of the cuboid. If the top and bottom faces are taken out of the above figure, the lateral surface area of the cuboid will be identified. The cuboid's lateral surface area is

Total Surface Area $ - $ Area of Top and Bottom Faces $ = $ Lateral Surface Area

Lateral Surface Area $ = 2(lw + hw + lh) - 2(lw)$

$ = 2lw + 2hw + 2lh - 2lw$

$ = 2hw + 2lh$

$ = 2h(l + w)$

Surface Area of Cube Formula

1. Total Surface Area of Cube :To determine the area filled by the six surfaces, use the cube's total surface area formula. The cube's total surface area is calculated by multiplying the square of the side length by six. As a result, the formula for the cube's surface area with side length "$a$" is "$6{a^2}$".

A Cube

2. Lateral Surface Area of Cube : The area occupied by the $4$ lateral or side surfaces of the cube is calculated using the cube's lateral surface area formula. The cube's lateral surface area is determined by multiplying its side length’s square by $4$. Therefore, "$4{a^2}$" is the formula for the cube's lateral surface area with side length "$a$".

Surface Area of Cylinder Formula

1. Curved/Lateral Surface Area of Cylinder : A cylinder's curved surface area is the area that is entirely covered by its curved surface. The curved surface area of a cylinder is estimated using the formula below if the height of the cylinder is $h$ and the radius of the base is $r$:

Lateral surface area of cylinder $ = 2\pi rh$

2. Total Surface Area of Cylinder : The area of the two bases as well as the area of the curved surface are added to determine the cylinder's total surface area. Consequently, the following is the formula for the cylinder's total surface area:

Area of the two bases$ + $Area of the curved surface$ = $Cylinder's total surface area.

Due to the cylinder's circular bases, their total area will be equal to $\pi {r^2} + \pi {r^2}$ . We also know that a cylinder's curved surface area is $2\pi rh$.

The cylinder's total surface area is $(\pi {r^2} + \pi {r^2}) + 2\pi rh$ .

Cylinder's total surface area is equal to $2\pi r(r + h)$ .

3. Formulation for the Surface Area of a Cylinder : Any shape's area is the space it occupies. A cylinder has a curving surface that unfolds into a rectangle and two flat surfaces that are both circulars. Look at the cylinder with the provided height ("$h$") and radius ("$r$"). To further understand this, let's open a 2-dimensional cylinder.

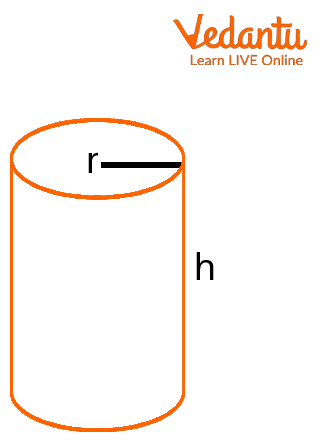
Cylinder

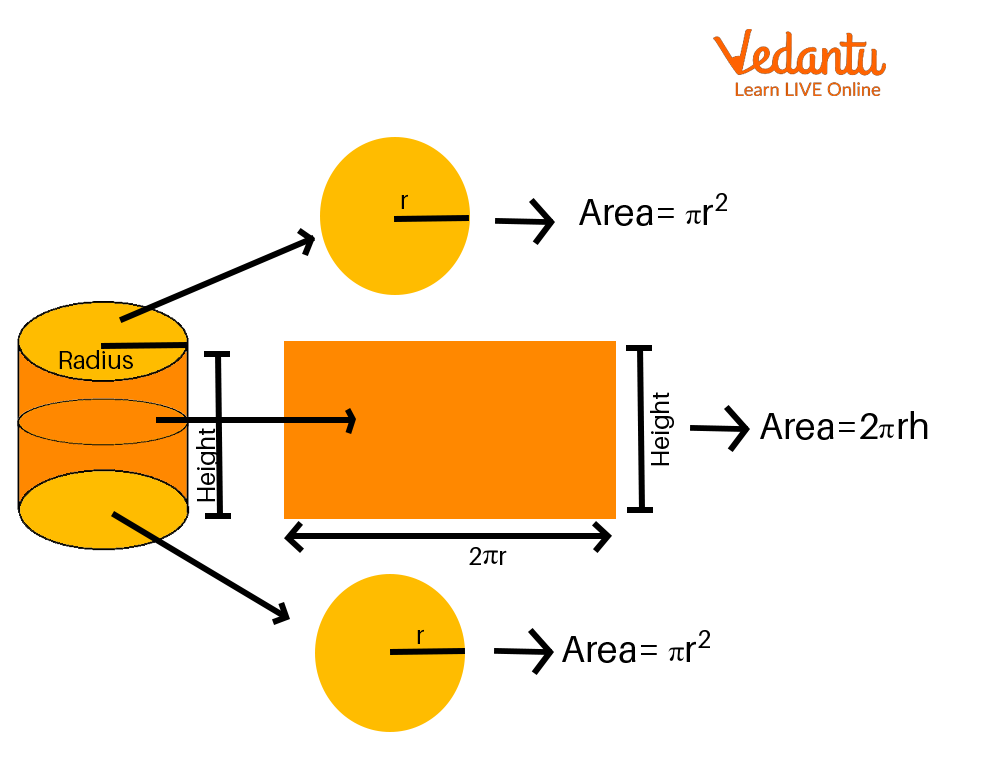
Cylinder Expanded in the Shape of a Rectangle

Look at the figure above, where the two bases are circles and the area of the curved surface expands up as a rectangle.

• The area of the two curves is now $(\pi {r^2} + \pi {r^2})$ , where $r$ is the base radius.

• One side of the rectangle corresponds to the cylinder's height, $h$, and its length, $2\pi r$, to the circle's diameter.

• The area of this rectangle $(l \times b)$ is, therefore, equal to $2\pi r \times h$, which is also the cylinder's curved surface area.

• As a result, the cylinder's total surface area is equal to $2\pi {r^2} + 2\pi rh$ , or $2\pi r(r + h)$ .

Solved Examples

Q.1. Determine the total surface area of a cubic construction whose sidewalls are $7$ metres long.

Solution: Given that the sidewall's length is $7$ metres.

Using the formula, we are aware that

Total Surface Area is $6{a^2}$.

Total Surface Area \[ = 6 \times 7 \times 7 = 294\] sq. m.

Q.2. Determine the surface area of a cylindrical tank with a radius of $4$ yards and a height of $8$ yards using the cylinder's surface area formula. What will the overall cost of the painting be if the cylindrical tank painting costs \[\$ 6\] per square yard?

Solution: We are aware that the formula for a cylinder's total surface area is:

Total Surface Area $ = $ Curved Surface Area + Area of Top and Bottom Faces

\[ = 2\pi rh + 2\pi {r^2} = 2\pi r\left( {r + h} \right) = 2 \times \dfrac{{22}}{7} \times 4\left( {4 + 8} \right) = 301.68\] square yards.

Painting costs come out to \[301.68 \times \$ 6\] per square yard, or \[\$ 1810.08\] .

The cost of the artwork is \[\$ 1810.08\] .

Q.3. Determine the cuboid's total surface area and lateral surface area. Its dimensions are $6$ inches long, $4$ inches wide, and $3$ inches high.

Solution: As is general information, a cuboid's total surface area is equal to \[2\left( {lb + bh + lh} \right)\]and its lateral surface area is equal to $2h(l + b)$.

Here, the dimensions are $6$ inches long, $4$ inches wide, and $3$ inches tall.

Total surface area of the cuboid is equal to \[2\left( {lb + bh + lh} \right) = 2{\text{ }}\left[ {\left( {6 \times 4} \right) + \left( {4 \times 3} \right) + \left( {6 \times 3} \right)} \right]\] sq. inches

Cuboid's total surface area $ = 108$ sq. inches.

Cuboid's lateral surface area is equal to \[2h\left( {l + w} \right) = 2 \times 3\left( {6 + 4} \right)\] sq. inches and is therefore equal to \[60\] sq. inches.

As a result, the cuboid's lateral surface area is \[60\] sq. inches and its total surface area is $108$ sq. inches.

Practice Questions

1. Obtain the surface area of the cube where the edge is $4$ inches using the cube's surface area formula.

2. Identify the total surface area of a cylindrical container with a \[28\] cm diameter and a $15$ cm height.

Answers

1. $96$ sq. inches

2. \[2552\] sq. cm

Summary

The surface area of an object is the total area occupied by all of its surfaces. Two categories—Curved Surface Area (CSA) and Lateral Surface Area (LSA), respectively—are used to categorise the surface's area (TSA). The term "curved surface area," also referred to as "lateral surface area," refers to the surface area of a surface which is curved in shape. The bottom and top sections, as well as the lateral surface area, make up the overall surface area. The three-dimensional shapes' surface areas are included in this article. It greatly facilitates the speedy resolution of issues based on it.