




Visual Method Explained: Plotting and Interpreting Solutions
The mathematical expressions of variables and constants along with the mathematical operations form an equation of the highest degree one. When plotted on a graph, a linear equation is an algebraic equation between variables that produces a straight line. A linear equation of one variable is of the form ax + b = 0 where x is the variable. Linear equations of two variables are of the form ax + by + c = 0 where x and y are the two variables and c is the constant. A pair of linear equations can be solved and represented using two basic methods: the graphical method and the algebraic method. In this article, we are going to learn about solving linear equations graphically.

Examples of Linear Equations
System of Linear Equations
A group of more than one linear equation is commonly known as a system of linear equations. For solutions, we can solve the system of linear equations graphically.
Solving Linear Equations in Two Variables
The solution to linear equations comes in a pair (x, y), one value for the variable x and one value for the variable y. Thus, the solutions for any linear equation in two variables in the form ax+by-c = 0 represent a particular point on the cartesian plane. The graph of a linear equation is always a straight line, no matter what the solutions are.
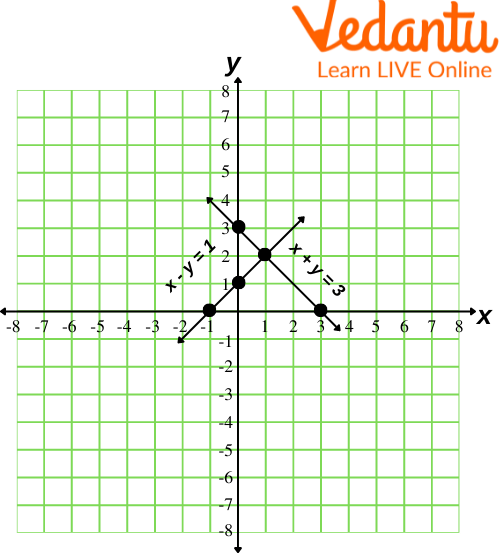
System of Linear Equations
How to Plot the Equations on a Graph
If there is one point of intersection, there is one solution. The x and y coordinates of the point of intersection are the values for the variables that are common between the two equations.
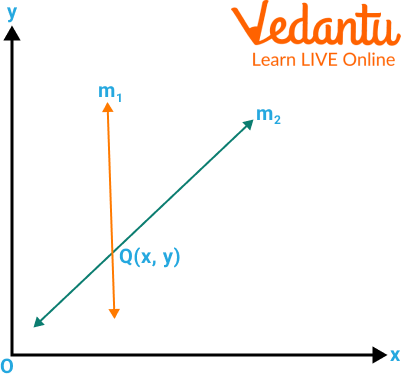
One Solution
If the lines coincide, then there are infinitely many solutions.
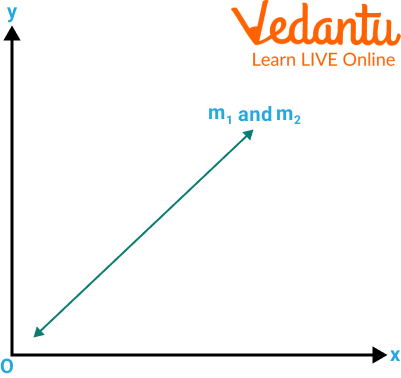
Many Solution
If the lines are parallel, there is no solution.
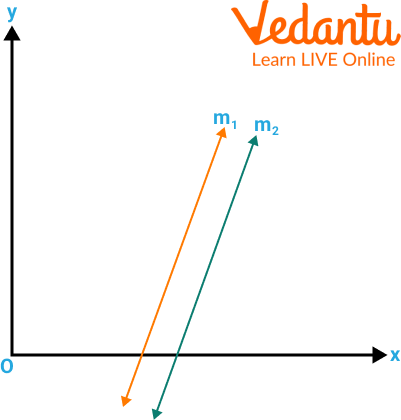
No Solution
Solved Example
1. Check whether the equation $y = 5x + 4$ is linear or not.
Ans: An equation is considered linear if it is in the form of $y=m x+b$ where $\mathrm{m}$ is the slope of the equation and $\mathrm{b}$ is the $\mathrm{y}$-intercept.
Here, $x$ can only be to the power of one.
Since $y = 5x + 4$ is in the form of $y=m x+b$ and x is having power 1. Therefore, the equation is linear.
2. Check whether the equation $y=3 x^2+1$ is linear or not.
Ans: Here, the power of x is more than 1. And for linearity, the power should be 1. Hence, the given equation is not linear.
3. What are the variable and contents in the given equation: $\dfrac{1}{\sqrt{2+x}}=1$
Ans:
Variables: x
Constants: 2
Practice Questions
1. Check whether the equation $y = 9x + 10$ is linear or not.
Ans: Linear
2. Check whether the equation $y=2 x^5+10$ is linear or not.
Ans: Not Linear
3. Check whether the equation $y=4 x^2+ z$ is linear or not.
Ans: Not Linear
Summary
A linear equation is in the form of ax+by+c=0, where a and b are not equal to zero. A linear equation in two variables is an equation that contains two variables (x, y) and the highest degree of the equation is 1. A group of more than one linear equation is known as a system of linear equations. The solution to a system of linear equations in two variables can be found by solving the system graphically. To solve it graphically, the equations have to be graphed individually and then their point(s) of intersection determines the common solution.
FAQs on Solve System of Linear Equations Graphically
1. What is a system of linear equations in two variables?
A system of linear equations consists of two or more linear equations that share the same variables. For example, in two variables (x and y), it would be a pair of equations like ax + by = c and dx + ey = f. The goal is to find a single coordinate pair (x, y) that satisfies both equations simultaneously. This point represents the solution to the system.
2. How do you solve a system of linear equations graphically?
To solve a system of linear equations graphically, you treat each equation as a separate line on a Cartesian plane. The steps are:
For each equation, find at least two coordinate pairs (x, y) that satisfy it. A simple way is to find the x and y-intercepts.
Plot these points on a graph and draw a straight line through them for each equation.
Observe the relationship between the two lines. The point where the lines intersect is the solution (x, y) to the system.
3. What are the three possible outcomes when graphing a system of linear equations?
When you graph a system of two linear equations, there are three possible graphical outcomes, each corresponding to a different type of solution:
Intersecting Lines: The lines cross at a single point. This indicates there is one unique solution.
Parallel Lines: The lines never cross. This means there is no solution to the system.
Coincident Lines: The lines are identical and overlap completely. This indicates there are infinitely many solutions, as every point on the line satisfies both equations.
4. Why are these equations called 'linear'?
An equation is called 'linear' because its graph is a straight line. This happens because the highest power of any variable in the equation is one. There are no variables with exponents (like x²), no variables in the denominator, and no variables multiplied together. This simple, first-degree relationship between variables always produces a straight line when plotted on a graph.
5. What is the difference between a 'consistent' and an 'inconsistent' system of linear equations?
The terms 'consistent' and 'inconsistent' describe whether a system has a solution.
A consistent system is one that has at least one solution. This includes systems with a single unique solution (intersecting lines) and those with infinitely many solutions (coincident lines).
An inconsistent system is one that has no solution at all. Graphically, this is represented by two parallel lines that never meet.
6. How can you determine the type of solution without actually graphing the equations?
You can predict the type of solution by comparing the ratios of the coefficients of the variables in the standard form (a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0):
For a unique solution (intersecting lines), the ratio of x-coefficients is not equal to the ratio of y-coefficients: a₁/a₂ ≠ b₁/b₂.
For no solution (parallel lines), the ratios of x and y-coefficients are equal, but not equal to the ratio of the constant terms: a₁/a₂ = b₁/b₂ ≠ c₁/c₂.
For infinitely many solutions (coincident lines), all three ratios are equal: a₁/a₂ = b₁/b₂ = c₁/c₂.
7. What is a real-world example of using a system of linear equations?
A common real-world application is in making financial decisions, such as choosing between two pricing plans. Imagine two gym memberships:
Gym A: ₹500 joining fee plus ₹100 per month.
Gym B: No joining fee but ₹150 per month.
By setting up a system of linear equations (Cost = 500 + 100x and Cost = 150x), you can graph them to find the 'break-even' point. The point of intersection shows the exact number of months at which both gym memberships would cost the same amount.























