Sandwich Theorem in Calculus Explained Clearly

We may have encountered several theorems in calculus, most notably when calculating the challenging limits and derivatives of functions. Although there are several theorems and formulas for determining the limits of different kinds of functions, we always look for the simplest technique to solve them to obtain the answer quickly. One such use to resolve limit problems is the sandwich theorem.

In calculus, especially mathematical analysis, the Sandwich theorem is typically applied. This theorem is likely used to determine a function's limit by comparing it to two other functions whose limits are known or can be calculated with certainty. This article explains the sandwich theorem and how to apply it to various calculus problems.

History of Carl Friedrich Gauss

To compute π, the mathematicians Archimedes and Eudoxus utilised it for the first time geometrically. Carl Friedrich Gauss then expressed it in more contemporary terms.

Carl Friedrich Gauss (30 April 1777 – 23 February 1855)

What is the Sandwich Theorem in Limits?

Let f, g, and h be real functions such that for any x in the shared definition domain, f(x), g(x), and h(x) occurs. If "a" is a real number, then

$\begin{array}{l}\mathop {{\rm{\;}}\lim }\limits_{x \to a} f\left( x \right)\;\; = \;\mathop {lim}\limits_{x \to a} h\left( x \right)\; = \;t\\{\rm{then}}\;\mathop {\lim }\limits_{x \to a} g\left( x \right)\; = \;t\end{array}$

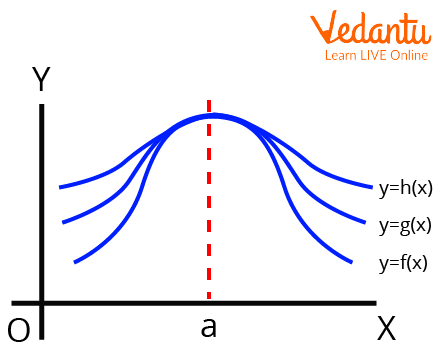
Sandwich Theorem

Sandwich Theorem Proof

Let's examine the geometric proof for the aforementioned claim using a trigonometric inequality.

$Cosx < \dfrac{Sinx}{x} < 1$

Proof of The Sandwich Theorem

We can see the triangles, ΔABE, ΔADF, ΔADB, and sector ADB in the above diagram.

\[; Area \; of (\triangle ABD)< \; Area \; of \; sector \; ADB< \; Area \; of (\triangle ADF)\\ \Rightarrow  \dfrac{1}{2}AD\cdot EB < \dfrac{x}{ 2\pi}\pi \cdot  AD^{2}< \dfrac{1}{2}AD\cdot DF\]

By eliminating the common terms from all sides,

${\rm{EB}} < x.AD < {\rm{ DF}}$

Since angle A = angle X,

EB = AB Sin(x) (from $\triangle ABE$),

and ${\mathop{\rm Sin}\nolimits} A = \dfrac{{EB}}{{AB}}$.

$DF = AD\tan x$ because $\tan x = \dfrac{{DF}}{{AD}}$.

However, $tan {A} = \dfrac{Sin{x}}{Cos{x}}$.

Consequently,

$AD\cdot Sin{x} < x\cdot AD<AD\cdot \dfrac{Sin{x}}{Cos{x}} \\ \Rightarrow 1< \dfrac{x}{Sin{x}}<\dfrac{1}{Cos{x}}$

By taking reciprocals,

$\cos x\; <\dfrac{Sin{x}}{x} < 1$

Hence Proved.

We can simply demonstrate some other trigonometric identities using the aforementioned theory, including

$\displaystyle \lim_{ x \to 0}\dfrac {Sin{x}}{x} = 1 \\ \displaystyle \lim_{ x \to 0}\dfrac {1- Cos{x}}{x} = 0$

Applications of Sandwich Theorem

• To determine the limits of specific trigonometric functions, utilise the Sandwich rule.

• It can be applied to link certain sequences between other known sequences that also converge to the same place to demonstrate the convergence of those sequences.

Sandwich Theorem Examples

1. Evaluate $\displaystyle \lim_{ x\to 0 } \dfrac {tan{x}}{x}$.

Ans: Using the trigonometric identity,

$\begin{array}{l}\tan x\; = \dfrac{{\;\sin x}}{{\cos x}}\\\therefore \mathop {\lim }\limits_{x \to 0} \;\dfrac{{\sin x}}{{x\cos x}}\; = \;\mathop {\lim }\limits_{x \to 0} \;\dfrac{{\sin x}}{x}\cdot\mathop {\lim }\limits_{x \to 0} \;\dfrac{1}{{\cos x}}\end{array}$

And from the Sandwich theorem, we know

$\displaystyle \lim_{ x\to 0 } \dfrac {Sin{x}}{x} = 1$

$ \displaystyle \lim_{ x\to 0 } \dfrac {1}{Cos{x}} = 1 $

Therefore,

$1\cdot1\; = \;1$

2. Prove that $\mathop {\lim }\limits_{x \to 0} \sin x\; = \;0$.

Ans: As known,

$-x \leq Sinx \leq x$ for all $x \geq 0$

$\displaystyle \lim_{x \to 0}(-x) = 0 $ and $ \displaystyle \lim_{x \to 0}(x) = 0$

By Sandwich Theorem,

$\mathop {\lim }\limits_{x \to 0} \left( {Sinx} \right)\; = \;0$

3. Evaluate $\mathop {\lim }\limits_{x \to 0} x\left[ {\left[ {\dfrac{1}{x}} \right] + \left[ {\dfrac{2}{x}} \right] + ...... + \left[ {\dfrac{{15}}{x}} \right]} \right]$.

Ans: Expand the given term as follows:

$\dfrac{1}{x} - 1\leq \left [ \dfrac{1}{x} \right ]\leq \dfrac{1}{x}+1\\ \dfrac{2}{x} - 1\leq \left [ \dfrac{2}{x} \right ]\leq \dfrac{2}{x}+1 \\ \dfrac{15}{x} - 1\leq \left [ \dfrac{15}{x} \right ]\leq \dfrac{15}{x}+1$

Adding them all up, we get

$\dfrac{120}{x} -15 \leq \left [ \dfrac{1}{x} \right ]+\left [ \dfrac{2}{x} \right ]+\cdots +\left [ \dfrac{15}{x} \right ]\leq \dfrac{120}{x} +15\\ \Rightarrow 120 -15x \leq x\left [ \left [ \dfrac{1}{x} \right ]+\left [ \dfrac{2}{x} \right ]+\cdots +\left [ \dfrac{15}{x} \right ] \right]\leq 120+15x \\ \Rightarrow \displaystyle \lim_{x \to 0}(120 -15x) \leq x\left [ \left [ \dfrac{1}{x} \right ]+\left [ \dfrac{2}{x} \right ]+\cdots +\left [ \dfrac{15}{x} \right ] \right]\leq \displaystyle \lim_{x \to 0}(120+15x)\\ 120 \leq x\left [ \left [ \dfrac{1}{x} \right ]+\left [ \dfrac{2}{x} \right ]+\cdots +\left [ \dfrac{15}{x} \right ] \right]\leq 120$

This gives

$\displaystyle \lim_{x \to 0}x\left [ \left [ \dfrac{1}{x} \right ] +\left [ \dfrac{2}{x} \right ]+ \cdots +\left [ \dfrac{15}{x} \right ]\right ] = 120$

Important Points to Remember

• This theorem is probably utilised to establish the limit of the function in question.

• All the functions considered must be real.

Important Formula to Remember

According to the Sandwich theorem,

If $\begin{array}{l}\mathop {{\rm{\;}}\lim }\limits_{x \to a} f\left( x \right)\;\; = \;\mathop {lim}\limits_{x \to a} h\left( x \right)\; = \;t\\{\rm{then}}\;\mathop {\lim }\limits_{x \to a} g\left( x \right)\; = \;t\end{array}$

Conclusion

In this article, we have thoroughly discussed the Sandwich theorem and its proof. From the discussion above about the Sandwich theorem, we can conclude that the Sandwich theorem allows us to determine the limit of a single function by using the limits of the two other functions that is "sandwiched" between these two. When a function gets complex or intricate, or perhaps when we are unable to identify the limit using other techniques, we apply the Sandwich theorem to determine its limit.