




How to Solve Right Circular Cylinder Problems Step by Step
Right circular cylinder is a three-dimensional solid figure. On both ends of the right circular cylinder, which are parallel to one another, there is a closed circular surface. The right cylinder is another name for a right circular cylinder. All of the points on the closed surface are equally spaced from the axis of the right circular cylinder. A cylinder has two curved edges, one curved surface and two flat circular faces. In everyday life, a right circular cylinder is the most typical 3D figure.
What is a Right Circular Cylinder?
Right circular cylinders are three-dimensional solid shapes made up of two parallel bases connected by a closed circular surface, with each base resembling a disk-shaped circle. The axis of the right cylinder is the line that connects the centres of two circular bases or runs through their middles.
Height, or "h," stands for the perpendicular distance, which is the distance between the cylinder's two bases. The radius of the right circular cylinder, denoted by "r," is the measurement from the centre to the outside border for either of the two bases. As a result, two circles and a rectangle combine to create a right circular cylinder.
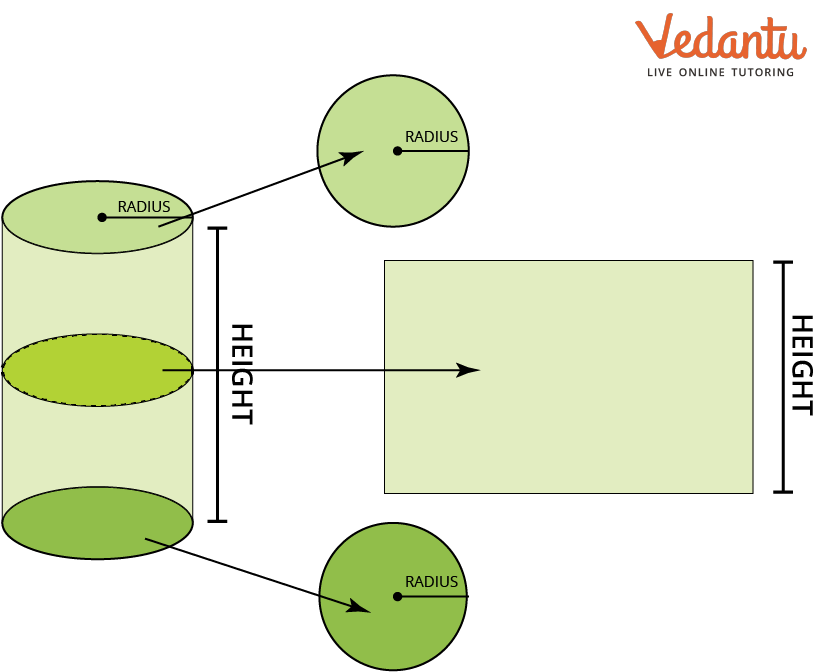
Right Circular Cylinder
Properties of Right Circular Cylinder
Like any two-dimensional shape, the right circular cylinder possesses the following characteristics:
It has one curved surface and two flat surfaces.
Cylindrical bases are always parallel to one another.
The cylinder's area and volume are determined by its height as well as the radius of its base.
The bases are perfectly above one another, and the axis makes a right angle with them.
It lacks a vertex or a corner.
The cylinder's top and bottom are always exact replicas of one another.
The axis is the line that connects the circle's centres.
A right cylinder is created when a rectangle is rotated around one side as the axis of rotation.
The rectangle is the portion that results from cutting a right circular cylinder with a plane that has two components and runs parallel to the cylinder's axis.
A circle is formed when a plane cuts the right cylinder horizontally and parallel to the bases.
Surface Area of Right Circular Cylinder
The area that the right circular cylinder's surface covers is referred to as the surface area of the right circular cylinder. A right circular cylinder's surface regions may be divided into two types:
1. Curved Surface Area of Right Circular Cylinder
It is also known as the right circular cylinder's lateral surface area. It is the space between the parallel circular bases of the right circular cylinder, which is covered by the curved surface of the cylinder.
The formula for curved surface area is
Curved Surface Area (CSA) = $2\pi rh$ square units.
Where “r” is the radius and “h” is the height of the cylinder.
2. Total Surface Area of Right Circular Cylinder
It is described as the region that the complete cylinder fills. There are two circles and a curved surface in this region of the cylinder. So, in order to calculate the right circular cylinder's total surface area, we sum the areas of the two circles and the curved surface at the end.
The total surface area is given as:
Total Surface Area (TSA) = $2\pi r h + 2\pi {r^2} = 2\pi r(h + r)$ square units.
Where “r” is the radius and “h” is the height of the cylinder.
Volume of Right Circular Cylinder
The quantity of space occupied by a right circular cylinder is referred to as its volume. In terms of cubic units, the volume of the right circular cylinder is expressed as (m3, cm3, in3, or ft3).
The formula for volume of right circular cylinder is:
Volume of cylinder = Area of Circle x Height
Volume = $\pi {r^2} h$ cubic units
Where “r” is the radius and “h” is the height of the cylinder.
Cylinder Examples in Real Life
From soda cans to toilet paper to water pipelines, cylinders are everywhere in our life. Some examples of cylinders are:
Water tanks
Candles
Battery
Test tube
Beakers

Juice Cans
Problems on Right Circular Cylinders
Let us look at some question on cylinder which will also include volume of a cylinder problems and cylinder word problem:
Example 1: The volume of a right circular cylinder is 7040 in3. If its radius is 4 in, find its height. (use $\pi = \dfrac{{22}}{7}{\rm{ ~or~ }}3.14$)
Solution: Volume of cylinder = $440~i{n^3}$
To find the height, the formula to be used is
$\begin{array}{l}V = \pi {r^2} \times h\\7040 = \dfrac{{22}}{7} \times {4^2} \times h\\h = \dfrac{{7040 \times 7}}{{22 \times 16}}\\h = 140~in\end{array}$
Hence, the height of the cylinder is 140 in.
Example 2: Find the volume of a right cylinder, if the radius and height of the cylinder are 20 cm and 30 cm respectively. (use $\pi = \dfrac{{22}}{7}{\rm{ ~or~ }}3.14$)
Solution:
Given: r = 20 cm, h = 30 cm
Volume of the cylinder is given as:
$\begin{array}{l}V = \pi {r^2}h\\V = 3.14 \times {20^2} \times 30\\V = 37680~c{m^3}\end{array}$
Hence, the volume of the cylinder is 37680 cm3.
Conclusion
We now have a basic understanding of the right circular cylinder and its key components due to this article. This article covered topics like surface area and volume of the right circular cylinder. Properties of the right circular cylinder is also discussed and now we have a good knowledge about the circular cylinder. The problems related to cylinders can be solved using the formulas discussed in this article. Some real life examples of circular cylinders are also mentioned.
FAQs on Right Circular Cylinder Problems: Key Concepts & Solved Examples
1. What is a right circular cylinder and how is it different from an oblique cylinder?
A right circular cylinder is a three-dimensional shape with two parallel, circular bases positioned directly above each other. Its defining feature is that its axis (the line connecting the centers of the bases) is perpendicular, or at a 90-degree angle, to its bases. In contrast, an oblique cylinder also has two parallel circular bases, but its axis is not perpendicular to them, giving it a slanted or tilted appearance.
2. What are the key formulas to calculate the surface area of a right circular cylinder?
The surface area of a right circular cylinder is calculated using two primary formulas based on the area required:
- Curved Surface Area (CSA): This measures only the area of the curved vertical surface. The formula is CSA = 2πrh.
- Total Surface Area (TSA): This is the total area of the entire object, including the curved surface and the two circular bases. The formula is TSA = 2πrh + 2πr², which is often simplified to 2πr(h + r).
In these formulas, 'r' represents the radius of the base and 'h' is the height of the cylinder.
3. How do you calculate the volume of a right circular cylinder?
To find the volume of a right circular cylinder, you need to multiply the area of its circular base by its height. The formula is Volume (V) = πr²h. Here, 'π' (pi) is a constant approximately equal to 3.14, 'r' is the radius of the circular base, and 'h' is the perpendicular height of the cylinder. The result is always expressed in cubic units, such as cm³ or m³.
4. What are some examples of right circular cylinders in everyday life?
Right circular cylinders are one of the most common shapes found in our daily surroundings. Some practical examples include:
- Food and beverage cans, like those for soda or soup.
- Common household items such as candles, batteries, and toilet paper rolls.
- Larger infrastructure like water storage tanks, pipes, and cylindrical support pillars.
5. Why must the bases of a right circular cylinder be parallel and congruent?
The properties of being parallel and congruent are fundamental to the definition of a right circular cylinder, which is generated by rotating a rectangle around one of its sides. The two sides of the rectangle that are parallel to the axis of rotation trace out the top and bottom circular bases. Because these sides are equal in length and remain at a constant distance from each other throughout the rotation, they naturally form two identical (congruent) and parallel circles.
6. How does the volume of a cylinder change if its radius is doubled but its height is halved?
If the radius is doubled and the height is halved, the volume of the cylinder doubles. This can be demonstrated using the volume formula V = πr²h. Let the new radius be 2r and the new height be h/2. The new volume (V') would be:
V' = π(2r)²(h/2)
V' = π(4r²)(h/2)
V' = 2(πr²h) = 2V.
This shows that the volume of a cylinder is more significantly impacted by changes in its radius than its height, as the radius is a squared term in the formula.
7. What is the difference between the Curved Surface Area (CSA) and Total Surface Area (TSA) of a cylinder?
The primary difference between CSA and TSA is which parts of the cylinder are being measured:
- The Curved Surface Area (CSA) refers only to the area of the curved vertical face that connects the two circular bases. A simple analogy is the paper label on a tin can.
- The Total Surface Area (TSA) accounts for the entire surface of the cylinder. It is the sum of the CSA and the area of the two flat circular bases (the top and the bottom).
8. What 2D shape is formed if you cut a right circular cylinder parallel to its axis?
If you make a straight cut through a right circular cylinder with a plane that is parallel to its axis, the resulting cross-section is a rectangle. The length of this rectangle will be equal to the height of the cylinder, and its width will be determined by how close the cut is to the center of the cylinder's base. If the cut passes directly through the center, the width of the rectangle will be equal to the diameter of the cylinder's base.

















