




How to Find and Apply the Prime Factors of 210
In mathematics, a factor is a divisor of a given integer that divides it exactly, leaving no leftover. We can use various techniques, including the division and multiplication methods, to identify a number's factors. The fact that 210 can be divided by one, at least by 2, 3, and 5, makes it a composite number. An integer is considered composite if it can be divided by at least one other natural number, in addition to itself and 1, without producing a residual (divided exactly).
Factors of 210
Any integer that can be multiplied by another integer to produce the exact number 210 is a factor of that number. Finding the factors of 210 is equivalent to breaking the number 210 into all the smaller components that can be multiplied to make the number 210.
When we describe the factors of 210, what we mean refers to all the positive and negative whole numbers that can be divided by 210 in an even number of portions. The result would be another factor of 210 if you took 210 and divided it by one of its factors.
The following are the positive and negative factors of 210:
Positive factors of 210: 1, 2, 3, 5, 6, 7, 10, 14, 15, 21, 30, 35, 42, 70, 105, 210
Negative factors of 210: -1, -2, -3, -5, -6, -7, -10, -14, -15, -21, -30, -35, -42, -70, -105, -210.
How to Find Factors of 210?
In the above section, we defined a factor as a number that divides evenly into 210. Therefore, the method for identifying and making a list of all the factors of 210 is to check every number up to and including 210 and verify which numbers have an even quotient (which means no decimal place).
The factors of 210 are mentioned below:
$210 \div 1 = 210$
\[210 \div 2 = 105\]
\[210 \div 3 = 70\]
\[210 \div 5 = 42\]
\[210 \div 6 = 35\]
\[210 \div 7 = 30\]
\[210 \div 10 = 21\]
\[210 \div 14 = 15\]
\[210 \div 15 = 14\]
\[210 \div 21 = 10\]
\[210 \div 30 = 7\]
\[210 \div 35 = 6\]
\[210 \div 42 = 5\]
\[210 \div 70 = 3\]
\[210 \div 105 = 2\]
$210 \div 210 = 1$
So, here is a list of all 210 factors: 1, 2, 3, 5, 6, 7, 10, 14, 15, 21, 30, 35, 42, 70, 105, 210.
Prime Factorization of 210
A composite number is expressed as the product of its prime factors when it is the prime factor. We shall divide 210 by its smallest prime factor, 2, to obtain its prime factorization.
$210 \div 2 = 105$
Now, multiply 105 by its smallest prime factor to get the quotient. This process continues until the quotient equals 1. The figure below displays 210's prime factorization.

Prime Factorisation of 210
Factor Tree of 210
A number being divisible for a certain divisor is referred to as being divisible. In a diagram known as a number's factor tree, starting from a given number, you identify its factors, then the factors of those smaller numbers, and so on, until you run out of numbers to factor.
210 is $10 \times 21$, hence the factor tree for this number will look like this:

Factor tree
Factor Pairs of 210
Let's find out what two integers when multiplied together, result in the number 210. Each factor can be combined with another factor to create 210.
The steps below help you to generate the factor pairs for 210:
Step 1: Choose the smallest prime number that is a factor of 210, larger than 1. 2, 3, 5, 7, 11, and 13 will be the first prime numbers to verify as a reference. The smallest component in this example that is a prime number greater than one is two.
Step 2: 210 divided by the smallest prime number, in this case, 2, generate
$210 \div 2 = 105$
Thus, a new factor pair is formed by 2 and 105.
Step 3: Use 105 from Steps 1 and 2. Divide 105 by the lowest prime factor now, this time it is 3, the new smallest prime factor.
$105 \div 3 = 35$
Step 4: You should keep in mind that this new factor pair only applies to factors of 105, not 210. Therefore, you would multiply 2 and 3 before pairing with 35 to finalise the factor pair for 210:
$2 \times 3 = 6$
Step 5: Continue doing this when there are no more prime factors larger than one left to divide by. The complete list of factor pairs will be generated after all these steps.
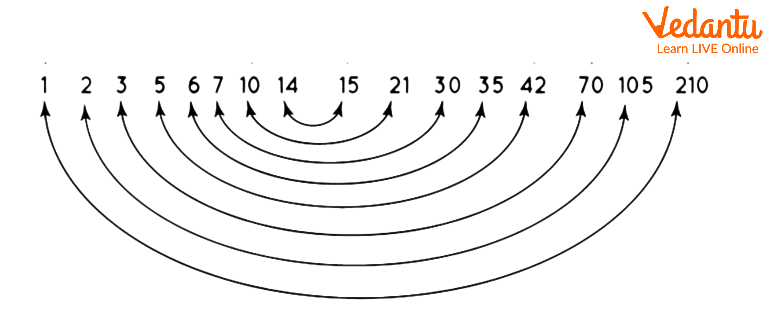
Pair factors of 210
The factor pairs for 210 are listed below:
(1, 210), (2, 105), (3, 70), (5, 42), (6, 35), (7, 30), (10, 21), (14, 15)
The negative pair factors of 210 are (-1, -210), (-2, -105), (-3, -70), (- 5, -42), (-6, -35), (-7, -30), (-10, -21), and (-14, -15).
Solved Examples
Example 1: Determine the product of 210 prime factors.
Solution: The Product of Prime Factors of 210 is:
$2 \times 3 \times 5 \times 7 = 210$.
Example 2: Is 70 a factor of 210?
Solution: Yes, a factor of 210 is 70. If 70 can be used to divide 210, the result is a quotient of 3 and a remainder of 0, proving that 70 is a factor of 210.
Practise Problems
1. Determine the sum of all positive factors of 210.
2. Find the GCF of 70 and 210.
Answers
1. 576.
2. 70.
Related Topics
Summary
Let’s summarise what we have learned in this article: 1, 2, 3, 5, 6, 7, 10, 14, 15, 21, 30, 35, 42, 70, 105 and 210 are all factors of 210. Factors of 210 are 16 integers in total. 105 is the largest factor of 210. 2, 3, 5, and 7 are the number 210's prime factors. The result of multiplying these numbers together is 210. So, here is a list of all 210 factors: 1, 2, 3, 5, 6, 7, 10, 14, 15, 21, 30, 35, 42, 70, 105, 210. The 210 negative factors are: -1, -2, -3, -5, -6, -7, -10, -14, -15, -21, -30, -35, -42, -70, -105, -210.
FAQs on Prime Factorization of 210
1: How will you determine the greatest common factor of 210 and another number?
By comparing the prime factorization of the two numbers and taking the highest common prime factor, it is possible to find the biggest common factor between them. The HCF is 1 if there is no common factor. This is one of the common prime factors of two numbers and is also known as the highest common factor. It is the biggest prime factor that the two numbers have in common.
2: Why is 210 known as the triangular number?
Natural numbers expressed as a sum are known as triangular numbers. If we can arrange all 210 with perfect symmetry to form an equilateral triangle, then the number 210 is a triangular number. The following equation must be true to establish whether or not a number (n) is a triangular number:
$\sqrt{(8 × n) +1} = Integer$
Therefore, $\sqrt{(8 × 210) +1} = 41$ and 41 is an integer.
3: Is 210 a composite or prime number?
210 is not a prime number. Depending on the number of factors it contains, a number may have only two factors, or more than two numbers can be categorised as prime or composite. Composite numbers have more than 2 factors. Because 210 has multiple factors, namely 1, 2, 3, 5, 6, 7, 10, 14, 15, 21, 30, 35, 42, 70, 105, 210. In other words, the fact that 210 has more than two factors makes it a composite number.

















