Normal Form of a Line Formula Derivation and Solved Examples
Lines are the basic geometry in mathematics. We have many types of lines as we will learn later in this chapter. As we see every polygon is a set of line segments. And a line is a set of points. Here we will learn how points decide a line. And how we use it in our daily graph calculations.
What Is Line:
A line is a 1D figure. Which has length but not width. To understand a line we can say that a line is a collection of so many points. And every point is in the opposite direction. Every line has at least two fixed points as a minimum. The line is infinite in both directions. It doesn't have any limits.
Line
Then there is another form of a line which is called a Line segment. It is called a line segment. It is just a part of the line. It has its limits in both directions.
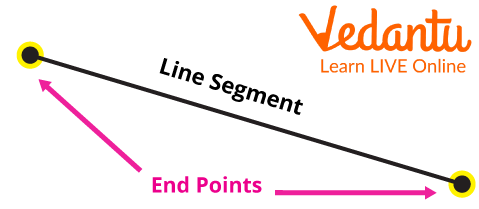
Line Segment
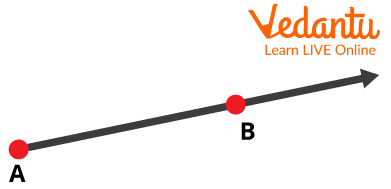
The last form of a line is Ray. It is a line that passes through two fixed points in which one point of this line is fixed and the other one is limitless.
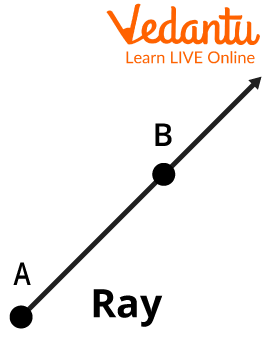
Ray
Now, Look at the difference between these all.
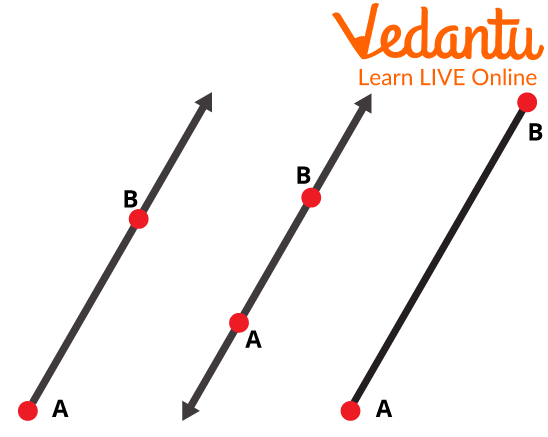
Ray, Line, Segment
The 1st one is a “Ray”.
2nd is a “Line”.
The 3rd one is the “Line segment”.
General Equation Of a Straight Line:
It is also known as “The general equation” of a line. We mostly derive it from the help of coordinate geometry.
The equation is:
\[y = mx + c\]
“m” is the gradient.
For example:
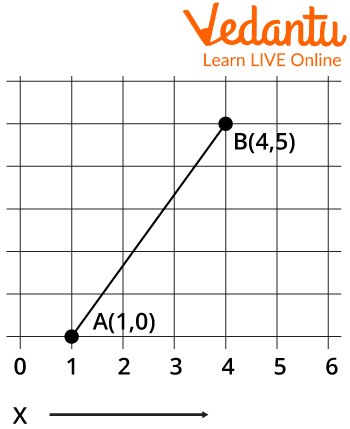
Line which has Coordinate A(1,0) and B(4, 5)
We can write its equation as :
Finding slope(m) = \[\frac{{5 - 0}}{{4 - 1}} = \frac{5}{3}\]
Substituting m into the equation:- y = mx + c
\[\Rightarrow y = \frac{5}{3}x + c\]
Now put any 1 coordinate value in this equation and find the value of C,
\[ \Rightarrow 0 = \frac{5}{3} \times 1 + c\]
\[ \Rightarrow - c = \frac{5}{3}\]
The equation we get is –
\[y = \frac{5}{3}x - \frac{5}{3} \Rightarrow 3y = 5x - 5;\]
The Equation Of Straight Line In Normal Form:
Now let’s get to the normal form of line which is mostly used in geometry.
Here we have an example diagram of normal form derivation.
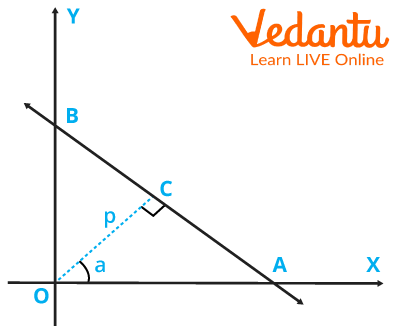
A Line Crossing through point A on the X-axis and B on the Y-axis, P is the Perpendicular on AB from the Origin
here, Triangle AOB
P stands for Perpendicular distance from Origin to line AB.
stands for the angle between the perpendicular and X-axis.
Its Equation is:-
\[x{\rm{ }}cos{\rm{ \theta}} + y{\rm{}}sin{\rm{ \theta}} = {\rm{ }}p\] Normal Form Formula
Polar Equation Of Straight Line:
It is called slope-intercept form. As we use a line’s slope and its intercept,
Look we have a general form of a line: ax + by = c
so, to use this equation in the polar form we transform it as \[y{\rm{ }} = {\rm{ }}r{\rm{ }}sin\theta \] and \[x{\rm{ }} = {\rm{ }}r{\rm{ }}cos\theta \].
The polar equation is –
\[\;{\bf{r}}({\bf{a}}{\rm{ }}{\bf{cos}}\theta + {\rm{ }}{\bf{b}}{\rm{ }}{\bf{sin}}\theta ) = {\rm{ }}{\bf{c}}\]
We can write polar forms as –
\[r\,\sin \theta + mr\,\,\cos \theta + c\]
Solved Examples
Question1: The given figure is an example of –
Line Segment
Perpendicular
Parallel lines
Ray
Ans: Line segment
Question2: Identify, which is the straight line –
Ans: 3 is the only one extending on both sides to infinity.
Solved Questions
Question 1: what is the general equation of line?
My = x + c
Y = mx + b
Sin x = 2 + ay
A = bx + c
[Hint: Y= mx + c]
Conclusion:
Till now we have learned about lines and the general form of it which is y = mx+c; we now know how to use a line in coordinate. And can derive any line equation from a given coordinate. Let’s have some practice on these concepts now.
FAQs on Normal Form of a Line in Coordinate Geometry
1. What is the normal form of a line in coordinate geometry?
The normal form of a line is the equation written as x cos θ + y sin θ = p, where p is the perpendicular distance from the origin to the line and θ is the angle made by the perpendicular with the positive x-axis.
- p ≥ 0 (shortest distance from origin to the line)
- θ is measured anticlockwise from the positive x-axis
- This form directly shows the geometric meaning of the line
2. What is the formula for the normal form of a line?
The formula for the normal form of a line is x cos θ + y sin θ = p.
- θ = angle between the perpendicular from the origin and the positive x-axis
- p = perpendicular distance of the line from the origin
3. How do you convert the general form of a line into normal form?
To convert the general form Ax + By + C = 0 into normal form, divide the entire equation by √(A² + B²).
- Step 1: Start with Ax + By + C = 0
- Step 2: Divide by √(A² + B²)
- Step 3: Rearrange into the form x cos θ + y sin θ = p
4. What does p represent in the normal form of a line?
In the normal form x cos θ + y sin θ = p, p represents the perpendicular distance of the line from the origin.
- It is always taken as a non-negative value
- It gives the shortest distance from (0,0) to the line
- If p = 0, the line passes through the origin
5. What does θ represent in the normal form of a line?
In the equation x cos θ + y sin θ = p, θ represents the angle made by the perpendicular from the origin to the line with the positive x-axis.
- Measured in anticlockwise direction
- Determines the orientation of the line
- Used to compute cos θ and sin θ values
6. Can you give an example of a line in normal form?
An example of a line in normal form is x cos 30° + y sin 30° = 5.
- cos 30° = √3/2
- sin 30° = 1/2
7. How is the normal form of a line different from the slope-intercept form?
The normal form x cos θ + y sin θ = p expresses a line using distance and angle, while the slope-intercept form y = mx + c uses slope and y-intercept.
- Normal form focuses on perpendicular distance from origin
- Slope-intercept form focuses on slope (m) and intercept (c)
- Normal form works even for vertical lines
8. How do you find the perpendicular distance from the origin using normal form?
The perpendicular distance from the origin is directly given by p in the normal form x cos θ + y sin θ = p.
- No calculation is needed once the equation is in normal form
- p represents the shortest distance from (0,0) to the line
9. Can every straight line be written in normal form?
Yes, every straight line can be expressed in the normal form x cos θ + y sin θ = p.
- Start with general form Ax + By + C = 0
- Divide by √(A² + B²)
- Adjust sign so that p ≥ 0
10. What are common mistakes when writing a line in normal form?
A common mistake in writing normal form is not dividing by √(A² + B²) correctly or forgetting to make p positive.
- Incorrect normalization of coefficients
- Wrong values of cos θ and sin θ
- Not adjusting sign when p is negative
