




Solved Examples: Multiplying Complex Numbers Explained
Complex numbers are very helpful in finding the square root of the negative numbers. Complex numbers have applications in many scientific research, fluid dynamics, vibration analysis, quantum mechanics, and electromagnetism. In this chapter, we are going to learn what a complex number is. How to multiply complex numbers and the Complex number differs from the Real number and Imaginary numbers. We will also learn to use methods for solving complex numbers.
What is a Complex Number?
A complex number is the summation of a real number and an imaginary number. A complex number is the form of a+ib, and it is usually represented by z. Here both a and b are real numbers. The value ‘a’ is called the real part, which is denoted by Re(z), and ‘b’ is called an imaginary part Im(z). Also, ib is also an imaginary number.
A combination of both the real and imaginary numbers is a complex number.
We know $i^2=-1$, let us calculate the value of 'i ' raised to the power.
Difference Between Complex Number, Real Number and Imaginary Number
To find out that what the difference amongst the three numbers refer to the table mentioned below:-
Multiplication of Complex Number
Multiplication of complex numbers or product of complex numbers is a procedure of the multiplication of two or more complex numbers by applying the distributive property. Mathematically, if we have two complex numbers, z = a + ib and w = c + id, then the multiplication of complex numbers z and w is written as zw = (a + ib) (c + id). Multiplying complex numbers is similar to multiplying polynomials. Polynomial identity is used to solve the multiplication of complex numbers: (a+b) (c+d) = ac + ad + bc + bd.
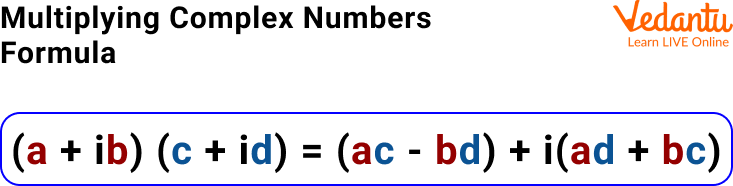
The formula for multiplying complex number is given as:
$(a+i b)(c+i d)=a c+i a d+i b c+i^2 b d,$ is
$(a+i b)(c+i d)=(a c-b d)+i(a d+b c)$.
Multiplying complex number
How to Multiply Complex Numbers?
When multiplying complex numbers, the most effective method is to use either FOIL method or the Distributive property to simplify the expressions. It also works when it is in need to multiply imaginary numbers. Following are the steps or stages which is used to multiply complex numbers by using the distributive property:-
Use the distributive property to multiply the real part of the first factor by the second factor.
Repeat step 1, but with the imaginary part of the first factor.
Combine like terms, as alike, with the algebraic expressions.
Simplify the complex number and express the final answer in the form $a+bi$ or $a-bi$
Example: $(-3+2i)(5-4i)$
Ans: $(-3+2i)(5-4i)$
$=-3(5-4i)+2i(5-4i)$
$=-15+12i+10i-8i^2$
$=22i-8i^2-15= -15+22i+8$
$=-7+22i$
Product of Two Complex Number
The product of two complex numbers can be expressed in the standard form A + iB where A and B are real.
Let $Z_1=p+i q$ and $Z_2=r+is$ is to be two complex numbers $(p, q, r$ and $s$ are real), then the product $Z_1 Z_2$ is defined as
$Z_1 Z_2=(p r-q s)+i(p s+q r)$
SUM of Complex Numbers
$(5-4 i)+(-2+6 i)=5-2-4 i+6 i$
$=3+2 i$
PRODUCT of Complex Numbers
$(5-4 i)+(-2+6 i)=-10+30 i+8 i-24 i^2$
$=-10+38 i-24(-1)$
$=-10+38 i+24$
$=14+38 i$
Multiplicative Inverse of Complex Numbers
The multiplicative inverse of a complex number on multiplying with the given complex number results in the multiplicative identity of 1 . The multiplicative inverse of the complex number $z=a+i b$ is $z^{-1}=\dfrac{\bar{z}}{|z|^2}$. Here $\bar{z}=a-i b$, and $|z|=\sqrt{a^2+b^2}$.
$z . z^{-1}=1$
$z^{-1}=\dfrac{\bar{z}}{|z|^2}$
For finding the multiplicative inverse of a complex number, we need the complex number's conjugate and the complex number's modulus. The conjugate of the complex number is $\bar{z}=a-i b$, and the modulus of the complex number is $|z|=\sqrt{a^2+b^2}$.
Let us take a simple example of finding the multiplicative inverse of a complex number $z=3+4 i$. For this complex number, the conjugate complex number is $\bar{z}=3-4 i$, and the modulus of the complex number is $|z|=\sqrt{3^2+4^2}=5$. And the multiplicative inverse is $z^{-1}=\dfrac{3-4 i}{5}=\dfrac{3}{5}- \dfrac{4 \mathrm{i}}{5}$.
Solved Examples
Q 1. Find the product of two complex numbers $(-2+\sqrt{3} i)$ and $(-3+2 \sqrt{3} i)$ and express the result in standard form $A+i B$.
Ans: $(-2+\sqrt{3 i})(-3+2 \sqrt{3 i})$
$=-2(-3+2 \sqrt{3} i)+\sqrt{3} i(-3+2 \sqrt{3} i)$
$=6-4 \sqrt{3} i-3 \sqrt{3} i+2(\sqrt{3} i)^2$
$=6-7 \sqrt{3} i-6$
$=6-6-7 \sqrt{3} i$
$=0-7 \sqrt{3} i$, which is the required from $A+iB$ where $A=0$ and $B=-7 \sqrt{3}$
Q 2. Multiply complex numbers $z=3-2 i$ and $w=-4+3 i$.
Ans: For multiplying complex numbers $z$ and $w$, we will use the formula $(a+i b)(c+i d)=(a c-b d)+i(a d+b c)$. Here $a=3, b$ $=-2, c=-4, d=3$
$(3-2 i)(-4+3 i)=[3 \times(-4)-(-2) \times 3)+i(3 \times 3+(-2) \times(-4))$ $=(-12+6)+i(9+8)$ $=-6+17 i$
$(3-2 \mathrm{i})(-4+3 \mathrm{i})=-6+17 \mathrm{i}$
Q 3. Find the square of the complex number $(-4+6 \mathrm{i})$.
Ans: To find the square of a complex number, we will use the formula $(a+i b)^2=\left(a^2-b^2\right)+i$ 2ab. Here, $a=-4$ and $b=6$
$(-4+6 i)^2=\left((-4)^2-6^2\right)+i 2 \times(-4) \times 6$
$=(16-36)-48 i$
$=-20-48 i$
$(-4+6 i)^2=-20-48 i$
Practice Questions
Q 1. The formula for multiplying complex numbers is:
$(a+i b)(c+i d)=(a c+b d)+i(a d+b c)$
$(a+i b)(c+i d)=(a c-b d)+i(a d+b c)$
$(a+i b)(c+i d)=(a c+b d)+i(b c+a d)$
$(a+i b)(c+i d)=(a b-c d)+i(a b+c d)$
Ans: (b)
$(a+i b)(c+i d)=(a c-b d)+i(a d+b c)$
Q 2. Find the multiplicative inverse of $\sqrt{2}+7 i$
Ans: $=\dfrac{\sqrt{2}}{51}-\dfrac{7}{51} i$
Q 3. Find the product of two complex numbers $(-2+\sqrt{3i})$ and $(-3+2 \sqrt{3i})$ and express the result in standard from $\mathrm{A}+\mathrm{iB}$.
Ans: $\mathrm{A}+\mathrm{iB}$, where $\mathrm{A}=0$ and $\mathrm{B}=-7 \sqrt{3}$
Summary
In contrast with real numbers, there is no natural ordering of the complex numbers. Specifically, there is no linear ordering on the complex numbers that is harmonious with addition and multiplication. Hence, the complex numbers do not carry the formation of an ordered field. Mathematically, a complex number is an element of the number system which extends to the real numbers with a specific element denoted 'i', which is known as the imaginary unit. Complex numbers allow solutions to all polynomial equations, even those that have no solutions in real numbers.
FAQs on How to Multiply Two Complex Numbers Easily
1. How do you calculate the multiplication of two complex numbers in standard form?
To multiply two complex numbers, for instance, z₁ = a + ib and z₂ = c + id, you apply the distributive property, similar to multiplying algebraic binomials. The resulting product is found by multiplying each term of the first complex number by each term of the second. The general formula is z₁z₂ = (ac - bd) + i(ad + bc). This formula arises from expanding (a + ib)(c + id) and simplifying, using the key property that i² = -1.
2. What are the fundamental properties that apply to the multiplication of complex numbers?
The multiplication of complex numbers adheres to several important properties that are consistent with real number arithmetic. These include:
Commutative Law: The order of multiplication does not affect the outcome (z₁z₂ = z₂z₁).
Associative Law: The grouping of numbers in a multiplication sequence does not change the result ((z₁z₂)z₃ = z₁(z₂z₃)).
Distributive Law: Multiplication is distributive over the addition of complex numbers (z₁(z₂ + z₃) = z₁z₂ + z₁z₃).
Multiplicative Identity: The number 1 (or 1 + 0i) is the multiplicative identity, as multiplying any complex number by 1 leaves it unchanged.
3. How is multiplying a complex number by a real number different from multiplying by another complex number?
When a complex number (a + ib) is multiplied by a real number 'k', the operation is a simple scaling. You distribute 'k' to both the real and imaginary parts: k(a + ib) = ka + i(kb). Geometrically, this scales the vector representing the complex number on the Argand plane but does not rotate it. Multiplying by another complex number, however, involves both scaling and rotation.
4. What is the method for multiplying two complex numbers in polar form?
Multiplying complex numbers in polar form is often more straightforward than in rectangular form. If you have two complex numbers z₁ = r₁(cos θ₁ + i sin θ₁) and z₂ = r₂(cos θ₂ + i sin θ₂), their product is found by multiplying their moduli (r) and adding their arguments (θ). The formula is: z₁z₂ = r₁r₂ [cos(θ₁ + θ₂) + i sin(θ₁ + θ₂)]. This clearly shows the resulting magnitude and angle of the product.
5. What is the geometric significance of multiplying two complex numbers?
The geometric interpretation of multiplying two complex numbers on an Argand plane is a combination of two distinct actions: rotation and scaling. When you multiply a complex number z₁ by another complex number z₂, the resulting vector for the product is achieved by rotating the vector of z₁ by the angle (argument) of z₂ and then scaling (stretching or shrinking) its length by the magnitude (modulus) of z₂.
6. Why does multiplying a complex number by its conjugate always result in a real number?
This is a crucial property used in complex number division. A complex number z = a + ib has a conjugate z̄ = a - ib. Their product is (a + ib)(a - ib). Using the difference of squares formula, this expands to a² - (ib)². Since i² = -1, the expression simplifies to a² - (-b²) = a² + b². This sum is always a non-negative real number and is equal to the square of the modulus of the complex number (|z|²). The imaginary parts effectively cancel each other out.
7. How is the concept of a multiplicative inverse applied to complex numbers?
The multiplicative inverse of a non-zero complex number z, denoted as z⁻¹, is the number that, when multiplied by z, results in the multiplicative identity, 1. In other words, z · z⁻¹ = 1. The inverse is found using the number's conjugate and modulus: z⁻¹ = z̄ / |z|². For z = a + ib, this translates to (a - ib) / (a² + b²). This concept is fundamental for defining division in the set of complex numbers.























