How To Multiply Fractions Step By Step With Formula And Examples
We know how important it is to learn about fractions because we often have their use in our daily lives. To understand fractions multiplications, knowing about their components and parts is necessary. What do a numerator and denominator denote, and what do portions mean? Multiplying fractions begins with the numerators multiplied, followed by the denominators multiplied. If necessary, the resultant fraction is simplified further and reduced to its simplest terms. So let’s head to learning in depth about the multiplication of fractions and how a number is to be multiplied by the given fraction.
Representation of Fraction
The first and most popular way to represent a fraction is in the form of the letter a/b. Here, a and b are referred to as the numerator and denominator, respectively. There is a line dividing the numerator and denominator.
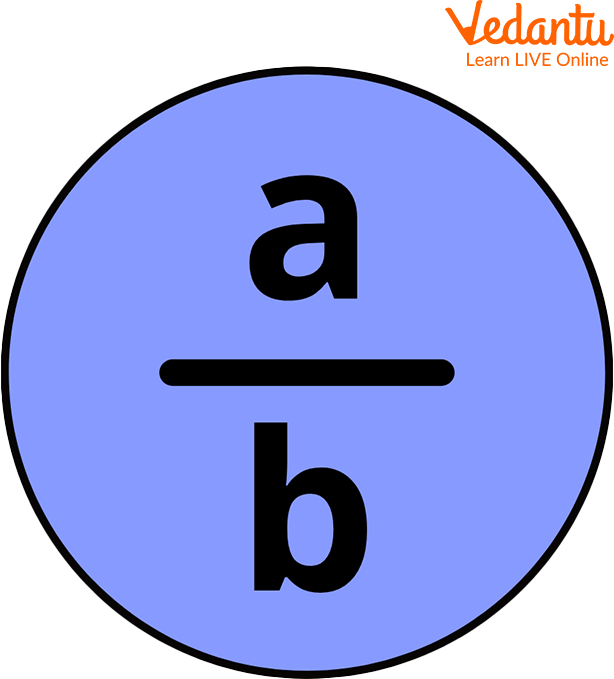
Representation of a Fraction
Types of Fraction
Proper Fraction: A fraction where the numerator is less than the denominator is known as a proper fraction.
i.e., Numerator < Denominator
Proper Fraction
Improper Fraction: A fraction where the numerator is greater than the denominator, then it is known as an improper fraction.
i.e., Numerator > Denominator
For example:
Improper Fraction
Mixed Fraction: A mixed fraction combines a natural number and a fraction. It is an improper fraction.
For example
Mixed Fraction
Multiplication of Fractions
In the multiplication of fractions, to multiply a fraction by one or more natural numbers or fractions, we will follow the following steps:
(i) Convert the natural numbers (if any) to improper fractions.
(ii) Convert the mixed numbers (if any) to improper fractions.
(iii) Multiply the numerator with the numerator and denominator with the denominator, cancel the common factors of the numerator and denominator and place the product of the numerator over the denominator.
(iv) Convert into a mixed fraction if needed.
Example: Multiply: $\dfrac{1}{3} \times \dfrac{3}{5}$
$\dfrac{1 \times 3}{3 \times 5}=\dfrac{3}{15}$
Now making $\dfrac{3}{15}$ into the simplest form, we will get
$=\dfrac{1}{5}$
$\therefore \dfrac{1}{3} \times \dfrac{3}{5}=\dfrac{1}{5}$
Product of two fractions = $\dfrac{\text{Product of their numerators}}{\text{Product of their denominators}}$
Solved Examples
Q1. A number is to be multiplied by the fraction $\dfrac{4}{5}$. But Samir, by mistake, multiplied it by $\dfrac{5}{4}$ and obtained the number 81 more than the correct one. What was the original number?
Ans: Let us assume that the number is $x$.
According to the question, on taking x common, the subtracting using LCM, we get
$\Rightarrow x \times \dfrac{5}{4} -x \times \dfrac{4}{5}=81$
Now on solving the above expression, we get
$\Rightarrow x \times\dfrac{25 - 16}{20}=81$
Now, by multiplying 81 by 20 and dividing by 9, we get
$\Rightarrow x \times \dfrac{9}{20}=81$
On Cancelling the common factors, we get
$\Rightarrow x=180$
Therefore the number is 180.
Q 2. What is $\dfrac{1}{2}$ of $\dfrac{10}{7}$ in fraction?
Ans: $\dfrac{1}{2}$ of $\dfrac{10}{7}$
$=\dfrac{1}{2} \times \dfrac{10}{7}$
(Find the common factor. Here it is 2 and 10).
After cancelling the common factors, you will get
$=1 \times \dfrac{5}{7}$
Therefore, the answer is $\dfrac{5}{7}$
Practice Problems
Q 1. Find the value of fraction A, if fraction A is thrice fraction B. The product of fractions A and B is $\dfrac{3}{49}$.
Ans: Fraction $B$ is $\dfrac{1}{7}$ and fraction $A$ is $\dfrac{3}{7}$
Q 2. What is $\dfrac{1}{2}$ of $\dfrac{3}{4}$ in fraction form?
Ans: $\dfrac{3}{8}$
Q 3. What will be the product of $\dfrac{5}{4} \times \dfrac{5}{2} \times \dfrac{5}{3}$?
Ans: $5 \dfrac{5}{24}$
Summary
We learned and understood the concept of fractions by knowing the use of its components and the calculations done with fractions terms. We also did some questions that made our concept understanding clearer and better. The first step is to multiply the two numerators. The second step is to multiply the two denominators. Finally, simplify the new fractions. The fractions can be simplified by factoring common factors in the numerator and denominator.
FAQs on Multiplication Of Fractions Explained With Steps
1. What is multiplication of fractions?
Multiplication of fractions is the process of multiplying the numerators together and the denominators together to get a new fraction. In simple terms, to multiply fractions:
- Multiply the numerators (top numbers).
- Multiply the denominators (bottom numbers).
For example, (2/3) × (4/5) = 8/15 because 2×4 = 8 and 3×5 = 15.
2. How do you multiply two fractions step by step?
To multiply two fractions, multiply the numerators together and multiply the denominators together. Follow these steps:
- Step 1: Multiply the numerators.
- Step 2: Multiply the denominators.
- Step 3: Simplify the result if possible.
Example: (3/4) × (5/6) = 15/24 = 5/8 after simplification.
3. What is the formula for multiplying fractions?
The formula for multiplying fractions is (a/b) × (c/d) = (a×c)/(b×d). Here:
- a and c are numerators.
- b and d are denominators (b ≠ 0, d ≠ 0).
This formula applies to proper, improper, and mixed fractions (after converting mixed numbers to improper fractions).
4. How do you multiply a fraction by a whole number?
To multiply a fraction by a whole number, multiply the numerator by the whole number and keep the denominator the same. You can also write the whole number as a fraction with denominator 1.
- Write 4 as 4/1.
- Example: (2/5) × 4 = (2/5) × (4/1) = 8/5.
You may convert the improper fraction 8/5 to a mixed number: 1 3/5.
5. How do you multiply mixed fractions?
To multiply mixed fractions, first convert them into improper fractions, then multiply normally. Steps:
- Convert mixed numbers to improper fractions.
- Multiply numerators and denominators.
- Simplify the result.
Example: 1 1/2 × 2 1/3 = (3/2) × (7/3) = 21/6 = 7/2 or 3 1/2.
6. Do you need a common denominator to multiply fractions?
No, you do not need a common denominator to multiply fractions. Unlike addition or subtraction of fractions, multiplication only requires multiplying numerators and denominators directly.
- Addition/subtraction → common denominator needed.
- Multiplication → no common denominator required.
Example: (1/2) × (3/7) = 3/14 without finding a common denominator.
7. How do you simplify before multiplying fractions?
You simplify before multiplying fractions by cross-canceling common factors between a numerator and a denominator. This method reduces numbers before multiplication.
- Find common factors between diagonally opposite numbers.
- Divide both by their common factor.
- Then multiply the reduced numbers.
Example: (4/9) × (3/8). Cancel 4 and 8 by 4 → 1 and 2; cancel 3 and 9 by 3 → 1 and 3. Result = 1/6.
8. What happens when you multiply fractions with different denominators?
When multiplying fractions with different denominators, you simply multiply across without changing the denominators first. The denominators are multiplied together as they are.
- Example: (2/3) × (5/4).
- Multiply numerators: 2×5 = 10.
- Multiply denominators: 3×4 = 12.
Result = 10/12 = 5/6 after simplification.
9. Why does multiplying by a fraction less than 1 make the number smaller?
Multiplying by a fraction less than 1 makes a number smaller because you are taking only a part of that number. A fraction less than 1 represents a portion.
- Example: 8 × (1/2) = 4.
- Example: 10 × (3/4) = 7.5.
Since the fraction is less than 1, the product is less than the original number.
10. What are common mistakes when multiplying fractions?
Common mistakes when multiplying fractions include adding numerators and denominators instead of multiplying and forgetting to simplify. Key errors to avoid:
- Adding across: (1/2) × (1/3) ≠ 2/5.
- Not converting mixed numbers to improper fractions.
- Forgetting to simplify the final answer.
Correct example: (1/2) × (1/3) = 1/6.
