




How to Find and Use Intercepts in Linear Equations
What is the Intercept of a Line?
The x-intercept and the y-intercept are the two different types of intercepts. The line's actual point of intersection with the x-axis is known as the x-intercept, while its actual point of intersection with the y-axis is known as the y-intercept. In this article, we will define the intercept, show how to obtain the intercept for a given line, and demonstrate how to graph intercepts.
What is x-Intercept?
The general form of the linear equation is written as \[y = mx + c\], where m and c are constants. The line's crossing point, which is located at the x-axis of the plane, is known as the x-intercept. This indicates that anytime a linear equation crosses the x-axis, its y-coordinate value will always be equal to 0. The y-coordinate is zero for the x-intercept and the x-coordinate is zero for the y-intercept. The term "horizontal intercept" also applies to the x-intercept.
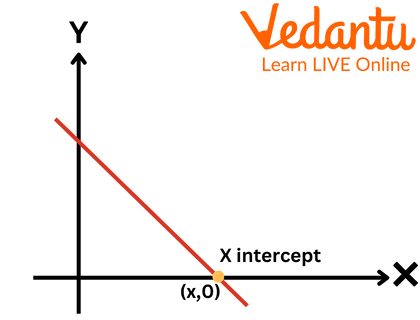
X-Intercept
What is y- Intercept?
The graph's intersection with the y-axis is known as the y-intercept. Finding the intercepts for any function with the formula \[y = f\left( x \right)\] is crucial when graphing the function. An intercept can be one of two different forms for a function. The x-intercept and the y-intercept are what they are. A function's intercept is the location on the axis where the function's graph crosses it.
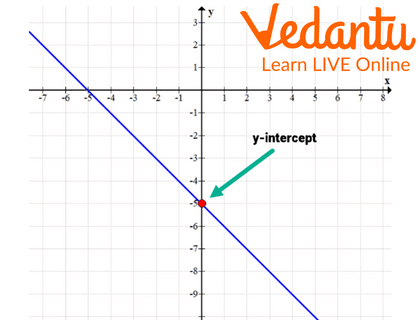
Y-Intercept
Equation of a Line with Intercepts
How to find an intercept of a straight line? Intercepts are subject to various equations and formulas. By solving for x and putting \[y = 0\] in the equation, all of the formulas are obtained.
Following are the steps to determine the y intercept of a function, where\[y = f\left( x \right)\], where \[x = 0\] is simply substituted.
Resolve for y.
Put the y-point intercepts in place (0, y).
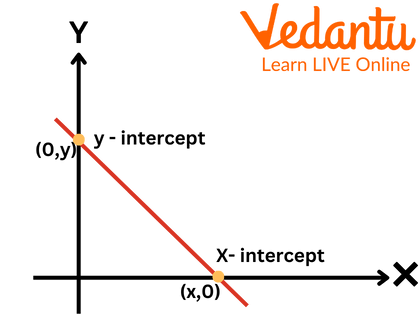
Intercepts
Conclusion
The two different kinds of intercepts are the x-intercept and the y-intercept. The x-intercept of a line is its actual point of intersection with the x-axis, and the y-intercept is its true point of intersection with the y-axis.
Solved Examples
Example 1:Find the value of "a" if the y-intercept of a function \[y = a(x - 1)\left( {x - 2} \right)\left( {x - 3} \right)\] is \[\left( {0,12} \right)\] .
Ans: The given function's equation is:
\[y = a(x - 1)\left( {x - 2} \right)\left( {x - 3} \right)\]
By adding \[x = 0\] to the y-intercept formula, it can be calculated.
\[y = a \left( {0 - 1} \right]\left[ {0 - 2} \right]\left[ {0 - 3} \right]\] \[ = - 6a\]
The y-intercept is therefore \[\left( {0, - 6a} \right)\]
However, the issue claims that the provided function's y-intercept is \[\left( {0,12} \right)\]. Thus,
\[ - 6a = 12\]
Using -6 to divide both sides,
\[a = - 2\]
Example 2: Find the x and y intercept in the given graph.
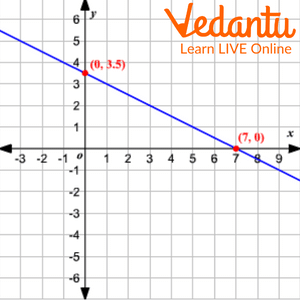
Ans: The x-intercept is 7 and y – intercept is 3.5 in the given graph.
Example 3: Find the x-intercept of \[y = 4x - 8\].
Ans: For finding the x – intercept we must put y coordinate as 0.
Thus, putting\[y = 0\] ,we will get:
\[\begin{array}{l}0 = 4x - 8\\8 = 4x\\x = 2\end{array}\]
Therefore, x coordinate is 2.
FAQs on Intercepts of a Line Explained for Students
1. What are the intercepts of a line in coordinate geometry?
In coordinate geometry, the intercepts of a line are the points where the line crosses the coordinate axes.
- The x-intercept is the point where the line intersects the x-axis. At this point, the y-coordinate is always zero, giving a point of the form (a, 0).
- The y-intercept is the point where the line intersects the y-axis. At this point, the x-coordinate is always zero, giving a point of the form (0, b).
2. How do you find the x-intercept and y-intercept of a line from its general equation (Ax + By + C = 0)?
To find the intercepts from the general form of a line's equation, you can follow a simple two-step process:
- To find the x-intercept, substitute y = 0 into the equation and solve for x. The equation becomes Ax + C = 0, so x = -C/A. The x-intercept point is (-C/A, 0).
- To find the y-intercept, substitute x = 0 into the equation and solve for y. The equation becomes By + C = 0, so y = -C/B. The y-intercept point is (0, -C/B).
3. What is the intercept form of a straight line's equation?
The intercept form of a straight line's equation is written as x/a + y/b = 1. This form is particularly useful because the values 'a' and 'b' directly represent the intercepts of the line.
- 'a' is the x-intercept (the line crosses the x-axis at (a, 0)).
- 'b' is the y-intercept (the line crosses the y-axis at (0, b)).
4. How can you determine the intercepts from the slope-intercept form (y = mx + c)?
In the slope-intercept form, y = mx + c, the intercepts can be found as follows:
- The y-intercept is given directly by the constant term 'c'. The coordinate of the y-intercept is (0, c).
- To find the x-intercept, you set y = 0 and solve for x. This gives 0 = mx + c, which rearranges to mx = -c, so x = -c/m. The coordinate of the x-intercept is (-c/m, 0), provided the slope 'm' is not zero.
5. Why are the intercepts of a line considered important concepts in mathematics?
Intercepts are crucial for several reasons beyond just finding points on a graph.
- Practical Application: In real-world models, the y-intercept often represents an initial value or starting condition (e.g., the initial cost in a business problem), while the x-intercept can represent a break-even point or end condition.
- Efficient Graphing: Finding the two intercepts provides the quickest way to accurately plot a straight line on a Cartesian plane.
- Geometric Calculations: The intercepts are used to calculate the area of the triangle formed by the line and the coordinate axes, a common problem in geometry.
6. What does it signify if a line has only one intercept or no intercepts at all?
These are special cases that describe the line's orientation:
- One Intercept: A line has only one unique intercept if it passes through the origin (0, 0). In this case, both the x-intercept and y-intercept are at the same point.
- Horizontal Lines: A horizontal line like y = k (where k ≠ 0) has a y-intercept at (0, k) but is parallel to the x-axis, so it has no x-intercept.
- Vertical Lines: A vertical line like x = h (where h ≠ 0) has an x-intercept at (h, 0) but is parallel to the y-axis, so it has no y-intercept.
7. Can a line have an x-intercept of 0? What does this imply?
Yes, a line can have an x-intercept of 0. An x-intercept of 0 means the line crosses the x-axis at the point where x=0. This point, (0, y), is by definition on the y-axis. For the line to cross both axes at the same single point, that point must be the origin (0, 0). Therefore, if the x-intercept is 0, the y-intercept must also be 0. This implies the line's equation is of the form y = mx, representing a line that passes directly through the origin.
8. How do the signs (+/-) of the x and y-intercepts describe a line's position on a graph?
The signs of the intercepts tell you which quadrants the line segment between them occupies and give a clue about the line's slope.
- Positive x-intercept & Positive y-intercept: The line passes through the 1st quadrant and has a negative slope.
- Negative x-intercept & Positive y-intercept: The line passes through the 2nd quadrant and has a positive slope.
- Negative x-intercept & Negative y-intercept: The line passes through the 3rd quadrant and has a negative slope.
- Positive x-intercept & Negative y-intercept: The line passes through the 4th quadrant and has a positive slope.























