Getting to Know the Intercept Form of a Line

The intercept form of a line equation is \[\dfrac{x}{a} + \dfrac{y}{b} = 1\] . This is one of the most significant types of line equations. In addition, the sign of the intercepts in this equation tells us where the line is in relation to the coordinate axes. The intercept form of the line equation may be regarded as the line that forms a right triangle with the coordinate axes, with the sides having lengths as 'a' and 'b' units, respectively.

What is Intercept?

A one-dimensional geometrical form is a line. In general, a line can be represented as a planar figure in a coordinate plane. In the cartesian coordinate system, the coordinate plane has two perpendicular axes termed the horizontal X-axis and the vertical Y-axis. You might be wondering what is intercept in maths. The intercepts are the spots where the line intersects the two axes. In Math, the x-intercept definition is given by the point of intersection of the line with the X-axis, while the y-intercept definition is given by the point of intersection of the line with the Y-axis.

What is the Intercept Form of a Line?

The intercept form of a line equation has the equation\[\dfrac{x}{a} + \dfrac{y}{b} = 1\], where 'a' is the x-intercept and 'b' is the y-intercept. The x-intercept is the smallest distance from the origin to a point on the x-axis where the line cuts the x-axis, and the y-intercept is the shortest distance from the origin to a point on the y-axis where the line cuts the y-axis. Taking into account the points, the line cuts the x-axis at point (a, 0) and the y-axis at point (0, b).

Equation of Intercept Form of a Line

Intercept line equation form: \[\dfrac{x}{a} + \dfrac{y}{b} = 1\]

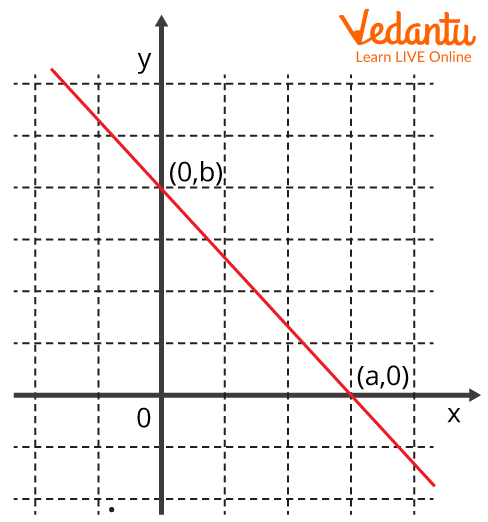
Graph Showing The Intercepts At X And Y Axis

Here, x and y are the variables in the equation, while a and b are the x and y intercepts. The slope of this equation is \[\dfrac{{ - b}}{a}\]. Because this line intersects both coordinate axes, it forms a right triangle with them, and the area of the right-angled triangle is the product of half of its intercepts \[\dfrac{1}{2}\left| {ab} \right|\]. Furthermore, the intercept form of a line's equation may be reduced and expressed as the standard form of a line's equation as \[bx + ay = ab\].

Proof for Intercept Form of the Equation of a Line

Consider the line in the picture above that intersects the X and Y axes at positions a and b. The coordinates of the line's intersection with the X-axis are represented as P \[[{x_1},{y_1}]\] \[ = \] (a, 0). Similarly, the line's point of intersection with the Y-axis is given as Q \[[{x_2},{y_2}]\] \[ = \] (0, b). The equation of a line with two points is as follows.

\[\dfrac{{y - {y_1}}}{{{y_2} - {y_1}}} = \dfrac{{x - {x_1}}}{{{x_2} - {x_1}}}\]

Putting the value of \[{x_1},{x_2},{y_1}\]and \[{y_2}\] in the above equation.

\[\begin{array}{l}\dfrac{{y - 0}}{{b - 0}} = \dfrac{{x - a}}{{0 - a}}\\\dfrac{y}{b} = \dfrac{{x - a}}{{ - a}}\\\dfrac{y}{b} = \dfrac{x}{a} + \dfrac{{ - a}}{{ - a}}\\\dfrac{y}{b} + \dfrac{x}{a} = 1\end{array}\]

The above equation is the equation for the intercept form of a straight line.

Facts About the Intercept of the Line

• The y coordinate is 0 at the point where the line intersects the X-axis. So, the X intercept is obtained by inserting y = 0 in the line equation.

• The x coordinate is 0 at the point where a line intersects the Y-axis. As a result, the 'y' coordinate is the value of y at the position (0, y) on the line. In Math, this is the definition of the y-intercept.

• We can determine the quadrants in which the line travels based on the sign of the intercepts.

• With the coordinate axes, the intercept form of the line equation forms a right triangle, and the area of this right triangle is \[\dfrac{1}{2}\left| {a.b} \right|\].

Sample Questions

1. The intercept of a line can be seen in the shape of

1. Square

2. Rectangle

3. Square

4. Circle

Ans. Triangle

2. What would be the X-intercept if the line cuts the X-axis at P and Y-axis at Q?

1. (P, 0)

2. (0, P)

3. (Q, 0)

4. (0, Q)

Ans. (P, 0)

3. What would be the Y-intercept if the line cuts the X-axis at P and Y-axis at Q?

1. (P, 0)

2. (0, P)

3. (Q, 0)

4. (0, Q)

Ans. (0, Q)

Conclusion

The intercept form of a line is a line that intersects or cuts the x and the y axis at different points. These points of intersection are labelled as a and b. The area of the triangle formed by the line and the two axes can be found using the formula.