




Key Properties and Pro Tips for Drawing Parallelograms
If you're struggling with geometry, don't worry. With this step-by-step guide, you'll be able to know how to make a parallelogram or construct it in no time! Just remember the basic definition of a parallelogram - It is a special kind of quadrilateral that is formed by parallel lines. The angle between the adjacent sides of a parallelogram may vary, but the opposite sides need to be parallel for it to be a parallelogram.
So, it can also be said that a parallelogram is a quadrilateral. A parallelogram has two pairs of parallel lines, called the bases, while the other pair is a set of diagonals that intersect at their midpoints. In this article, we will look at parallelograms and how to draw a parallelogram.
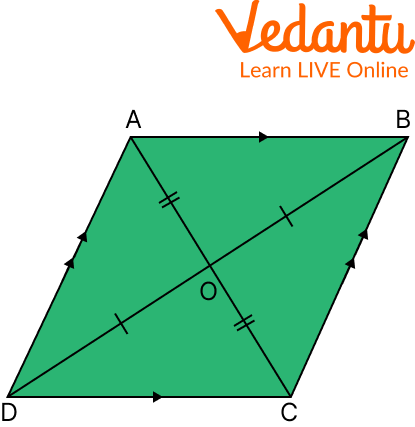
Parallelogram
Properties of a Parallelogram
Following are the Properties of a Parallelogram:
A parallelogram can be identified using certain simple properties. Examine the following parallelogram PQTR in relation to the properties listed below.
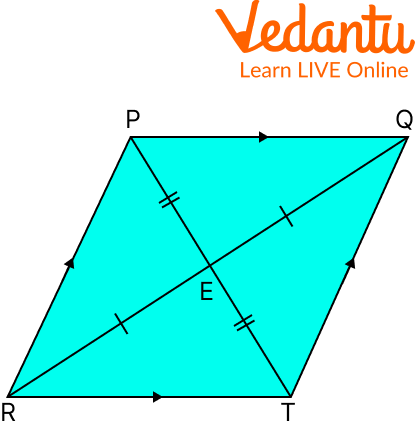
Parallelogram PQTR
The following properties can help us identify and differentiate a parallelogram:
The opposite sides of a parallelogram are parallel. Here, $PQ \| RT$ and $PR \| Q T$.
The opposite sides of a parallelogram are equal. Here, $P Q=R T$ and $P R=QT$
The opposite angles of a parallelogram are equal. Here, $\angle P=\angle T$ and $\angle Q=\angle R$
The diagonals of a parallelogram bisect each other. Here, RE = EQ and $P E=E T$
Same-side interior angles supplement each other. Here, $\angle P R T+$ $\angle R T Q=180^{\circ}, \angle R T Q+\angle T Q P=180^{\circ}, \angle T Q P+\angle Q P R=180^{\circ}, \angle Q P R+$ $\angle P R T=180^{\circ}$
The diagonals divide the parallelogram into two congruent triangles. Here, $\triangle \mathrm{RPQ}$ is congruent to $\triangle \mathrm{RTQ}$, and $\triangle \mathrm{RPT}$ is congruent to $\triangle Q T P$
Parallelogram is a Quadrilateral
A quadrilateral with two opposite pairs of parallel sides is known as a parallelogram. A parallelogram's opposite sides are equal in length, and its opposite angles are equal in size. Furthermore, the interior angles on the same transversal side are additional. And that is why we call a parallelogram a quadrilateral.
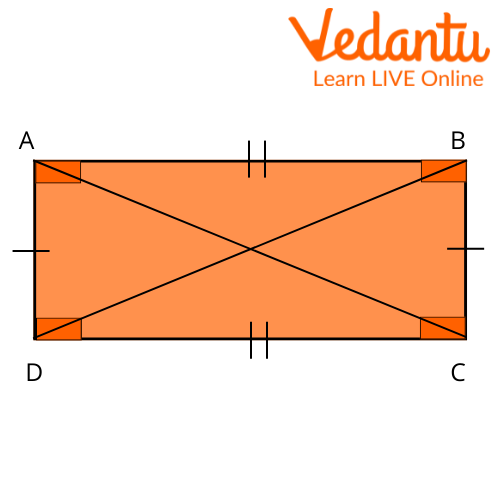
Quadrilateral ABCD
Can a Square be a Parallelogram?
A parallelogram having four equal sides and four right angles is called a square.
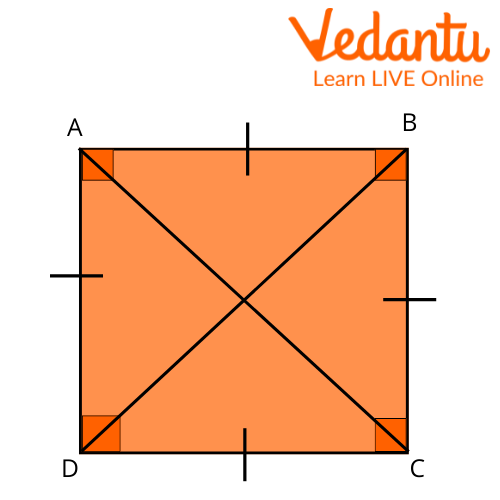
Square ABCD
Examine the square ABCD to see how it relates to the following qualities. A square contains:
Four equal sides. Here, $A B=B C=C D=D A$
Four right angles. Here, $\angle \mathrm{A}=\angle \mathrm{B}=\angle \mathrm{C}=\angle \mathrm{D}=90^{\circ}$
Two pairs of parallel sides. Here, $A B \| D C$ and $A D|| B C$
Two equal diagonals. Here, $A C=B D$
Diagonals that are perpendicular to each other. Here, $A C \perp B D$
Diagonals that bisect each other.
Therefore, from the above properties, it can be said that a square is a parallelogram.
Construct a Parallelogram
Construct a Parallelogram When Two Consecutive Sides and the Included Angle are given:
Step 1: Construct a line segment $A B=4 \mathrm{~cm}$.
Step 2: Construct a 60-degree angle at point $A$.
Step 3: Construct a line segment $A D=5 \mathrm{~cm}$ on the other arm of the angle.
Step 4: Then, place the sharp point of $5 \mathrm{~cm}$ above $B$
Step 5: Stretch your compasses to $4 \mathrm{~cm}$, place the sharp end at D and draw an arc to intersect the arc drawn in step 2.

Draw a Parallelogram
Step 6: Label the intersecting point $C$.
Step 7: Join $C$ to $D$ and $B$ to $C$ to form the parallelogram $A B C D$.
Practice Problems
Q 1. Construct a parallelogram whose diagonal is 5.4 cm and 6.2 and an angle between them is 70.
Q 2. Construct a parallelogram when one of its side is $4 \mathrm{~cm}$ and its two diagonal are $5.6 \mathrm{~cm}$ and $7 \mathrm{~cm}$. Measure the other side.
Summary
A parallelogram is a four-sided figure with two pairs of parallel sides. Then we saw the properties of a parallelogram, and we came to know that a square is a parallelogram. To construct a parallelogram, you will need a scale and a compass.
First, use the compass to draw two arcs that intersect at two points. Then, use the scale to connect the points of intersection. Finally, use the compass to draw two more arcs that intersect at two additional points. Connect these points as well, and you will have created a parallelogram. We have now seen how to construct a parallelogram given certain conditions.
FAQs on Step-by-Step Guide: Constructing a Parallelogram
1. What is a parallelogram in geometry?
A parallelogram is a special type of quadrilateral, which is a four-sided polygon. It is defined as a flat shape with two pairs of parallel sides. This means the opposite sides are parallel to each other and will never intersect, no matter how far they are extended.
2. What are the fundamental properties of a parallelogram?
A parallelogram has several key properties that are essential for its construction and for solving problems related to it. The main properties are:
Opposite sides are equal: The lengths of opposite sides are always the same.
Opposite sides are parallel: This is the defining characteristic of a parallelogram.
Opposite angles are equal: The angles at opposite vertices are congruent (have the same measure).
Consecutive angles are supplementary: Any two angles next to each other add up to 180 degrees.
Diagonals bisect each other: The two diagonals intersect at their midpoint, dividing each other into two equal halves.
3. What are the basic tools required to construct a parallelogram?
To accurately construct a parallelogram, you will need a few basic geometry tools. These include:
A ruler or a straightedge for drawing line segments of precise lengths.
A compass for drawing arcs to mark equal lengths and locate vertices.
A protractor to measure and draw angles accurately.
A sharpened pencil for drawing clean lines.
4. What are the basic steps to construct a parallelogram if two adjacent sides and the angle between them are known?
To construct a parallelogram, for instance ABCD, where you know the lengths of adjacent sides AB and BC and the angle ∠B, you can follow these steps:
Step 1: Draw a line segment AB of the given length using a ruler.
Step 2: At point B, use a protractor to measure and draw the given angle. Draw a ray extending from B along this angle.
Step 3: With B as the centre, use a compass to cut an arc with a radius equal to the length of BC on the ray. Mark this point of intersection as C.
Step 4: Using the property that opposite sides are equal, set your compass to the length of BC and draw an arc from point A. Then, set your compass to the length of AB and draw an arc from point C. The point where these two arcs intersect is D.
Step 5: Join points A to D and C to D to complete the parallelogram ABCD.
5. What are some examples of parallelograms in real life?
Parallelograms are common in our surroundings. Some real-world examples include the top surface of many desks and tables, the shape of building blocks, the pattern on some tiled floors, and the typical shape of an eraser. The leaning shape of the Eiffel Tower's base also forms a parallelogram.
6. Why are all rectangles considered parallelograms, but not all parallelograms are rectangles?
This is because of their specific properties. A rectangle qualifies as a parallelogram because it meets the fundamental definition: it has two pairs of parallel sides. However, a rectangle has an additional, stricter condition that all its interior angles must be right angles (90°). A general parallelogram does not need to have 90° angles. Therefore, every rectangle is a special type of parallelogram, but a parallelogram only becomes a rectangle if its angles are all right angles.
7. How is a trapezoid (or trapezium) different from a parallelogram?
The key difference lies in the number of parallel sides. A parallelogram must have exactly two pairs of opposite sides that are parallel. In contrast, a trapezoid has only one pair of opposite parallel sides. This is why a trapezoid does not share all the properties of a parallelogram, such as opposite sides and opposite angles being equal.
8. Can you construct a unique parallelogram if you only know the lengths of its two diagonals? Why or why not?
No, it is not possible to construct a unique parallelogram if only the lengths of its two diagonals are given. While the diagonals of a parallelogram must bisect each other (cross at their midpoints), the angle at which they intersect is not fixed. You can create an infinite number of different parallelograms by changing this intersection angle, leading to shapes ranging from a tall rhombus to a wide, flat parallelogram, all with the same diagonal lengths.
9. What is the main difference between constructing a parallelogram and a rhombus?
The main difference relates to side lengths. For a general parallelogram, you only need to ensure that opposite sides are equal in length. For a rhombus, which is a special type of parallelogram, you must ensure that all four sides are equal in length. This stricter condition for a rhombus often simplifies its construction, as you only need one side length and one angle to define it.

















