




Key Properties and Types of Parallelograms Explained
In two dimensions, a parallelogram is a geometric shape with parallel sides. It has two parallel sides that are of the same length, making it a four-sided polygon (sometimes referred to as a quadrilateral). The sum of the adjacent angles of a parallelogram is 180 degrees.
Parallelograms are a unique class of polygons. It is a quadrilateral in which the opposite sides of both pairs are parallel. A parallelogram's characteristics make it simple and quick to distinguish between several given shapes.
The word "parallelogram," which means "bounded by parallel lines," is derived from the Greek word "parallelogramma". Let's find out more about parallelograms, their characteristics, and some examples.
Concept of a Parallelogram
Having two sets of parallel sides makes a quadrilateral a parallelogram.
A parallelogram has opposite sides that are the same length and angles that are of the same measure.
Additionally, the internal angles on the transverse side are supplementary. The total internal angles add up to $360^\circ $.
A parallelepiped is a three-dimensional shape with faces that are parallelograms.
The area of a parallelogram is given by its base, which is one of its parallel sides, and height, which is the difference between its top and bottom heights. The lengths of a parallelogram's four sides determine the perimeter of that parallelogram.
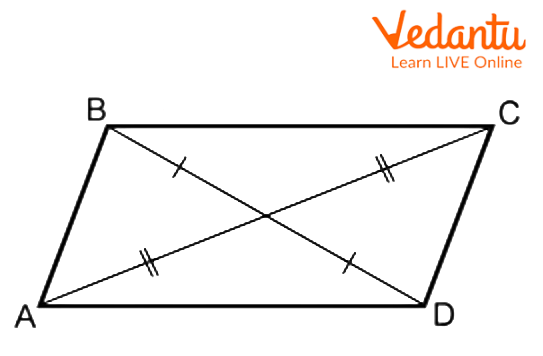
Parallelogram ABCD with Equal Diagonals
As you can see from the previous figure, ABCD is a parallelogram where $AB\parallel CD$ and $AD\parallel BC$.
Furthermore, $AB = CD$ and $AD = BC$ .
In addition, $\angle A = \angle C$ & $\angle B = \angle D$ .
$\angle A$ and $\angle D$ are supplementary angles as well because they are located on the same side of the transversal. The additional angles $\angle B$ and $\angle C$ function similarly.
Consequently, $\angle A + \angle D = 180^\circ $, $\angle B + \angle C = 180^\circ $.
Shape of a Parallelogram
A parallelogram has two dimensions. Each of its four sides has two parallel pairs of sides. Additionally, the parallel sides have the same length. If the parallel sides are not equal, the shape is not a parallelogram. Similarly to this, a parallelogram must always have equal inner angles on both sides. Otherwise, the given shape will not be a parallelogram.
Some Special Types of Parallelograms
Square and Rectangle: Two forms that resemble a parallelogram in terms of its characteristics are the square and the rectangle. Both have their opposing sides parallel to and equal to one another. Both squares and rectangles have diagonals that bisect each other in two equal halves.
Rhombus: If all of a parallelogram's sides are congruent or equal to one another, the parallelogram is a rhombus.
Rhomboid: This is a unique type of parallelogram with opposite sides that are parallel to one another but the neighbouring sides are of different lengths. The angles are also all 90 degrees.
Trapezium: If there are two parallel sides and two non-parallel sides, the shape will be a trapezium.
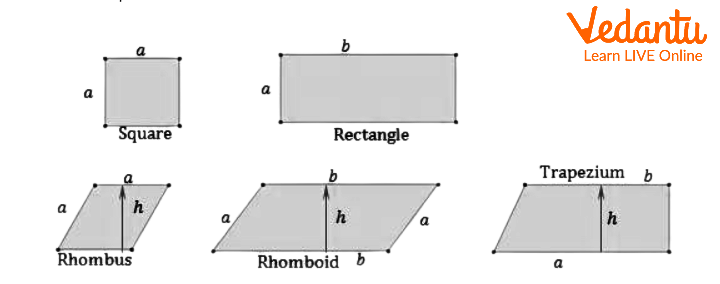
Different Types of Parallelograms
What Are the Properties of a Parallelogram?
A quadrilateral is a special type of polygon, which can be known as a parallelogram if it contains two parallel opposite sides. A parallelogram has the following properties:
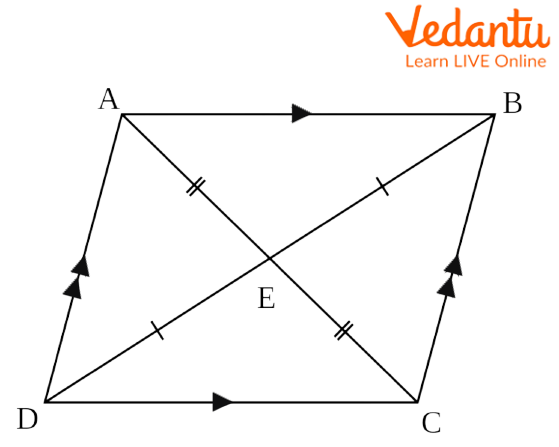
Properties of a Parallelogram
The opposing sides are congruent and parallel. Segment AB is parallel and congruent to segment DC, while segment AD is parallel and congruent to segment BC.
The opposing angles show congruency. Angle A is congruent with angle C, while angle D is congruent with angle B.
Consecutive interior angles on the same side have a supplementary sum. Angles A and D are supplementary, as angles B and C. Similarly, angles A and B, angles D and C.
All of the angles will be at right angles if any one of them is a right angle.
Each of the two diagonals intersects the other diagonal.
A parallelogram can be divided into two congruent triangles by each of its diagonals. Triangle DCB and triangle DAB are congruent.
Formulas for Area and Perimeter of a Parallelogram
The next section discusses the formula for a parallelogram's area and perimeter. These equations can be used by students to solve difficulties.
Parallelogram's Area
A parallelogram's area is the area that it takes up in a two-dimensional plane. The formula to calculate the parallelogram area is listed below:
Base x Height = Area
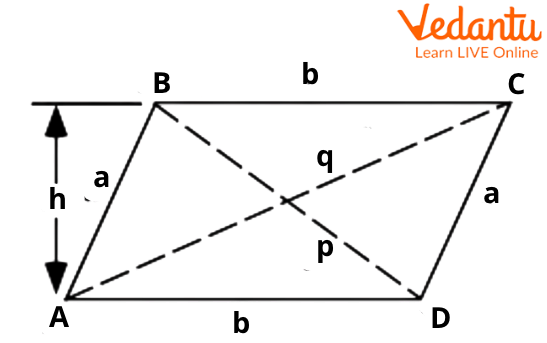
Parallelogram
Parallelogram's Perimeter
The sum of the distances between the parallelogram's boundaries equals its perimeter. We must be aware of the length and width measurements in order to determine the perimeter value. The parallelogram's opposing sides are of equal length. In order to compute the perimeter, the following formula is used:
Perimeter $ = 2(a + b)$ units.
where the parallelogram's side lengths are $a$ and $b$.
Solved Examples
Q.1. The quadrilateral ABCD has an AB value of $8.5$ units. ABCD's diagonals are right angles to one another. Determine ABCD's perimeter.
Solution. A quadrilateral is a rhombus if its diagonals intersect at right angles, as determined by the characteristics of parallelograms.
Therefore, ABCD is a rhombus, and $AB = BC = CD = DA$ follows.
The perimeter then equals $4 \times AB = 4 \times 8.5 = 34$ units.
Q.2. Determine the area of a parallelogram with a $5$cm base and an $8$ cm height.
Solution. The base is $5$ cm, and the height is $8$ cm.
Knowing that Area = Base x Height
Area $ = 5 \times 8$
Area $ = 40$sq. cm
So, the area is $40$sq.cm
Practice Questions
A parallelogram with sides of $20$ and $15$ metres has a diagonal of length $15$ metres. What is the area of such a parallelogram?
Find the area of a parallelogram whose adjacent sides are $15$ cm and $8$ cm.
Answers
$100\sqrt 5 $ sq. m
$46$ sq. cm
Summary
The learning outcomes from the parallelogram topic will help in properly understanding all the geometric shapes related to a parallelogram, how to determine a parallelogram's area and perimeter, and examples of where we might see a parallelogram in daily life. In this article, we have undertaken an in-depth study of the geometrical figure, parallelogram and also discussed its properties. Do try to solve the examples and practice questions provided above to enhance your understanding of the topic further.
List of Related Articles
FAQs on What Is a Parallelogram?
1. What is a parallelogram in geometry?
A parallelogram is a special type of quadrilateral, which is a four-sided polygon. The defining characteristic of a parallelogram is that it has two pairs of opposite sides that are parallel to each other. This fundamental property leads to all its other unique characteristics.
2. What are the essential properties used to identify a parallelogram?
A quadrilateral can be identified as a parallelogram if it satisfies any one of the following conditions:
Both pairs of opposite sides are parallel (this is the definition).
Both pairs of opposite sides are equal in length.
Both pairs of opposite angles are equal in measure.
The diagonals bisect each other, meaning they intersect at their midpoints.
One pair of opposite sides is both equal and parallel.
3. How do you calculate the area and perimeter of a parallelogram?
The formulas to calculate the area and perimeter are fundamental for solving problems related to parallelograms:
Area of a Parallelogram: The formula is Area = Base × Height. Here, the 'base' is the length of one of the sides, and the 'height' is the perpendicular distance from that base to the opposite side.
Perimeter of a Parallelogram: The formula is Perimeter = 2 × (a + b), where 'a' and 'b' are the lengths of the two adjacent sides. Since opposite sides are equal, you just need to sum the lengths of two adjacent sides and multiply by two.
4. What is the difference between a parallelogram and a general quadrilateral?
While every parallelogram is a quadrilateral, not every quadrilateral is a parallelogram. A quadrilateral is any polygon with four sides. A parallelogram is a specific type of quadrilateral that must meet the strict condition of having two pairs of parallel opposite sides. For example, a trapezium (which has only one pair of parallel sides) and a kite are quadrilaterals but not parallelograms because they do not satisfy this condition.
5. Are the diagonals of a parallelogram always equal?
No, the diagonals of a parallelogram are not always equal. While they always bisect each other (cut each other into two equal halves), their total lengths are only equal in special types of parallelograms like a rectangle and a square. In a general parallelogram or a rhombus, one diagonal will be longer than the other.
6. What are the main types of parallelograms?
There are three special types of parallelograms, each with additional properties:
Rectangle: A parallelogram where all four interior angles are right angles (90°).
Rhombus: A parallelogram where all four sides are equal in length.
Square: A parallelogram that is both a rectangle and a rhombus. It has four equal sides and four right angles.
7. Can a rectangle be considered a parallelogram? Why?
Yes, a rectangle is always a parallelogram. This is because it fits the primary definition of a parallelogram: its opposite sides are parallel. A rectangle is simply a more specific version of a parallelogram that also has the additional property of all its angles being 90 degrees. Therefore, a rectangle inherits all the properties of a parallelogram, including opposite sides being equal and diagonals bisecting each other.
8. What are some real-world examples of a parallelogram?
Parallelograms are found in many man-made structures and natural patterns. Some common examples include:
The tops of many desks and tables.
The shape of most building bricks and floor tiles.
The side faces of a leaning box or a stack of books pushed sideways.
Structural designs in bridges and architectural trusses for stability.
The basic shape of many erasers.
9. Why is it important to understand the properties of a parallelogram?
Understanding the properties of a parallelogram is crucial as it is a foundational concept in geometry. This knowledge is essential for:
Solving complex geometric problems and proofs in higher classes.
Understanding concepts in other fields like vector physics, where the 'Parallelogram Law of Vector Addition' is used to find the resultant of two vectors.
Applications in engineering and architecture, where the rigidity and predictable angles of parallelograms are used to design stable and strong structures.























