Must-Know Geometry Words Every Student Should Understand
A branch of mathematics that studies the sizes, shapes, positions, angles and dimensions of 2D and 3D figures is called Geometry. Shapes like squares, circles, and triangles are a part of flat geometry and they are 2-D. However, shapes like spheres, cylinders, cubes, cuboids, and so on are 3-D. Each shape that we study in geometry has specific properties and these properties.
So, let us learn about the various geometric shapes and their appearance. Following this, we will go through the meaning of each property of a geometric shape with a specific definition.
What are 2-D Shapes in Geometry?
Shapes that have only two dimensions, i.e., length and width are 2-D shapes. Below, you can find 2-D shapes:
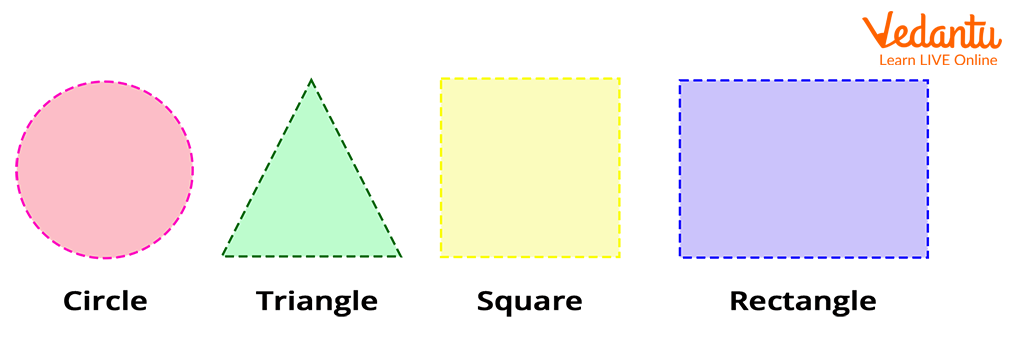
2-D Shapes
What are 3-D Shapes in Geometry?
Shapes that have three dimensions, i.e., length, width, and height are 3-D shapes. Below, you can find 3-D shapes:

3-D Shapes
All these shapes have respective parameters like a triangle has three edges, vertices, and angles. A cuboid has length, width, and height. Now, a question arises: what are these parameters? Well, all these terms come under Geometry Vocabulary and what does this vocabulary mean? Let us understand.
Various Terms in Geometry
So, this was all about the geometry vocabulary. Going through this will help you understand what parameters does a geometrical shape has.
FAQs on Geometry Vocabulary Explained: Terms, Meanings & Uses
1. What is meant by 'geometry vocabulary'?
Geometry vocabulary refers to the specific set of terms and definitions used to describe, measure, and analyse shapes, sizes, positions of figures, and properties of space. Just like any language, this vocabulary provides the fundamental words like point, line, angle, and polygon, which are essential for understanding and communicating geometric concepts accurately.
2. What are the three fundamental undefined terms in geometry and why are they important?
The three fundamental undefined terms in geometry are the point, line, and plane. They are considered undefined because they are so basic that they can only be explained through examples and descriptions. Their importance lies in the fact that they are the foundational building blocks from which all other geometric figures and concepts, known as defined terms, are constructed.
3. How are defined terms like 'line segment', 'ray', and 'angle' built upon undefined terms?
Defined terms are created using the undefined terms (point, line, plane) as a foundation. For example:
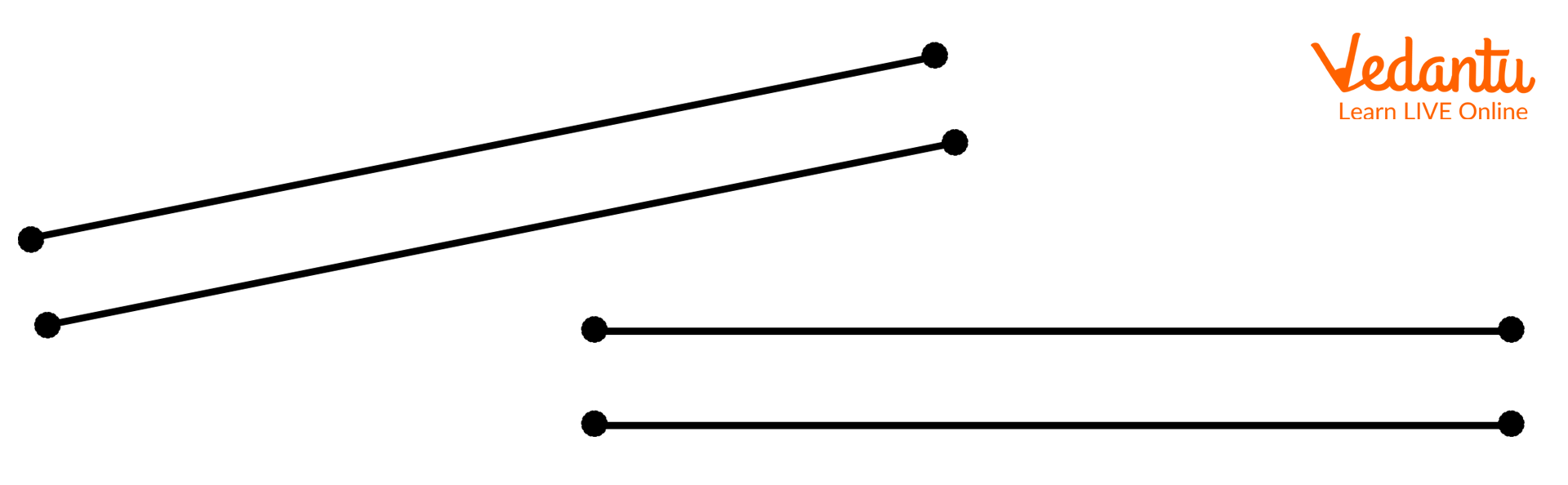
- A line segment is a part of a line that is bounded by two distinct end points.
- A ray is also a part of a line which has one starting point and extends infinitely in one direction.
- An angle is formed by two rays that share a common endpoint, which is called the vertex of the angle.
4. What is the main difference between intersecting lines and parallel lines?
The main difference lies in whether they meet. Intersecting lines are two or more lines that cross each other at a single, common point. In contrast, parallel lines are two lines on the same plane that are always the same distance apart and never meet, no matter how far they are extended.
5. What defines a polygon, and can you provide some examples?
A polygon is a flat, two-dimensional shape that is fully closed and made up of three or more straight line segments. These segments are joined end-to-end, and each segment touches exactly two other segments at its endpoints. Common examples of polygons include:
- Triangle: A polygon with 3 sides.
- Quadrilateral: A polygon with 4 sides.
- Pentagon: A polygon with 5 sides.
- Hexagon: A polygon with 6 sides.
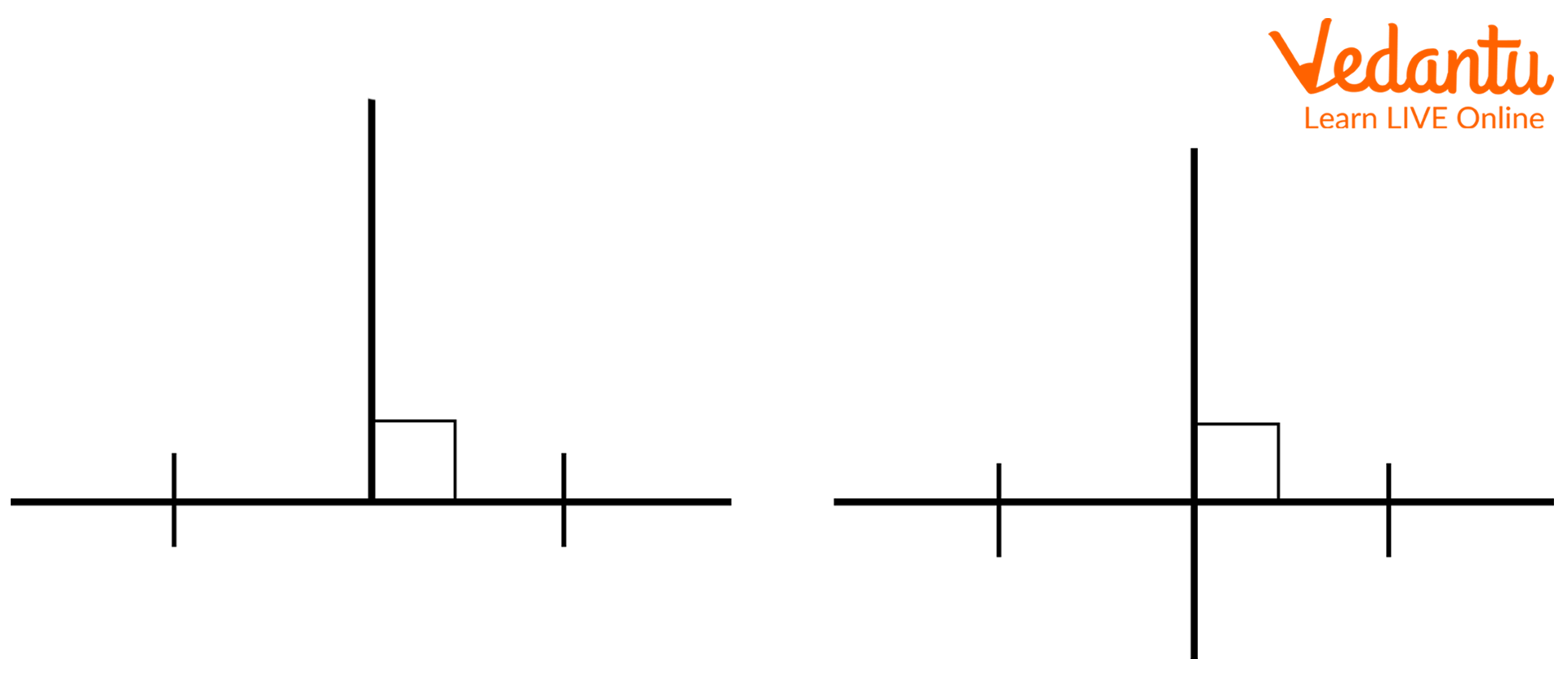
6. How are the different types of angles classified based on their measurements?
Angles are classified based on their degree measure. The primary types are:
- Acute Angle: An angle that measures less than 90 degrees.
- Right Angle: An angle that measures exactly 90 degrees.
- Obtuse Angle: An angle that measures greater than 90 degrees but less than 180 degrees.
- Straight Angle: An angle that measures exactly 180 degrees, forming a straight line.
7. Why is it important to distinguish between a 'simple curve' and a 'closed curve'?
Distinguishing between these curves helps classify shapes more accurately. A simple curve is one that does not cross itself. A closed curve is one that has no endpoints and encloses an area. The distinction is important because a shape like a circle is both simple and closed, whereas a figure-eight is a closed curve but it is not simple because it intersects itself. Understanding this helps define the boundaries of polygons and other complex shapes.
8. What are the basic components that define a circle?
A circle is defined by several key components, all related to its centre point. The basic components are:
- Centre: The fixed point inside the circle from which all points on the circle are equidistant.
- Radius: The distance from the centre to any point on the circle.
- Diameter: A straight line segment that passes through the centre and whose endpoints lie on the circle. It is the longest chord and is equal to twice the radius.
- Chord: A line segment whose endpoints both lie on the circle.
- Circumference: The total distance around the boundary of the circle.