




How to Convert Fractions: Methods & Practice Questions
When a complete item is divided into equal pieces, each component is referred to as a fraction. A fraction, in other terms, is a portion of the total. A fraction is composed of two parts: the numerator and the denominator. It is written as a numerator/denominator. The numerator indicates how many total factors are taken, whereas the denominator indicates the total number of equal parts.
What is a Mixed Fraction?
Improper fractions are represented more simply using mixed numbers. Improper Fraction: Do you know what it is? A fraction is referred to be an improper fraction if it cannot be further simplified and has a numerator that is more than or equal to the denominator. A mixed fraction is one generated by mixing a whole number and a fraction. Conversion of fraction example: if 3 is a whole number and \[\dfrac{5}{9}\] is the fraction part then, \[3\dfrac{5}{9}\] is the mixed fraction.
Conversion of Improper Fraction Into a Mixed Fraction(Mixed Number Converter)
An improper fraction has a numerator greater than a denominator. In order to convert this fraction into a mixed fraction, we can follow the following steps.
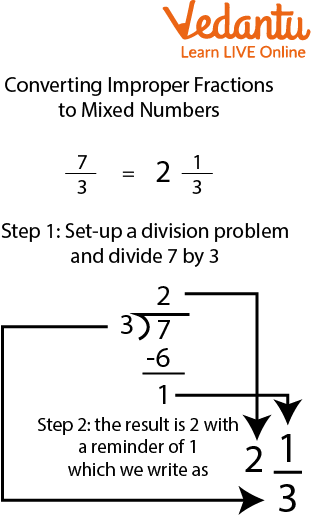
Step one- Divide the fraction (numerator divided by denominator)
Step two- Obtain the remainder.
Step three- The whole number part of the mixed fraction would be the quotient obtained after dividing and the numerator part will be the remainder, which we got in step two. In this, the denominator(divisor) will remain the same.
Example – \[\dfrac{12}{5}\] will have 2 as a remainder and 2 as the quotient. So, the mixed fraction would be \[2\dfrac{2}{5}\].
Converting Improper Fraction to Mixed Fraction
Conversion of Mixed Fraction Into an Improper Fraction
The mixed fraction can be changed easily into an improper fraction by following the given steps.
Step one- Multiple the denominator with the whole number part of the equation.
Step two- The product obtained will then be added to the numerator of the given mixed fraction.
Step three- The result we got would be the numerator of the improper fraction and the denominator would remain.
Example- \[7\dfrac{2}{3}\] in this mixed fraction we will multiply 3 and 7 and the product we will get is 21 which will then be added to 2 giving the result as 23. So, the improper fraction will turn out as \[\dfrac{23}{3}\].
Methods of Reduction of Different Fractions
The methods through which the complex fraction can be changed into the simplest form so that it further can be divided. There are different methods by which the fraction can be reduced. By dividing the numerator and denominator by a common divisor until the common factor equals 1, we may simplify fractions by reducing them. To put it another way, a fraction can only be divided by 1 or another whole integer. Consider the fraction 8/24 as an illustration. Here is how to decrease the fraction step by step.
Step 1: Write the denominator and numerator's factors in Step 1. The factors of 24 are 1, 2, 3, 4, 6, 8, 12, and 24 while the factors of 8 are 1, 2, 4, and 8.
Step 2: The second step is to identify the shared factors between the numerator and the denominator. 1, 2, 4, and 8 are the factors that 8 and 24 have in common.
Step 3: Subtract the common factors from the numerator and denominator until there is only one common factor remaining: 1. This gives you the fraction in its reduced form.
Let's start dividing by 2: \[\dfrac{{8}}{{24}} = \dfrac{{8 \div 2}}{{24 \div 2}} = \dfrac{4}{12}\]. We will continue to divide by 2 until we can't go any further. So, we have \[\dfrac{{4 \div 2}}{{12 \div 2}} = \dfrac{2}{6} = \dfrac{{2 \div 2}}{{6 \div 2}} = \dfrac{1}{3}\].
Therefore, the reduced form of \[\dfrac{8}{{24}}\]is \[\dfrac{1}{{3}}\].
Tips for Reducing Fractions
So you now understand the different methods for reducing a fraction to its simplest form. Here are some tips to assist you in fast-reducing fractions. When reducing fractions to their simplest form, use these techniques.
If a fraction's numerator or denominator is a prime number, the fraction cannot be simplified anymore.
A fraction with 1 in the numerator cannot be further lowered.
To simplify an improper fraction, first, express it as a mixed fraction and then simplify it as you would a proper fraction.
For application of any arithmetic operation convert into like fraction so that they have the same denominator.
Sample Questions
1) Convert \[4\dfrac{1}{3}\] into an improper fraction.
Ans)
The first step is to multiply the denominator by the whole number component of the equation.
Step two is to add the resulting product to the numerator of the current mixed fraction.
Step three- the outcome would be the improper fraction's numerator and the denominator would remain.
\[\begin{array}{l}4\dfrac{1}{3} = 3 \times 4 + 1 = 13\\ = \dfrac{{13}}{3}\end{array}\]
2) Convert \[\dfrac{16}{5}\] into a mixed fraction.
Ans)
Step one: divide the numerator by the denominator
Step two: get the remainder
Step three: The quotient produced after dividing the whole number component of the mixed fraction will be the numerator part, which we received in step two. The denominator (divisor) will remain constant in this case.
\[\dfrac{{16}}{5} = 16 \div 5 = 3\]
Remainder = 1
Fraction \[3\dfrac{1}{5}\]
3) Add \[1\dfrac{3}{4}\] and \[2\dfrac{5}{6}\].
Ans)
Convert the mixed fraction into an improper fraction.
As the denominators are different, take LCM and make the denominator the same.
Now add the numerator.
\[\begin{array}{l}1\dfrac{3}{4} = \dfrac{7}{4}\\2\dfrac{5}{6} = \dfrac{{17}}{6}\end{array}\]
LCM of 4 and 6 is 12.
\[\dfrac{{21}}{{12}} + \dfrac{{34}}{{12}} = \dfrac{{55}}{{12}}\]
4) Multiply \[3\dfrac{4}{7}\] and \[4\dfrac{5}{9}\] .
Ans) Convert the mixed fraction into an improper fraction and then multiply the numerators and denominators separately.
\[\begin{array}{l}3\dfrac{4}{7} = \dfrac{{25}}{7}\\4\dfrac{5}{9} = \dfrac{{41}}{9}\\\dfrac{{25}}{7} \times \dfrac{{41}}{9} = \dfrac{{1025}}{{63}}\end{array}\]
5) Reduce the fraction \[\dfrac{18}{81}\] by GCF method.
Ans) As the highest common factor is 9 for the given fraction, it needs to be divided by 9 to reduce it.
\[\begin{array}{l}\dfrac{{18}}{{81}}\\ = 18 \div 9,81 \div 9\\ = \dfrac{2}{9}\end{array}\]
6) Reduce the following fractions by the GCF method. a) 16/64, b) 18/81
Solution: We will use the GCF method to reduce fractions.
a) The greatest common factor of 16 and 64 is 16. Dividing the numerator and the denominator by 16, we get the fraction reduced to \[\dfrac{1}{4}\].
\[\dfrac{{16}}{{64}} = \dfrac{{16 \div 16}}{{64 \div 16}} = \dfrac{1}{4}\]
Therefore, the reduced form of \[\dfrac{{16}}{{64}}\] is \[\dfrac{1}{4}\]
b) The greatest common factor of 18 and 81 is 9. Dividing the numerator and the denominator by 9, we get the fraction reduced to \[\dfrac{2}{9}\]
\[\dfrac{{18}}{{81}} = \dfrac{{19 \div 9}}{{81 \div 9}} = \dfrac{2}{9}\]
Therefore, the reduced form of \[\dfrac{{18}}{{81}}\] is \[\dfrac{2}{9}\].
Conclusion
A fraction consists of a numerator and a denominator. The fraction can be like a fraction, unlike fractions and mixed fractions. The mixed fraction can be converted into an improper fraction or unlike fraction and vice versa. Like fraction is a fraction whose denominator is the same and is greater than the numerator.
FAQs on Fraction Conversion Made Easy
1. What are the most common types of fraction conversions taught in the CBSE syllabus?
In Maths, fraction conversion primarily involves changing a fraction's form without altering its value. The main conversions are:
- Fraction to Decimal: Dividing the numerator by the denominator (e.g., 1/4 becomes 0.25).
- Decimal to Fraction: Placing the decimal value over a power of ten and simplifying (e.g., 0.5 becomes 5/10, which simplifies to 1/2).
- Improper Fraction to Mixed Fraction: Dividing the numerator by the denominator to find the whole number and the remainder (e.g., 7/3 becomes 2 1/3).
- Mixed Fraction to Improper Fraction: Multiplying the whole number by the denominator and adding the numerator (e.g., 2 1/3 becomes (2*3+1)/3 = 7/3).
- Simplifying Fractions: Reducing a fraction to its lowest terms by dividing the numerator and denominator by their highest common factor (HCF).
2. What is the step-by-step method to convert a fraction to its simplest form?
To convert a fraction to its simplest or lowest form, you need to find a common number that can divide both the numerator and the denominator. The standard method is as follows:
- Find the Highest Common Factor (HCF): Identify the largest number that divides both the numerator and the denominator without leaving a remainder. For the fraction 12/18, the factors of 12 are 1, 2, 3, 4, 6, 12 and the factors of 18 are 1, 2, 3, 6, 9, 18. The HCF is 6.
- Divide Both Parts: Divide both the numerator and the denominator by the HCF.
- Write the Simplified Fraction: The new fraction is the simplified form. For our example: 12 ÷ 6 = 2 and 18 ÷ 6 = 3. Therefore, the simplest form of 12/18 is 2/3.
3. How do you convert a decimal number like 0.75 into a fraction?
Converting a decimal into a fraction is a straightforward process based on place value. Here are the steps using 0.75 as an example:
- Step 1: Write the decimal as a fraction with a denominator of 1. So, 0.75 becomes 0.75/1.
- Step 2: Multiply both the numerator and the denominator by a power of 10 to eliminate the decimal point. Since 0.75 has two digits after the decimal, we multiply by 100. This gives (0.75 x 100) / (1 x 100) = 75/100.
- Step 3: Simplify the resulting fraction to its lowest terms. The highest common factor (HCF) of 75 and 100 is 25. Dividing both by 25 gives 75 ÷ 25 = 3 and 100 ÷ 25 = 4. The final fraction is 3/4.
4. Why is it mathematically impossible for a fraction to have zero as its denominator?
A fraction represents division; the numerator is divided by the denominator. The denominator tells us how many equal parts a whole has been divided into. For example, 1/4 means one whole is divided into four equal parts. If the denominator is zero, as in 4/0, it implies dividing a whole into zero parts. This is a logically and mathematically impossible action. Division by zero is undefined in mathematics because it does not yield a meaningful, computable value. Therefore, any fraction with a denominator of zero is considered meaningless.
5. What is the main difference between proper, improper, and mixed fractions?
The main difference lies in the relationship between the numerator and the denominator, which determines the fraction's value relative to one whole.
- Proper Fraction: The numerator is smaller than the denominator (e.g., 3/5). Its value is always less than 1.
- Improper Fraction: The numerator is greater than or equal to the denominator (e.g., 8/5). Its value is always 1 or more.
- Mixed Fraction: It is a combination of a whole number and a proper fraction (e.g., 1 3/5). It's another way to write an improper fraction and clearly shows the number of wholes contained within it.
6. How does converting an improper fraction to a mixed fraction help in understanding its real-world value?
Converting an improper fraction to a mixed fraction makes its value more intuitive and easier to visualize in real-world scenarios. For example, if a recipe calls for 7/2 cups of flour, it's hard to measure directly. By converting 7/2 to the mixed fraction 3 1/2, you immediately understand it means 3 full cups and one half cup. This conversion translates an abstract mathematical value into a concrete, measurable quantity, making it easier to compare sizes, measure ingredients, or place the value on a number line accurately.
7. When converting fractions, how are decimals and percentages related?
Decimals and percentages are two different ways of representing a fraction, and they are directly related. A decimal represents a fraction whose denominator is a power of 10 (e.g., 1/2 = 0.5, which is 5/10). A percentage is a special type of fraction where the denominator is always 100. The conversion process highlights their link:
- To convert a fraction to a decimal, you divide the numerator by the denominator (e.g., 3/4 = 0.75).
- To get the percentage, you take that decimal result and multiply by 100 (e.g., 0.75 x 100 = 75%).

















