




How to Find and Use the Factors of 161 in Maths
Factors of a number is defined as the integers that completely and evenly divide the given number without leaving any remainder. Given a number, we can write it into a product of its factors. This is known as the factorization of a number. The factors are the numbers which are always smaller than or equal to the given number and divide the number exactly.
Definition of Factor
A factor of a number is another number that divides the given number without leaving any remainder. It means that we can add finite copies of a factor together to get the original number. For example, 2 is divisible by 1 and 2. So, factors of 2 are 1 and 2.
How to Find factors of 161?
Given the number 161, we know there are at least two factors of a number: 1 and the number itself. So, two of the factors of 161 are 1 and 161. To find the remaining factors, we start dividing 161 by 2, 3, 4, … up to 160(as the factors are always less than or equal to the given number).
We find that 7 is the first prime that divides 161, and the quotient is 23. So, 7 and 23 are the factors of 161. Next, we need to check up to 23 only because for numbers greater than 23; if the number divides 161, the quotient must be less than 7, which is not possible in this case.
Next, we divide 161 by 8; the remainder is not zero. So, 8 doesn’t divide 161. Similarly, 9, 10, 11, and 22 do not divide 161. 23 dividends, 161 evenly. Thus, the next prime, which divides 161, is 23. Hence, we get the factors of 161 as 1,7,23 and 161.
Since 161 is an integer, thus the factors of 161 will include both positive and negative factors as: 1, -1, 7, -7, 23, -23, 161, -161.
Prime Factors of 161
Prime numbers have only two factors, i.e., 1 and the number itself. The factors of 161 are 1,7,23, and 161. Out of these, the prime numbers are 7 and 23. So, the prime factors of 161 are 7 and 23.
Considering 161 as an integer, the prime factors of 161 will be 7, 23.
Prime Factorization of 161
To find the prime factorisation of 161, find the prime factors of 161. Recall that Prime Numbers are those which have only two factors: 1 and the number itself. Out of 1,7,23,161, the prime numbers are 7 and 23.
So, the prime factors of 161 are 7,23 and \[7 \times 23 = 161\].
Prime Factorization of 161 is \[7 \times 161\].
We can do this in another way:
Start from 2(prime number). Is\[161 \div 2\]? NO.
The next prime is 3. Is\[161 \div 3\]? NO.
Is \[161 \div 5\]? NO.
Is \[161 \div 7\]? YES.
Write 7 to the left of 161 and\[161 \div 7\], i.e., 23 below 161.
We continue till we get 1 at the end.
Next, do it for 23. Since 23 is a prime number,\[23 \div 23 = 1\].
Now, write the numbers in the left column in the form of multiplication as \[161=7\times23\].
This is the prime factorisation of 161.
If we consider 161 as an integer, then we can write the prime factorisation of 161 as\[\left( { - 7} \right) \times \left( { - 23} \right)\].
Formula for Number of Positive Factors
Given prime factorisation of a number is \[m = {x_1}^{{a_1}}{x_2}^{{a_2}} \ldots {x_n}^{{a_n}}\]
Where \[{x_1},{x_2}, \ldots ,{x_n}\] are prime numbers and \[{a_1},{a_2}, \ldots ,{a_n}\] are powers of primes. Then number of positive factors \[N = ({a_1} + 1)({a_2} + 1) \ldots ({a_n} + 1)\].
Here, \[m = 161\].
Prime Factorization of 161 is \[161 = {7^1} \times {23^1}\].
Here, \[{a_1} = 1,{a_2} = 1\]. So, the number of Factors of 161
\[\begin{array}{l}N = ({a_1} + 1)({a_2} + 1)\\ = (1 + 1)(1 + 1)\\ = (2)(2)\\ = 4\end{array}\]
Hence, the number of positive factors of 161 are 4.
Prime Factorization of 161 Using Factor Tree
Factor trees is a way of expressing the factorisation of a number in terms of its prime factors. It uses repeated division by prime numbers to get the prime factorisation.
All the branches of the tree are split into factors. When the factors at the end are prime numbers, we stop. Writing them in multiplicative form gives the prime factorisation of 161.
We start dividing the number by prime numbers and write the number and the quotient as the tree branches. This process is repeated till we get all the prime numbers at the end. This is represented as
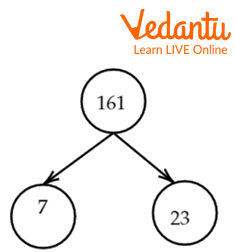
Factor tree of 161
So, the prime factorization of 161 is \[7\times23\].
Factors of 161 in Pairs
To write all the factors of 161 in pairs, we see that
\[1\times 161=161\]
\[7\times23=161\]
\[23\times7=161\]
\[161\times 1=161\]
So, writing the numbers on the left-hand side in pairs, we get (1,161), (3,23) are the factors of 161 in pairs. Considering negative factors, we get (-1,-161), (-7,-23) as the factor pairs of 161.
Solved Examples
Q1. What is the sum of prime factors of 161?
Solution: The factorization of 161 is
The prime factors of 161 are 7 and 23.
The sum of prime factors of 161 is 23+7 =30.
Q2. What is the sum of negative factors of 161?
Solution: The factorization of 161 is
The positive factors of 161 are 1, 7, 23, 161.
The negative factors of 161 are -1, -7, -23, -161.
The sum of negative factors is -1+( -7)+( -23)+( -161) =-192.
Q3. What are factor pairs of 71?
Solution: The factorization of 71 is
The factors of 71 are 1,71.
All factors of 71 are 1,71,-1,-71.
The factor pairs are (1,71) and (-1,-71).
Interesting Facts
Product of two prime numbers is a composite number.
Sum all factors of a number is always zero.
Key Features
To find the factors of 161, we can use a factor tree.
The factors of 161 are 1, 7, 23, 161 and their negative counterparts.
The factor pairs of 161 are\[1 \times 161\], \[7 \times 23\], \[( - 1) \times ( - 161)\]and \[( - 7) \times ( - 23)\].
Conclusion
The factors of 161 are 1,7,23,161,-1,-7,-23,-161.
The prime factors of 161 are 7 and 23.
The factor pairs of 161 are (1,161),(-1,-161),(7,23), (-7,-23).
List of Related Articles
Practice Questions
1. Find the prime factors of 100.
Answer: The prime factors of 100 are 2,5.
2. What is the prime factorization of 65?
Answer: The prime factorization of 65 are \[5\times17\].
FAQs on Factors of 161 Explained with Examples
1. What are the factors of 161?
The factors of 161 are the numbers that divide it completely without leaving any remainder. The factors of 161 are 1, 7, 23, and 161.
2. Is 161 a prime or a composite number?
The number 161 is a composite number. A number is classified as composite if it has more than two factors (i.e., factors other than 1 and itself). Since 161 has four factors (1, 7, 23, 161), it is not a prime number.
3. How do you find the prime factors of 161?
To find the prime factors of 161, you can use the prime factorization method. You start by dividing 161 by the smallest prime numbers. We find that 161 ÷ 7 = 23. Since both 7 and 23 are prime numbers, the process stops here. Therefore, the prime factorization of 161 is 7 × 23, and its prime factors are 7 and 23.
4. What are the factor pairs of 161?
Factor pairs of 161 are the pairs of numbers that, when multiplied together, result in 161. The positive factor pairs for 161 are:
- 1 × 161
- 7 × 23
Additionally, there are negative factor pairs, such as (-1) × (-161) and (-7) × (-23).
5. What is the difference between the factors and multiples of 161?
Factors and multiples are distinct concepts in mathematics:
- Factors are numbers that divide 161 exactly. The factors of 161 are finite and are 1, 7, 23, and 161.
- Multiples are the results of multiplying 161 by an integer (like 1, 2, 3, ...). The multiples of 161 are infinite. For example, the first three multiples are 161, 322, and 483.
6. Why is checking for divisibility only up to the square root of a number a useful method to test for prime numbers?
When checking if a number like 161 is prime, you only need to test for divisibility by prime numbers up to its square root (which is approx. 12.7). This is an efficient shortcut because if a number has a factor larger than its square root, it must also have a corresponding factor that is smaller. By testing the primes 2, 3, 5, 7, and 11, we find that 7 divides 161. This immediately confirms 161 is a composite number without needing to test any further.
7. How can we find the Highest Common Factor (HCF) of 161 and another number, like 42?
To find the Highest Common Factor (HCF) of 161 and 42, you should list the factors for both numbers:
- Factors of 161: 1, 7, 23, 161
- Factors of 42: 1, 2, 3, 6, 7, 14, 21, 42
Next, identify the factors that are common to both lists. Here, the common factors are 1 and 7. The HCF is the largest of these common factors, which is 7.

















