Division of Mixed Fractions

Let's start with an example You and your friend ate a whole pizza, and a quarter of a Let's start with an example You and your friend ate a whole pizza and a quarter of a pizza. As a mixed fraction, we can write this as 1 and $\dfrac{1}{4}$. A fraction consists of an integer, and a real fraction is called a mixed number. Example $6 \dfrac{4}{5}, 9 \dfrac{2}{3}$. A mixed fraction division is a division operation performed between two mixed fractions. In this article, you will learn how to divide mixed fractions with the help of examples.

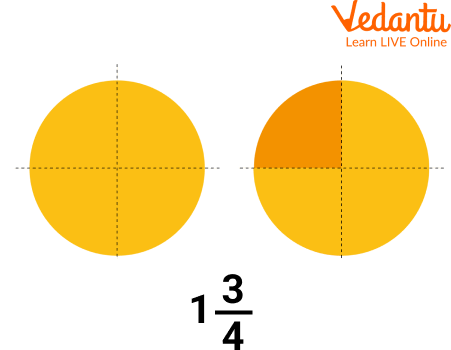
The pictorial representation of the Mixed fraction

Dividing Mixed Fractions

A mixed fraction division is a division operation performed between two mixed fractions. It is similar to the multiplication operation in that it takes the reciprocal of the second fraction.

Dividing Mixed Fractions with Like Denominators

As you know, the term "same denominator" means that the denominators are the same. To understand the procedure with an example, consider mixed numbers with the same denominator.

Let's look at the following key points to help you divide mixed numbers.

• The mixed fraction $a \dfrac{b}{c}$ can also be written $a+\left(\dfrac{b}{c}\right)$ and vice versa.

• To convert a mixed number to an improper fraction, multiply the integer by the denominator and add the result to the numerator of the proper fraction. The denominator remains the same. For example, to convert $3 \dfrac{1}{6}$ to an improper function, we multiply 6 and 3, i.e., $3 \times 6=18$, and the result is added to 1, i.e., $18+$ $1=19$. Thus the improper fraction is $\dfrac{19}{6}$

• To convert an improper fraction to a mixed fraction, divide the numerator of the improper fraction by the denominator. The quotient becomes the integer part, the remainder becomes the numerator of the appropriate fraction, and the denominator remains unchanged. For example, to convert $\dfrac{21}{4}$ to a mixed number, we first divide 21 by 4 and get the quotient as 5 and the remainder as 1 . Thus, the mixed fraction is $5 \dfrac{1}{4}$

Now, let's see an example of how to divide mixed fraction numbers with like denominators.

Example: $3 \dfrac{1}{8}$ by $2 \dfrac{3}{8}$

Ans: $3 \dfrac{1}{8} \div 2 \dfrac{3}{8}$

Convert the mixed fraction to improper faction i.e.,

$3 \dfrac{1}{8}=\dfrac{25}{8}$ and $2 \dfrac{3}{8}=\dfrac{19}{8}$

We will multiply the reciprocal of the second fraction with the first fraction

$\dfrac{25}{8} \times \dfrac{8}{19}$

The numerators and denominators of these fractions are multiplied separately

$\dfrac{25 \times 8}{8 \times 19}$

If there are common divisors in the numerator and denominator, cancel them out. Here we remove 8.

Now we get $\dfrac{25}{19}$

Now convert it to the mixed fraction i.e, $\dfrac{25}{19}=1 \dfrac{6}{19}$

Dividing Mixed Fractions with Unlike Denominators

Dividing mixed numbers with different denominators is defined as dividing mixed numbers with different denominators. The steps to perform splitting are the same as described in the previous section. Let's look at an example to understand the division of mixed numbers with unequal denominators.

Example : $2 \dfrac{2}{9}$ by $3 \dfrac{1}{7}$

Ans: Convert the mixed fraction to improper faction i.e, $2 \dfrac{2}{9}=\dfrac{20}{9}$ and $3 \dfrac{1}{7}=\dfrac{22}{7}$

We will now divide $\dfrac{20}{9}$ by $\dfrac{22}{7}$

$\dfrac{20}{9} \div \dfrac{22}{7}$

$\dfrac{20}{9} \times \dfrac{7}{22}$

$\dfrac{10 \times 7}{9 \times 11}$ (by cancelling 2 from the numerator and denominator)

$\dfrac{70}{99}$

Dividing Mixed Fractions by Whole Numbers

Integer can be written in fractions with denominators of 1. For example, 9 can be written as $\dfrac{9}{1}$. To divide a mixed number by an integer, convert the mixed number to an improper fraction, represent the integer as a fraction, and then perform the procedure for dividing a mixed number as described in the previous section. To understand, go through the example below.

Example 1: $4 \dfrac{1}{5}$ by 7

Ans. $4 \dfrac{1}{5} \div 7$

Now convert $4 \dfrac{1}{5}$ to improper function $\dfrac{21}{5}$ and the whole number 7 can be written as $\dfrac{7}{1}$

We will now divide $\dfrac{21}{5}$ by $\dfrac{7}{1}$

$=\dfrac{21}{5} \div \dfrac{7}{1}$

$=\dfrac{21}{5} \times \dfrac{1}{7}$

$=\dfrac{21 \times 1}{5 \times 7} \text { (Here we cancelled out } 21 \text { from the } 7)$

$=\dfrac{3}{5}$

Dividing Mixed Fractions with Fractions

Dividing a mixed number by a fraction is the division between a mixed number and a proper fraction. The steps to share them are the same as explained before. Convert the mixed fraction to an improper fraction and divide by the given fraction according to the division procedure. To understand, go through the example below.

Example $2: 5 \dfrac{2}{3}$ by the fraction $\dfrac{2}{9}$

Ans. We will convert the mixed fraction into improper fraction $\dfrac{17}{3}$

$\dfrac{17}{3} \div \dfrac{2}{9}$

$\dfrac{17}{3} \times \dfrac{9}{2}$

$\dfrac{17 \times 9}{3 \times 2} \text { (Here we cancelled out } 9 \text { by } 3 \text { ) }$

$\dfrac{17 \times 9}{2}=\dfrac{51}{2}=25 \dfrac{1}{2}$

Practice Questions

Q1. $\dfrac{3}{15} \div 2 \dfrac{6}{15}$

Ans. $\dfrac{1}{4}$

Q2. $\dfrac{2}{5} \div 3 \dfrac{4}{7}$

Ans. $\dfrac{14}{125}$

Q3. $6 \dfrac{1}{2} \div 2 \dfrac{1}{4}$

Ans. $\dfrac{26}{9}$

Q4. $8 \dfrac{2}{5} \div 4 \dfrac{2}{7}$

Ans. $1 \dfrac{24}{25}$

Summary

In this article, we learned that a mixed fraction consists of a whole number with a proper fraction. We also learned how to divide mixed fractions when both fractions have the same and different denominators. We also learned how to divide mixed fractions with whole numbers with the help of examples and when mixed fractions with the Improper fraction with the help of examples. There are some practice questions related to examples. Practice them then you will easily solve the mixed fractions division.