Distance from origin formula in 2D and 3D with solved examples
Here, you will discover how to use the distance formula to determine the separation between two points on a plane. Distance is the length that separates any two points on a line. We fix the locations of the points on the plane and their separation since we are aware of the coordinates of the two points on the plane. There is an algebraic relationship between two points' distance and coordinates.
Distance
The length of the line connecting two places is used to measure the distance between them. The distance between two points that are on the same horizontal or vertical axis can be calculated by deducting the mismatched coordinates.
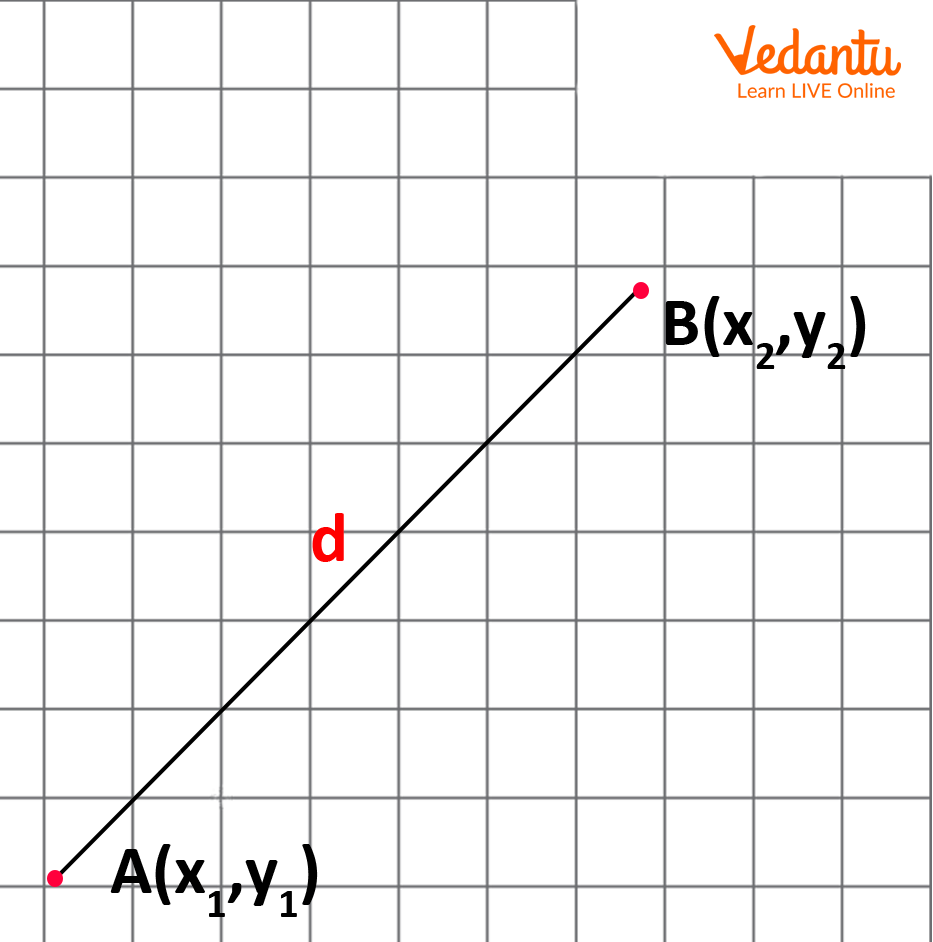
Distance
Origin
The origin is the intersection of the system axes. The origin divides each of these axes into two halves, the positive semi-axis, and the negative semi-axis. All coordinates of the origin are equal to zero that is [0,0].
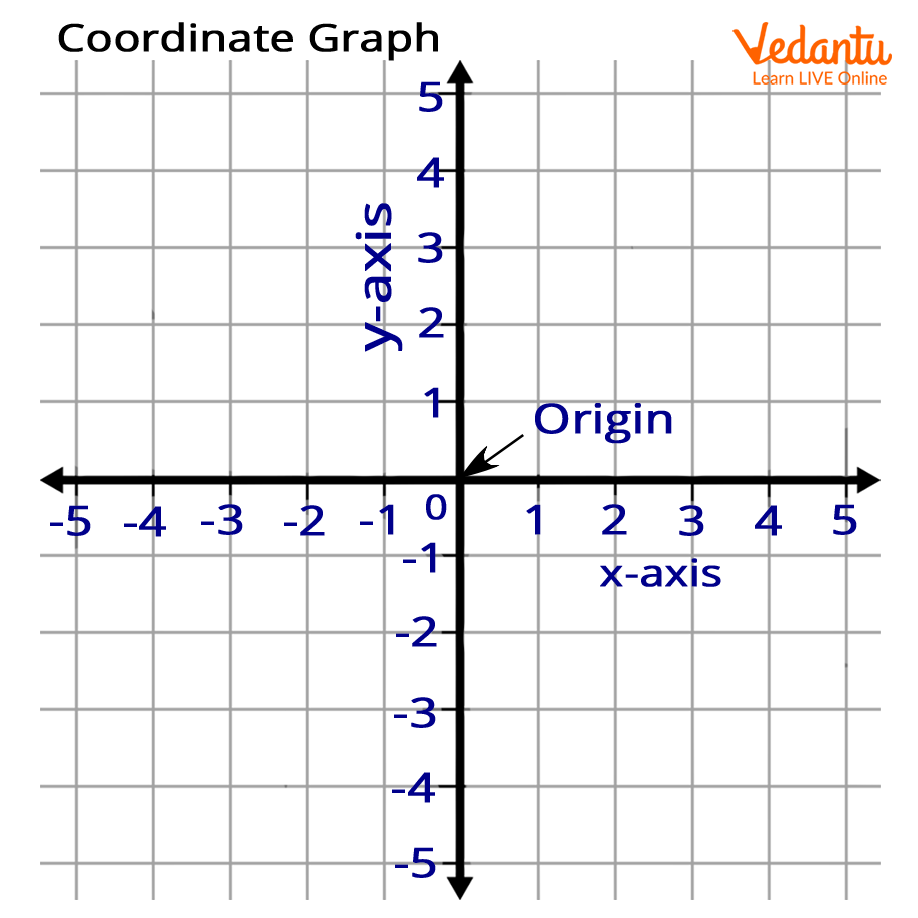
Origin
One Dimensions
The bare minimum of coordinates required to identify a location in the mathematical space is known as a dimension in geometry. A one-dimensional (1D) object is one for which a point on the object may be defined using just one coordinate, according to this description.
A common definition of a 1D object is one with a length but no breadth, depth, or thickness. Lines, rays, and line segments are a few examples of geometric objects that fulfil this criterion. Rays have a single endpoint and an indefinitely long other end, while line segments have two endpoints. In the given image the two end points \[A = {x_1}\] and \[B = {x_2}\] are the two endpoints.
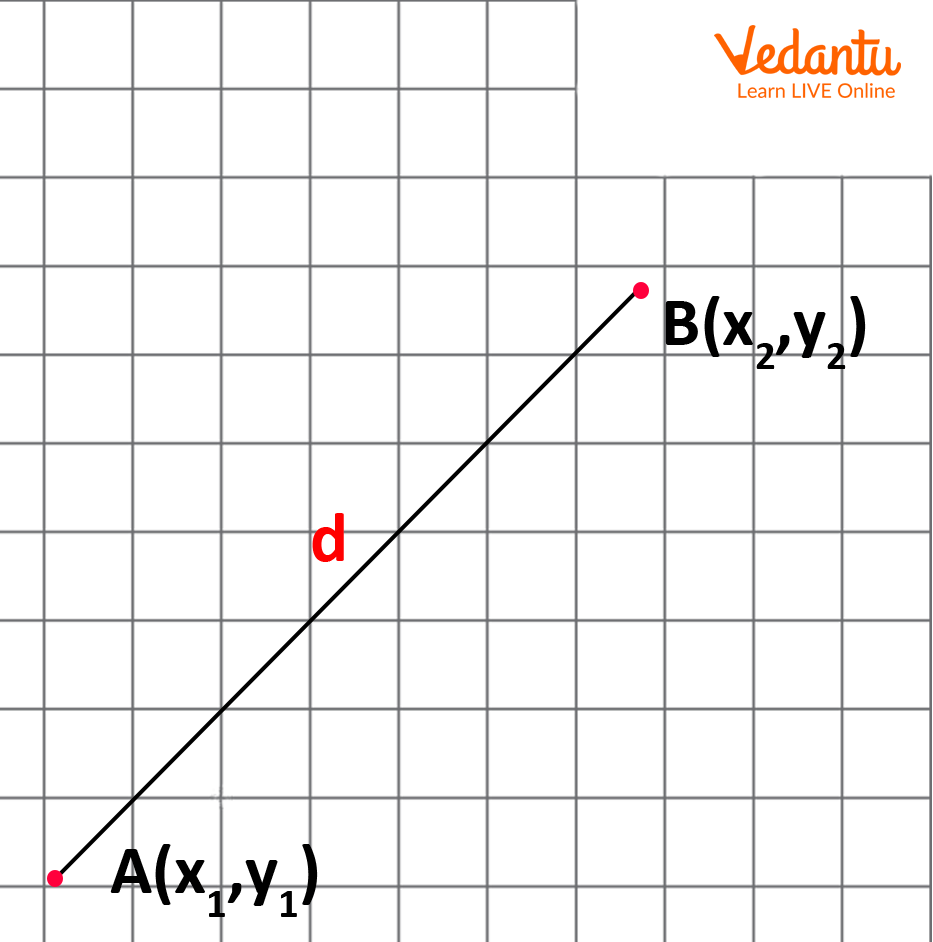
One Dimensions
Formula to Find Distance Between Two Points of One Dimensions
Suppose \[A = {x_1}\] and \[B = {x_2}\] are two points lying on the real number line. Then the distance between A and B is
\[d(A,B) = \mid {{\bf{x}}_1} - {{\bf{x}}_2}\mid \]
The distance between any two locations on the x-axis may be calculated as the absolute value of the difference between their x-coordinates because we can think of the x-axis in the plane as a one-dimensional number line. Similar to this, the absolute value of the difference in the y-coordinates of any two locations on the y-axis is the distance between them.
Now, consider the xy-plane, and suppose \[{P_1} = ({x_1},{y_1})\] and \[{P_2} = ({x_2},{y_2})\] are two points in it . Then the distance between \[{P_1}\] and \[{P_2}\] is
\[d({P_1},{P_2}) = \sqrt {{{({x_1} + {x_2})}^2} + {{({y_1} + {y_2})}^2}} \]
Solved Examples
1. Find the distance between the points (2,4) and (4,5)
Solution: Using distance formula between the two points.
\[{\rm{d}} = \sqrt {{{[{\rm{y}}2 - {\rm{y}}1]}^2} + {{[{\rm{x}}2 - {\rm{x}}1]}^2}} \] \[{\rm{d}} = \sqrt {{{[5 - 4]}^2} + {{[4 - 2]}^2}} \]
\[{\rm{d}} = \sqrt {{{[1]}^2} + {{[2]}^2}} \]
\[{\rm{d}} = \sqrt {[1 + 4]} \]
\[{\rm{d}} = \sqrt 5 \]units
Therefore the distance between the given points is \[\sqrt 5 \]units
2. Find the distance of a point (0,5) from origin.
Solution: Let \[[{\rm{x}}1,{\rm{y}}1]\] \[ = [0,5]\] and \[[{\rm{x2}},{\rm{y2}}]\] \[ = [0,0]\]
Now, Using distance formula between the two points:
\[{\rm{d}} = \sqrt {{{[0 - 5]}^2} + {{[0 - 0]}^2}} \]
\[{\rm{d}} = \sqrt {{{[ - 5]}^2} + {{[0]}^2}} \]
\[{\rm{d}} = \sqrt {25 + 0} \]
\[d = \sqrt {[25]} \]
\[{\rm{d}} = 5\]units
Therefore the distance between the given points is 5 units.
3. Find points on the y-axis that are equidistant from points (-1, 2) and (2, 3).
Solution: It is known that the x-coordinate of any point on the y-axis is zero.
So assume that the point equidistant from these points is (0, k). that,
According to the given condition:
Distance between (0, k) and (-1, 2) = Distance between [0, k] and [2, 3]
\[\sqrt {{{[ - 1 - 0]}^2} + {{[2 - k]}^2}} = \] \[\sqrt {{{[2 - 0]}^2} + {{[3 - k]}^2}} \]
Squaring both sides
\[{[ - 1 - 0]^2} + {[2 + k]^2} = {[2 - 0]^2} + {[3 - k]^2}\]
\[1 + 4 + {k^2} + 4k = 4 + 9 + {k^2} + 6k\]
\[2{\rm{k}} = 8\]
\[{\rm{k}} = 4\]
So the desired point \[[0,{\rm{k]}} = [0,4]\]
Summary
We now know that the Origin is the place where the axes converge. For each variable, the coordinates at the origin are zero. Next, we discovered how to get the formula for calculating the distance between two places. By putting your knowledge and comprehension of this subject to use and by working through worksheets on it, you may apply and improve both. The one-dimensional line contains two points at its beginning and finish, and we can use those points to calculate their distance from one another.
FAQs on Distance From Origin in Coordinate Geometry
1. What is the distance from origin in coordinate geometry?
The distance from origin is the straight-line distance between a point and the origin (0, 0) in the Cartesian plane. In coordinate geometry, the origin is the point where the x-axis and y-axis intersect. The distance measures how far a point (x, y) is from (0, 0) using the distance formula derived from the Pythagorean theorem.
2. What is the formula for distance from origin?
The formula for the distance from origin of a point (x, y) is d = √(x² + y²). This formula comes from the Pythagorean theorem, where:
- x is the horizontal distance from the y-axis
- y is the vertical distance from the x-axis
- d is the straight-line distance from (0, 0)
3. How do you find the distance from origin of a point?
To find the distance from origin, substitute the coordinates into d = √(x² + y²) and simplify. Follow these steps:
- Square the x-coordinate
- Square the y-coordinate
- Add the two squares
- Take the square root of the result
4. Why is the distance from origin formula √(x² + y²)?
The formula √(x² + y²) is used because it is derived from the Pythagorean theorem. A point (x, y) forms a right triangle with the x-axis and y-axis, where:
- One leg = x
- Other leg = y
- Hypotenuse = distance from origin
5. Can the distance from origin be negative?
No, the distance from origin can never be negative because distance is always a non-negative quantity. Since the formula is d = √(x² + y²), both x² and y² are non-negative, and the square root of a non-negative number is also non-negative. Therefore, distance is always zero or positive.
6. What is the distance from origin of the point (−5, 12)?
The distance from origin of (−5, 12) is 13. Using the formula:
- d = √(x² + y²)
- d = √((−5)² + 12²)
- d = √(25 + 144)
- d = √169 = 13
7. How is the distance from origin related to the distance formula?
The distance from origin formula is a special case of the general distance formula between two points. The general formula is:
- d = √[(x₂ − x₁)² + (y₂ − y₁)²]
- d = √[(x − 0)² + (y − 0)²]
- d = √(x² + y²)
8. What is the distance from origin in three dimensions?
In three dimensions, the distance from origin of a point (x, y, z) is d = √(x² + y² + z²). This formula extends the Pythagorean theorem to 3D space. For example, for (2, 3, 6):
- d = √(2² + 3² + 6²)
- d = √(4 + 9 + 36)
- d = √49 = 7
9. What does it mean if a point is equidistant from the origin?
If a point is equidistant from the origin, it means its distance from (0, 0) is the same as another point’s distance. All points satisfying x² + y² = r² lie at the same distance r from the origin. These points form a circle centered at the origin with radius r.
10. What are common mistakes when finding distance from origin?
Common mistakes when calculating distance from origin include incorrect squaring and sign errors. Key things to remember:
- Always use d = √(x² + y²)
- Square both positive and negative values correctly
- Do not forget the square root at the end
- Distance cannot be negative
