




Quick Steps to Change Fractions into Decimals
Before learning decimal fractions, one must understand normal fractions. There are two parts of a fraction: a numerator and a denominator. It is best to write fractions as follows:
$\frac{x}{y}$
In this example, X represents the numerator, and Y represents the denominator. A fraction with a decimal denominator (y in the image) is one in which the numerator is 10, or the numerator can be a multiple of 10, such as 100, 1000, 10000, etc. Numerators can range from -infinity to +infinity. Fractions with decimal points are called decimal numbers.
In mathematics, decimal fractions are numbers whose denominator is ten, or powers of ten, such as 101, 102, or 103.
Decimal Fraction Examples
0.0007 is the decimal form of \[ \frac{7}{10000} \] which is a decimal fraction.
The decimal fraction 1.9 is \[ \frac{19}{10,} \] a decimal fraction.
The decimal fraction 0.039 represents the fraction \[ \frac{39}{1000.} \]
In addition to decimal fractions, there are fractions with non-ten numbers in the denominator.
For Example,
\[ \frac{37}{8} \]
\[ \frac{2}{1083} \]
\[ \frac{83}{145} \]
Fractions Read as Decimals
In the case of 1 in the numerator, let us consider the following scenario. The concept of the numerator will be explained by considering different denominators.
\[ \frac{1}{10} \] is read as one-tenth.
\[ \frac{1}{100} \] is read as one-hundredth.
\[ \frac{1}{1000} \] is read as one-thousandth.
When the value of the numerator is greater than one, we add an ‘s’ to the name. So, for the case, 3/10 is read as three-tenths.
A Decimal Riddle
Operative Sahmaj is on a hunt to find some stolen treasure. His indication is a combination of a locked room inside an abandoned storehouse. Operative Sahmaj reaches the door and gets ready to enter the combination into the cinch, but to his surprise, the cinch can only be opened using figures in decimal form. But the Operative's indication is made of fragments! How will he break this riddle? Let’s read ahead!

Parts of The Whole
Corridor of a Whole
Fragments and numbers are both ways to represent the corridor of a whole - both a bit and a decimal expresses a number that's lower than one. Operative Sahmaj needs to convert his fragments into numbers. Occasionally, in order to complete a calculation problem, you'll also need to convert a bit into a numeric. Let's look at the process and break Operative Sahmaj's riddle.
Meanings of Fragments and Numbers
When you read a decimal number, which is a way of expressing a number lower than one with the use of a period, it's easy to see the relationship between numbers and fragments. The decimal number 0.5 is read as 'five-tenths.' That's the same way you would read this bit \[ \frac{5}{10.} \] The only thing that makes it a bit different from a numeric is that it expresses a number lower than one with gusto or a rent symbol. So, a numeric can be written as a bit using its place value.
Look at these exemplifications:
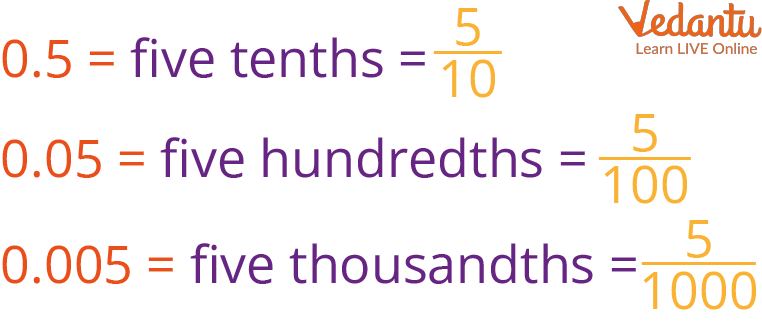
Decimal to Fraction
As you can see, we've our 0.5 to \[ \frac{5}{10} \] illustration, but we also have 0.05 equaling five one-hundredths and 0.005 equaling five one-thousandths. It just goes up from there grounded on the number of bottoms. It's really as simple as that. But, how do we get these numbers to turn into fragments?
Converting Fragments into Decimals
Now that we understand the meaning of numbers, it's time to change fragments into numbers. The line is a bit that separates the numerator from the denominator means ''divided by.'' The bit 2/5 can be read as two-fifths, or it can be read as two divided by five. To turn a bit into a numeric, we divide the numerator by the denominator.
Let's convert the first bit, \[ \frac{2}{5,} \] into a numeric. We'll review the way of long division while we break this problem. Let's look at this division problem.
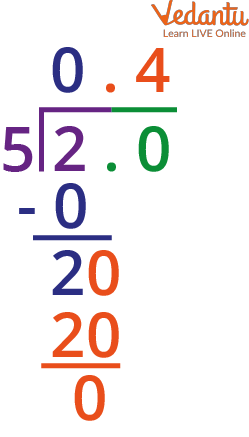
Decimal Division
Solved Examples
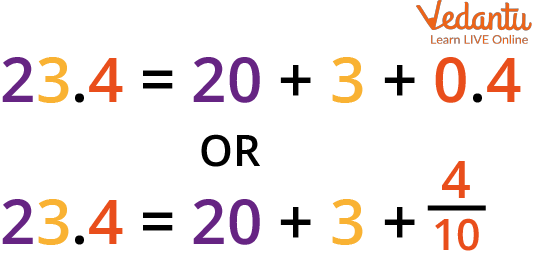
Example of Decimal Number

Example 2
Practice Question
1. Convert fraction to decimal.
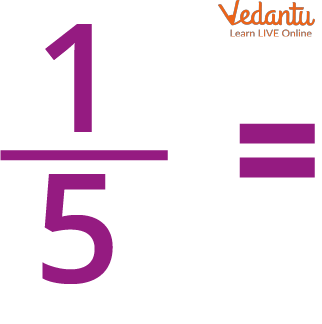
Fraction (1/5)
Ans: 0.2
2. Convert fraction to decimal.
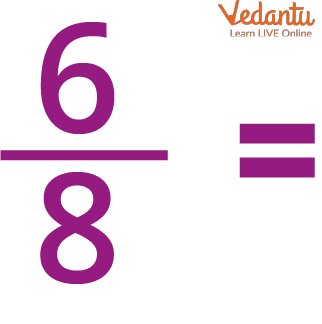
Fraction (6/8)
Ans: 0.75
Summary
Decimal fragments encourage scholars to learn about precise amounts. Weights such as 3.2 kg and distances such as 7.85 km will be easier for them to understand. The first step towards a better understanding of decimal figures is rehearsing decimal bit problems every day. The idea of taking a pen and paper to break totalities is dull and uninteresting for scholars. They need amusing ways to allure them towards exercising their totalities.
FAQs on Fraction to Decimal Conversion Made Simple
1. What is a decimal bit illustration and what is a decimal bit in the simplest form?
A decimal bit is a bit with a power of 10 (101, 102, etc.) in the denominator. These figures are written in decimal form for the convenience of working fine totalities. For illustration, \[ \frac{4}{1000} \] is a decimal bit, written in numbers as 0.004.
The simplest form of a decimal bit is the introductory in-separable bit obtained by dividing the numerator by the denominator. For illustration, the simplest form of the decimal bit \[ \frac{4}{10} \] is \[ \frac{2}{5.} \]
2. Where are decimal fragments used? Convert the decimal 0.25 into a reduced bit form.
Decimal fragments are used for expressing the weight of people and products. It can also be used to determine abatements in the price of products and measure the constituents of a form. The numeric, 0.25, has two decimal places. Hence, its bit form will be attained by taking the numeric without the decimal point and dividing it by the alternate power of 10.
Therefore, we get 0.25 = \[ \frac{25}{102} \] = \[ \frac{25}{100.} \]
Now, we can reduce the bit \[ \frac{25}{100} \] by dividing the numerator and denominator both by 5 to get \[ \frac{25}{100} \] = \[ \frac{5}{20.} \] Also, we divide the numerator and denominator both by 5 again to gain \[ \frac{5}{20} \] = \[ \frac{1}{4.} \]
3. Why do we convert fractions to decimals?
It is a way to represent a fraction by a set of common denominators: \[\frac{1}{10,} \frac{1}{100} \] ... The advantage of decimals is that because all of them are in common denominators already, addition, subtraction, and comparison are quite straightforward.

















