




Step-by-Step Guide: Calculate Area with Sides and Diagonal
In this article, we will learn about the general formula for the area of a quadrilateral with a diagonal calculator with the help of many solved examples. As we know that the area of a quadrilateral is the region enclosed by the sides of the quadrilateral. We are already acquainted with the term area.
It is defined as the region that is occupied inside the boundary of an object or figure. Its measurement is done in square units and the standard unit being square meters $\left(\mathrm{m}^2\right)$. Since we know that a polygon with four sides is called a quadrilateral. Hence, we shall learn about finding the area of a quadrilateral with sides and diagonals. A quadrilateral can be a square, rectangle, rhombus, parallelogram or trapezium.
Properties of Quadrilateral
Each of the quadrilaterals discussed above has its properties.
Though, some properties are common to all quadrilaterals.
They are as follows.
They have four sides.
They have four vertices.
They have two diagonals.
The sum of all interior angles is $360^{\circ}$.
Area of Quadrilateral with Diagonal
The formula for the area of the quadrilateral can be found using different methods like dividing the quadrilateral into two triangles, using Heron’s formula or using the sides of the quadrilateral. So now let us discuss all methods in detail.
Area of Quadrilateral by Dividing it into Two Triangles
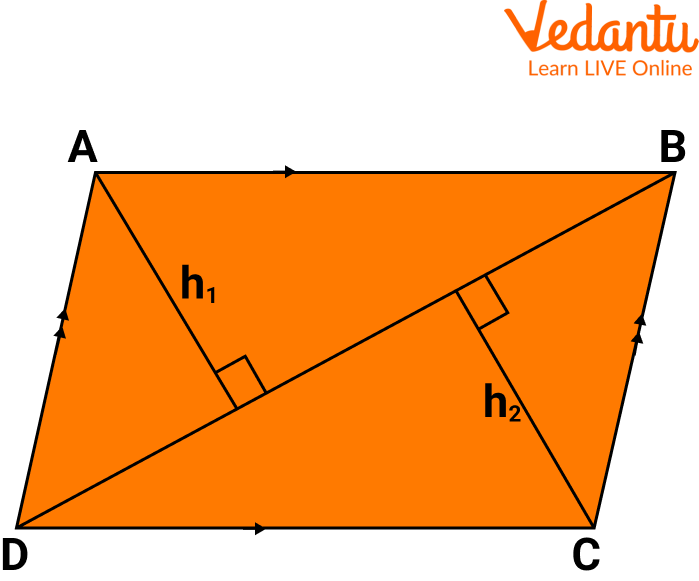
Consider a quadrilateral PQRS of different lengths; now, let us derive a formula for the area of a quadrilateral.
We can see the quadrilateral as a combination of two triangles, with the diagonal PR being the common base.
$h_{1}$ is the height of PSR and $h_{2}$ is the height of PQR, respectively.

Area of the Quadrilateral with Diagonal
The area of quad PQRS is equal to the sum of the area of triangle PSR and the area of triangle PQR.
Area of triangle PSR $=\frac{(\text { base } \times h e I g h t)}{2}=\frac{\left(P R \times h_1\right)}{2}$ Area of triangle $P Q R=\frac{(\text { base } \times \text { height })}{2}=\frac{\left(P R \times h_2\right)}{2}$
Thus, the area of quadrilateral $P Q R S$ is equal to the Area of triangle $\mathrm{PSR}+$ Area of triangle $\mathrm{PQR}=\frac{P R \times h_1}{2}+\frac{P R \times h_2}{2}=P R\left(\frac{h_1+h_2}{2}\right)$ $=\frac{1}{2} P R \times\left(h_1+h_2\right)$
Hence the area of a general quadrilateral formula is, $=\frac{1}{2} \times$ diagonal $\times($ the sum of the height of two triangles $)$
Area of Quadrilateral with Diagonal Formula
Following are the area of quadrilateral with diagonal:
Solved Questions
Some solved examples based on the area of the quadrilateral with a diagonal calculator are given below:
Q 1. In the quadrilateral, ABCD is shown below, the side BD = 15 cm. The heights of the triangles ABD are 5cm and BCD 7 cm, respectively. Find its area.
Quadrilateral
Ans:
Diagonal $=\mathrm{BD}=15 \mathrm{~cm}$
Given Heights, $h_1=5 \mathrm{~cm}$ and $h_2=7 \mathrm{~cm}$
Sum of the heights of the triangles $=h_1+h_2=5+7=12 \mathrm{~cm}$
Thus, the area of quadrilateral $A B C D$ is:
$A=12 \times$ diagonal $\times$ (Sum of the height of two triangles)
$=\frac{(15 \times 12)}{2}=90 \mathrm{~cm}^2$
Thus the area of the quadrilateral is $90 \mathrm{~cm}^2$.
Q 2. Find the sides and area of a square when the diagonal is given as $6 \mathrm{~cm}$.
Ans: Let us take a square of side $x$. If the square is divided into two right-angled triangles, then the hypotenuse of each triangle is equal to the diagonal of the square. As given, the diagonal is equal to $6 \mathrm{~cm}$.
According to Pythagoras's theorem,
$x^2+x^2=6^2$
$2 x^2=36$
$x^2=18$
$x=\sqrt{18}$
$x=3 \sqrt{2}$ units
To find the area of a square when a diagonal is given, we can use any of the below methods:
$\text { Area of a square }=\text { side } \times \text { side }=3 \sqrt{2} \times 3 \sqrt{2}$
$=9 \times 2=18 \mathrm{~cm}^2$
Practice Questions
Q1. Calculate the area of a quadrilateral with the given measurements:
Perpendicular heights = 60 m and 20 m, Diagonal = 50 m
Solution: Area $=2000 \mathrm{~m}^2$
Q2. A quadrilateral has four equal sides each of length $4 \mathrm{~cm}$. Find its area?
Solution. Area $=16 \mathrm{~m}^2$
Q3. The length of a quadrilateral (rectangle) is $6 \mathrm{~m}$ and the breadth is $5 \mathrm{~m}$. Find the area of the rectangle.
Solution: Area $=30 \mathrm{~m}^2$
Summary
In this article, we have discussed the area of quadrilaterals with a diagonal formula for different types of quadrilaterals. These formulas help you to calculate the area of a rectangle, square, parallelogram, rhombus, and trapezium. We have also discussed the area of the quadrilateral with a diagonal calculator. A quadrilateral can also be divided into two triangles, calculating the area of each triangle given its vertices, and then adding these values to get the required total area of the quadrilateral with sides and diagonals.
FAQs on Area of Quadrilateral Using Diagonal: Explained with Examples
1. What is the main formula for finding the area of a quadrilateral when one diagonal and its corresponding heights are known?
The primary formula to calculate the area of a general quadrilateral is: Area = ½ × d × (h₁ + h₂). In this formula, 'd' represents the length of the diagonal, and 'h₁' and 'h₂' are the lengths of the perpendiculars (heights) drawn from the remaining two vertices to that diagonal.
2. How do you find the area of an irregular quadrilateral with four unequal sides?
To find the area of an irregular quadrilateral, you can divide it into two triangles by drawing one of its diagonals. The area of the quadrilateral is the sum of the areas of these two triangles. If you know the length of the diagonal and the heights from the other vertices to it, you can use the formula A = ½ × d × (h₁ + h₂). If you know the lengths of all four sides and the diagonal, you can use Heron's formula for each triangle.
3. Why is dividing a quadrilateral into two triangles a standard method for calculating its area?
This method is used because triangles are fundamental shapes with simple, well-defined area formulas (e.g., ½ × base × height). By decomposing a more complex shape like a quadrilateral into two triangles, we can use these reliable formulas to find the area accurately. The chosen diagonal acts as a common base for both triangles, which simplifies the overall calculation.
4. Can you provide an example of how to calculate the area of a quadrilateral using its diagonal?
Certainly. Imagine a quadrilateral with a diagonal of length 20 cm. The heights of the perpendiculars from the other two vertices to this diagonal are 8 cm and 6 cm. Using the formula:
Area = ½ × d × (h₁ + h₂)
Area = ½ × 20 × (8 + 6)
Area = 10 × 14
Area = 140 cm².
5. Is it possible to find the area of a quadrilateral if only the lengths of its four sides and one diagonal are given?
Yes, this is a very practical application. When the lengths of all four sides and one diagonal are known, the quadrilateral is divided into two triangles whose side lengths are all known. You can then apply Heron's formula individually to each triangle to find its area. The total area of the quadrilateral is the sum of the areas of these two triangles.
6. How is the formula A = ½ × d × (h₁ + h₂) for the area of a quadrilateral derived?
The formula is derived directly from the area of a triangle. When you draw a diagonal 'd' in a quadrilateral, you create two triangles.
- The area of the first triangle is ½ × base × height = ½ × d × h₁.
- The area of the second triangle is ½ × base × height = ½ × d × h₂.
7. Does the choice of diagonal affect the final calculated area of a quadrilateral?
No, the choice of which diagonal to use for the calculation does not affect the final area. A quadrilateral has two diagonals, and either one can be used to split it into two triangles. As long as you use the correct corresponding heights for the chosen diagonal, the total calculated area will remain the same, as it is a fixed property of the shape.
8. What are the standard units used to express the area of a quadrilateral?
The area of a quadrilateral, like any two-dimensional shape, is expressed in square units. The specific unit depends on the unit of length used for its sides and diagonals. Common examples include square metres (m²), square centimetres (cm²), and square inches (in²).

















