Triangle Area and Perimeter

The length of a triangle's three sides together equals its perimeter. The region or surface enclosed by a triangle's form is known as the triangle's area. When we fence the backyard garden or hang Christmas lights around the home, we discover the Perimeter. Similarly, we determine the size of the carpet purchased by measuring the area of the room's floor. We will learn here how to find the area from the perimeter. This article will consider all the points related to the area and perimeter of the triangle. This is going to help you a lot.

What is a Triangle?

Let's remember some key concepts to find triangle area and perimeter:

• A triangle is a polygon with three sides.

• The vertices are the three points where two sides (the corners) meet.

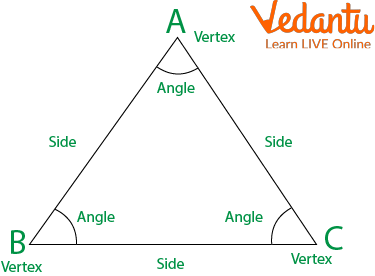
A Triangle

• The height is the perpendicular line segment that joins a side with the vertex opposite that side.

• Since there are three sides, there are three heights. The three heights intersect at a single point called the orthocentre.

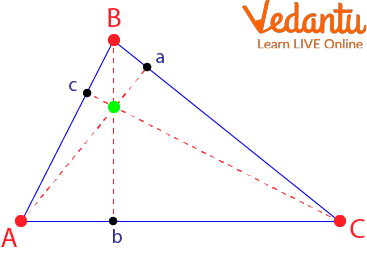
Orthocentre Triangle

• The base of a triangle, b, is any of its three sides (usually, the lower side parallel to the horizontal axis is chosen). Once the base is chosen, we will call the height of the triangle h, i.e. the height perpendicular to the base.

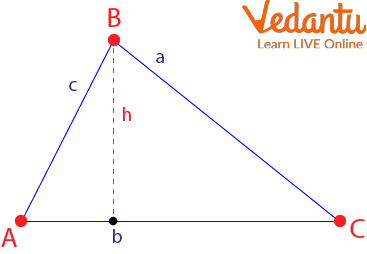
Triangle ABC

Now let’s learn about the area and perimeter of the triangle formula.

The Perimeter of a Triangle

The lengths of a triangle's three sides add up to its perimeter. If the sides of the triangle measure $a, b$, and $c$, then its perimeter is

$P=a+b+c$

Here, P is the perimeter of a triangle.

The semi-perimeter of a triangle is half its perimeter:

$s=\dfrac{a+b+c}{2}$

Calculate the Perimeter of an Isosceles Triangle

On the other hand, isosceles triangles are those in which two of their sides are equal, and one is different, which will be the base. So, in this case, to find the perimeter of the triangle, you must apply the formula that says that you must multiply the value of the side by two and add the length of the base: $P=2 l+b$

The Perimeter of a Right Triangle

The perimeter of a right triangle is the sum of the three sides.

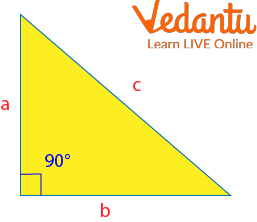
Right-angled Triangle

Thus, $P=a+b+c$

If the two legs ( $a$ and $b$ ) are known, their perimeter can be calculated from them.

This is because, thanks to the Pythagorean theorem, the hypotenuse $(c$ can be expressed as a function of the legs ( $a$ and $b$ ).

$P=a+b+\sqrt{a^2+b^2}$

Area of a Triangle

We have several ways to calculate the area of ​​a triangle: from the base and height or from its sides and semi-perimeter.

The area of ​​a triangle is half the product of its base times its height:

$A=\dfrac{b \times h}{2}$

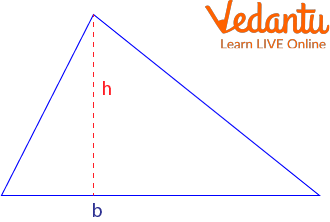
A Triangle with Base b

Also, we can calculate the area from its sides $a, b, c$ and its semi-perimeter $s$ using the following formula, called Heron's formula:

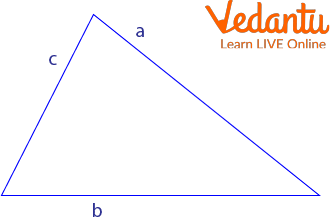
Triangle with Sides a,b,c

$A=\sqrt{s(s-a)(s-b)(s-c)}$

$s=\dfrac{a+b+c}{2}$

Some triangle area and perimeter examples are given below.

Solved Examples

Example 1: Find the perimeter and semi-perimeter of a triangle with sides 3cm, 4cm, and 5cm.

Ans: The perimeter of the right triangle is given by

$P=3+4+5$

$P=12$cm

And its semi-perimeter is given by

$s=\dfrac{3+4+5}{2}$

$s=\dfrac{12}{2}$

$s=6$cm

Example 2: Find the area of ​​the right triangle with sides 3cm, 4cm, and 5cm.

Ans:

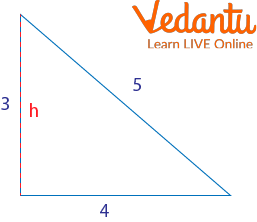
The Triangle Formed

$A=\dfrac{b \times h}{2}$

$A=\dfrac{4 \times 3}{2}$

$A=\dfrac{12}{2}$

$A=6\, \mathrm{cm}^2$

Example 3: Find the area of the right triangle with sides 3cm, 4cm, and 5cm using heron's formula.

Ans: We saw in an example that the semi-perimeter of the right triangle with sides 3cm, 4cm, and 5cm is 6cm

We calculate its area from Heron's formula:

$A=\sqrt{s(s-a)(s-b)(s-c)}$

$A=\sqrt{6(6-3)(6-4)(6-5)}$

$A=\sqrt{6 \times 3 \times 2 \times 1}$

$A=\sqrt{36}$

$A=6 \mathrm{cm}^2$

So, Area is $6 \mathrm{cm}^2$

Practice Questions

Q 1: Calculate the area of the equilateral triangle with side $4 m$.

Ans: $A=6928 m^2$

Q 2: Find the Area of a right-angled triangle whose lengths of the sides other than the hypotenuse are $12 \mathrm{~cm}$ and $5 \mathrm{~cm}$.

Ans: ${30 \mathrm{~cm}^2}$

Summary

In this article, we, first of all, learned about the triangle. Then we learned about the area and perimeter of a triangle formula. i.e. The area of a triangle is given by $A=\dfrac{b \times h}{2}$. Similarly, the perimeter of the triangle is given by $P=a+b+c$. We have also seen Heron's formula to find the area and the perimeter. i.e. $A=\sqrt{s(s-a)(s-b)(s-c)}$ and semi - perimeter $s=\dfrac{a+b+c}{2}$. In the end, we have added some solved examples and practice problems so that you will get the proper command of the topic.