What Is the Angle Symbol in Geometry and How to Use It
You must have heard your elders say, “90 degrees angle” or “45 degrees angle” and every time you asked them what is the meaning of it, they must have told you, “You won’t understand. You are a kid”. Don’t worry! We are here to help you to be a smart kid. Let’s learn about angles and the angle symbol. Also, we have a fun activity and a quiz for you to make sure that next time an elder talks about angles, you know it already.
Let’s Define an Angle
When two straight lines or rays meet at a common end-point, the shape formed is called an angle in geometry. The symbol ∠ shows what an angle looks like. Usually, angles are also represented by alphabets, such as ∠AOB or ∠ABC. Note that the middle alphabet, i.e., O in ∠AOB and B in ∠ABC are the common end points where the two lines meet to form the angle symbol.
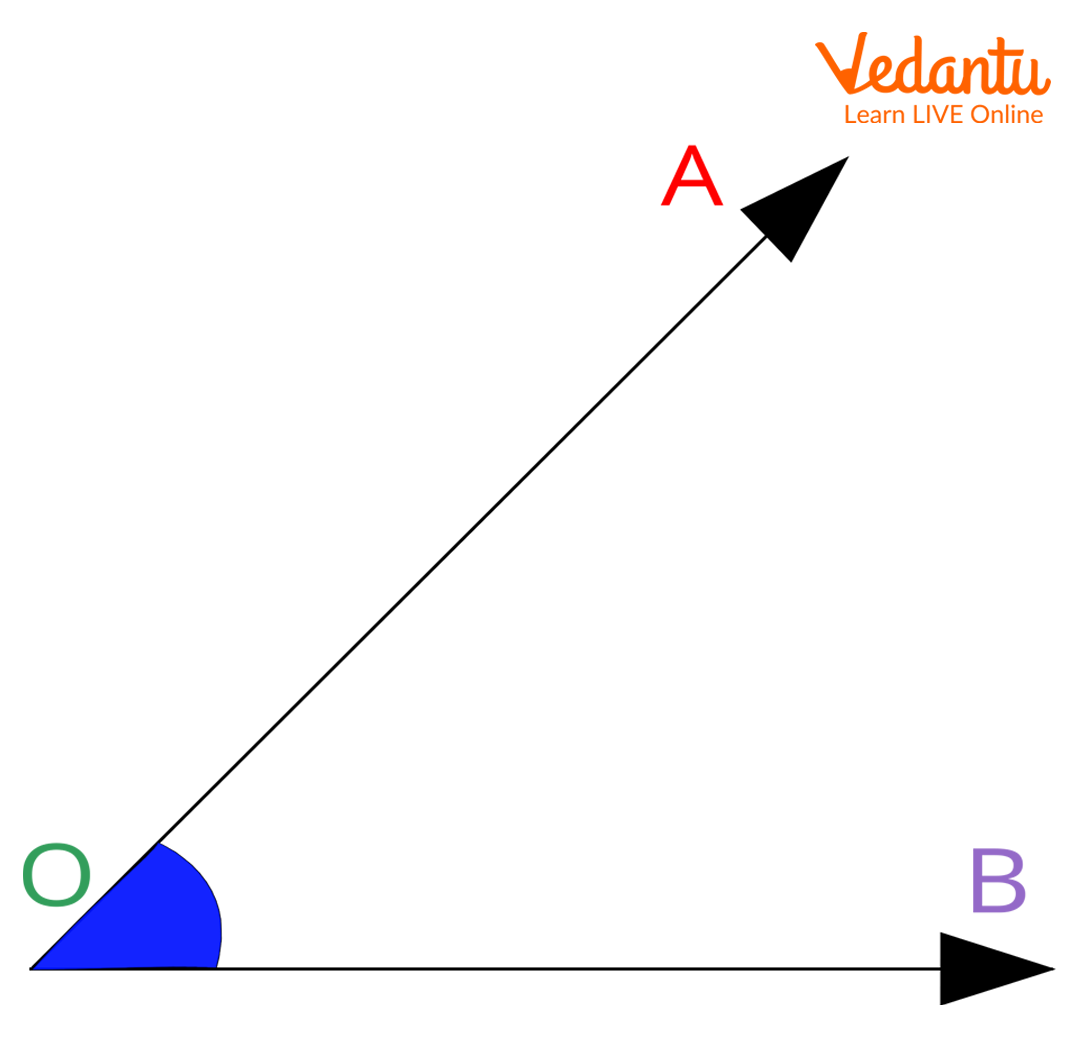
Image: Angle AOB
Parts of an Angle
Now that you know what an angle is. Let’s learn about the parts of an angle.
Arms: The arms of an angle are also known as its sides. The two lines or rays that come together to form an angle are the arms or sides of an angle. For instance, in the image given below, side AB and side BC are the arms of ∠ABC.
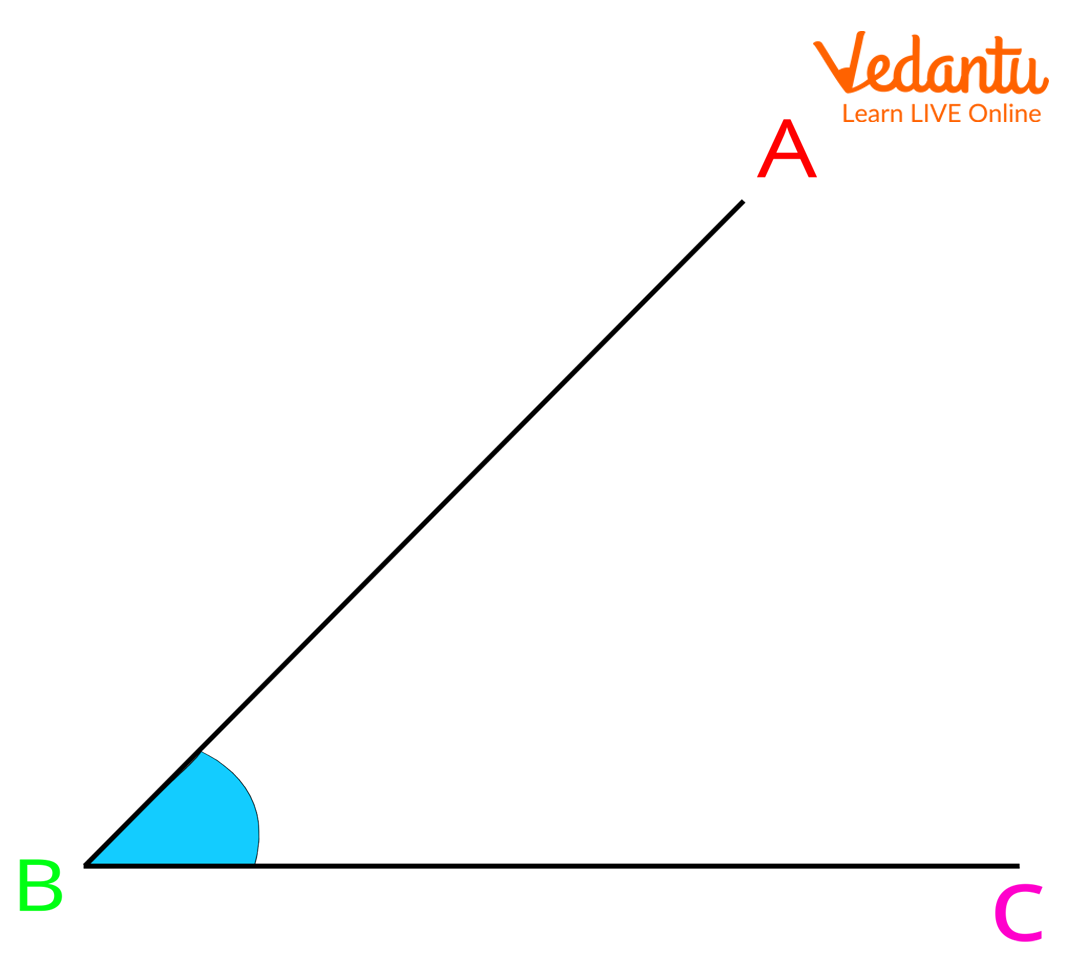
Vertex: In ∠ABC given above, side AB and BC have a common end point, which is point B. It is the point where the two arms of angle ABC meet. This point is called the vertex (plural: vertices) of an angle. Here, point B is the vertex of angle ABC.
How to Measure an Angle?
Ask your brother or sister to show you a protractor from their geometry box. A protractor is an instrument used to measure an angle. Like all other objects angles too have units of measure. We are going to discuss the two main units that are used to measure the size of an angle, i.e., degree and radian.
Degree: It is the most standard unit to measure an angle. The degree symbol is represented by °. So, an angle of 60 degrees would be written as 60°. Furthermore, a degree can also be divided into minutes and seconds. One degree is equal to 60 minutes (1° = 60') and one minute is equal to 60 seconds (1' = 60").
Radian: This is another important unit of measure. Angles can also be measured and represented in radians that is by using pi (π). Hence, an angle measuring 180 degrees is equal to π in radians. So, 360 degrees would be the same as 2π in radians.
Fun Activity!
As promised, we have a little fun activity for you since you are a few more steps away from being a pro in angles. There are four objects in the table below. Choose the one/s that have an angle/angles.
Look around your house. Can you find more such objects that have angles? Draw them in your notebook.
Types of Angles
Now that we have learnt about the definition and parts of an angle and know how to measure it, let’s take a look at some of the types of angles. When classifying angles, their measurement is the deciding factor. It determines the type of angle. Let us discuss the six major types of angles in Geometry.
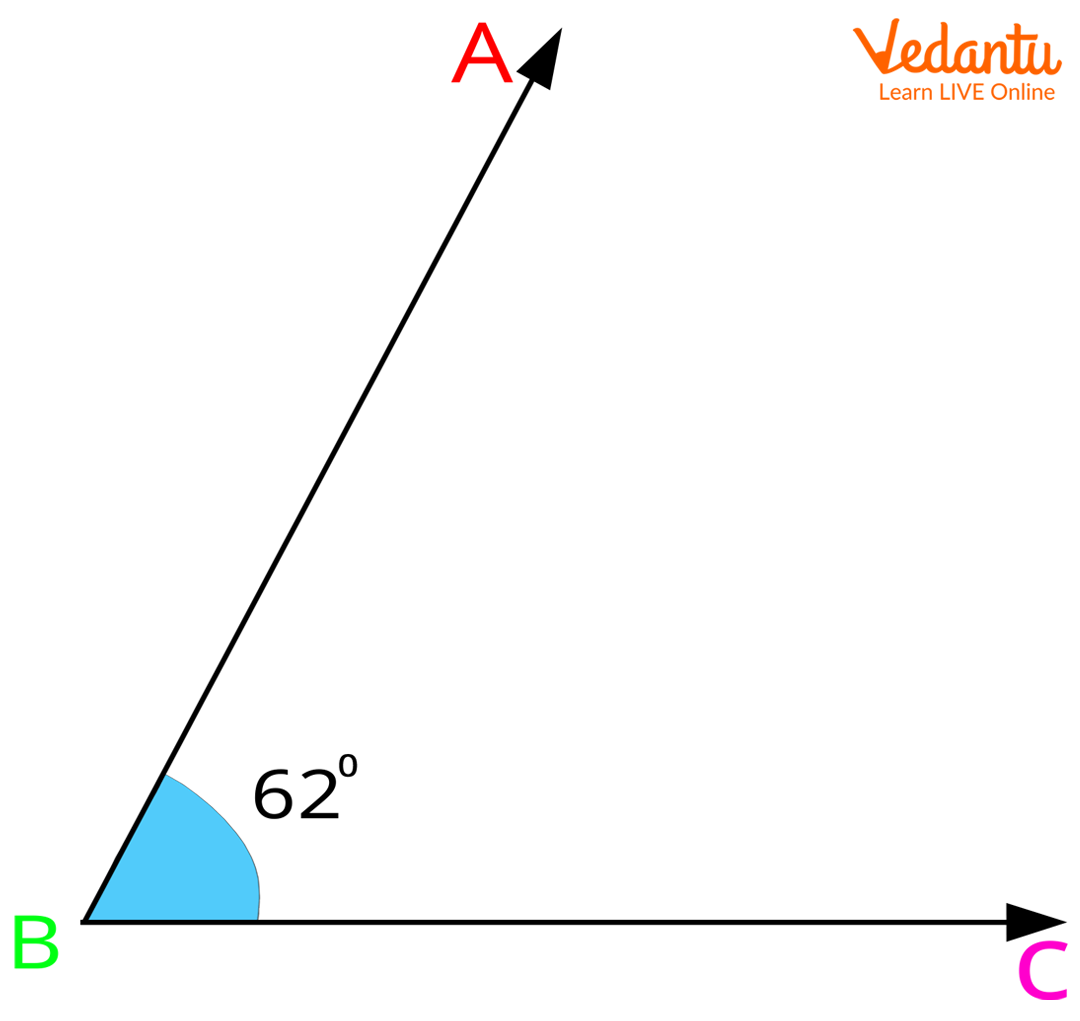
Acute angle: An acute angle is greater than 0° but less than 90°.
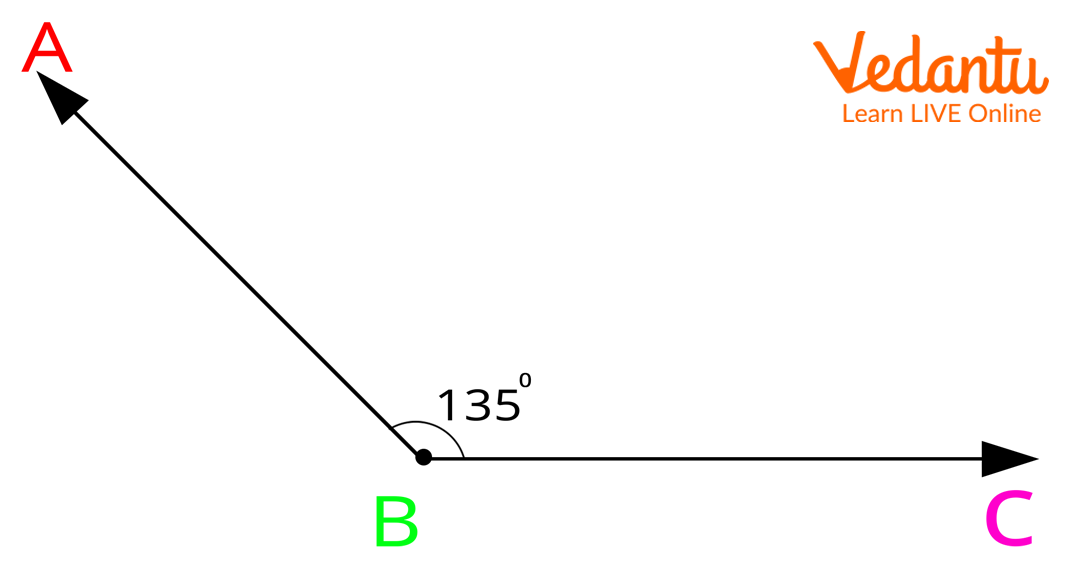
Obtuse angle: Any angle that is greater than 90° but less than 180° is considered an obtuse angle.
Right angle: The right angle is the angle that measures 90 degrees.
Straight angle: The angle measuring 180 degrees is known as the straight angle.
Reflex angle: A reflex angle should be greater than 180° but less than 360°.
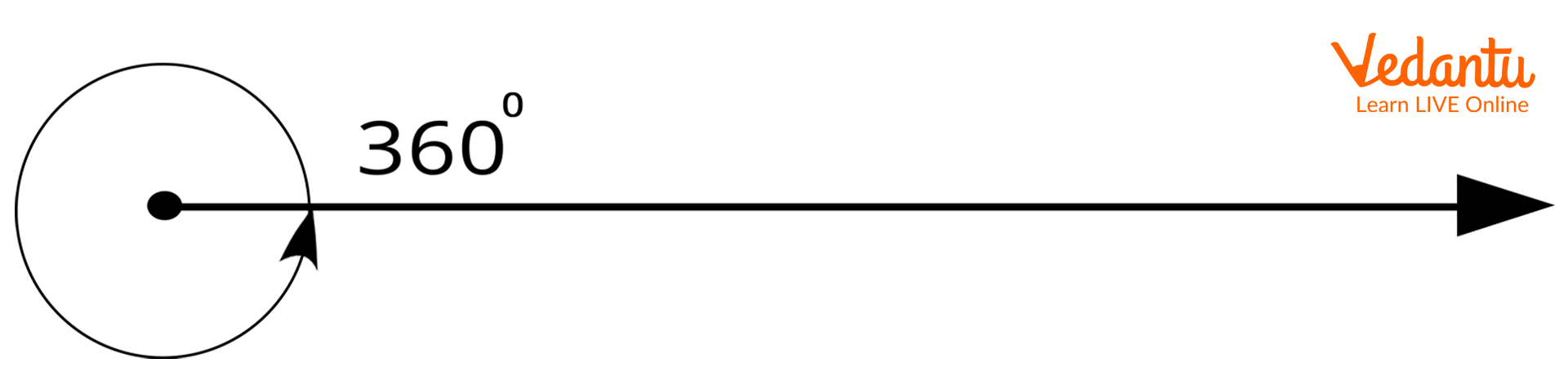
Complete angle: An angle that forms a full circle and measures 360° is known as a complete angle.
2 Bonus Angles!
Here are two more types of angles for you. These include the positive angle and the negative angle.
A positive angle is an angle measured in the anti-clockwise or counterclockwise direction.
A negative angle, on the other hand, is the one that is measured in the clockwise direction.
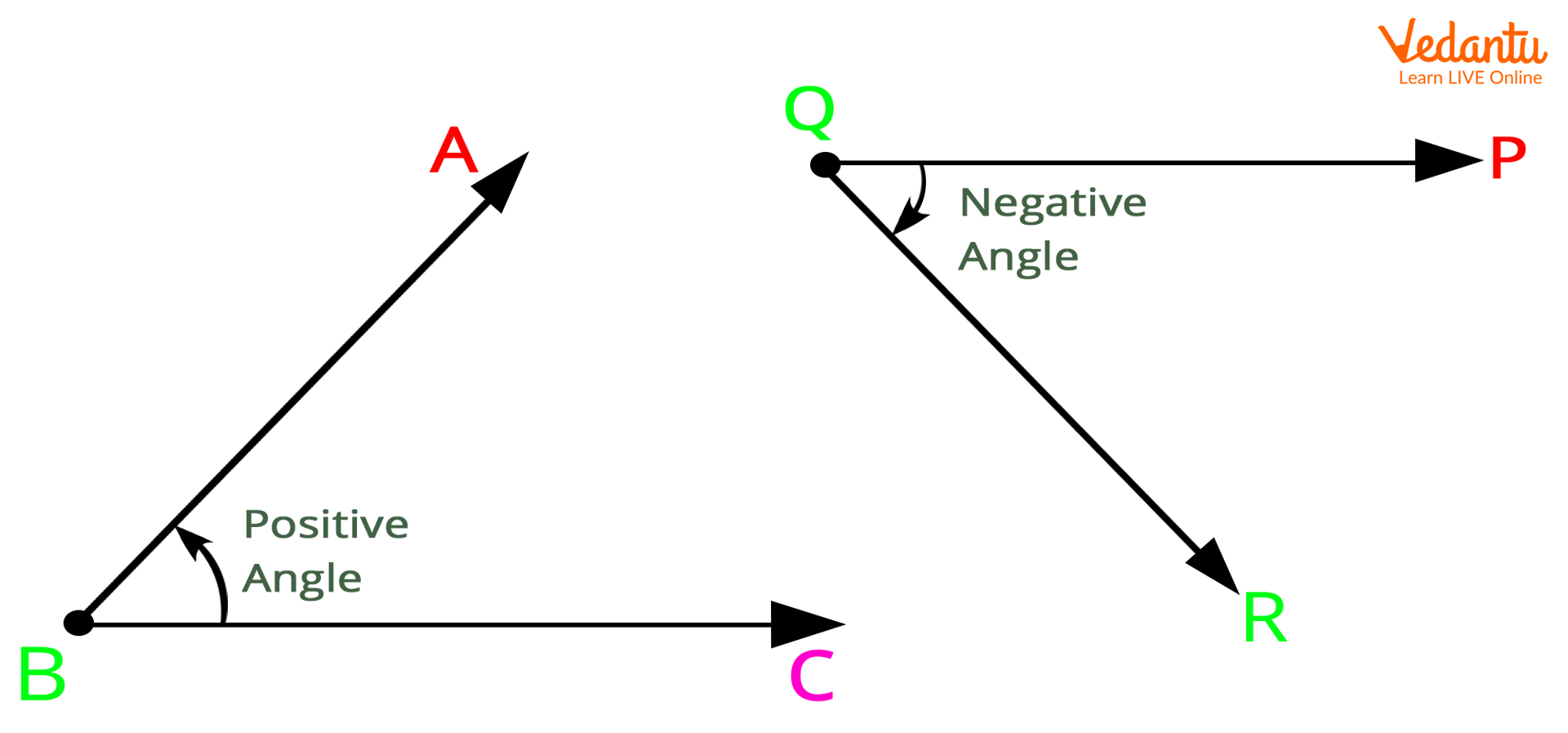
Image: Positive angle and negative angle
Quiz Hour
Learning in itself is incomplete unless we absorb and retain the information we have gathered. Now that we are almost towards the end of the topic, let us revise all that we have learnt about angles through this short and easy quiz. Given below are five questions and three options for each question. Choose the correct answer from what you can recall.
Q1. Which of the following is the angle symbol?
∠ (b) ° (c) π
Q2. The common end point where the arms of an angle meet is the______.
radian (b) vertex (c) protractor
Q3. If you have to measure the size of an angle, which of the following units would you use?
kilograms (b) seconds (c) degrees
Q4. A straight angle measures 180° and a complete angle measures 360°. Is the statement true?
true (b) false (c) partly true
Q5. A positive angle is measured in _____ direction and a negative angle in ____ direction.
clockwise, anti-clockwise (b) anti-clockwise, clockwise (c) clockwise, clockwise
In case you couldn’t remember a few answers, here are all the correct options. Check how many you got correct.
Q1. (a) ∠
Q2. (b) vertex
Q3. (c) degrees
Q4. (a) true
Q5. (b) anti-clockwise, clockwise
Conclusion
So we hope you have gathered a clear picture of what an angle is, the angle symbol, the various parts of an angle, the measurement of angles and the different types of angles. And we hope you had fun too! To learn more about such interesting concepts, head to our website and explore the different articles and worksheets we have prepared for you.
FAQs on Angle Symbol in Maths Explained Clearly
1. What is the angle symbol in mathematics?
The angle symbol in mathematics is ∠, and it is used to represent an angle formed by two rays meeting at a common point. An angle is written as ∠ABC, where:
- B is the vertex (middle letter).
- BA and BC are the arms (rays) of the angle.
2. How do you type the angle symbol (∠) on a keyboard?
The angle symbol ∠ can be typed using special character codes or symbol menus depending on your device. Common methods include:
- Windows: Hold Alt and type 8736 on the numeric keypad.
- Microsoft Word: Insert → Symbol → Choose ∠.
- Copy and paste directly: ∠
3. What does the angle symbol (∠) represent in geometry?
The angle symbol ∠ represents the measure of rotation between two intersecting rays. In geometry, it indicates:
- The vertex where two rays meet.
- The opening between the rays.
- The angle’s measurement in degrees (°) or radians.
4. How do you name an angle using the angle symbol?
An angle is named by writing three points with the vertex in the middle, preceded by the angle symbol ∠. The correct format is:
- ∠ABC
- B is the vertex.
- The sides are BA and BC.
5. What is the difference between the angle symbol (∠) and the degree symbol (°)?
The angle symbol (∠) names an angle, while the degree symbol (°) shows its measurement. For example:
- ∠ABC refers to the angle itself.
- ∠ABC = 45° states that the angle measures 45 degrees.
6. Can you give an example of using the angle symbol in a math problem?
An example of using the angle symbol is: If ∠ABC = 50° and ∠CBD = 40°, then the total angle ∠ABD = 90°. Step-by-step:
- Given: ∠ABC = 50°
- Given: ∠CBD = 40°
- Total angle: 50° + 40° = 90°
7. What are the different types of angles represented using the angle symbol?
The angle symbol ∠ is used to represent different types of angles based on their measure. These include:
- Acute angle: Less than 90°
- Right angle: Exactly 90°
- Obtuse angle: Between 90° and 180°
- Straight angle: Exactly 180°
- Reflex angle: Between 180° and 360°
8. Why is the angle symbol important in geometry?
The angle symbol (∠) is important because it clearly identifies angles in geometric figures and equations. It helps to:
- Avoid confusion between points and lines.
- Label angles correctly in diagrams.
- Express relationships such as ∠A = ∠B.
9. How is the angle symbol used in trigonometry?
In trigonometry, the angle symbol ∠ is used to define the angle for trigonometric ratios like sine, cosine, and tangent. For example:
- If ∠θ = 30°, then sin 30° = 1/2.
- Trigonometric functions depend on the angle measure.
10. What is the symbol for angle in radians?
There is no separate symbol for an angle in radians; the same angle symbol (∠) is used, but the measurement is written without the degree symbol. For example:
- ∠A = π/2 (in radians)
- ∠B = 90° (in degrees)
