Question

The rms and average value of the voltage wave shown in the figure are:

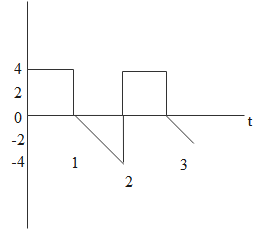
(A) $\sqrt {\dfrac{{32}}{3}} V;1V$
(B) $\sqrt {\dfrac{{11}}{3}} V;1V$
(C) $\sqrt {\dfrac{{11}}{3}} V;3V$
(D) $\sqrt {\dfrac{{32}}{3}} V;3V$

Answer 1

Hint: At first we have to find the rms value of the voltage. For that we should use the formula of square root of the ratio of square sum of the mid ordinate values by the number of ordinates. Once we get the rms value we can find the average value since the rms voltage is equal to the pie divided by $2\sqrt 2 $ into the average voltage. This will give us the required answer.

Complete step by step answer:
We know that the formula to find the rms voltage is given by:
${{\text{V}}_{{\text{rms}}}}{\text{ = }}\sqrt {\dfrac{{{{{\text{(sum of mid ordinate)}}}^{\text{2}}}}}{{{\text{(number of ordinate)}}}}} $
So we have to now put the values from the graph to the above expression. After putting the values, the expression goes as:
${{\text{V}}_{{\text{rms}}}}{\text{ = }}\sqrt {\dfrac{{{4^2} + {4^2}}}{3}} = \sqrt {\dfrac{{32}}{3}} $
As we know that:
${{\text{V}}_{{\text{rms}}}}{\text{ = }}\dfrac{\pi}{{{\text{2}}\sqrt {\text{2}} }}{{\text{V}}_{{\text{avg}}}}{\text{ = 1.11 avg}}$
So now putting the value of ${V_{rms}}$ in the above expression to get:
$ \Rightarrow \sqrt {\dfrac{{{\text{32}}}}{{\text{3}}}} {\text{ V = 0.11 }}{{\text{V}}_{avg}}$
So we can say that:
$ \Rightarrow {V_{avg}} = \dfrac{{\sqrt {32/3} }}{{1.11}} = 2.97 \simeq 3V$
Hence we can say that the rms and average value of the voltage wave shown in the figure are
$\sqrt {\dfrac{{32}}{3}} V;3V$.

So the correct answer is option D.

Note: We should know that the rms value is defined as the square root of the mean or we can say the average value of the square function of the value at that instant. As we know that Ac voltage rises and falls along with the time, it will take more AC voltage to produce a specific rms voltage as compared to that of DC.
The average voltage of a specific periodic waveform may be sine wave or square wave or even in case of triangular wave is defined as the quotient of the area which is present under the waveform in respect to the time.