Question

Let \[x\], \[y\] and \[z\] be positive real numbers. Suppose \[x\], \[y\] and \[z\] are the lengths of the sides of a triangle opposite to its angles \[X\], \[Y\]and \[Z\] respectively. If \[\tan \dfrac{X}{2} + \tan \dfrac{Z}{2} = \dfrac{{2y}}{{x + y + z}}\], then which are the that are statements is/are true?
A.\[2Y = X + Z\]
B.\[Y = X + Z\]
C.\[\tan \dfrac{X}{2} = \dfrac{x}{{y + z}}\]
D.\[{x^2} + {z^2} - {y^2} = xz\]

Answer 1

Hint: To solve the question, we will use the formulas of properties of triangles, Like semi-perimeter of triangle, i.e., \[2S = x + y + z\], and area of triangle with the sides of the triangle \[x\], \[y\]and \[z\]i.e., \[\Delta = \sqrt {s(s - x)(s - y)(s - z)} \] and using \[\tan \dfrac{X}{2} = \dfrac{\Delta }{{s(s - x)}}\], and after simplifying we will get the required result.

Formula Used:
We will use the formula properties of triangles,
\[\Delta = \sqrt {s(s - x)(s - y)(s - z)} \]
\[2S = x + y + z\]
\[\tan \dfrac{X}{2} = \dfrac{\Delta }{{s(s - x)}}\], \[\tan \dfrac{Z}{2} = \dfrac{\Delta }{{s(s - z)}}\],
\[\tan \dfrac{X}{2} = \sqrt {\dfrac{{(s - y)(s - z)}}{{s(s - x)}}} \], where\[x\], \[y\]and \[z\]are the sides of the triangle.
\[{\left( {a + b} \right)^2} + {\left( {a - b} \right)^2} = 2\left( {{a^2} + {b^2}} \right)\].

Complete Step-by-Step Solution:
Given that\[x\], \[y\]and \[z\] be positive real numbers. Suppose\[x\], \[y\]and \[z\] are the lengths of the sides of a triangle opposite to its angles\[X\], \[Y\]and \[Z\], respectively, and \[\tan \dfrac{X}{2} + \tan \dfrac{Z}{2} = \dfrac{{2y}}{{x + y + z}}\],
Let, \[2S = x + y + z\] and
\[\tan \dfrac{X}{2} + \tan \dfrac{Z}{2} = \dfrac{{2y}}{{x + y + z}}\]
\[ \Rightarrow \dfrac{\Delta }{{s(s - x)}} + \dfrac{\Delta }{{s(s - z)}} = \dfrac{{2y}}{{2s}}\]
Now we will simplify, we will get,
\[ \Rightarrow \dfrac{\Delta }{s}\left( {\dfrac{{2s - (x + z)}}{{\left( {s - x} \right)\left( {s - z} \right)}}} \right) = \dfrac{y}{s}\]
Now we will further simplify,
\[ \Rightarrow \Delta \left( {\dfrac{{x + y + z - (x + z)}}{{\left( {s - x} \right)\left( {s - z} \right)}}} \right) = y\]
Now we will eliminate the like terms,
\[ \Rightarrow \Delta \left( {\dfrac{y}{{\left( {s - x} \right)\left( {s - z} \right)}}} \right) = y\]
Now we will further simplify,
\[ \Rightarrow \Delta = \left( {s - x} \right)\left( {s - z} \right)\]
Now we will square on both sides,
\[ \Rightarrow {\Delta ^2} = {\left( {s - x} \right)^2}{\left( {s - z} \right)^2}\]
Now we will use the formula, \[\Delta = \sqrt {s(s - x)(s - y)(s - z)} \]
\[ \Rightarrow {\left( {\sqrt {s(s - x)(s - y)(s - z)} } \right)^2} = {\left( {s - x} \right)^2}{\left( {s - z} \right)^2}\]
Now we will simplify, we will get,
\[ \Rightarrow \left( {s(s - x)(s - y)(s - z)} \right) = {\left( {s - x} \right)^2}{\left( {s - z} \right)^2}\]
Now we will eliminate the like terms,
\[ \Rightarrow \left( {s(s - y)} \right) = \left( {s - x} \right)\left( {s - z} \right)\]
Now we will use the formula, \[2S = x + y + z\],
\[ \Rightarrow \left( {\dfrac{{x + y + z}}{2}} \right)\left( {\dfrac{{x + y + z}}{2} - y} \right) = \left( {\dfrac{{x + y + z}}{2} - x} \right)\left( {\dfrac{{x + y + z}}{2} - z} \right)\]
Now we will simplify,
\[ \Rightarrow \left( {x + y + z} \right)\left( {x + z - y} \right) = \left( {y + z - x} \right)\left( {x + y - z} \right)\]
Now we will simplify,
\[ \Rightarrow {\left( {x + z} \right)^2} - {y^2} = {y^2} - {\left( {z - x} \right)^2}\]
Now we will further simplify we will get,
\[ \Rightarrow {\left( {x + z} \right)^2} + {\left( {z - x} \right)^2} = 2{y^2}\]
Now we will use the formula, \[{\left( {a + b} \right)^2} + {\left( {a - b} \right)^2} = 2\left( {{a^2} + {b^2}} \right)\]
\[ \Rightarrow 2\left( {{x^2} + {z^2}} \right) = 2{y^2}\]
Now we will eliminate the like terms,
\[ \Rightarrow {x^2} + {z^2} = {y^2}\],
Now the above equation is in form of Pythagorean Theorem, with right triangle at Y,
By drawing the diagram,

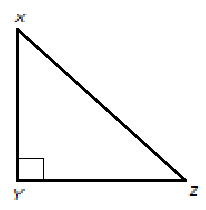
Now using the formula \[\tan \dfrac{X}{2} = \dfrac{\Delta }{{s(s - x)}}\],
\[ \Rightarrow \tan \dfrac{X}{2} = \dfrac{\Delta }{{s(s - x)}} = \dfrac{{\dfrac{1}{2}xz}}{{\dfrac{{{{\left( {y + z} \right)}^2} - {x^2}}}{4}}}\]
As we can say_,
\[s - x = \dfrac{{x + y + z}}{2} - x\]
\[ = \dfrac{{}}{{}}\] \[\dfrac{{y + z - x}}{2}\]
\[s(s - x) = \left( {\dfrac{{y + z + x}}{2}} \right)\left( {\dfrac{{y + z - x}}{2}} \right)\]
=\[\dfrac{{{{\left( {y + z} \right)}^2} - {x^2}}}{4}\]
\[ \Rightarrow \tan \dfrac{X}{2} = \dfrac{{\dfrac{1}{2}xz}}{{\dfrac{{{{\left( {y + z} \right)}^2} - {x^2}}}{4}}}\]
Now we will simplify, we will get,
\[ \Rightarrow \tan \dfrac{X}{2} = \dfrac{{2xz}}{{{y^2} + {z^2} + 2yz - {x^2}}}\]
Now we know that, \[{y^2} = {x^2} + {z^2}\],
\[ \Rightarrow \tan \dfrac{X}{2} = \dfrac{{2xz}}{{2{z^2} + 2yz}}\]
Now we will simplify then we will get,
\[ \Rightarrow \tan \dfrac{X}{2} = \dfrac{{2xz}}{{2z\left( {z + y} \right)}}\]
Now eliminating the like terms,
\[ \Rightarrow \tan \dfrac{X}{2} = \dfrac{x}{{z + y}}\]
And,
One angle is the right angle then the other two angles give a sum equal to 90 degrees because all angles of the triangle sum up 180 degrees. Therefore option B is correct.

The correct option is B and C.

Note If we know the three sides and three angles of a triangle, then we can know completely about the triangle, thus if we know any of the three elements such as two angles and one side we can find the other elements using the formulae. This process is called the solution of triangles.