Parallel First-Order Reaction - JEE Important Topic

Chemical Kinetics is one of the most critical branches of study. It can seem analogous to thermodynamics but is refined in the way of reactions being balanced and rates being described properly. Before describing the order of a reaction, we must know what reaction rate is and how it is so important for defining a reaction properly. Reaction rate is nothing but the rate at which a certain reaction takes place. It tells us how sooner a reaction will finish or how lengthy it is going to be. This rate mathematically increases with the increase in the rate of product concentration and diminishing rate of reactant concentration.

Now, what is a parallel reaction? In Chemistry, parallel reactions, also known as side reactions, are the reactions in which the decay of substances when reacting can do so in two ways, or more ways. A chemical reaction that has a reaction rate that is linearly dependent on the concentration of just one ingredient is known as a first-order reaction. In other terms, a first-order reaction is a chemical reaction in which only one of the reactants' concentrations changes and the rate of the reaction changes as a result.

Graphical Representation of a First-Order Reaction

The graph below shows the concentration versus time for a first-order reaction.

Concentration v/s Time Graph for a First Order Reaction

For first-order reactions, the equation $\ln [A]=-kt+\ln {{[A]}_{0}}$  is similar to that of a straight line (y = mx + c) with slope -k. The following graphic shows how to plot this line:

$ln[A]$ v/s Time Graph of a First Order Reaction

Thus, the graph for $ln[A]$ v/s t for a first-order reaction is a straight line with slope -k.

Examples of First-Order Reactions

• $S{{O}_{2}}C{{l}_{2}}\to C{{l}_{2}}+S{{O}_{2}}$ 

• $2{{N}_{2}}{{O}_{5}}\to {{O}_{2}}+4N{{O}_{2}}$ 

• $2{{H}_{2}}{{O}_{2}}\to 2{{H}_{2}}O+{{O}_{2}}$ 

Simultaneous Reactions

Two further categories of simultaneous reactions exist in addition to the opposite or reversible ones: sequential and parallel reactions. Only the kinetic profiles of these two types of reactions up to the first order will be covered in this section.

Consecutive or Sequential Reactions

The sequence of the reaction has frequently not been found to match the molecularity indicated by the stoichiometry in complex reactions. Therefore, rather than occurring in a single step, these reactions must occur in several steps. Each of these many phases is referred to as a sequential reaction.

The single-step reactions that can be formulated to describe an overall reaction are sometimes referred to as the successive reactions. Consider two first-order reactions in which reactant A changes into product B, which then changes into C to understand the kinetic profile of subsequent reactions.

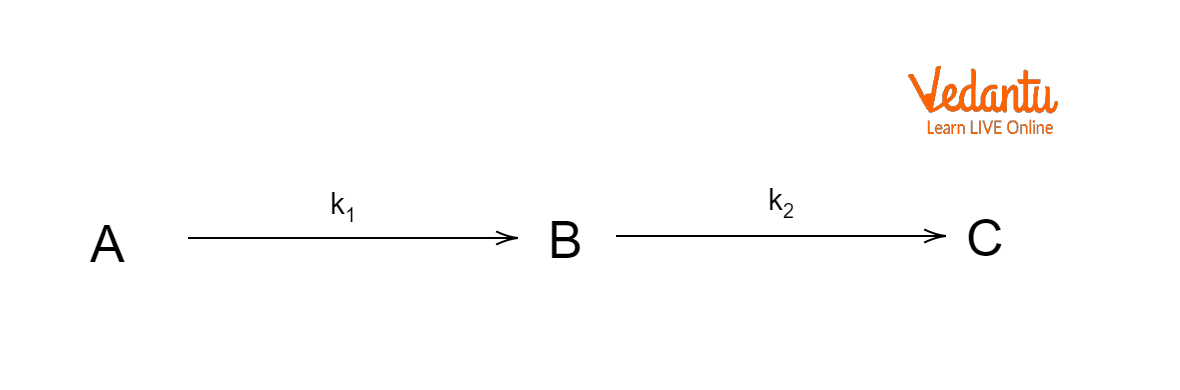
Consecutive or Sequential Reactions

Where ${{k}_{1}}$ and ${{k}_{2}}$ are the rate constants for the first and second steps, respectively. To put it another way, A is the reactant, B is just an intermediary step, and C is the outcome. However, ${{k}_{1}}$ and ${{k}_{2}}$ have comparable values, a rate law depending upon both the constants can be written. Now suppose that the initial concentrations of reactant A is ${{C}_{0}}$, while the concentrations of A, B, and C after time t are ${{C}_{A}}$ , ${{C}_{B}}$, and ${{C}_{C}}$, respectively. So, we can say that

${{C}_{0}}={{C}_{A}}+{{C}_{B}}+{{C}_{C}}$

Parallel First-Order Reaction

In many reactions, the reactant interacts to concurrently produce more than one product. We can simply disregard the other reactions if the amount of one reaction product is very large compared to the others. We must adjust the general rate equation to account for this, though, if the quantity of the product generated by other reactions is appreciably large. The reactions where several starting species react at once to produce different products are known as parallel or side reactions.

Parallel First-Order Kinetics

Consider a situation where a reactant A reacts simultaneously to produce products B and C in order to better grasp the kinetics of parallel reactions of the first order. Below is a typical illustration of a parallel or side reaction with two routes.

Parallel First Order Reactions

Where ${{k}_{1}}$ and ${{k}_{2}}$ are the rate constants. Assume now that a represents the reactant A's initial concentration and x represents the reactant's decline in concentration over the course of "t" time. Hence, the rates of first (${{R}_{1}}$) and second reaction (${{R}_{2}}$) can be given as:

${{R}_{1}}=\dfrac{d[B]}{dt}={{k}_{1}}[A]={{k}_{1}}(a-x)$                                          ----(1)

Or

${{R}_{2}}=\dfrac{d[C]}{dt}={{k}_{2}}[A]={{k}_{2}}(a-x)$                                ----(2)

Equations (1) and equation (2) together can be used to calculate the overall reaction rate.

$\dfrac{dx}{dt}=\dfrac{d[B]}{dt}+\dfrac{d[C]}{dt}={{k}_{1}}(a-x)+{{k}_{2}}(a-x)$ 

$\Rightarrow \dfrac{dx}{dt}=({{k}_{1}}+{{k}_{2}})(a-x)$ 

$\Rightarrow \dfrac{dx}{(a-x)}=({{k}_{1}}+{{k}_{2}})dt$                                               ----(3)

Equation (3) is integrated, then rearranged to yield

${{k}_{1}}+{{k}_{2}}=\dfrac{1}{t}\ln \dfrac{a}{a-x}$                                                    -----(4)

Moreover, when we divide equation (1) by (2), we obtain

$\dfrac{{{R}_{1}}}{{{R}_{2}}}=\dfrac{{{k}_{1}}(a-x)}{{{k}_{2}}(a-x)}$

$\Rightarrow \dfrac{{{R}_{1}}}{{{R}_{2}}}=\dfrac{{{k}_{1}}}{{{k}_{2}}}$                                                        -----(5)

Hence, the value of rate constants involved, i.e., ${{k}_{1}}$ and ${{k}_{2}}$, can easily be obtained from the use of equation (4) and equation (5).

Concentration v/s Time Graph for Parallel First Order Reactions 

Example of Parallel Reaction and Consecutive Reaction

Examples of parallel reactions are (1) nitration of phenol with the formation of ortho-, meta-, and Para-nitrophenol (identical reactants) and (2) nitration of a benzene and toluene mixture (nitric acid is the common reactant). Examples of consecutive reactions are (1) decomposition of ethylene oxide and (2) the pyrolysis of acetone.

Conclusion

First-order reactions are the reactions in which the reaction rate is only dependent on the reactant concentration. To put it another way, the reaction rate doubles when the concentration of the reactant does. To put it another way, the reaction rate doubles when the concentration does. One or two reactants can be present in a first-order reaction, as in the case of the decomposition process. If the first-order reactant concentration is doubled in these reactions, the reaction rate will likewise double. Similar to this, a fivefold increase in the first-order reactant concentration will result in a 500% rise in reaction rate.

Parallel or side reactions are those in which a substance changes or decomposes in more than one way. The reactants take one or two pathways to produce more products. The reaction rate can be adjusted by altering the reaction conditions like pressure, temperature, catalyst etc. The conditions when optimised produce the greatest yield of products and the other reactions then fall into the category of side or parallel reactions. Parallel reactions should not be confused with the idea of successive reactions. When two reactions take place concurrently and produce two or more distinct products, this is referred to as a parallel reaction.