




Key Equations and Real-Life Examples of Uniform Pure Rolling
The concept of Uniform Pure Rolling is extremely important in rigid body dynamics, especially for students preparing for JEE Physics. Pure rolling describes a condition where a body rolls without slipping, and uniform pure rolling means the velocity of rolling is constant throughout the motion.
Rolling Motion: Overview
Rolling motion combines translational and rotational movements. The center of mass of the body moves forward, and at the same time, the object rotates about its axis. This motion is seen in wheels, balls, and cylinders traveling on a surface.
Pure Rolling Explained
Pure rolling is observed when the contact point between a rolling body and the surface has zero velocity relative to the surface. This happens only when the condition v = Rω is satisfied, where v is the linear velocity of the center of mass, R is the radius, and ω is the angular velocity.
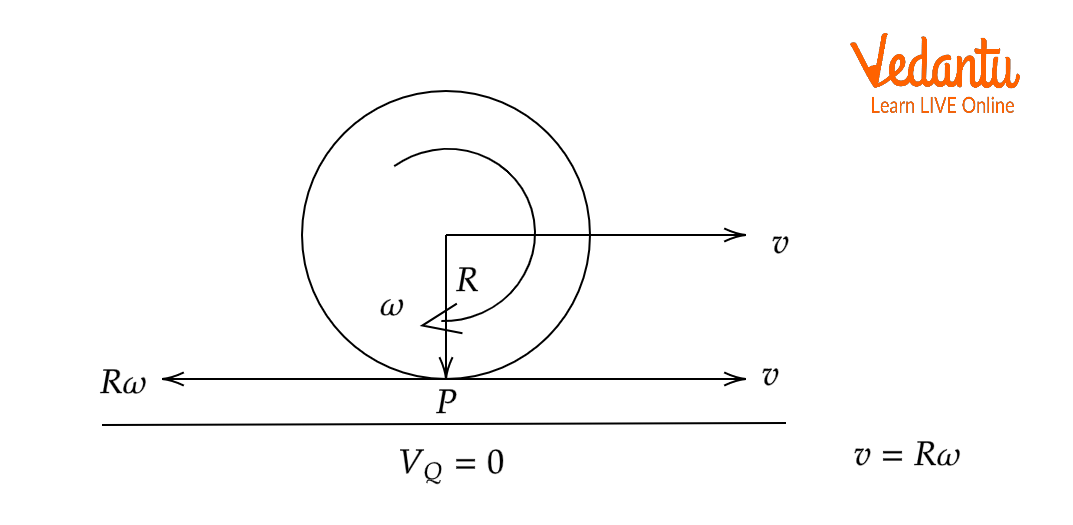
In real-life examples such as a car’s wheel rolling on a road or a solid sphere moving on a horizontal table, pure rolling ensures no part of the surface slips. If this no-slip condition is maintained, the rolling is considered ‘pure’.
Uniform Pure Rolling Motion
In case of uniform pure rolling, both the linear velocity and angular velocity remain constant, meaning no external torque or net force acts on the body. The frictional force is just enough to prevent slipping but does no work, since the point of contact remains momentarily at rest with respect to the surface. This is why energy loss due to friction is negligible in pure rolling.
Mathematical Condition for Pure Rolling
For pure rolling, two velocities at the contact point are considered: one from translational motion, and another from rotational motion. These velocities are equal and opposite in direction at the point touching the surface, resulting in zero net velocity at that point.
- The translational contribution is equal to v (center of mass velocity).
- The rotational contribution is equal to Rω (R times angular velocity).
- Pure rolling exists when v = Rω always.
When the relationship between v and ω is not maintained, slipping occurs. This type of motion is called non uniform pure rolling or simply rolling with slipping.
Difference Between Rolling and Pure Rolling
Ordinary rolling motion can involve slipping between the body and surface, which results in energy being lost to heat due to kinetic friction. In contrast, pure rolling ensures there is no relative movement at the point of contact, which eliminates frictional work and helps preserve total mechanical energy.
| Rolling Motion | Pure Rolling |
|---|---|
| May involve slipping | No slipping occurs |
| Both static and kinetic friction present | Only static friction at contact point |
| Energy loss possible | No energy loss due to friction |
| Condition v ≠ Rω possible | Condition v = Rω always |
Example: Rolling Without Slipping
Consider a disc of radius R rolling on a fixed surface without slipping. Its center of mass has velocity v, and it rotates with angular velocity ω. The point of contact's total velocity is always zero relative to the ground, perfectly illustrating the concept of pure rolling.
Kinetic Energy in Uniform Pure Rolling
When a body is in uniform pure rolling, it has both translational kinetic energy and rotational kinetic energy about its center of mass. The total kinetic energy is the sum of these two components:
- Translational K.E. = (1/2) m v2
- Rotational K.E. = (1/2) I ω2
Here, m is the mass and I is the moment of inertia about the center of mass. Applying the condition v = Rω, the total energy can be re-expressed for different shapes, which is important for solving uniform pure rolling motion problems in exams.
Pure Rolling for Various Bodies
Depending on the object's geometry, the partitioning of kinetic energy changes. For uniform rings, solid discs, hollow spheres, and solid spheres, the moment of inertia values differ and affect their rolling properties.
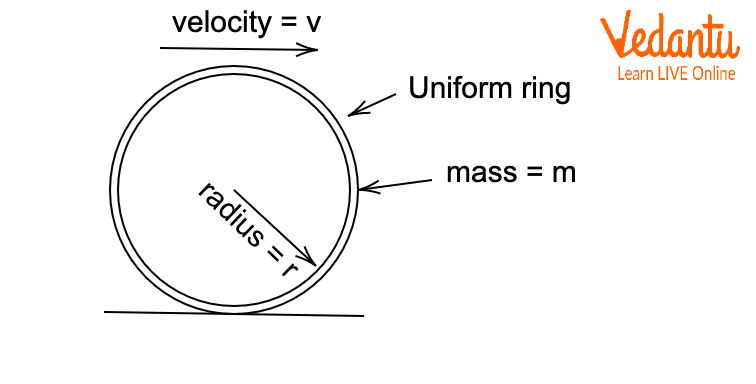
A uniform ring exhibits the highest rotational energy portion relative to its total kinetic energy compared to other bodies under pure rolling. This subtly impacts questions involving energy distribution and final speeds.

A uniform solid disc shows a greater proportion of kinetic energy in translation than a ring under the same pure rolling conditions. This characteristic matters for problems involving pure rolling 1 and pure rolling 2 in JEE exams.
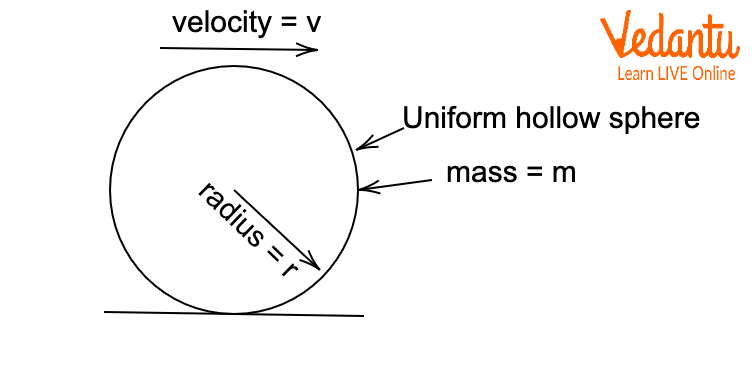
A uniform hollow sphere's moment of inertia results in a kinetic energy partition intermediate between a ring and a solid sphere, and impacts its acceleration down an inclined plane.
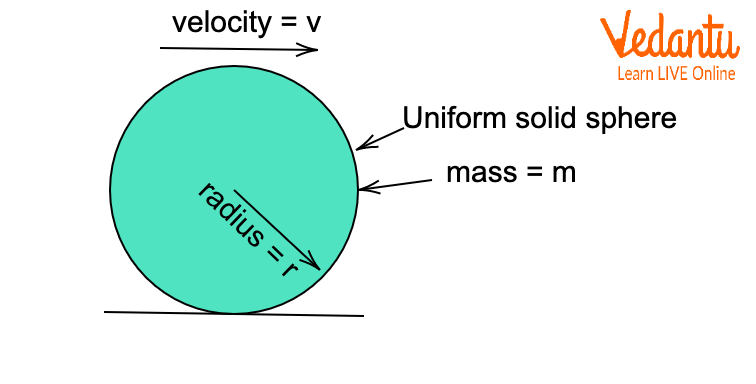
A uniform solid sphere’s smaller moment of inertia allows for the highest acceleration and least rotational contribution among round objects rolling without slipping, making it a good pure rolling example for exam questions.
Effect of Friction in Uniform Rolling
In uniform pure rolling, static friction is present but does no work, because the instantaneous point of contact does not slide. If friction was absent, pure rolling could not be maintained. If the friction is exceeded, non uniform pure rolling or slipping occurs.
Common Applications and Examples
Understanding pure rolling helps explain why round objects descend slopes effectively and why wheels are used in machines for high efficiency. Real-world examples include moving car tires and bowling balls on smooth tracks.
You can explore related physics topics like circular motion or deepen your understanding via the kinematics section.
FAQs on Understanding Uniform Pure Rolling in Physics
1. What is uniform pure rolling?
Uniform pure rolling occurs when a body, like a wheel or cylinder, rolls on a surface without slipping, and its linear velocity remains constant.
- In pure rolling, the point of contact with the surface is instantaneously at rest.
- The relationship between translation and rotational motion is v = rω, where v is linear velocity, r is radius, and ω is angular velocity.
- This motion features both non-slipping condition and uniform velocity.
2. What are the conditions necessary for pure rolling?
For an object to exhibit pure rolling, certain key conditions must be satisfied:
- The object must not slip at the point of contact, ensuring the velocity of the contact point is zero relative to the surface.
- The linear velocity of the object’s center, v, must equal rω (radius multiplied by angular velocity).
- There must be a balance between rotational and translational motion.
3. What is the difference between pure rolling and pure sliding?
Pure rolling and pure sliding are two distinct types of motion for rigid bodies.
- In pure rolling, the point of contact is instantaneously at rest, with v = rω.
- In pure sliding (slipping), the object moves only translationally, and v ≠ rω; there is no rotation matching the translation.
- Rolling combines rotation with translation, but sliding involves only translation.
4. State the velocity of the point of contact for a body in pure rolling motion.
In pure rolling motion, the velocity of the point of contact with the surface is always zero relative to the surface.
- The lower most point on the rolling body is momentarily at rest.
- This satisfies the no-slip condition typical of pure rolling.
5. How can you determine whether an object is undergoing pure rolling?
To check if an object is in pure rolling:
- Verify that the velocity of the point of contact with the ground is zero at every instant.
- Check if v = rω holds true for linear and angular velocities.
- Observe if the object moves without leaving any slips or skids on the surface.
6. What are some examples of pure rolling from daily life?
Some common examples of pure rolling include:
- A wheel rolling straight on a level road without skidding.
- A ball rolling smoothly across the floor.
- A car tyre moving without slipping on the road.
7. Derive the relationship between linear velocity and angular velocity in pure rolling.
In pure rolling, the linear velocity (v) of the center of mass and the angular velocity (ω) are connected by the equation:
- v = rω, where r is the radius of the rolling object.
- This ensures the speed at the bottom point is zero, fulfilling the pure rolling condition.
8. What happens if the condition v = rω is not satisfied during rolling?
If v ≠ rω during rolling, the object will experience slipping at the point of contact.
- This is called rolling with slipping.
- The relative motion between the object and the surface introduces frictional losses.
- Pure rolling motion is no longer maintained.
9. What is the kinetic energy of a body under uniform pure rolling?
The total kinetic energy of a body in uniform pure rolling is the sum of translational and rotational energies:
- Translational KE: (½)mv², where m is mass and v is linear velocity.
- Rotational KE: (½)Iω², where I is the moment of inertia and ω is angular velocity.
- Since v = rω, KE can also be written as a function of either v or ω.
10. Why is static friction important in pure rolling?
Static friction enables pure rolling by preventing relative motion between the rolling object and the surface at the point of contact.
- It ensures the no-slip condition—the essential criterion for pure rolling.
- Without sufficient static friction, pure rolling cannot occur, as the object would begin to slip.
























