




Simple Rules for Applying Sign Convention in Ray Diagrams
The sign convention of lens and mirror forms the foundation for solving optics questions in physics, especially when tackling JEE and board examinations. Using the correct sign rules ensures accuracy in calculation and conceptual understanding.
What the Sign Convention Means in Optics
Sign convention in optics helps us assign positive or negative values to distances, focal lengths, and heights when studying lenses and mirrors. It provides consistency in ray diagrams and mathematical formulas.
The concept uses the Cartesian coordinate system. Here, the optical center for lenses or pole for mirrors serves as the origin, with the principal axis acting as the reference line for all measurements.
Setting Up the Axis and Direction in Sign Convention
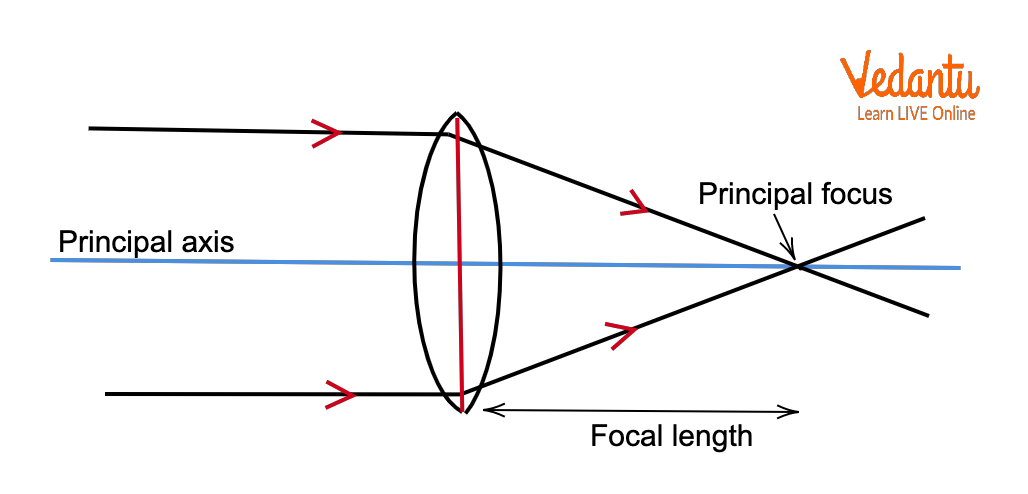
Light is conventionally considered to travel from left to right along the principal axis. This standard direction is vital for all sign convention rules applied in lens and mirror questions.
Distances measured towards the right (incident ray direction) are positive. All distances measured to the left (against the incident ray direction) are negative. This forms the basis for all further sign assignments.
Key Rules for the Sign Convention of Lens and Mirror
For both lenses and mirrors, specific rules assign the sign to object distance, image distance, focal length, and height. These guidelines stay consistent for both concave and convex varieties with slight adjustments for their focal lengths.
Object distance (u) is nearly always negative because the object is positioned to the left of the mirror or lens, opposite to the direction of incident light. Remember this for every ray diagram or calculation you perform.
Heights and Image Types in the Sign Convention
Heights above the principal axis are positive, representing erect images, while heights below are negative, showing inverted images. Upright and inverted formations must be distinguished for correct magnification calculations.
How Focal Length Differs: Concave vs. Convex Lens and Mirror
For concave mirrors or concave lenses, the focal length (f) is always negative, as the focus lies to the left of the origin. For convex mirrors and convex lenses, focal length is positive since the focus lies to the right.
The signs for real and virtual images also follow this pattern. Real images form on the same side as the object and take negative signs. Virtual images, forming on the opposite side, are given positive signs.
Difference Between Lens and Mirror Sign Convention
While sign conventions are based on the same principles for both devices, the reference point differs. Lenses use the optical center, while mirrors use the pole as the origin for distance measurement.
The directionality of incident light remains consistent for both. However, physical constructions may slightly shift the interpretation of positive and negative image placements in certain diagrams.
Lens and Mirror Sign Convention Table
| Quantity | Sign Assignment |
|---|---|
| Object Distance (u) | Negative (left of origin) |
| Image Distance (v, real) | Negative (left of mirror/lens) |
| Image Distance (v, virtual) | Positive (right of mirror/lens) |
| Focal Length (f, concave) | Negative |
| Focal Length (f, convex) | Positive |
| Height above axis | Positive (erect) |
| Height below axis | Negative (inverted) |
Applying the Sign Convention in Mirror and Lens Formulas
Sign convention becomes crucial for any calculation involving the lens or mirror formula. Mistakes in sign assignment may yield incorrect image position, type, or magnification.
For spherical mirrors, the formula is:
$ \dfrac{1}{f} = \dfrac{1}{v} + \dfrac{1}{u} $
For thin lenses, the formula is:
$ \dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{u} $
Correct sign usage with both formulas ensures that physics principles and results align perfectly.
For more details on lens sign rules, visit the Sign Convention In Lenses page which deepens understanding of this concept.
A Real-Life Analogy for Visualising Sign Convention
Imagine standing at a railway platform (the origin), and looking along the tracks. Walking away from you is negative, walking towards the town (light's direction) is positive. This analogy helps clarify when to use each sign in optics problems.
Numerical Example: Applying The Sign Convention
Let’s solve: An object is placed $20\,\text{cm}$ in front of a concave mirror with a focal length of $10\,\text{cm}$. Find the image distance ($v$).
Known: object distance $u = -20\,\text{cm}$, focal length $f = -10\,\text{cm}$.
The mirror formula is:
$ \dfrac{1}{f} = \dfrac{1}{v} + \dfrac{1}{u} $
Substituting the given values:
$ \dfrac{1}{-10} = \dfrac{1}{v} + \dfrac{1}{-20} $
$ \dfrac{1}{v} = \dfrac{1}{-10} - \dfrac{1}{-20} $
$ \dfrac{1}{v} = -\dfrac{1}{10} + \dfrac{1}{20} $
$ \dfrac{1}{v} = -\dfrac{2}{20} + \dfrac{1}{20} = -\dfrac{1}{20} $
So, $v = -20\,\text{cm}$. The image forms on the same side as the object, and is real and inverted.
Practice Question: Test Your Understanding of Sign Convention
A convex lens has a focal length of $12\,\text{cm}$. An object is placed $24\,\text{cm}$ to the left of the lens. Using the correct sign convention, calculate the image distance ($v$).
Common Mistakes in Sign Convention of Lens and Mirror
- Assigning the wrong sign to focal length for concave or convex types
- Forgetting object distance is usually negative in ray diagrams
- Swapping signs for real and virtual images in calculation steps
- Mixing up the origin (optical center vs. pole) for measurements
- Misreading the direction of light propagation or principal axis
Real-Life Applications of Sign Convention Principles
Hospital imaging uses sign conventions to predict image location using concave mirrors in devices. Cameras apply lens sign rules for object placement. Telescopes and microscopes also depend on these basic conventions to produce clear, predictable images.
For more on how sign convention leads to correct image size and position results, see Mirror Formula And Magnification for step-by-step examples.
Comparison of Sign Convention in Lens and Mirror
| Aspect | Lens | Mirror |
|---|---|---|
| Reference Point | Optical Center | Pole |
| Incident Light Direction | Left to Right | Left to Right |
| Focal Length (Convex) | Positive | Positive |
| Focal Length (Concave) | Negative | Negative |
Visualizing the Concepts in Advanced Physics Problems
When working with combined lens-mirror systems or complex ray diagrams, the principles above remain unchanged. Always assign signs relative to the kind of optical element and reference point.
To further clarify practical sign issues in ray tracing, see Difference Between Lens And Mirror for diagrams and case studies.
New Cartesian Convention in JEE and Board Exams
The New Cartesian Convention is the modern standard in competitive and board exams. Stick to its rules for all distance and height measurements to avoid loss of marks in numericals and theory.
Explore its application and detailed ray path concepts in Refraction Of Light Through Prism for a deeper foundation.
Mastering the Sign Convention for All Lens and Mirror Types
For quick revision, always sketch the principal axis and clearly mark object and focus positions. This boosts speed during exams and reduces calculation errors. Confidence grows as you solve more questions following these sign principles.
Advanced Problems and Properties with Convex and Concave Lenses
Understanding the sign convention directly informs your approach to questions on the properties of convex and concave systems. You’ll be able to handle complex combinations using the correct rules with ease.
Related Physics Topics for Further Study
Sign convention of lens and mirror class 10
Sign convention for lens and mirror class 12
Sign convention of concave lens and mirror
Sign convention of convex lens and mirror
Difference between sign convention of lens and mirror
Sign convention for lens and mirror class 10 table
Sign convention of concave convex lens and mirror
Sign convention for lens and mirror are same
FAQs on Understanding Sign Convention for Lenses and Mirrors
1. What is the sign convention for lenses in optics?
The sign convention for lenses in optics assigns positive and negative values to distances based on a specific set of rules:
- All distances are measured from the optical centre of the lens.
- Distances measured in the direction of incident light (typically left to right) are considered positive.
- Distances measured opposite to the direction of incident light are negative.
- Heights above the principal axis are positive; below are negative.
- Focal length is positive for convex lenses and negative for concave lenses.
2. What is the sign convention for mirrors?
The sign convention for mirrors helps assign correct signs to object, image, and focal distances:
- Measuring starts from the mirror’s pole (P).
- Distances measured towards the object (usually to the left) are negative.
- Distances measured in the direction of the reflected light (to the right) are positive.
- Focal length of a concave mirror is negative; that of a convex mirror is positive.
- Heights above the principal axis are positive; below are negative.
3. What is the New Cartesian Sign Convention?
The New Cartesian Sign Convention is a standardized system for measuring distances and assigning signs in lens and mirror problems:
- All distances are measured from the pole (mirror) or optical centre (lens) as the origin.
- Distances along the direction of incident light (towards the right) are positive.
- Distances against the direction of incident light (towards the left) are negative.
- Heights above the principal axis are positive; below are negative.
4. Why is sign convention important in ray diagrams?
Sign convention is vital for accurately constructing and interpreting ray diagrams:
- Prevents errors in applying lens and mirror formulas.
- Helps distinguish between real and virtual images.
- Ensures correct prediction of image orientation (erect/inverted).
- Clarifies whether images are on the same or opposite side as the object.
5. What are the key rules of sign convention for spherical mirrors?
The key rules for sign convention for spherical mirrors are as follows:
- Distances measured from the pole (P) of the mirror.
- Object distance (u) is always negative (since the object is placed to the left).
- Image distance (v) is negative if image forms on the same side as the object (real image), positive for the other side (virtual image).
- Focal length (f) is negative for concave mirror, positive for convex mirror.
- Heights above the principal axis are positive; below are negative.
6. How does the sign convention differ for convex and concave lenses?
The sign of focal length distinguishes convex and concave lenses according to the sign convention:
- Convex lens: Focal length is positive because it converges rays on the right side of the lens (along incident light).
- Concave lens: Focal length is negative as it diverges rays to the left (opposite to incident light).
- Object distances are negative, heights above axis are positive, as per the Cartesian system.
7. What are the important points to remember about the sign convention of a concave mirror?
The important points for the sign convention in a concave mirror are:
- Object distance (u): Always negative.
- Image distance (v): Negative for real images, positive for virtual images.
- Focal length (f): Always negative.
- Radius of curvature (R): Negative.
- Height above principal axis: Positive; below: negative.
8. Can you explain the sign convention for object and image distances in a convex lens?
In a convex lens, the following sign convention applies for object and image distances:
- Object distance (u): Always negative (object placed to the left of lens).
- Image distance (v): Positive if image forms on opposite side of lens (real and inverted), negative if on same side as object (virtual and erect).
- Focal length (f): Positive.
9. What is the general sign convention applied in optics?
The general sign convention in optics is known as the Cartesian Sign Convention:
- All distances are measured from the optical centre or pole.
- Left of the origin (against incident light): Negative distances.
- Right of the origin (along incident light): Positive distances.
- Heights above axis: Positive; below: negative.
- Focal length’s sign depends on lens/mirror type as per standard rules.
10. Define the lens formula and state how sign convention is used in it.
The lens formula relates the object distance (u), image distance (v), and focal length (f):
- Lens Formula: 1/v - 1/u = 1/f
- Assign negative or positive signs to u, v, f based on the New Cartesian Sign Convention.
- Always measure from the optical centre.
- Focal length is positive for convex, negative for concave lenses.
- Correct sign assignment is essential for accurate answers in exams.
























