




Key Features and Formula of a Plane Progressive Harmonic Wave
The equation of a plane progressive harmonic wave is a core concept in wave physics and is essential for understanding how disturbances propagate through a medium. This equation describes the displacement of particles in a medium as the wave travels, highlighting the relationship between amplitude, frequency, wavelength, and phase.
Fundamental Properties of Plane Progressive Harmonic Waves
A plane progressive harmonic wave is characterized by constant amplitude and frequency as it moves in a fixed direction without changing its form. The displacement of each particle follows simple harmonic motion as the wave propagates. For detailed study of simple harmonic motion, refer to Simple Harmonic Motion.
Mathematical Representation of Simple Harmonic Motion
The displacement of a particle in simple harmonic motion is given by $y = A \sin \omega t$, where $A$ is amplitude and $\omega$ is angular frequency. For a particle at position $x$ along the direction of propagation, the phase depends on its distance from the origin.
Derivation of the Plane Progressive Harmonic Wave Equation
Consider a plane progressive harmonic wave traveling along the positive $x$-axis. The displacement $y$ of a particle at position $x$ and time $t$ is influenced by both time and space variables. The phase difference between two positions separated by distance $x$ is proportional to $\dfrac{2\pi x}{\lambda}$, where $\lambda$ is the wavelength.
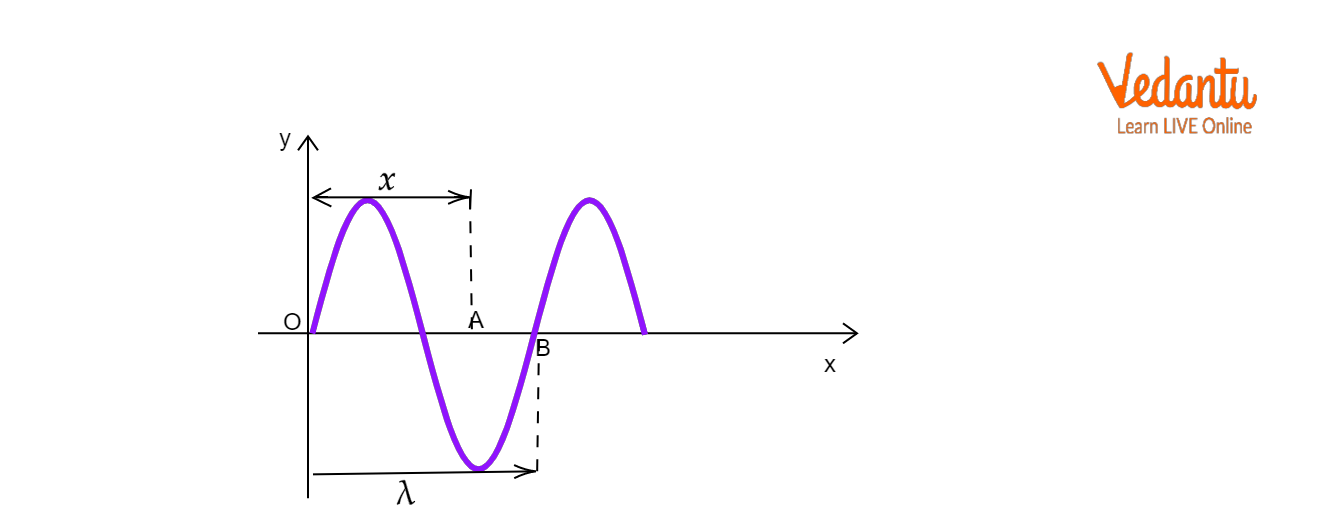
Using these parameters, the equation for the displacement becomes:
$y = A \sin(\omega t - \dfrac{2\pi x}{\lambda})$
Here, $A$ is amplitude, $\omega$ is angular frequency, $t$ is time, $x$ is position, and $\lambda$ is wavelength. The term $\omega t - \dfrac{2\pi x}{\lambda}$ represents the phase of the wave at a particular point and time.
Alternative Forms of the Progressive Wave Equation
The wave equation can also be expressed using frequency $f$ and time period $T$, where $\omega = 2\pi f$ and $T = 1/f$. Substituting these in, other standard forms are:
$y = A \sin\left[2\pi \left(ft - \dfrac{x}{\lambda}\right)\right]$
$y = A \sin\left[\dfrac{2\pi t}{T} - \dfrac{2\pi x}{\lambda}\right]$
Physical Parameters of a Plane Progressive Harmonic Wave
Key physical properties are amplitude, wavelength, frequency, time period, and wave speed. These parameters define the shape and motion of the wave. For comprehensive study on relationships among these properties, see Frequency And Wavelength Relationship.
Explanation of Each Term in the Wave Equation
| Symbol | Physical Meaning |
|---|---|
| $A$ | Amplitude (maximum displacement) |
| $\omega$ | Angular frequency ($2\pi f$) |
| $t$ | Time variable |
| $x$ | Position along propagation |
| $\lambda$ | Wavelength of the wave |
Characteristics of Plane Progressive Harmonic Waves
- All particles undergo simple harmonic motion
- The amplitude remains constant over time
- The frequency is the same for all particles
- The wave propagates energy along its direction
- The waveform maintains its shape during propagation
Wave Speed and Related Expressions
The speed $v$ of a plane progressive harmonic wave is given by $v = \dfrac{\lambda}{T} = \lambda f$. This indicates that wave speed depends on both wavelength and frequency. For foundational understanding of wave motion, visit Wave Motion.
Example: Equation for a Specific Progressive Wave
For a wave of amplitude $0.01$ m, frequency $100$ Hz, speed $50$ m/s and propagating in the positive $x$-direction, the wavelength is $\lambda = \dfrac{v}{f} = 0.5$ m. Substituting these values into the equation:
$y = 0.01 \sin \left[2\pi (100 t) - \dfrac{2\pi x}{0.5}\right]$
Difference Between Progressive and Standing Waves
A progressive wave continuously transfers energy and moves forward, whereas a standing wave does not transfer energy in the direction of propagation and forms fixed nodes and antinodes. The mathematical forms of these waves are distinct. Further information on wave types is available at Longitudinal And Transverse Waves.
Key Points on Plane Progressive Harmonic Wave Equations
- Describes displacement as a function of $x$ and $t$
- Applies to mechanical and electromagnetic waves
- Fundamental in sound, light, and other wave phenomena
An in-depth grasp of the plane progressive harmonic wave equation is vital for mastering further topics in waves and oscillations. For advanced study and related concepts, see Oscillations And Waves and Wave Particle Duality.
FAQs on Understanding the Plane Progressive Harmonic Wave Equation
1. What is the equation of a plane progressive harmonic wave?
The equation of a plane progressive harmonic wave describes the displacement of particles as the wave travels in a single direction with a constant amplitude and frequency. It is generally written as:
y(x, t) = A sin(kx – ωt + φ), where:
- y(x, t) = displacement at position x and time t
- A = amplitude of the wave
- k = wave number (2π/λ), where λ is the wavelength
- ω = angular frequency (2πv), where v is frequency
- φ = initial phase of the wave
2. What are the characteristics of a plane progressive harmonic wave?
A plane progressive harmonic wave has distinct properties that define its motion and structure:
- Travels in a fixed direction without changing shape or amplitude
- All particles move in simple harmonic motion with the same amplitude
- Constant velocity of propagation
- Wavelength and frequency remain unchanged
- Energy is transferred continuously but not the medium itself
3. What is the difference between a progressive wave and a stationary wave?
Progressive waves and stationary waves differ mainly in their motion and energy transfer:
- Progressive wave: Energy travels forward; all particles vibrate with same amplitude but with progressive phase difference.
- Stationary wave: Results from the superposition of two progressive waves of same frequency moving in opposite directions; energy does not travel, and nodes and antinodes are formed.
4. How do you calculate the velocity of a plane progressive wave?
The velocity (v) of a plane progressive harmonic wave can be calculated using:
- v = ω / k, where ω is the angular frequency and k is the wave number
- Alternatively, v = f × λ, where f is the frequency and λ is the wavelength
5. State the mathematical form of a plane progressive harmonic wave travelling along the positive x-axis.
A plane progressive harmonic wave traveling in the positive x-direction is given by:
y(x, t) = A sin(kx – ωt + φ),
where all variables have their standard meanings. The sign before ωt indicates the direction of propagation.
6. What do amplitude, wavelength, and phase mean in the wave equation?
Amplitude (A), Wavelength (λ), and Phase (φ) are key parameters:
- Amplitude: Maximum displacement from mean position
- Wavelength: Distance between two consecutive points in phase (e.g., two crests)
- Phase: Specifies the initial angle and relative position of oscillation
7. What do you mean by the term 'wave number' and 'angular frequency'?
Wave number (k) and angular frequency (ω) are essential wave parameters:
- Wave number (k): 2π divided by wavelength (k = 2π/λ); represents the number of waves per unit distance
- Angular frequency (ω): 2π times the frequency (ω = 2πf); describes how quickly the wave oscillates in radians per second
8. How is energy transmitted in a plane progressive wave?
In a plane progressive harmonic wave, energy is transmitted through the medium as each particle oscillates about its mean position, passing energy to its neighbors. No matter is transported, only energy:
- Particles vibrate simple harmonically
- Energy flows continuously from source to receiver
- The medium itself does not move with the wave
9. What are the conditions for the formation of a plane progressive wave?
For a plane progressive harmonic wave to form, the following conditions should be met:
- The medium must be elastic and homogeneous
- The source should vibrate with constant frequency and amplitude
- No significant energy loss during propagation
- Wave travels unidirectionally without distortion
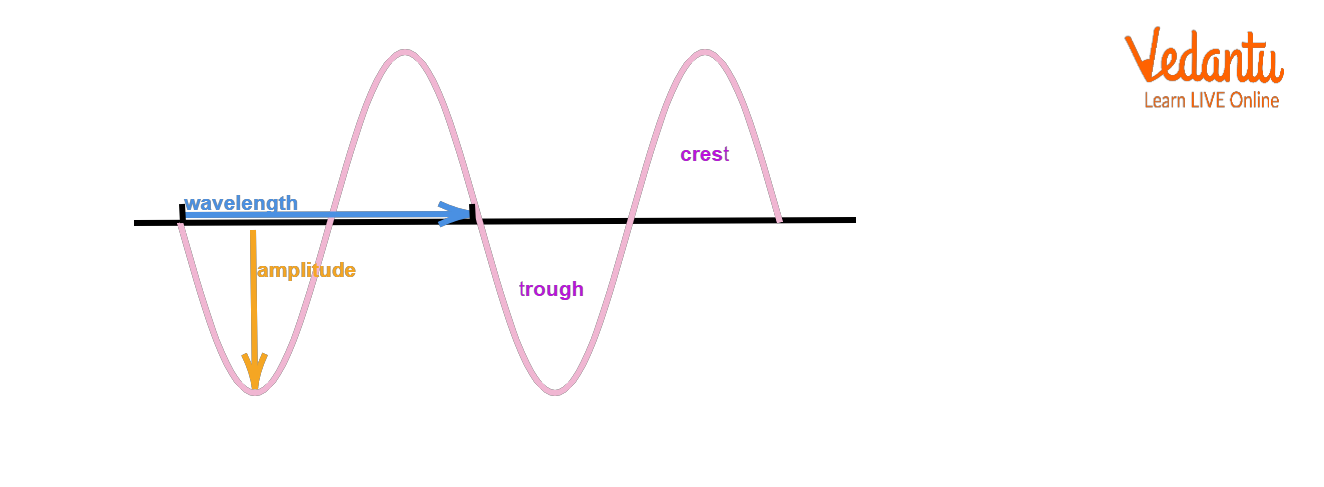
10. Explain the terms crest, trough, and node in relation to plane progressive waves.
Crest, trough, and node are points of significance in wave motion:
- Crest: The highest point of a wave above mean position
- Trough: The lowest point below mean position
- Node: A point where displacement is always zero (mostly in stationary waves, but useful for comparison)
























