




Key Differences Between Parallel and Mixed Cell Groupings
Parallel and mixed grouping of cells are essential concepts in current electricity, widely applied in both theory and numerical problems. Understanding their principles allows for efficient arrangement of cells to achieve required voltage and current in practical and examination settings.
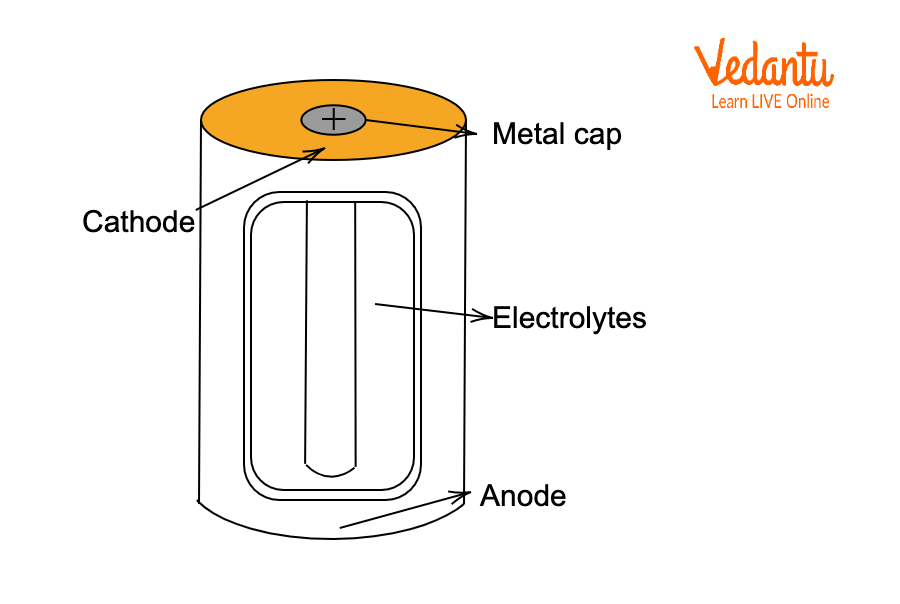
Definitions and Key Principles of Grouping Cells
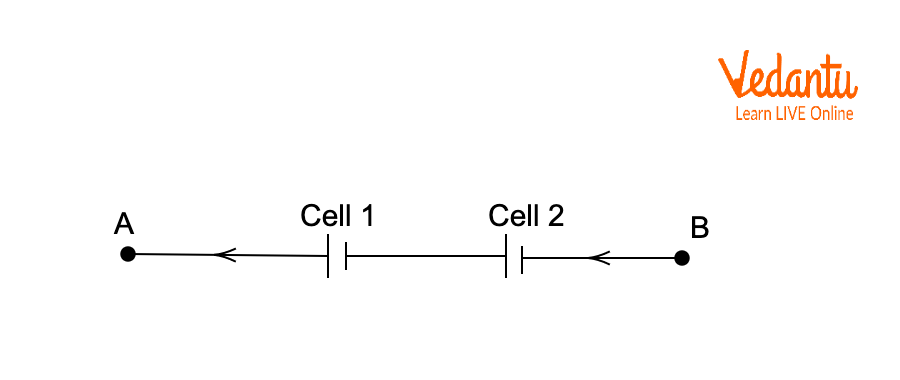
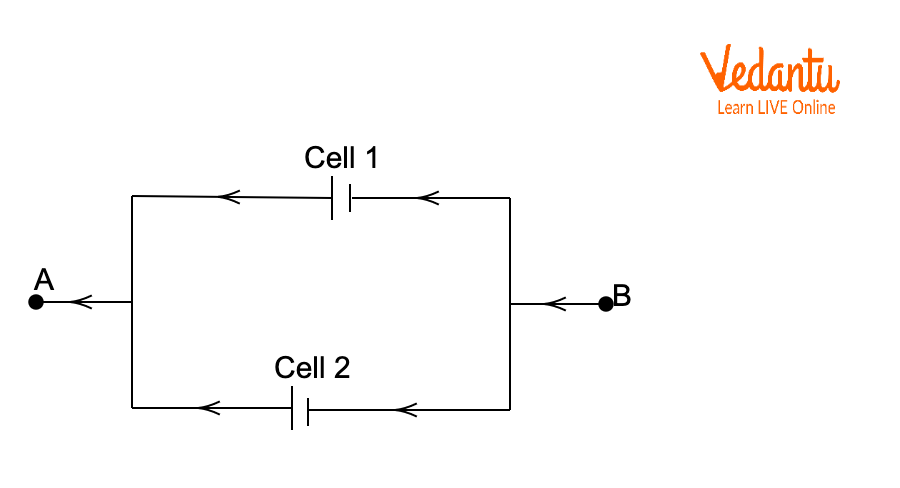
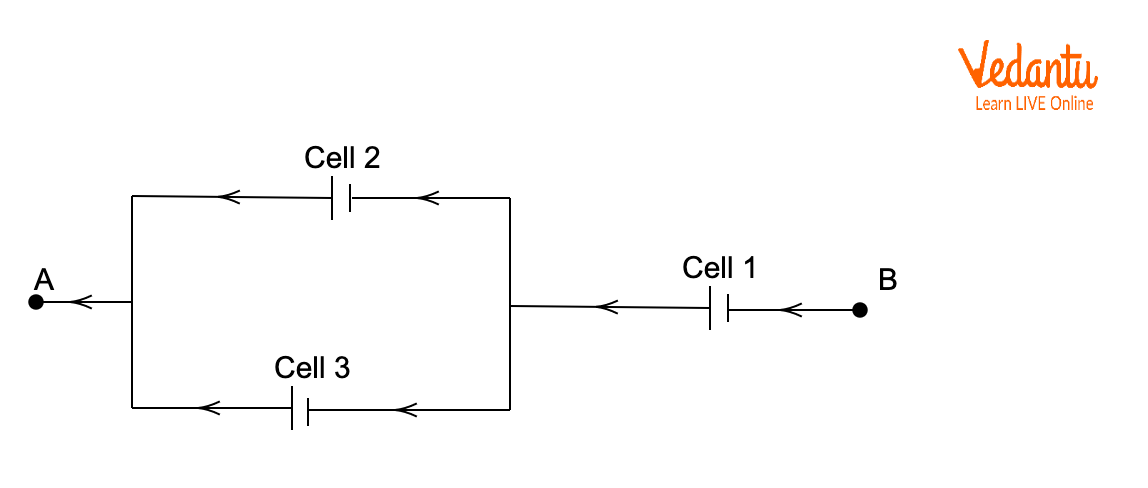
Cells can be arranged in series, in parallel, or combined as mixed grouping, each yielding specific outcomes for total emf and internal resistance. Series grouping increases voltage, parallel grouping enhances current capacity, and mixed grouping adjusts both quantities as required.
Series, Parallel, and Mixed Grouping: Circuit Diagrams
In series grouping, the positive terminal of one cell connects to the negative terminal of the next, resulting in cumulative voltages. In parallel grouping, all positive terminals and all negative terminals are joined, maintaining voltage but increasing current supply. Mixed grouping combines these arrangements.
Mathematical Analysis of Cell Combinations
For $n$ identical cells of emf $\varepsilon$ and internal resistance $r$, key formulas differ according to arrangement. Series combination gives highest voltage; parallel gives higher current; mixed grouping achieves tailored output.
| Arrangement | Total EMF ($E_\text{eq}$) and Total Internal Resistance ($r_\text{eq}$) |
|---|---|
| Series ($n$ cells) | $n\varepsilon$, $nr$ |
| Parallel ($m$ cells) | $\varepsilon$, $r/m$ |
| Mixed ($n$ in series, $m$ parallel branches) | $n\varepsilon$, $nr/m$ |
For non-identical cells in parallel, the equivalent emf is obtained by $E_\text{eq} = \dfrac{\sum \left(\dfrac{E_i}{r_i}\right)}{\sum \left(\dfrac{1}{r_i}\right)}$, considering individual emfs and internal resistances. Correct formula selection is critical for accurate calculations in competitive exams.
Cell combination analysis closely relates to concepts covered in Series And Parallel Combination Of Springs for students comparing different electrical systems.
Practical Applications of Cell Grouping
Series arrangements appear in torches and remotes where higher voltage is required. Parallel groupings are chosen in power banks and battery arrays for increased current capability. Mixed grouping finds use in high-power devices such as inverters and industrial equipment.
- Series: Useful in devices needing high voltage
- Parallel: Applied where high current is necessary
- Mixed: Provides flexible voltage and current control
Understanding cell grouping principles is vital for Electric Circuit Overview and circuit optimization problems.
Example: Mixed Grouping Calculation in JEE Main
Consider $n$ cells (each emf $\varepsilon$, internal resistance $r$) in series, and $m$ such series groups connected in parallel to a load resistance $R$. The total emf is $n\varepsilon$ and effective internal resistance $nr/m$.
The current through load $R$ is $I = \dfrac{n\varepsilon}{R + \dfrac{nr}{m}}$.
Selection between series, parallel and mixed grouping directly affects output voltage and current, similar to distinctions discussed in Difference Between Series And Parallel Circuits.
Key Differences and Optimal Uses
Series grouping increases output voltage, while parallel enhances current without increasing voltage. Mixed grouping allows both voltage and current adjustment for circuit requirements. Choice depends on the desired application and circuit limitations.
| Use Case | Best Grouping |
|---|---|
| High voltage requirement | Series |
| High current with constant voltage | Parallel |
| Both high voltage and current | Mixed |
For further study on how groupings affect resistance, refer to Difference Between Resistance And Resistivity for conceptual comparison.
Important Considerations and Common Mistakes
Cells combined in parallel must have equal emf to prevent reverse current that can reduce efficiency and damage cells. Internal resistances must always be considered for reliable calculations, especially in examination settings.
- Do not add emf values directly in parallel grouping
- Always include internal resistance in mixed arrangements
- Use identical cells for parallel grouping to avoid current loss
- Label all diagrams clearly in answer scripts
Accurate application of these rules is essential in both board examination and competitive problem solving, ensuring correct solution to grouping questions.
Mixed cell grouping analysis also supports deeper understanding for topics like Cells In Series And Parallel and advanced circuits analysis.
Related Analytical Approaches
Application of Kirchhoff’s Laws is recommended for analysing circuits with complex grouping. Techniques similar to those in RC Circuit Analysis can be adapted for solving advanced current electricity questions involving combination of cells.
FAQs on Understanding Parallel and Mixed Grouping of Cells
1. What is meant by parallel grouping of cells?
Parallel grouping of cells means connecting all the positive terminals together and all the negative terminals together, allowing the battery to supply the same voltage as a single cell, but with increased current capacity.
Key points:
- All cells are connected so positive terminals join, and negative terminals join.
- Total voltage across the arrangement is equal to the voltage of one cell.
- Total current supplied is the sum of current from each cell.
- Helps in increasing battery life and can power devices needing high current.
2. What is mixed grouping of cells?
Mixed grouping of cells is a combination of both series and parallel groupings, used to achieve desired values of current and voltage.
Important features:
- Cells are arranged in several parallel rows (parallel grouping), and then these are connected together in series.
- This method balances both the required voltage and current.
- Used when neither pure series nor pure parallel grouping alone meets circuit demands.
3. What is the difference between series, parallel, and mixed grouping of cells?
Series grouping increases voltage, parallel grouping increases current, and mixed grouping provides both increased voltage and current as required.
Comparison:
- Series: Voltage adds, current stays same; used for high voltage requirements.
- Parallel: Voltage stays same, current adds up; used for high current requirements.
- Mixed: Combines both; used when both high voltage and current are needed.
4. What are the advantages of connecting cells in parallel?
Parallel grouping of cells has several advantages, especially when high current is needed.
- Battery lasts longer as the current is shared by multiple cells.
- If one cell fails, others keep working and device continues running.
- Same voltage is available as a single cell, suitable for electronics that need stable voltage.
- Heat generation is reduced as current is divided.
5. In which situations is mixed grouping of cells used?
Mixed grouping of cells is used when a device requires both higher voltage and increased current.
- Applied in heavy electrical circuits and scientific experiments.
- Used in battery packs for electric vehicles to match voltage and current demands.
- Essential when neither only more voltage (series) nor only more current (parallel) is sufficient.
6. How does connecting cells in parallel affect the total voltage and current supplied?
Connecting cells in parallel keeps the overall voltage equal to a single cell's voltage, while the total current capacity is the sum of the individual cell currents.
- Voltage = one cell's voltage.
- Total current = sum of all cell currents.
- Useful for devices that require larger currents at low voltage.
7. What precautions should be taken while connecting cells in parallel or mixed grouping?
When connecting cells in parallel or mixed grouping, it is important to follow safety guidelines for efficient functioning.
- Use cells with the same voltage and capacity to avoid malfunction.
- Check polarity: connect positive to positive and negative to negative for parallel, and alternate for series within mixed grouping.
- Make secure, clean connections to minimize resistance.
- Avoid overloading the battery pack to prevent overheating and damage.
8. What is the formula for calculating the total current and voltage in mixed grouping of cells?
In mixed grouping (n rows each with m cells in series):
- Total voltage = m × voltage of one cell
- Total current = n × current supplied by one row
- Mixed grouping provides flexibility to match voltages and currents as per requirement.
9. Why is internal resistance important in the grouping of cells?
The internal resistance of cells affects the overall efficiency of a battery arrangement.
- High internal resistance decreases the effective voltage and current output.
- In parallel grouping, overall internal resistance decreases, making it more efficient for high current devices.
- In series grouping, resistance increases, which can lower efficiency if not managed.
10. What happens if cells of unequal EMF are connected in parallel?
When cells with unequal EMF are connected in parallel, it can cause circulating currents between the cells, leading to energy loss, overheating, or damage.
- Always use cells of same EMF in parallel configurations.
- Different EMFs can waste power and reduce the battery life.























